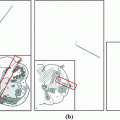
computed tomography (CT) images of the lumbar spine. The overall segmentation performance of  mm in terms of mean symmetric absolute surface distance and
mm in terms of mean symmetric absolute surface distance and  in terms of Dice coefficient, computed against corresponding reference vertebra segmentations, indicates that the proposed framework can accurately segment vertebrae from CT images of the lumbar spine.
in terms of Dice coefficient, computed against corresponding reference vertebra segmentations, indicates that the proposed framework can accurately segment vertebrae from CT images of the lumbar spine.
1 Introduction
Accurate and robust segmentation of spinal and vertebral structures from medical images is a challenging task due to a relatively high degree of anatomical complexity (i.e. vertebrae consisting of the vertebral body, pedicles, laminae and spinous process) and due to the articulation of vertebrae with each other. In addition to the complexity and articulation, the problem also lies in insufficient image spatial resolution, inhomogeneity and low signal-to-noise ratio. Since skeletal structures have high contrast when observed in computed tomography (CT) images, CT is commonly the modality of choice for assessing three-dimensional (3D) skeletal structures, such as the spine and vertebrae.
In recent years, several automated and semi-automated methods focusing on the vertebra segmentation problem have been developed for CT images. Kim and Kim [8] proposed a fully automated method that constructs 3D fences to separate vertebrae from valley-emphasized Gaussian images, and then the region growing algorithm is applied within 3D fences to obtain the final segmentation. Klinder et al. [9] progressively adapted tube-shaped segments to extract the spine curve, performed vertebra detection on curved-planar reformatted images using the generalized Hough transform, identified vertebrae by rigid registration of appearance models to the detected candidates, and obtained the final segmentation by adapting shape-constrained models of the individual vertebrae. Kadoury et al. [6, 7] built an articulated shape manifold from a training database by embedding the data into a low-dimensional sub-space, and applied the Markov random field optimization to infer between the unseen target shape and shape manifold. Lim et al. [10] incorporated local geometrical features using the Willmore flow and prior shape knowledge by kernel density estimation into a level set segmentation framework. Ma and Lu [12] introduced a learning-based bone structure edge detection algorithm and hierarchical coarse-to-fine deformable surface-based segmentation that relied on response maps of a trained edge detector. Rasoulian et al. [14] developed a statistical multi-vertebrae model of shape and pose, and proposed a novel iterative expectation maximization registration technique to align the model to CT images of the spine. Ibragimov et al. [5] presented a segmentation framework, in which a novel landmark-based shape representation of vertebrae was combined with a landmark detection framework based on game theory.
In this paper, we describe an improved framework for vertebra segmentation that is based on the shape-constrained deformable model [9, 15]. Our framework is initialized by the results of a novel vertebra detection and alignment algorithm [4], and the segmentation of each vertebra is then obtained by a mesh deformation technique that moves mesh vertices to their optimal locations while preserving the underlying vertebral shape. The performance of the proposed segmentation framework was evaluated on vertebrae from CT images of the lumbar spine, and the obtained results with the mean error below  mm indicate that accurate segmentation of vertebrae was achieved.
mm indicate that accurate segmentation of vertebrae was achieved.
 mm indicate that accurate segmentation of vertebrae was achieved.
mm indicate that accurate segmentation of vertebrae was achieved.2 Methodology
2.1 Mean Shape Model of the Lumbar Spine
Let set 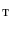 contain 3D images of the lumbar spine, where each image is assigned a series of binary masks representing reference segmentations of each individual lumbar vertebra from level L1 to L5. To extract a shape model of each vertebra from each image in
contain 3D images of the lumbar spine, where each image is assigned a series of binary masks representing reference segmentations of each individual lumbar vertebra from level L1 to L5. To extract a shape model of each vertebra from each image in  , the marching cubes algorithm [11] is applied to each corresponding binary mask, resulting in a 3D face-vertex mesh consisting of vertices with triangle connectivity information. The dependency of the number of vertices in each mesh on the size of the image voxel and of the observed vertebra is removed by isotropic remeshing [1]. In order to establish pointwise correspondences among vertices of the same vertebral level, the nonrigid transformation among sets of vertices is recovered using state-of-the-art coherent point drift algorithm [13] that outperforms other methods for point set registration. Finally, the generalized Procrustes alignment [3] is used to remove translation, rotation and scaling from corresponding meshes, yielding the mean shape model of each vertebra, represented by a 3D face-vertex mesh
, the marching cubes algorithm [11] is applied to each corresponding binary mask, resulting in a 3D face-vertex mesh consisting of vertices with triangle connectivity information. The dependency of the number of vertices in each mesh on the size of the image voxel and of the observed vertebra is removed by isotropic remeshing [1]. In order to establish pointwise correspondences among vertices of the same vertebral level, the nonrigid transformation among sets of vertices is recovered using state-of-the-art coherent point drift algorithm [13] that outperforms other methods for point set registration. Finally, the generalized Procrustes alignment [3] is used to remove translation, rotation and scaling from corresponding meshes, yielding the mean shape model of each vertebra, represented by a 3D face-vertex mesh  of
of 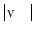 vertices and
vertices and  faces (i.e. triangles). The mean shape model of the whole lumbar spine, i.e. a chain of mean shape models of individual vertebrae, is further used for spine detection, while the mean shape models of individual vertebrae are used for vertebra detection and segmentation in an unknown 3D image
faces (i.e. triangles). The mean shape model of the whole lumbar spine, i.e. a chain of mean shape models of individual vertebrae, is further used for spine detection, while the mean shape models of individual vertebrae are used for vertebra detection and segmentation in an unknown 3D image  .
.
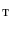 contain 3D images of the lumbar spine, where each image is assigned a series of binary masks representing reference segmentations of each individual lumbar vertebra from level L1 to L5. To extract a shape model of each vertebra from each image in
contain 3D images of the lumbar spine, where each image is assigned a series of binary masks representing reference segmentations of each individual lumbar vertebra from level L1 to L5. To extract a shape model of each vertebra from each image in  , the marching cubes algorithm [11] is applied to each corresponding binary mask, resulting in a 3D face-vertex mesh consisting of vertices with triangle connectivity information. The dependency of the number of vertices in each mesh on the size of the image voxel and of the observed vertebra is removed by isotropic remeshing [1]. In order to establish pointwise correspondences among vertices of the same vertebral level, the nonrigid transformation among sets of vertices is recovered using state-of-the-art coherent point drift algorithm [13] that outperforms other methods for point set registration. Finally, the generalized Procrustes alignment [3] is used to remove translation, rotation and scaling from corresponding meshes, yielding the mean shape model of each vertebra, represented by a 3D face-vertex mesh
, the marching cubes algorithm [11] is applied to each corresponding binary mask, resulting in a 3D face-vertex mesh consisting of vertices with triangle connectivity information. The dependency of the number of vertices in each mesh on the size of the image voxel and of the observed vertebra is removed by isotropic remeshing [1]. In order to establish pointwise correspondences among vertices of the same vertebral level, the nonrigid transformation among sets of vertices is recovered using state-of-the-art coherent point drift algorithm [13] that outperforms other methods for point set registration. Finally, the generalized Procrustes alignment [3] is used to remove translation, rotation and scaling from corresponding meshes, yielding the mean shape model of each vertebra, represented by a 3D face-vertex mesh  of
of 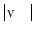 vertices and
vertices and  faces (i.e. triangles). The mean shape model of the whole lumbar spine, i.e. a chain of mean shape models of individual vertebrae, is further used for spine detection, while the mean shape models of individual vertebrae are used for vertebra detection and segmentation in an unknown 3D image
faces (i.e. triangles). The mean shape model of the whole lumbar spine, i.e. a chain of mean shape models of individual vertebrae, is further used for spine detection, while the mean shape models of individual vertebrae are used for vertebra detection and segmentation in an unknown 3D image  .
.2.2 Vertebra Detection
The detection of vertebrae in an unknown 3D image 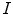 was performed by a novel optimization scheme that is based on interpolation theory [4]. The optimization scheme consists of three steps: spine detection, vertebra detection and vertebra alignment. To detect the spine in image
was performed by a novel optimization scheme that is based on interpolation theory [4]. The optimization scheme consists of three steps: spine detection, vertebra detection and vertebra alignment. To detect the spine in image 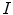 , the pose of mesh
, the pose of mesh 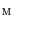 representing the mean shape model of the lumbar spine (i.e. a chain of meshes representing individual vertebrae from L1 to L5) is optimized against three translations (i.e. coordinates
representing the mean shape model of the lumbar spine (i.e. a chain of meshes representing individual vertebrae from L1 to L5) is optimized against three translations (i.e. coordinates  ,
,  and
and  representing sagittal, coronal and axial anatomical directions, respectively). The global maximum of the resulting interpolation represents the location of the spine in the 3D image, and is further used to initialize the detection of individual vertebrae. To detect individual vertebrae, the pose of mesh
representing sagittal, coronal and axial anatomical directions, respectively). The global maximum of the resulting interpolation represents the location of the spine in the 3D image, and is further used to initialize the detection of individual vertebrae. To detect individual vertebrae, the pose of mesh  , now representing the mean shape model of the observed lumbar vertebra, is optimized against three translations, however, in this case all local maxima of the resulting interpolation are extracted, corresponding to locations of the observed and neighboring vertebrae. The correct location of each vertebra is determined by the optimal path that passes through a set of locations, where each location belongs to a local maxima at a different vertebral level. Finally, a more accurate alignment of the mean shape model of each observed vertebra is performed by optimizing the pose of each model against three translations, one scaling (i.e. factor
, now representing the mean shape model of the observed lumbar vertebra, is optimized against three translations, however, in this case all local maxima of the resulting interpolation are extracted, corresponding to locations of the observed and neighboring vertebrae. The correct location of each vertebra is determined by the optimal path that passes through a set of locations, where each location belongs to a local maxima at a different vertebral level. Finally, a more accurate alignment of the mean shape model of each observed vertebra is performed by optimizing the pose of each model against three translations, one scaling (i.e. factor  ) and three rotations (i.e. angles
) and three rotations (i.e. angles  ,
, 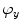 and
and 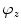 about coordinate axes
about coordinate axes 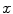 ,
,  and
and  , respectively). The resulting alignment represents the final vertebra detection result. A detailed description of the interpolation-based optimization scheme can be found in [4].
, respectively). The resulting alignment represents the final vertebra detection result. A detailed description of the interpolation-based optimization scheme can be found in [4].
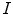 was performed by a novel optimization scheme that is based on interpolation theory [4]. The optimization scheme consists of three steps: spine detection, vertebra detection and vertebra alignment. To detect the spine in image
was performed by a novel optimization scheme that is based on interpolation theory [4]. The optimization scheme consists of three steps: spine detection, vertebra detection and vertebra alignment. To detect the spine in image 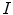 , the pose of mesh
, the pose of mesh 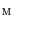 representing the mean shape model of the lumbar spine (i.e. a chain of meshes representing individual vertebrae from L1 to L5) is optimized against three translations (i.e. coordinates
representing the mean shape model of the lumbar spine (i.e. a chain of meshes representing individual vertebrae from L1 to L5) is optimized against three translations (i.e. coordinates  ,
,  and
and  representing sagittal, coronal and axial anatomical directions, respectively). The global maximum of the resulting interpolation represents the location of the spine in the 3D image, and is further used to initialize the detection of individual vertebrae. To detect individual vertebrae, the pose of mesh
representing sagittal, coronal and axial anatomical directions, respectively). The global maximum of the resulting interpolation represents the location of the spine in the 3D image, and is further used to initialize the detection of individual vertebrae. To detect individual vertebrae, the pose of mesh  , now representing the mean shape model of the observed lumbar vertebra, is optimized against three translations, however, in this case all local maxima of the resulting interpolation are extracted, corresponding to locations of the observed and neighboring vertebrae. The correct location of each vertebra is determined by the optimal path that passes through a set of locations, where each location belongs to a local maxima at a different vertebral level. Finally, a more accurate alignment of the mean shape model of each observed vertebra is performed by optimizing the pose of each model against three translations, one scaling (i.e. factor
, now representing the mean shape model of the observed lumbar vertebra, is optimized against three translations, however, in this case all local maxima of the resulting interpolation are extracted, corresponding to locations of the observed and neighboring vertebrae. The correct location of each vertebra is determined by the optimal path that passes through a set of locations, where each location belongs to a local maxima at a different vertebral level. Finally, a more accurate alignment of the mean shape model of each observed vertebra is performed by optimizing the pose of each model against three translations, one scaling (i.e. factor  ) and three rotations (i.e. angles
) and three rotations (i.e. angles  ,
, 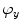 and
and 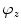 about coordinate axes
about coordinate axes 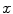 ,
,  and
and  , respectively). The resulting alignment represents the final vertebra detection result. A detailed description of the interpolation-based optimization scheme can be found in [4].
, respectively). The resulting alignment represents the final vertebra detection result. A detailed description of the interpolation-based optimization scheme can be found in [4].2.3 Vertebra Segmentation
After the interpolation-based alignment [4] of the mean shape model of each lumbar vertebra to the unknown image  , segmentation of each lumbar vertebra is performed by a mesh deformation technique that moves mesh vertices to their optimal locations while preserving the underlying vertebral shape [9, 15]. In this iterative procedure, the following two steps are executed in each iteration: image object detection for mesh face centroids that are represented by the centers of mass for mesh faces
, segmentation of each lumbar vertebra is performed by a mesh deformation technique that moves mesh vertices to their optimal locations while preserving the underlying vertebral shape [9, 15]. In this iterative procedure, the following two steps are executed in each iteration: image object detection for mesh face centroids that are represented by the centers of mass for mesh faces  , followed by reconfiguration of mesh vertices
, followed by reconfiguration of mesh vertices  . By combining the robust initialization resulting from vertebra detection (Sect. 2.2) with modifications to the mesh deformation technique, we improve the accuracy of the resulting vertebra segmentation.
. By combining the robust initialization resulting from vertebra detection (Sect. 2.2) with modifications to the mesh deformation technique, we improve the accuracy of the resulting vertebra segmentation.
 , segmentation of each lumbar vertebra is performed by a mesh deformation technique that moves mesh vertices to their optimal locations while preserving the underlying vertebral shape [9, 15]. In this iterative procedure, the following two steps are executed in each iteration: image object detection for mesh face centroids that are represented by the centers of mass for mesh faces
, segmentation of each lumbar vertebra is performed by a mesh deformation technique that moves mesh vertices to their optimal locations while preserving the underlying vertebral shape [9, 15]. In this iterative procedure, the following two steps are executed in each iteration: image object detection for mesh face centroids that are represented by the centers of mass for mesh faces  , followed by reconfiguration of mesh vertices
, followed by reconfiguration of mesh vertices  . By combining the robust initialization resulting from vertebra detection (Sect. 2.2) with modifications to the mesh deformation technique, we improve the accuracy of the resulting vertebra segmentation.
. By combining the robust initialization resulting from vertebra detection (Sect. 2.2) with modifications to the mesh deformation technique, we improve the accuracy of the resulting vertebra segmentation.2.3.1 Object Detection
By displacing each mesh face centroid  ;
; 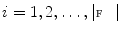 along its corresponding mesh face normal
along its corresponding mesh face normal 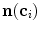 , a new candidate mesh face centroid
, a new candidate mesh face centroid  is found in each
is found in each  th iteration:
th iteration:
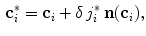
where  is the length of the unit displacement, and
is the length of the unit displacement, and  is an element from set
is an element from set  ;
; 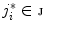 . Set
. Set 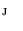 represents the search profile along
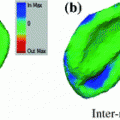
represents the search profile along  , called the sampling parcel (Fig.1):
, called the sampling parcel (Fig.1):
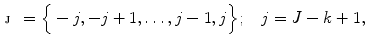
which is of size  at initial iteration
at initial iteration 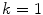 and
and  at final iteration
at final iteration 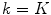 . The element
. The element 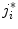 that defines the location of
that defines the location of  is determined by detecting vertebra boundaries:
is determined by detecting vertebra boundaries:
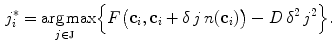
where 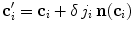 is the candidate location for
is the candidate location for  (Eq. 1), and parameter
(Eq. 1), and parameter 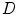 controls the tradeoff between the response of the boundary detection operator
controls the tradeoff between the response of the boundary detection operator  (Eq. 4) and the distance from
(Eq. 4) and the distance from 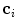 to
to  . In comparison to the original approach [9, 15], we propose an improved boundary detection operator
. In comparison to the original approach [9, 15], we propose an improved boundary detection operator  that is based on image intensity gradients, weighted by an image appearance operator:
that is based on image intensity gradients, weighted by an image appearance operator:
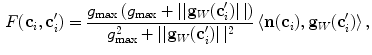
where 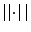 denotes the vector norm,
denotes the vector norm, 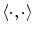 denotes the dot product,
denotes the dot product, 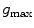 is the estimated mean amplitude of intensity gradients at vertebra boundaries that is used to suppresses the weighted gradients, which may occur if the gradient magnitude at the boundary of the object of interest is considerably smaller than of another object in its neighborhood (e.g. pedicle screws), and
is the estimated mean amplitude of intensity gradients at vertebra boundaries that is used to suppresses the weighted gradients, which may occur if the gradient magnitude at the boundary of the object of interest is considerably smaller than of another object in its neighborhood (e.g. pedicle screws), and  is the image appearance operator at candidate mesh centroid location
is the image appearance operator at candidate mesh centroid location 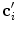 :
:
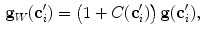
where  is the intensity gradient at
is the intensity gradient at 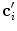 and
and ![$$C(\mathbf {c}_i') \in [0,1]$$](/wp-content/uploads/2016/10/A331518_1_En_8_Chapter_IEq59.gif) is the continuous response to the Canny edge operator [2]. By adding additional weights to the image intensity gradients, vertebra boundary points are more likely to be detected. In contrast to the original technique [9, 15], the size of the sampling parcel
is the continuous response to the Canny edge operator [2]. By adding additional weights to the image intensity gradients, vertebra boundary points are more likely to be detected. In contrast to the original technique [9, 15], the size of the sampling parcel  (Eq. 2) is reduced in each iteration
(Eq. 2) is reduced in each iteration  and the image intensity gradients
and the image intensity gradients  (Eq. 5) are additionally weighted, both to improve the accuracy of the resulting segmentation.
(Eq. 5) are additionally weighted, both to improve the accuracy of the resulting segmentation.
 ;
; 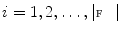 along its corresponding mesh face normal
along its corresponding mesh face normal 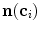 , a new candidate mesh face centroid
, a new candidate mesh face centroid  is found in each
is found in each  th iteration:
th iteration: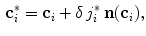
(1)
 is the length of the unit displacement, and
is the length of the unit displacement, and  is an element from set
is an element from set  ;
; 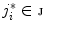 . Set
. Set 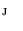 represents the search profile along
represents the search profile along  , called the sampling parcel (Fig.1):
, called the sampling parcel (Fig.1):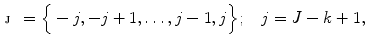
(2)
 at initial iteration
at initial iteration 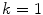 and
and  at final iteration
at final iteration 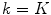 . The element
. The element 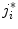 that defines the location of
that defines the location of  is determined by detecting vertebra boundaries:
is determined by detecting vertebra boundaries: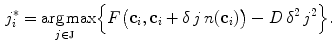
(3)
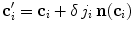 is the candidate location for
is the candidate location for  (Eq. 1), and parameter
(Eq. 1), and parameter 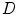 controls the tradeoff between the response of the boundary detection operator
controls the tradeoff between the response of the boundary detection operator  (Eq. 4) and the distance from
(Eq. 4) and the distance from 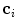 to
to  . In comparison to the original approach [9, 15], we propose an improved boundary detection operator
. In comparison to the original approach [9, 15], we propose an improved boundary detection operator  that is based on image intensity gradients, weighted by an image appearance operator:
that is based on image intensity gradients, weighted by an image appearance operator: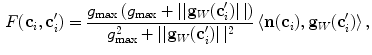
(4)
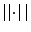 denotes the vector norm,
denotes the vector norm, 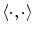 denotes the dot product,
denotes the dot product, 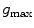 is the estimated mean amplitude of intensity gradients at vertebra boundaries that is used to suppresses the weighted gradients, which may occur if the gradient magnitude at the boundary of the object of interest is considerably smaller than of another object in its neighborhood (e.g. pedicle screws), and
is the estimated mean amplitude of intensity gradients at vertebra boundaries that is used to suppresses the weighted gradients, which may occur if the gradient magnitude at the boundary of the object of interest is considerably smaller than of another object in its neighborhood (e.g. pedicle screws), and  is the image appearance operator at candidate mesh centroid location
is the image appearance operator at candidate mesh centroid location 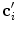 :
: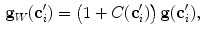
(5)
 is the intensity gradient at
is the intensity gradient at 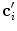 and
and ![$$C(\mathbf {c}_i') \in [0,1]$$](/wp-content/uploads/2016/10/A331518_1_En_8_Chapter_IEq59.gif) is the continuous response to the Canny edge operator [2]. By adding additional weights to the image intensity gradients, vertebra boundary points are more likely to be detected. In contrast to the original technique [9, 15], the size of the sampling parcel
is the continuous response to the Canny edge operator [2]. By adding additional weights to the image intensity gradients, vertebra boundary points are more likely to be detected. In contrast to the original technique [9, 15], the size of the sampling parcel  (Eq. 2) is reduced in each iteration
(Eq. 2) is reduced in each iteration  and the image intensity gradients
and the image intensity gradients  (Eq. 5) are additionally weighted, both to improve the accuracy of the resulting segmentation.
(Eq. 5) are additionally weighted, both to improve the accuracy of the resulting segmentation.