(1)
Faculty of Medicine, Department, of Oncology and Medical Physics Unit, McGill University, Montreal, Québec, Canada
Abstract
Chapter 6 consists of 22 problems covering 11 sections devoted to general aspects of charged particle interactions with matter. A charged particle is sur-rounded by its Coulomb electric field that interacts with orbital electrons and the nucleus of all atoms it encounters as it penetrates into an absorber. Charged particle interactions with orbital electrons of the absorber result in collision loss; interactions with nuclei of the absorber result in radiation loss.
The energy transfer from the charged particle to matter in each individual atomic interaction is generally small, so that the particle undergoes a large number of interactions before its kinetic energy is fully spent. The parameter that is used to describe the gradual loss of energy of the charged particle, as it penetrates into an absorber, is referred to as stopping power. Two categories of stopping power are known: (1) collision stopping power that results from charged particle interaction with orbital electrons of the absorber atoms and (2) radiation stopping power that results from charged particle interaction with the nuclei of the absorber.
Chapter 6 starts with problems dealing with general aspects of energy transfer from charged particle to absorber and with general aspects of stopping power of absorbers (Sects. 6.1 and 6.2). Section 6.3 covers radiation stopping power and is followed by several problems on collision stopping power of absorbing media for heavy charged particles in Sect. 6.4 and for light charged particles in Sect. 6.5. Section 6.6 deals with total stopping power and the chapter concludes with problems related to various aspects of stopping power, such as radiation yield (Sect. 6.7), range of charged particle in absorber (Sect. 6.8), mean and restricted stopping power (Sects. 6.9 and 6.10) and practical aspects of bremsstrahlung targets (Sect. 6.11).
Chapter 6 consists of 22 problems covering 11 sections devoted to general aspects of charged particle interactions with matter. A charged particle is sur-rounded by its Coulomb electric field that interacts with orbital electrons and the nucleus of all atoms it encounters as it penetrates into an absorber. Charged particle interactions with orbital electrons of the absorber result in collision loss; interactions with nuclei of the absorber result in radiation loss.
The energy transfer from the charged particle to matter in each individual atomic interaction is generally small, so that the particle undergoes a large number of interactions before its kinetic energy is fully spent. The parameter that is used to describe the gradual loss of energy of the charged particle, as it penetrates into an absorber, is referred to as stopping power. Two categories of stopping power are known: (1) collision stopping power that results from charged particle interaction with orbital electrons of the absorber atoms and (2) radiation stopping power that results from charged particle interaction with the nuclei of the absorber.
Chapter 6 starts with problems dealing with general aspects of energy transfer from charged particle to absorber and with general aspects of stopping power of absorbers (Sects. 6.1 and 6.2). Section 6.3 covers radiation stopping power and is followed by several problems on collision stopping power of absorbing media for heavy charged particles in Sect. 6.4 and for light charged particles in Sect. 6.5. Section 6.6 deals with total stopping power and the chapter concludes with problems related to various aspects of stopping power, such as radiation yield (Sect. 6.7), range of charged particle in absorber (Sect. 6.8), mean and restricted stopping power (Sects. 6.9 and 6.10) and practical aspects of bremsstrahlung targets (Sect. 6.11).
6.1 General Aspects of Energy Transfer from Charged Particle to Medium
6.1.Q1 (127)
A charged particle (CP) is surrounded by its Coulomb electric field that interacts with orbital electrons and the nucleus of all atoms it encounters, as it penetrates into an absorbing medium. In penetrating an absorber charged particles may experience a variety of interactions with atoms of the medium. Energy transfer from the charged particle to absorbing medium in each individual atomic interaction is generally but not necessarily small, so that the energetic particle typically undergoes a large number of interactions before its incident kinetic energy is fully spent.
(a)
Classify charged particles used in medicine for treatment of disease according to their mass.
(b)
Classify charged particle interactions with absorber atoms and provide a brief description of each interaction.
(c)
Prepare a block diagram for interactions between a charged particle and absorber atom listed in (b).
(d)
Of the CP interactions listed in (b) only a few contribute to CP energy loss. List and rank the energy loss processes in CP interactions with absorber atoms.
SOLUTION:
(a) Charged particles (CPs) of interest in medicine for treatment of disease are usually placed into three categories according to their rest mass:
In 1970s negative pions were touted as an exciting charged particle option for use in radiotherapy, however, during the past two decades the study of negative pions has largely been abandoned in favor of heavy charged particles such as protons because of simpler means of production and less expensive equipment maintenance.
(1)
Light charged particles (CPs), such as electrons and positrons with rest mass of m e=0.511 MeV/c 2.
(2)
Intermediate charged particles (CPs), such as negative pions π − with 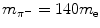 .
.
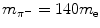 .
.(3)
Heavy charged particles (CPs), such as protons (m p=1836m e), deuterons, α particles, carbon ions, etc.
(b) As energetic charged particles penetrate into an absorbing medium, they interact either with orbital electrons of absorber atoms or with the nucleus of absorbing atoms. These interactions are typically classified as follows:
(c) A block diagram of interactions between charged particle and atom is shown in Fig. 6.1.
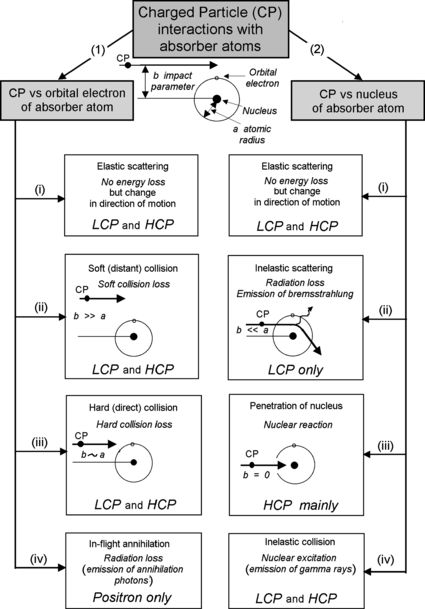
(1)
Coulomb interaction between CP and orbital electrons of absorber atom resulting in:
(i)
Elastic scattering (no energy loss but change in direction of motion).
(ii)
Inelastic collision referred to as soft or distant collision with impact parameter b much larger than radius of absorbing atom a, i.e., b≫a, resulting in some energy loss (soft collision loss) through excitation or ionization of absorber atom.
(iii)
Inelastic collision referred to as hard or direct collision with impact parameter b of the order of the radius of absorbing atom a, i.e., b≈a, resulting in some energy loss (hard collision loss) through excitation or ionization of absorber atom.
(iv)
In-flight annihilation (applicable to positrons only) of CP with orbital electron of absorber resulting in production of annihilation photons (radiation loss).
(2)
Coulomb interaction between CP and nucleus of absorber atom resulting in:
(i)
Elastic scattering (essentially no energy loss but change in direction of motion).
(ii)
Inelastic scattering referred to as radiation loss with the impact parameter b much smaller than the radius of the absorber atom a, i.e., b≪a, resulting in energy loss through production of bremsstrahlung (applicable to light CPs only).
(iii)
Penetration of the nucleus of absorbing atom resulting in nuclear reaction (applicable to heavy and intermediate CPs and much less so to light CP).
(iv)
Inelastic scattering resulting in Coulomb nuclear excitation and subsequent emission of gamma rays.

Fig. 6.1
Classification of charged particle (CP) interactions with absorber atoms. Intermediate CPs are ignored because they are no longer considered an option for radiotherapy. LCP and HCP stand for “light charged particles” and “heavy charged particles”, respectively
(d) The four entries in CP vs orbital electron interaction and the four entries in CP vs nucleus interaction cover the most important interaction processes of CP interaction with absorber atoms. However, the cross sections for individual interactions vary significantly from one interaction to another and from one particle to another.
(1) CP interactions with orbital electrons of absorber atoms:
Elastic collisions are possible but essentially negligible except at very low CP energies where the process is referred to as the Ramsauer effect.
Inelastic collisions represent the prevalent interaction between the CP and orbital electrons of the absorber and are split into two classes: hard and soft collisions, both classes causing excitation and ionization of absorber atoms. The energy transfer to orbital electrons is significantly higher in hard collisions in comparison to soft collisions; however, the number of soft collisions exceeds the number of hard collisions to such an extent that total energy transfer from the CP to orbital electrons of the absorber is roughly equal for the two classes of collision.
In-flight annihilation only applies to light CP and of these, only to positrons. It produces radiation loss that is added to the bremsstrahlung loss but contributes only a small amount to the total radiation loss and is often ignored in comparison with hard and soft collision loss.
(2) CP interactions with nuclei of absorber atoms:
Elastic Coulomb scattering of CPs on nuclei of absorber atoms are not pronounced for heavy CPs but are very pronounced for light CPs because of their relatively small mass in comparison to that of nuclei. For heavy CPs there is some energy transfer from the CP to the nucleus as the recoil energy of the nucleus but this recoil energy is miniscule in comparison to energy losses inelastic collisions between the heavy CP and orbital electrons of the absorber atoms
Inelastic Coulomb scattering of CPs on nuclei is much less probable than elastic Coulomb scattering. It can be ignored for heavy CPs but it is of significance for light CPs because it serves as source as source of bremsstrahlung photons that play a very important role in modern physics in particular as well as science, industry, and medicine in general.
Penetration of the nucleus by a heavy or light CP that engenders a nuclear reaction is very important in its own right in nuclear physics but play only a minor role in energy transfer from CP to absorber atom. Thus, in energy transfer considerations this process is usually neglected.
Coulomb nuclear excitation by a heavy or light CP is of interest in nuclear physics but is of negligible importance in energy transfer considerations and is therefore ignored.
In summary, the most important processes of energy transfer from CP to atoms of absorber are the inelastic hard and soft collisions between the CP and orbital electrons of absorber engendering collision (ionization) loss and inelastic collisions between the CP and nucleus of absorber atoms engendering radiation (bremsstrahlung) loss.
6.2 General Aspects of Stopping Power
6.2.Q1 (128)
Stopping power plays an important role in study of charged particle interactions with absorbing media.
(a)
Define stopping power and explain the purpose it serves.
(b)
List and briefly describe the various known types of stopping power.
(c)
Mass stopping power S depends on physical properties of the absorber and the type of CP, yet, for a given heavy CP, it is constant within a factor of 2 for all absorbers. Explain.
SOLUTION:
(a) In traversing an absorbing medium a charged particle (CP) interacts with the atoms of the absorber and gradually loses its kinetic energy in a large number of small steps. The mean rate of energy loss per unit path length of the CP of kinetic energy E K traversing an absorbing medium of atomic number Z is defined as the stopping power of the absorbing medium. Stopping power depends on physical properties of the absorbing medium as well on properties of the CP traversing the absorbing medium. Stopping power is considered a property of the absorbing medium in which a CP propagates.
Stopping power has an important role in many facets of basic science and technology, and is used heavily in clinical radiation dosimetry based on ionization chambers.
(b) Various types of stopping power are known depending on: (1) the expression of path length of the CP propagating in the absorbing medium and (2) the mode of CP interaction with the atoms of the absorbing medium.
(1) With regard to penetration path length two types of stopping power are known:
The rate of energy loss (typically expressed in MeV) per unit penetration path length (typically expressed in cm) is called the “linear stopping power” s. Linear stopping power is proportional to the number of absorber atoms N a per volume 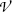 and its typical units are MeV/cm and less commonly keV/μm. Since
and its typical units are MeV/cm and less commonly keV/μm. Since 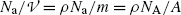 , one concludes that the linear stopping power s is proportional to absorber density ρ and inversely proportional to its atomic mass number A. N A is the Avogadro constant.
, one concludes that the linear stopping power s is proportional to absorber density ρ and inversely proportional to its atomic mass number A. N A is the Avogadro constant.
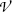 and its typical units are MeV/cm and less commonly keV/μm. Since
and its typical units are MeV/cm and less commonly keV/μm. Since 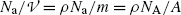 , one concludes that the linear stopping power s is proportional to absorber density ρ and inversely proportional to its atomic mass number A. N A is the Avogadro constant.
, one concludes that the linear stopping power s is proportional to absorber density ρ and inversely proportional to its atomic mass number A. N A is the Avogadro constant.To minimize the effect of absorber density ρ on stopping power the penetration path length is often measured in g/cm2 and the energy loss per unit path length is then called the “mass stopping power” S with typical unit MeV⋅cm2/g. The mass stopping power S is thus proportional to the number of absorber atoms N a per absorber mass m that is proportional to N A/A. In mass stopping power S the effect of absorber density is removed and the mass stopping power of all absorber materials is, within a factor of 2, constant for all absorbers.
Linear and mass stopping powers are thus defined as
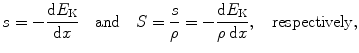
where dE K is the energy lost by the CP in absorbing medium at penetration thickness dx.
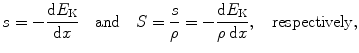
(6.1)
(2) With regard to mode of interaction between the CP and atoms of absorbing medium the stopping power is divided into two major groups: inelastic collision interaction between CP and orbital electrons of the absorber result in collision (also referred to as electronic or ionization) stopping power; inelastic collision interaction between the CP and nucleus of absorber result in radiation stopping power. Inelastic collisions between CP and orbital electrons are further subdivided into soft collisions and hard collisions that result in hard collision stopping power and soft collision stopping power, as shown schematically in Fig. 6.2.
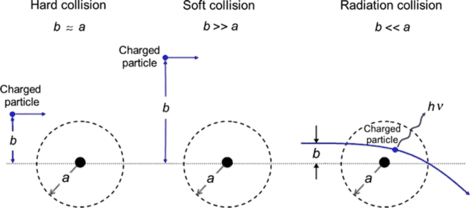

Fig. 6.2
Three different types of collision (hard, sof, and radiation collision) of a charged particle with a atom depending on the relative size of the impact parameter b and atomic radius a
Total stopping power S tot is defined as the sum of radiation stopping power S rad and collision stopping power S col consisting of a soft and a hard term. We thus have
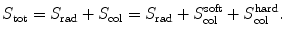
(c) For heavy CPs the mass radiation stopping power S rad is much smaller than the mass collision stopping power S col, so that the total mass stopping power S tot is roughly equal to S col. Since S col originates with inelastic collisions between the CP and orbital electrons of the absorber atoms, a conclusion can be made that S col is proportional to the electron density N e given as the number of electrons per mass of the absorber or N e/m=ZN A/A. Since Z/A is roughly constant in nature, slowly varying from 0.5 for low Z elements down to ∼0.38 for high Z elements, we conclude that Z/A≈0.5 (with one notable exception of hydrogen for which Z/A=1) and, therefore, S col should not vary appreciably with atomic number of absorbers for a given CP of a given kinetic energy E K. However, theoretical derivations of S col reveal other Z-dependent terms that cause a decrease in S col with increasing atomic number Z of the absorber.
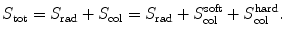
(6.2)
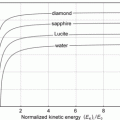
This conclusion is substantiated in Table 6.1 and Fig. 6.3 that give S col against E K for protons in the range from 1 keV to 104 MeV for various absorber materials ranging from hydrogen (Z=1) to uranium (Z=92) in addition to water and air. Data are from the NIST www.physics.nist.gov/PhysRefData/Star/Text/PSTAR.html
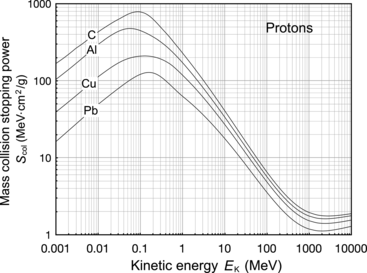

Fig. 6.3
Mass collision stopping power, i.e., total mass stopping power of various absorbing materials for protons against proton kinetic energy in the range from 1 keV to 104 MeV
Table 6.1
Collision stopping powers in MeV⋅cm2/g of various materials for protons of various kinetic energies in the range from 0.1 MeV to 1 GeV. Date are from the NIST
Element | Atomic number | 0.1 MeV | 1 MeV | 10 MeV | 100 MeV | 1000 MeV |
|---|---|---|---|---|---|---|
Hydrogen | 1 | 3487 | 676.4 | 101.9 | 15.2 | 4.50 |
Carbon | 6 | 719 | 226.3 | 40.5 | 6.49 | 1.94 |
Aluminum | 13 | 447.7 | 172.0 | 33.7 | 5.68 | 1.75 |
Copper | 29 | 209.3 | 118.2 | 27.1 | 4.85 | 1.52 |
Silver | 47 | 195.5 | 96.1 | 23.1 | 4.34 | 1.39 |
Tungsten | 74 | 116.3 | 63.5 | 18.2 | 3.70 | 1.22 |
Lead | 82 | 121.4 | 63.0 | 17.8 | 3.55 | 1.19 |
Uranium | 92 | 141 | 58.8 | 16.9 | 3.41 | 1.14 |
Water | 816 | 260.8 | 45.6 | 7.29 | 2.21 | |
Air | 730 | 222.9 | 40.1 | 6.44 | 1.96 |
6.3 Radiation Stopping Power
6.3.Q1 (129)
According to Bethe and Heitler the mass radiation stopping power S rad of an absorbing material traversed by light charged particles (electrons or positrons) of kinetic energy E K can be estimated with the following expression
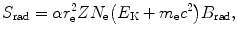
where
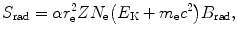
(6.3)
α
is the fine structure constant [α=e 2/(4πε 0 ħc)=1/137].
r e
is the classical electron radius [r e=e 2/(4πε 0 m e c 2)=2.818 fm].
N e
is the number of electrons per unit mass (electron density), i.e., N e=ZN A/A with Z and A, respectively, the atomic number and atomic mass of the absorber.
m e c 2
electron and positron rest energy (m e c 2=0.511 MeV).
B rad
is a slowly varying function of the atomic number Z of the absorber and total energy E i=E K+m e c 2 of the light charged particle (CP) with the following recommended mean values: 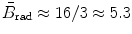 in the non-relativistic kinetic energy range where E K≪m e c 2;
in the non-relativistic kinetic energy range where E K≪m e c 2; 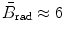 for E K≈1 MeV;
for E K≈1 MeV; 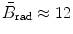 for E K≈10 MeV; and
for E K≈10 MeV; and 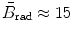 for E K≈100 MeV.
for E K≈100 MeV.
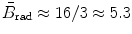 in the non-relativistic kinetic energy range where E K≪m e c 2;
in the non-relativistic kinetic energy range where E K≪m e c 2; 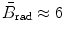 for E K≈1 MeV;
for E K≈1 MeV; 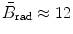 for E K≈10 MeV; and
for E K≈10 MeV; and 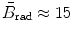 for E K≈100 MeV.
for E K≈100 MeV.(a)
Based on mass radiation stopping power S rad data available from the NIST and provided for electrons traversing four absorbers (carbon, copper, tin, and lead) in Table 6.2, determine numerical values for the function B rad(Z,E i) for the four absorbers at kinetic energies of E K=0.01 MeV, 0.1 MeV, 1 MeV, 10 MeV, and 100 MeV.
(b)
Describe the dependence of function B rad on kinetic energy E K of the incident electron and atomic number Z of the absorber.
(c)
Based on your calculations, determine average (mean) values of B rad and compare them to the values recommended in the literature and stated above.
Table 6.2
Mass radiation stopping power 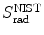 from the NIST of four absorbers (carbon, copper, tin, and lead) for five kinetic energies E K of the electron (0.01 MeV, 0.1 MeV, 1 MeV, 10 MeV, and 100 MV). E i stands for the total energy of the incident electron
from the NIST of four absorbers (carbon, copper, tin, and lead) for five kinetic energies E K of the electron (0.01 MeV, 0.1 MeV, 1 MeV, 10 MeV, and 100 MV). E i stands for the total energy of the incident electron
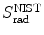 from the NIST of four absorbers (carbon, copper, tin, and lead) for five kinetic energies E K of the electron (0.01 MeV, 0.1 MeV, 1 MeV, 10 MeV, and 100 MV). E i stands for the total energy of the incident electron
from the NIST of four absorbers (carbon, copper, tin, and lead) for five kinetic energies E K of the electron (0.01 MeV, 0.1 MeV, 1 MeV, 10 MeV, and 100 MV). E i stands for the total energy of the incident electron1 | E K (MeV) | 0.01 | 0.1 | 1 | 10 | 100 | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
2 | E i (MeV) | 0.521 | 0.611 | 1.511 | 10.511 | 100.511 | |||||
3 | Absorber | 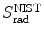 | 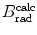 | 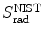 | 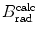 | 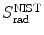 | 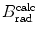 | 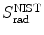 | 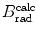 | 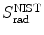 | 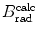 |
4 | Carbon C | 0.003 | 0.003 | 0.011 | 0.151 | 2.05 | |||||
5 | Copper Cu | 0.012 | 0.017 | 0.046 | 0.565 | 7.08 | |||||
6 | Tin Sn | 0.017 | 0.028 | 0.077 | 0.849 | 10.40 | |||||
7 | Lead Pb | 0.021 | 0.045 | 0.129 | 1.206 | 14.36 | |||||
SOLUTION:
(a) As given in (6.3), the mass radiation stopping power S rad contains a fundamental constant 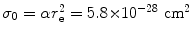 and is proportional to ZN e=Z 2 N A/A, total energy E i=E K+m e c 2 of the incident light CP (electron or positron), and function B rad. Since Table 6.2 provides S rad from the NIST evaluated with a combination of theoretical bremsstrahlung cross sections described by Berger and Seltzer, it is easy to determine the function B rad from (6.3) as follows
and is proportional to ZN e=Z 2 N A/A, total energy E i=E K+m e c 2 of the incident light CP (electron or positron), and function B rad. Since Table 6.2 provides S rad from the NIST evaluated with a combination of theoretical bremsstrahlung cross sections described by Berger and Seltzer, it is easy to determine the function B rad from (6.3) as follows
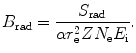
Before embarking on the calculation of B rad, we compile appropriate data for the four absorbers, such as Z, A, N e and 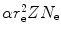 and present them in Table 6.3.
and present them in Table 6.3.
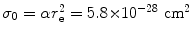 and is proportional to ZN e=Z 2 N A/A, total energy E i=E K+m e c 2 of the incident light CP (electron or positron), and function B rad. Since Table 6.2 provides S rad from the NIST evaluated with a combination of theoretical bremsstrahlung cross sections described by Berger and Seltzer, it is easy to determine the function B rad from (6.3) as follows
and is proportional to ZN e=Z 2 N A/A, total energy E i=E K+m e c 2 of the incident light CP (electron or positron), and function B rad. Since Table 6.2 provides S rad from the NIST evaluated with a combination of theoretical bremsstrahlung cross sections described by Berger and Seltzer, it is easy to determine the function B rad from (6.3) as follows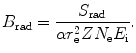
(6.4)
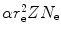 and present them in Table 6.3.
and present them in Table 6.3.Table 6.3
Basic atomic properties of the four absorbers: carbon, copper, tin, and lead
1 | Absorber | Atomic number Z | Atomic mass A | Electron density N e=ZN A/A | 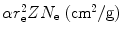 |
|---|---|---|---|---|---|
2 | Carbon C | 6 | 12.01 | 3.008×1023 | 1.046×10−3 |
3 | Copper Cu | 29 | 63.5 | 2.749×1023 | 4.623×10−3 |
4 | Tin Sn | 50 | 118.7 | 2.537×1023 | 7.352×10−3 |
5 | Lead Pb | 82 | 207.2 | 2.383×1023 | 11.33×10−3 |
We again note that N e in the first approximation equals to  ; however, a closer look shows that N e≈0.5 for low Z elements and then it slowly drops to reach N e≈0.4 for high Z elements. One can still state that S rad is approximately proportional to Z of the absorber; however, to make this statement with more confidence we need to examine the Z-dependence of B rad for a given kinetic energy of the incident electron or positron.
; however, a closer look shows that N e≈0.5 for low Z elements and then it slowly drops to reach N e≈0.4 for high Z elements. One can still state that S rad is approximately proportional to Z of the absorber; however, to make this statement with more confidence we need to examine the Z-dependence of B rad for a given kinetic energy of the incident electron or positron.
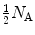 ; however, a closer look shows that N e≈0.5 for low Z elements and then it slowly drops to reach N e≈0.4 for high Z elements. One can still state that S rad is approximately proportional to Z of the absorber; however, to make this statement with more confidence we need to examine the Z-dependence of B rad for a given kinetic energy of the incident electron or positron.
; however, a closer look shows that N e≈0.5 for low Z elements and then it slowly drops to reach N e≈0.4 for high Z elements. One can still state that S rad is approximately proportional to Z of the absorber; however, to make this statement with more confidence we need to examine the Z-dependence of B rad for a given kinetic energy of the incident electron or positron.We now calculate B rad for each of the four absorbers at the five kinetic energies E K using (6.4) and data that are summarized in Table 6.3. The calculated B rad are displayed in Table 6.4.
Table 6.4
Calculated values of B rad for the four absorbers (carbon, copper, tin, and lead) at five kinetic energies E K of the electron. Mass radiation stopping powers S rad are from the NIST
1 | E K (MeV) | 0.01 | 0.1 | 1 | 10 | 100 | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
2 | E i (MeV) | 0.521 | 0.611 | 1.511 | 10.511 | 100.511 | |||||
3 | Absorber | 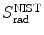 | 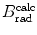 | 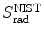 | 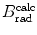 | 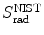 | 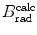 | 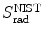 | 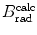 | 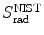 | 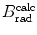 |
4 | Carbon C | 0.003 | 5.9 | 0.003 | 5.3 | 0.011 | 6.6 | 0.151 | 13.7 | 2.05 | 19.5 |
5 | Copper Cu | 0.012 | 5.1 | 0.017 | 6.1 | 0.046 | 6.6 | 0.565 | 11.6 | 7.08 | 15.2 |
6 | Tin Sn | 0.017 | 4.4 | 0.028 | 6.3 | 0.077 | 6.9 | 0.849 | 11.0 | 10.40 | 14.1 |
7 | Lead Pb | 0.021 | 3.5 | 0.045 | 6.4 | 0.129 | 7.5 | 1.206 | 10.1 | 14.36 | 12.6 |
(b) The dependence of the radiation stopping power B rad on kinetic energy E K of the light CP and atomic number Z of the absorber is determined from Fig. 6.4. The figure shows that for a given absorber Z at low kinetic energies E K where E K≪m e c 2 the parameter B rad amounts to about 5.5. With increasing E K the parameter remains almost constant and at E K≈m e c 2 begins to rise slowly to reach a value of 6 at E K≈1 MeV and then continues to rise slowly until it reaches saturation at around E K≈1000 MeV. For a given E K, on the other hand, B rad is essentially constant (∼5.5) at E K<1 MeV but at higher E K>1 MeV it is inversely proportional to Z with the spread in B rad increasing with increasing kinetic energy E K and amounting to ∼7±0.5 at E K=1 MeV; ∼12±2 at E K=10 MeV; ∼16±3.5 at E K=100 MeV; and ∼17.5±4 at E K=1000 MeV.
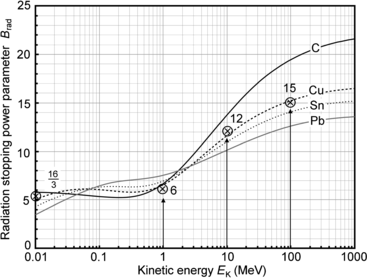

Fig. 6.4
Radiation stopping power parameter B rad against kinetic energy E K for four absorber materials: carbon, copper, tin, and lead. Symbols ⊗ indicate values of B rad at various kinetic energies E K as recommended in the literature
6.4 Collision (Electronic) Stopping Power for Heavy Charged Particles
6.4.Q1 (130)
Energy transfer from energetic heavy charged particles (CP) to a medium (absorber) they traverse occurs mainly through Coulomb interactions of the CP with orbital electrons of absorber atoms (collision or electronic loss); inelastic Coulomb interactions between heavy CP and nuclei of the absorber atoms (radiation loss) are negligible and thus ignored.
(a)
Plot a schematic diagram for a typical Coulomb interaction between a heavy CP and orbital electron of absorber that results in momentum transfer Δp and energy transfer ΔE from the CP to orbital electron. Clearly identify all parameters that influence the interaction.
(b)
For a heavy CP of charge ze and kinetic energy E K traversing an absorber of electron density N e derive expressions for momentum transfer Δp and energy transfer ΔE from the heavy CP to orbital electron of absorber. Express the impact parameter indeximpact parameter b as a function of Δp and ΔE.
(c)
Both Δp and ΔE depend on the impact parameter b and both have a range between a minimum and maximum value, corresponding to a maximum and minimum value of b, respectively. For the seven elements listed in Table 6.5 determine the maximum and minimum values of Δp, ΔE, and b for proton of incident kinetic energy E K=10 MeV.
(d)
Can an interaction between a heavy CP and absorber orbital electron occur when the impact parameter b is outside the range b min≤b≤b max? If so, what is the type of interaction? Do any interactions occur between the incident heavy CP and the nuclei of absorber atoms?
Table 6.5
Mean ionization/excitation potential I (eV) for various elements of interest to medical physics
1 | Element | H | Al | Cu | Ag | Au | W | Pb |
|---|---|---|---|---|---|---|---|---|
2 | Atomic number Z | 1 | 12 | 29 | 47 | 79 | 74 | 82 |
3 | Ionization/excitation potential I (eV) | 19 | 166 | 322 | 470 | 790 | 727 | 823 |
SOLUTION:
(a) Coulomb interaction between a heavy CP (charge ze and mass M) and an orbital electron (charge e and mass m e) of an absorber atom is shown schematically in Fig. 6.5. Base on assumption that the heavy CP is positively charged, the orbital electron is located in the inner focus of the hyperbolic trajectory that, in principle, the heavy CP follows. Note: if the two particle charges were of equal sign, then the stationary particle would reside in the outer focus of the hyperbola as is the case in Rutherford scattering. The important parameters of the Coulomb interaction are: impact parameter b, scattering angle θ, and angle ϕ between the radius vector r and the bisector of the hyperbolic trajectory of the CP.
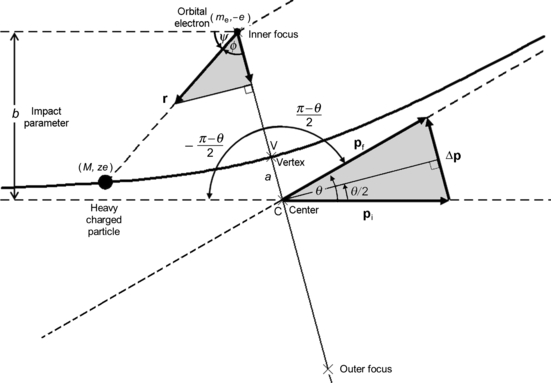

Fig. 6.5
Schematic diagram of a Coulomb collision between a positively charged heavy particle with mass M and an orbital electron with mass m e. Since M≫m e, the scattering angle θ≈0
(b) The momentum transfer (impulse) Δp from the CP to orbital electron is directed along a line that bisects the angle π−θ, where θ is the scattering angle for the Coulomb interaction
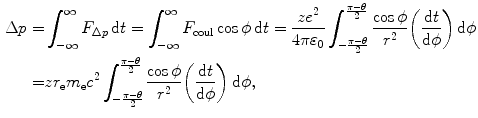
where
The Coulomb force between the two charges (ze and e) is given as
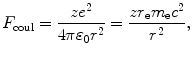
with r e the standard classical electron radius constant [r e=e 2/(4πε 0 m e c 2)=2.818 fm] and m e c 2 rest energy of the electron [m e c 2=0.511 MeV]. The angular momentum L for the Coulomb collision process is defined as follows (see Fig. T2.4)
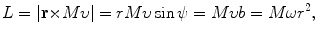
with
Using the conservation of angular momentum expressed in (6.7), we can now write (6.5) in a simpler form
![$$ \Delta p = \frac{zr_{\mathrm{e}}m_{\mathrm{e}}c^{2}}{\upsilon b}\int_{ - \frac{\pi - \theta}{2}}^{\frac{\pi - \theta}{2}} \cos \phi \,\mathrm{d}\phi = \frac{zr_{\mathrm{e}}m_{\mathrm{e}}c^{2}}{\upsilon b}[\sin \phi ]_{ - (\pi - \theta )/2}^{(\pi - \theta )/2} = \frac{2zr_{\mathrm{e}}m_{\mathrm{e}}c^{2}}{\upsilon b}\cos \frac{\theta}{2}. $$](/wp-content/uploads/2016/04/A212719_1_En_6_Chapter_Equ8.gif)
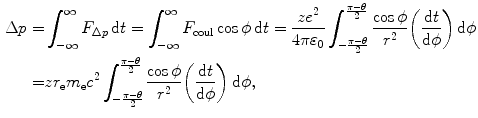
(6.5)
r
is the distance between the heavy CP and the orbital electron.
ϕ
is the angle between the radius vector r and the bisector of the hyperbola.
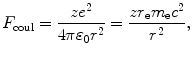
(6.6)
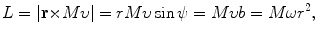
(6.7)
ω
angular frequency equal to dϕ/dt.
υ
velocity of the heavy CP before the interaction.
b
impact parameter.
![$$ \Delta p = \frac{zr_{\mathrm{e}}m_{\mathrm{e}}c^{2}}{\upsilon b}\int_{ - \frac{\pi - \theta}{2}}^{\frac{\pi - \theta}{2}} \cos \phi \,\mathrm{d}\phi = \frac{zr_{\mathrm{e}}m_{\mathrm{e}}c^{2}}{\upsilon b}[\sin \phi ]_{ - (\pi - \theta )/2}^{(\pi - \theta )/2} = \frac{2zr_{\mathrm{e}}m_{\mathrm{e}}c^{2}}{\upsilon b}\cos \frac{\theta}{2}. $$](/wp-content/uploads/2016/04/A212719_1_En_6_Chapter_Equ8.gif)
(6.8)
In the case of heavy CP of charge ze and mass M interacting with a “stationary” electron of charge e and mass m e, the scattering angle θ is essentially equal to zero because M≫m e. Thus, the momentum transfer Δp from (6.8) and energy transfer ΔE, respectively, are given as
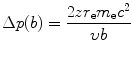
and
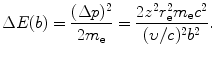
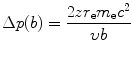
(6.9)
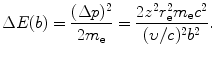
(6.10)
The impact parameter b as a function of Δp and ΔE can thus be expressed from (6.9) and (6.10) as follows
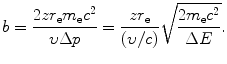
(c) Intuitively, we might assume that the impact parameter b ranges from 0 to ∞ and that the energy transfer ΔE ranges from 0 to E K, the kinetic energy of the incident heavy CP. However, a closer look at the underlying physics reveals that ΔE actually ranges from a minimum ΔE min>0 to a maximum ΔE max<E K both clearly defined and corresponding to maximum and minimum values of b, respectively. Minimum energy transfer ΔE min is limited to the mean ionization/excitation potential I of the given absorber and ΔE max is limited by the maximum energy that can be transferred from particle M 0 to particle m 0 in a direct-hit collision, classically given as ΔE max=2m e υ 2 [see (T5.30)]. Using (6.9), (6.10), and (6.11) we can now express the minima and maxima in Δp, ΔE, and b as follows
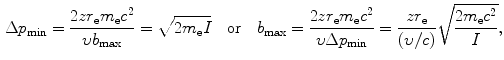
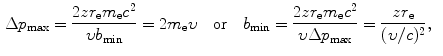
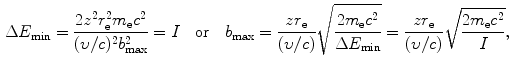
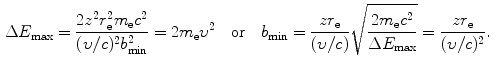
Using the expressions above, we will determine the minima and maxima as follows: ![$\Delta p_{\min } = [ \sqrt{m_{\mathrm{e}}c^{2}I} ]/c$](/wp-content/uploads/2016/04/A212719_1_En_6_Chapter_IEq34.gif) ; Δp max=2m e c 2(υ/c)/c;ΔE min=I; ΔE max=2m e c 2(υ/c)2; b min=zr e(υ/c)−2; and
; Δp max=2m e c 2(υ/c)/c;ΔE min=I; ΔE max=2m e c 2(υ/c)2; b min=zr e(υ/c)−2; and ![$b_{\max } = [zr_{\mathrm{e}}/(\upsilon /c)]\sqrt{2m_{\mathrm{e}}c^{2}/I}$](/wp-content/uploads/2016/04/A212719_1_En_6_Chapter_IEq35.gif) . From these expressions it is evident that, on the one hand, the minima in Δp and ΔE are independent of the CP and depend only on the mean ionization/excitation potential I of the absorber; while, on the other hand, the maxima in Δp and ΔE are independent of the absorber but depend on the velocity υ of the CP. Results of these calculations are given in Table 6.6.
. From these expressions it is evident that, on the one hand, the minima in Δp and ΔE are independent of the CP and depend only on the mean ionization/excitation potential I of the absorber; while, on the other hand, the maxima in Δp and ΔE are independent of the absorber but depend on the velocity υ of the CP. Results of these calculations are given in Table 6.6.
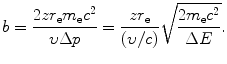
(6.11)
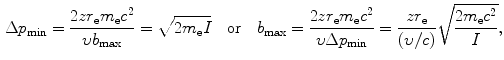
(6.12)
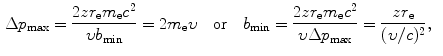
(6.13)
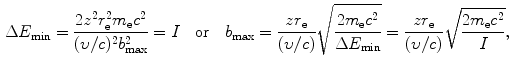
(6.14)
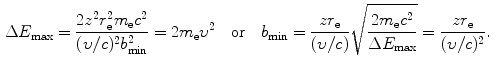
(6.15)
![$\Delta p_{\min } = [ \sqrt{m_{\mathrm{e}}c^{2}I} ]/c$](/wp-content/uploads/2016/04/A212719_1_En_6_Chapter_IEq34.gif) ; Δp max=2m e c 2(υ/c)/c;ΔE min=I; ΔE max=2m e c 2(υ/c)2; b min=zr e(υ/c)−2; and
; Δp max=2m e c 2(υ/c)/c;ΔE min=I; ΔE max=2m e c 2(υ/c)2; b min=zr e(υ/c)−2; and ![$b_{\max } = [zr_{\mathrm{e}}/(\upsilon /c)]\sqrt{2m_{\mathrm{e}}c^{2}/I}$](/wp-content/uploads/2016/04/A212719_1_En_6_Chapter_IEq35.gif) . From these expressions it is evident that, on the one hand, the minima in Δp and ΔE are independent of the CP and depend only on the mean ionization/excitation potential I of the absorber; while, on the other hand, the maxima in Δp and ΔE are independent of the absorber but depend on the velocity υ of the CP. Results of these calculations are given in Table 6.6.
. From these expressions it is evident that, on the one hand, the minima in Δp and ΔE are independent of the CP and depend only on the mean ionization/excitation potential I of the absorber; while, on the other hand, the maxima in Δp and ΔE are independent of the absorber but depend on the velocity υ of the CP. Results of these calculations are given in Table 6.6.Table 6.6
Mean ionization/excitation potential I, minimum and maximum momentum transfer (Δp min and Δp max), minimum and maximum energy transfer (ΔE min and ΔE max), and minimum and maximum impact parameter (b min and bmax) for 10 MeV proton traversing various absorbers of interest to medical physics
1 | Element | H | Al | Cu | Ag | W | Au | Pb |
|---|---|---|---|---|---|---|---|---|
2 | Z | 1 | 12 | 29 | 47 | 74 | 79 | 82 |
3 | I (eV) | 19 | 166 | 322 | 470 | 727 | 790 | 823 |
4 | Δp min (keV/c) | 3.12 | 9.21 | 12.83 | 15.50 | 19.27 | 20.09 | 20.51 |
5 | Δp max (keV/c) | ←151.2→ | ||||||
6 | ΔE min (eV) | 19 | 166 | 322 | 470 | 727 | 790 | 823 |
7 | ΔE max (eV) | ←21.5×103→ | ||||||
8 | b min (fm) | ←268→ | ||||||
9 | b max (fm) | 8832 | 2988 | 2145 | 1176 | 1428 | 1370 | 1342 |
(c) To work on our problem involving a 10 MeV proton and various absorbers we will first determine the proton velocity β=υ/c at E K=10 MeV. Velocity is determined using the relativistic expression for kinetic energy E K=(γ−1)m p c 2 to get
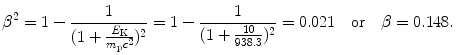
(d) The range of impact parameters b is from b=0 to b=∞; however, we must recognize that energy transfer ΔE from the CP to orbital electrons of the absorber atoms can occur only for impact parameters b in a much narrower window that extends from b min to b max, as shown for 10 MeV proton in various absorber materials in Table 6.6. The table also shows that ΔE max which is inversely proportional to b min is independent of absorber and depends only on the velocity υ of the CP, while ΔE min which is inversely proportional to b max depends on the absorber through the mean ionization/excitation potential I.
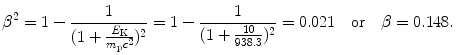
(6.16)
The answer to the question on whether or not a Coulomb interaction between a heavy CP and orbital electron is possible for impact parameters b outside the window b min≤b≤b max is that it certainly can occur; however, in this situation the interaction will be elastic and no energy transfer to absorber will occur. We also note that interactions between the CP and nuclei of the absorber certainly do occur, however, again, these interactions are elastic interactions that do not result in bremsstrahlung production.
6.4.Q2 (131)
The Bethe equation for collision stopping power S col of an absorbing medium for a heavy charged particle (CP) such as proton, deuteron and α particle and heavier ions such as carbon ion and neon ion is in the most general form that includes the Fano corrections written as
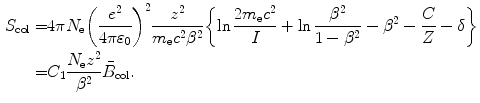
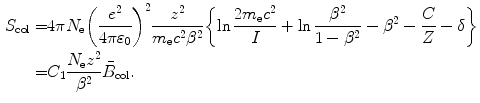
(6.17)
(a)
Identify parameters, define constants, and provide numerical values of constants for the collision stopping power equation (6.17).
(e)
SOLUTION:
(a) Parameters of the general Bethe equation incorporating the Fano corrections are as follows:
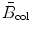
(b) Shell correction. Bethe’s derivation of S col for heavy CPs traversing an absorber assumes that the velocity υ of the CP is much larger than the velocity υ orb of orbital electrons of the absorber atoms. At high kinetic energy E K of the CP this assumption (υ≫υ orb) is correct; however, at low E K where υ≤υ orb it does not hold, since orbital electrons do not participate in energy transfer from the CP when υ≤υ orb. This effect causes an overestimate in the mean ionization/excitation potential I at low E K and, consequently, results in an underestimate in S col calculated from an uncorrected Bethe equation.
N e
electron density (N e=ZN A/A) expressed in number of electrons per gram of absorber medium with Z the atomic number and A the atomic mass of the absorber. In the first approximation, Z/A≈0.5 for all elements with the notable exception of hydrogen for which Z/A≈1. A closer look at Z/A shows that for Z≥2 it slowly decreases from 0.5 for low Z elements to 0.38 for high Z elements. For example, Z/A for helium-4 is 0.5, for cobalt-60 it is 0.45, and for uranium-235 it is 0.39.
ze
charge of the heavy charged particle CP (for proton z=1; for α particle z=2).
m e c 2
rest energy of the electron (m e c 2=0.511 MeV).
β
velocity of the heavy CP normalized to speed of light c=3×108 m/s in vacuum.
I
mean ionization/excitation potential of the absorber.
C
shell correction constant.
δ
density correction.
C 1
is a collision stopping power constant independent of absorbing medium as well as of the physical characteristics of the CP. It is defined with the following expression
![$$ \begin{aligned}[b] C_{1} &= 4\pi \biggl( \frac{e^{2}}{4\pi \varepsilon _{0}} \biggr)^{2}\frac{1}{m_{\mathrm{e}}c^{2}} = 4\pi \biggl[ \biggl( \frac{e^{2}}{4\pi \varepsilon _{0}} \biggr)\frac{1}{(m_{\mathrm{e}}c^{2})} \biggr]^{2}m_{\mathrm{e}}c^{2} = 4 \pi r_{\mathrm{e}}^{2}m_{\mathrm{e}}c^{2} \\ &= 4\pi {\times} \bigl(2.818 {\times} 10^{ - 13}\ \mathrm{cm} \bigr)^{2} {\times} (0.511\ \mathrm{MeV}) \,{=}\, 5.099 {\times} 10^{ - 25}\ \mathrm{MeV} \,{\cdot}\, \mathrm{cm}^{2}, \end{aligned} $$](/wp-content/uploads/2016/04/A212719_1_En_6_Chapter_Equ18.gif)
where r e is the classical radius of electron defined as
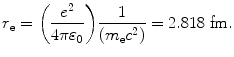
![$$ \begin{aligned}[b] C_{1} &= 4\pi \biggl( \frac{e^{2}}{4\pi \varepsilon _{0}} \biggr)^{2}\frac{1}{m_{\mathrm{e}}c^{2}} = 4\pi \biggl[ \biggl( \frac{e^{2}}{4\pi \varepsilon _{0}} \biggr)\frac{1}{(m_{\mathrm{e}}c^{2})} \biggr]^{2}m_{\mathrm{e}}c^{2} = 4 \pi r_{\mathrm{e}}^{2}m_{\mathrm{e}}c^{2} \\ &= 4\pi {\times} \bigl(2.818 {\times} 10^{ - 13}\ \mathrm{cm} \bigr)^{2} {\times} (0.511\ \mathrm{MeV}) \,{=}\, 5.099 {\times} 10^{ - 25}\ \mathrm{MeV} \,{\cdot}\, \mathrm{cm}^{2}, \end{aligned} $$](/wp-content/uploads/2016/04/A212719_1_En_6_Chapter_Equ18.gif)
(6.18)
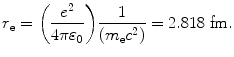
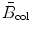
is the so-called atomic stopping number that depends directly on velocity β of the charged particle and indirectly on the atomic number Z of the absorber through the mean ionization/excitation potential I. It is given as
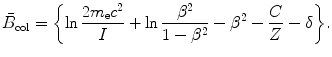
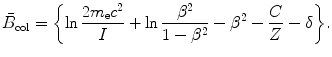
(6.19)
Since K shell electrons are the fastest of all orbital electrons in an absorber atom, they are the first to be affected by low CP velocity with decreasing CP velocity, as the CP penetrates deeper into the absorber. Often thus, the shell correction is addressed as the K shell correction and all possible higher shell corrections are ignored.
The shell correction term C/Z that Fano introduced to correct for the overestimate in I is a function of the absorbing medium as well as of the incident particle velocity υ; however, for the same absorbing medium and the same particle velocity, it is the same for all particles including electrons and positrons.
(c) Density effect correction. Fano introduced a second correction term δ to the Bethe collision stopping power equation to account for the polarization or density effect in condensed absorbing media. The effect influences the soft (distant) collision interactions by polarizing the condensed absorbing medium thereby decreasing the collision stopping power of the condensed medium in comparison with the same absorbing medium in the gaseous state. For heavy CPs the density correction is important at relativistic energies and negligible at intermediate and low energies; however, for electrons and positrons it plays a role in stopping power formulas at all energies.
(d) Dependence of S col on the absorbing medium. S col depends on atomic number Z of the absorber in two ways: (1) directly through the electron density N e=ZN A/A of the absorber and (2) indirectly through the mean ionization/excitation potential I of the absorber.
S col is directly proportional to Z/A and this implies that S col decreases with increasing Z as a result of the slight Z/A dependence on Z. Note: for hydrogen Z/A=1, but for all other elements, it is close to 0.5 ranging from 0.5 for low Z elements and, with increasing Z, slowly decreasing to ∼0.4 for high Z elements.
The indirect dependence of S col on absorber Z is brought about through the −lnI term in the stopping number 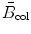 , since I depends on Z, ranging from 19 eV for hydrogen (Z=1) to ∼900 eV for uranium (Z=92). Thus, both the direct and indirect dependence of S col on atomic number Z of the absorber causes S col to diminish with increasing Z, however, the decrease in S col is only slight despite the two orders of magnitude range in atomic number Z of the absorber.
, since I depends on Z, ranging from 19 eV for hydrogen (Z=1) to ∼900 eV for uranium (Z=92). Thus, both the direct and indirect dependence of S col on atomic number Z of the absorber causes S col to diminish with increasing Z, however, the decrease in S col is only slight despite the two orders of magnitude range in atomic number Z of the absorber.
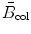 , since I depends on Z, ranging from 19 eV for hydrogen (Z=1) to ∼900 eV for uranium (Z=92). Thus, both the direct and indirect dependence of S col on atomic number Z of the absorber causes S col to diminish with increasing Z, however, the decrease in S col is only slight despite the two orders of magnitude range in atomic number Z of the absorber.
, since I depends on Z, ranging from 19 eV for hydrogen (Z=1) to ∼900 eV for uranium (Z=92). Thus, both the direct and indirect dependence of S col on atomic number Z of the absorber causes S col to diminish with increasing Z, however, the decrease in S col is only slight despite the two orders of magnitude range in atomic number Z of the absorber.(e) Dependence of S col on physical characteristic of the charged particle.
(1) As shown in (6.17), S col depends on CP velocity υ and charge ze but does not depend either directly or indirectly on the rest mass m 0 c 2 of the CP. A given absorbing material will have the same S col for all heavy CPs of a given kinetic energy E K and charge ze.
(2) Discussion of S col dependence on velocity υ must address three ranges in CP velocity: classical velocity υ at low kinetic energy, intermediate velocity at intermediate kinetic energy, and relativistic velocity at high energy. Each one of these three velocity ranges is characterized with its own effect on S col. As evident from (6.17), S col depends on CP velocity β=υ/c through the 1/β 2 term as well as through the {ln[β 2/(1−β 2)]−β 2} term contained in the atomic stopping number 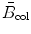 .
.
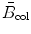 .
.At low kinetic energies E K the Fano shell correction must be incorporated in the Bethe equation to account for the low velocity υ of the CP and for non-participation of inner shell electrons in the stopping power process. In the intermediate energy region S col is governed by the 1/β 2 term that is proportional to 1/E K and decreases rapidly with increasing E K. In the high-energy relativistic region, where β≈1, collision stopping power S col rises slowly with E K as a result of the slow rise in the {ln[β 2/(1−β 2)]−β 2} term which slowly increases with E K.
(3) As far as the charge dependence of S col is concerned, we see from (6.17) that S col is linearly proportional to z 2 where ze stands for the charge of the CP. For example, z=1 for proton and deuteron; z=2 for α particle but z=1 for singly ionized helium atom; and z=1 for singly ionized carbon atom, z=2 for doubly ionized carbon atom, and z=6 for carbon nucleus. This implies, for example, that S col of an absorber will differ by a factor of 4 in the case of proton and α particle of the same velocity β, i.e., S col(α)=4S col(p) for the same β.
6.4.Q3 (132)
Several empirical expressions have been proposed for calculation of the mean atomic ionization/excitation potential I that is used in calculations of collision stopping power equations. A few of these approximations are as follows:
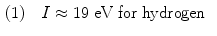
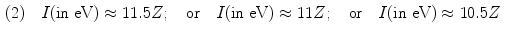
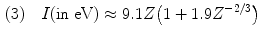
![$$\begin{aligned} (4) &\quad I(2 \le Z \le 13) \approx 11.2 + 11.7Z\quad \mbox{and}\quad I(Z > 13) \approx 52.8 + 8.71Z \end{aligned}$$ ” src=”/wp-content/uploads/2016/04/A212719_1_En_6_Chapter_Equ23.gif”></DIV></DIV><br />
<DIV class=EquationNumber>(6.23)</DIV></DIV><br />
<DIV id=Equ24 class=Equation><br />
<DIV class=EquationContent><br />
<DIV class=MediaObject><IMG alt=]() 13) = 9.76Z + 58.8Z^{ – 0.19} \end{aligned}$$ ” src=”/wp-content/uploads/2016/04/A212719_1_En_6_Chapter_Equ24.gif”>
13) = 9.76Z + 58.8Z^{ – 0.19} \end{aligned}$$ ” src=”/wp-content/uploads/2016/04/A212719_1_En_6_Chapter_Equ24.gif”>
Mean ionization/excitation potential I for chemical compounds such as water and for gas mixtures such as air are calculated with the Bragg additivity rule using the following expression
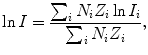
where
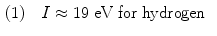
(6.20)
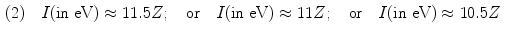
(6.21)
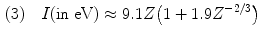
(6.22)
(6.24)
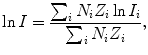
(6.25)
i
designates an individual component of the chemical compound or of the gas mixture
Z i
is the atomic number of the individual component i
N i
is the number of atoms i in the chemical component or the percentage by weight of the component i in the gas mixture.
SOLUTION:
Before using (6.25) we must determine the mean atomic ionization/excitation potential for the following elements: hydrogen and oxygen as constituents of water (H2O) and hydrogen, carbon, and oxygen as constituents of Lucite (C5H8O2) n . The appropriate data are presented in Table 6.7.
(a) Mean ionization/excitation potential of water is calculated from (6.25) as follows: We first calculate the two components of (6.25) and get
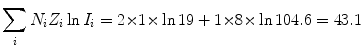
and
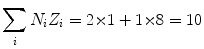
and then use (6.25) to get
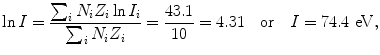
in good agreement with the value of 75 eV that is in common use for the mean ionization/excitation potential of water.
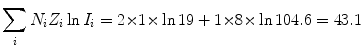
(6.26)
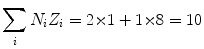
(6.27)
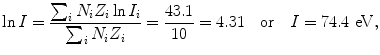
(6.28)
(b) Mean ionization/excitation potential I of Lucite (C5H8O2) n is also calculated from (6.25) by first calculating the numerator and denominator of (6.25), respectively
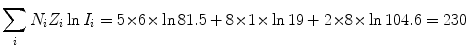
and
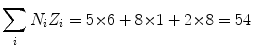
and then using (6.25) to get
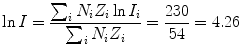
resulting in
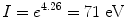
in reasonable agreement with the value of 74 eV that is commonly used for the ionization/excitation potential of Lucite.
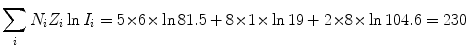
(6.29)
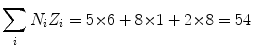
(6.30)
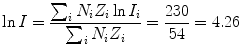
(6.31)
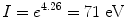
(6.32)
6.4.Q4 (133)
In general, the total stopping power for a given charged particle (CP) is the sum of collision stopping power and radiation stopping power. However, for heavy charged particles the total stopping power is equal to the collision stopping power, since the radiation stopping power for heavy charged particles is negligible in comparison with the collision stopping power.
(a)
Calculate the mass stopping power of water for a proton of kinetic energy E K=100 MeV. Ignore the shell and density corrections. The atomic ionization/excitation potential of water I is 75 eV (see Prob. 132).
(b)
For 1 MeV and 10 MeV protons in water repeat the calculation carried out in (a).
(c)
Calculate the kinetic energy of the deuteron (m d c 2=1875.6 MeV) for which the stopping power of water is the same as that for the proton in (a).
(d)
Calculate the stopping power of water for α particle (m α c 2=3727.3 MeV) having the same velocity as the proton in (a).
(e)
Compare the results obtained in (a) and (b) for protons and in (d) for α particles with data available from the NIST for stopping powers of water for protons and α particles www.nist.gov/pml/data/star/index.cfm.
SOLUTION:
(a) To calculate the mass stopping power of water for a 100 MeV proton we use the Bethe mass collision stopping power equation (T6.42) that reads
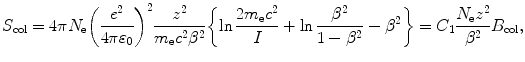
where
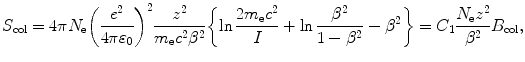
(6.33)
N e
is the electron density (N e=ZN A/A) in number of electrons per gram of absorber medium with Z the atomic number and A the atomic mass of water.
z
is the number of electronic charges on the heavy CP (for proton z=1; for α particle z=2).
β
is velocity of the CP normalized to speed of light c in vacuum.
I
is the mean ionization/excitation potential of water (I=75 eV).
B col
is the so-called atomic stopping number that depends directly on velocity β of the CP and indirectly on the atomic number Z of the absorber (water in our case) through the mean ionization/excitation potential I and is given as
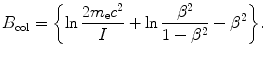
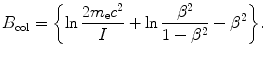
(6.34)
C 1
is a collision stopping power constant independent of absorbing medium as well as of the characteristics of the charged particle. It is expressed as [see (6.18) in Prob. 131]
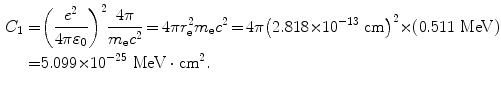
Before we use (6.33) to calculate the stopping power of water, we must determine the electron density N e of water and the velocity β of the 100 MeV proton.
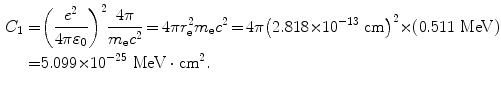
(6.35)
(1) Calculation of electron density N e is carried out as follows: 1 mole of water (H2O) equals to 18.0153 g of water [see (T1.22)] and, by definition, contains 6.022×1023 molecules of water, each molecule containing 2 hydrogen atoms and one oxygen atom. Thus, 1 g of water contains  molecules of water and, since each molecule of water contains 10 electrons, we conclude that the electron density of water N e is
molecules of water and, since each molecule of water contains 10 electrons, we conclude that the electron density of water N e is
![$$ \begin{aligned}[b] N_{\mathrm{e}} &= \frac{1}{18.0153} {\times} \biggl( 6.022 {\times} 10^{23} \frac{\mathrm{molecule}}{\mathrm{g}} \biggr) {\times} \biggl( 10 \frac{\mathrm{electron}}{\mathrm{molecule}} \biggr) \\ &= 3.343 {\times} 10^{23}\ \mathrm{electron}/ \mathrm{g}. \end{aligned} $$](/wp-content/uploads/2016/04/A212719_1_En_6_Chapter_Equ36.gif)
(2) Calculation of 100-MeV-proton velocity β is carried out using the standard expression (T2.7) relating relativistic particle velocity β=υ/c with kinetic energy E K of the particle. The expression is easy to derive from the basic definition of relativistic kinetic energy E K given as follows
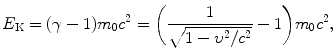
from which we get the following expression for β
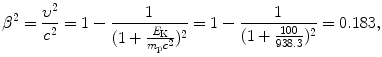
indicating that the velocity υ of a 100 MeV proton is 0.428c.
 molecules of water and, since each molecule of water contains 10 electrons, we conclude that the electron density of water N e is
molecules of water and, since each molecule of water contains 10 electrons, we conclude that the electron density of water N e is![$$ \begin{aligned}[b] N_{\mathrm{e}} &= \frac{1}{18.0153} {\times} \biggl( 6.022 {\times} 10^{23} \frac{\mathrm{molecule}}{\mathrm{g}} \biggr) {\times} \biggl( 10 \frac{\mathrm{electron}}{\mathrm{molecule}} \biggr) \\ &= 3.343 {\times} 10^{23}\ \mathrm{electron}/ \mathrm{g}. \end{aligned} $$](/wp-content/uploads/2016/04/A212719_1_En_6_Chapter_Equ36.gif)
(6.36)
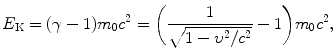
(6.37)
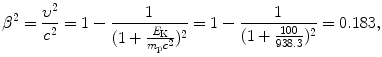
(6.38)
(3) Calculation of the atomic stopping number B col proceeds as follows
![$$ \begin{aligned}[b] B_{\mathrm{col}} &= \biggl\{\ln\frac{2m_{\mathrm{e}}c^2}{I} + \ln \frac{\beta ^2}{1-\beta ^2} - \beta ^2\biggr\} \\ &= \ln\frac{2{\times} 0.511{\times} 10^6~\mathrm{eV}}{75~\mathrm{eV}} + \ln \frac{0.183}{1-0.183} -0.183\\ &= 9.52 + (-1.50) - 0.183 = 7.84. \end{aligned} $$](/wp-content/uploads/2016/04/A212719_1_En_6_Chapter_Equ39.gif)
(4) We now use (6.33) to get the final answer for stopping power of water and 100 MeV protons
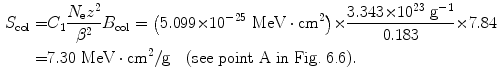
(b) We now repeat, for 1 MeV and 10 MeV protons in water, the calculation carried out in (a), for each energy first calculating β 2 using (6.38) and B col using (6.34) and then using (6.33) to get the final results for the mass stopping power.
![$$ \begin{aligned}[b] B_{\mathrm{col}} &= \biggl\{\ln\frac{2m_{\mathrm{e}}c^2}{I} + \ln \frac{\beta ^2}{1-\beta ^2} - \beta ^2\biggr\} \\ &= \ln\frac{2{\times} 0.511{\times} 10^6~\mathrm{eV}}{75~\mathrm{eV}} + \ln \frac{0.183}{1-0.183} -0.183\\ &= 9.52 + (-1.50) - 0.183 = 7.84. \end{aligned} $$](/wp-content/uploads/2016/04/A212719_1_En_6_Chapter_Equ39.gif)
(6.39)
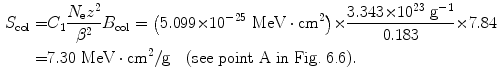
(6.40)
For 1 MeV protons we get the following results for β 2, B col, and S col
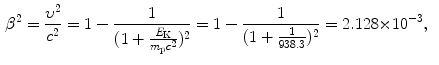
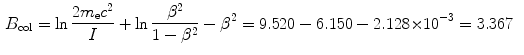
and
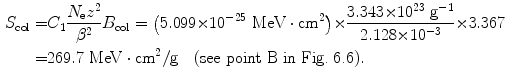
For 10 MeV protons the results are as follows
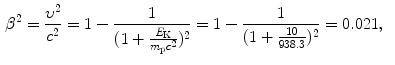
![$$\begin{aligned} &\begin{aligned}[b] B_{\mathrm{col}}(10\ \mathrm{MeV}) &= \ln \frac{2m_{\mathrm{e}}c^{2}}{I} + \ln \frac{\beta ^{2}}{1 - \beta ^{2}} - \beta ^{2} \\ &= 9.520 - 3.842 - 0.021 = 5.657 \end{aligned} \end{aligned}$$](/wp-content/uploads/2016/04/A212719_1_En_6_Chapter_Equ45.gif)
and
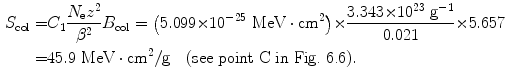
(c) To determine the kinetic energy E K of a deuteron for which the stopping power of water is the same as that for a 100 MeV proton, we take a closer look at the functional dependence of (6.33) on physical properties of the charged particle and note that S col has five components: C 1,N e, z, β, and B col. Of these, C 1, N e, and B col are independent of the charged particle, so that, for the mass stopping power of water to be the same for proton and deuteron, the two charged particles should have the same z (they do, since for both particles z=1) and the same β. As shown in (6.38), β 2=0.183 for a 100 MeV proton, therefore we use (6.37) and determine the deuteron kinetic energy E K that corresponds to β 2=0.183 as follows
![$$ \begin{aligned}[b] E_{\mathrm{K}} &= (\gamma - 1)m_{0}c^{2} = \biggl( \frac{1}{\sqrt{1 - \beta ^{2}}} - 1 \biggr)m_{0}c^{2} \\ &= \biggl( \frac{1}{\sqrt{1 - 0.183}} - 1 \biggr) {\times} (1875.6\ \mathrm{MeV}) \\ &= 199.5\ \mathrm{MeV} \approx 2 \biggl( \frac{1}{\sqrt{1 - \beta ^{2}}} - 1 \biggr)m_{\mathrm{p}}c^{2} = 200\ \mathrm{MeV} .\end{aligned} $$](/wp-content/uploads/2016/04/A212719_1_En_6_Chapter_Equ47.gif)
Thus, for the same stopping power in water, the kinetic energy E K of the charged particle is proportional to the rest energy of the charged particle.
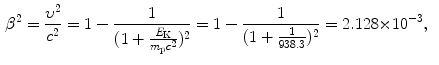
(6.41)
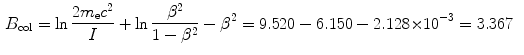
(6.42)
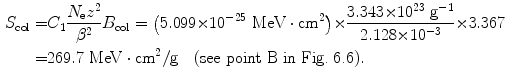
(6.43)
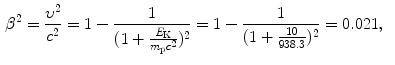
(6.44)
![$$\begin{aligned} &\begin{aligned}[b] B_{\mathrm{col}}(10\ \mathrm{MeV}) &= \ln \frac{2m_{\mathrm{e}}c^{2}}{I} + \ln \frac{\beta ^{2}}{1 - \beta ^{2}} - \beta ^{2} \\ &= 9.520 - 3.842 - 0.021 = 5.657 \end{aligned} \end{aligned}$$](/wp-content/uploads/2016/04/A212719_1_En_6_Chapter_Equ45.gif)
(6.45)
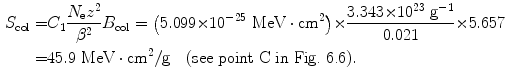
(6.46)
![$$ \begin{aligned}[b] E_{\mathrm{K}} &= (\gamma - 1)m_{0}c^{2} = \biggl( \frac{1}{\sqrt{1 - \beta ^{2}}} - 1 \biggr)m_{0}c^{2} \\ &= \biggl( \frac{1}{\sqrt{1 - 0.183}} - 1 \biggr) {\times} (1875.6\ \mathrm{MeV}) \\ &= 199.5\ \mathrm{MeV} \approx 2 \biggl( \frac{1}{\sqrt{1 - \beta ^{2}}} - 1 \biggr)m_{\mathrm{p}}c^{2} = 200\ \mathrm{MeV} .\end{aligned} $$](/wp-content/uploads/2016/04/A212719_1_En_6_Chapter_Equ47.gif)
(6.47)
Since the rest energy of the deuteron m d c 2 is roughly twice the rest energy m p c 2 of the proton, its kinetic energy E K for the same velocity β is twice as high. Thus, the mass stopping power of water is the same (7.30 MeV⋅cm2/g) for a 100 MeV proton and a 200 MeV deuteron because both charged particles have the same velocity β as well as the same atomic number z=1.
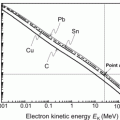
(d) To calculate the stopping power of water for α particle having the same velocity as the proton, we again evaluate the functional dependence of (6.33) and note that, in addition to charged particle velocity β, the mass stopping power also depends on the square of the atomic number z. Since z=2 for α particle compared to z=1 for proton, we conclude that the mass stopping power of water is 4 times as large (4×7.30 MeV⋅cm2/g=29.2 MeV⋅cm2/g) for α particle as that for proton at the same velocity β of the two particles (see point D in Fig. 6.6).
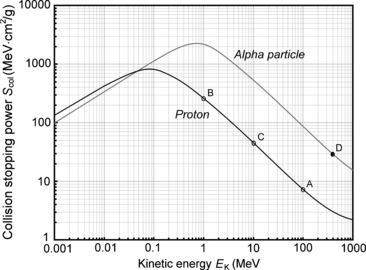

Fig. 6.6
Collision stopping power of water for proton and α particle in the kinetic energy range from 1 keV to 1 GeV. The continuous curves are data from the NIST, the four data points are results of our calculations of stopping power with the Bethe stopping power equation (6.33) that ignores the shell correction and the density correction
From the discussion in (c) we also note that, at same velocity β, kinetic energy E K(α) of an α particle is approximately 4-times as large as that of a proton
![$$ \begin{aligned}[b] E_{\mathrm{K}}(\alpha ) &= (\gamma - 1)m_{\alpha} c^{2} = \biggl( \frac{1}{\sqrt{1 - \beta ^{2}}} \biggr)m_{\alpha} c^{2} \\ &= \biggl( \frac{1}{\sqrt{1 - 0.183}} \biggr) {\times} (3727.3\ \mathrm{MeV}) = 396.4\ \mathrm{MeV}. \end{aligned} $$](/wp-content/uploads/2016/04/A212719_1_En_6_Chapter_Equ48.gif)
(e) For 1 MeV, 10 MeV, and 100 MeV protons we calculated with Bethe equation (6.33) the following stopping powers of water: 269.7 MeV⋅cm2/g, 45.9 MeV⋅cm2/g, and 7.30 MeV⋅cm2/g, respectively, while the NIST, accounting for all known corrections, gives the following respective results: 260.8 MeV⋅cm2/g, 45.7 MeV⋅cm2/g, and 7.29 MeV⋅cm2/g. For an α particle with kinetic energy E K(α)=400 MeV the NIST provides a stopping power of water of 29.2 MeV⋅cm2/g, while our rudimentary calculation yields 29.2 MeV⋅cm2/g. Thus, the agreement with the basic Bethe equation (6.33) and the one incorporating all currently known corrections is quite good.
![$$ \begin{aligned}[b] E_{\mathrm{K}}(\alpha ) &= (\gamma - 1)m_{\alpha} c^{2} = \biggl( \frac{1}{\sqrt{1 - \beta ^{2}}} \biggr)m_{\alpha} c^{2} \\ &= \biggl( \frac{1}{\sqrt{1 - 0.183}} \biggr) {\times} (3727.3\ \mathrm{MeV}) = 396.4\ \mathrm{MeV}. \end{aligned} $$](/wp-content/uploads/2016/04/A212719_1_En_6_Chapter_Equ48.gif)
(6.48)
Stopping power of water for proton and α particle available from the NIST is shown in Fig. 6.6 in the energy range from 1 keV to 1000 MeV and our calculated results are superimposed on the graph with data points. The good agreement between our calculation and the NIST data is evident.
6.4.Q5 (134)
Bethe equation for mass collision stopping power S col of a stopping medium (absorber) for heavy charged particles (CP) is given as
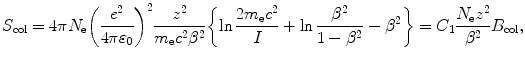
with parameters defined in Prob. 131 and the Fano shell and density corrections neglected.
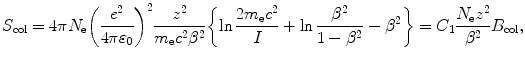
(6.49)
(a)
Determine the mass collision stopping power S col of water for a proton with incident kinetic energy E K=51 MeV. Mean ionization/excitation potential I of water is 75 eV; electron density N e=ZN A/A was determined in Prob. 133 as N e=3.343×1023 el/g.
(b)
Determine the incident kinetic energy E K of a deuteron for which water has the same mass collision stopping power S col as for the proton in (a).
(c)
Determine the incident kinetic energy E K and mass collision stopping power S col of water for the following particles: α particle, carbon-6 ion, and neon-10 ion having the same incident velocity β=υ/c as the proton in (a) and deuteron in (b).
SOLUTION:
(a) To use (6.49) for calculation of S col of water we will need the following parameters: (1) constant C 1, (2) velocity β=υ/c of proton with E K=51 MeV, and (3) collision stopping number of water for 51 MeV proton.
(1) From (6.18) in Prob. 131 we get the following expression for constant C 1
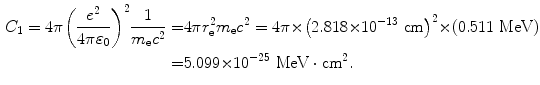
(2) Velocity of the 51-MeV-proton is determined from the standard expression for relativistic kinetic energy E K as follows
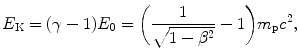
from where it follows that
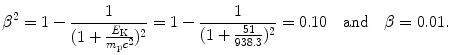
(3) Atomic stopping number B col of proton in water is determined as follows
![$$ \begin{aligned}[b] B_{\mathrm{col}} &= \biggl\{ \ln \frac{2m_{\mathrm{e}}c^{2}}{I} + \ln \frac{\beta ^{2}}{1 - \beta ^{2}} - \beta ^{2} \biggr\} \\ &= \ln \frac{2 {\times} 0.511 {\times} 10^{6}\ \mathrm{eV}}{75\ \mathrm{eV}} + \ln \frac{0.1}{0.9} - 0.1 = 9.52 - 2.197 - 0.10 = 7.22. \end{aligned} $$](/wp-content/uploads/2016/04/A212719_1_En_6_Chapter_Equ53.gif)
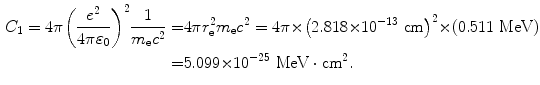
(6.50)
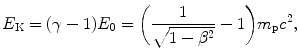
(6.51)
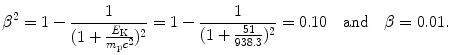
(6.52)
![$$ \begin{aligned}[b] B_{\mathrm{col}} &= \biggl\{ \ln \frac{2m_{\mathrm{e}}c^{2}}{I} + \ln \frac{\beta ^{2}}{1 - \beta ^{2}} - \beta ^{2} \biggr\} \\ &= \ln \frac{2 {\times} 0.511 {\times} 10^{6}\ \mathrm{eV}}{75\ \mathrm{eV}} + \ln \frac{0.1}{0.9} - 0.1 = 9.52 - 2.197 - 0.10 = 7.22. \end{aligned} $$](/wp-content/uploads/2016/04/A212719_1_En_6_Chapter_Equ53.gif)
(6.53)
Now that we have all the required parameters we can determine S col as follows
![$$ \begin{aligned}[b] S_{\mathrm{col}} &= C_{1}\frac{N_{\mathrm{e}}z^{2}}{\beta ^{2}}B_{\mathrm{col}} = \bigl(5.099 {\times} 10^{ - 25}\ \mathrm{MeV} \cdot \mathrm{cm}^{2} \bigr) {\times} \frac{3.343 {\times} 10^{23}}{0.1\ \mathrm{g}} {\times} 7.22 \\ &= 12.31 \frac{\mathrm{MeV} \cdot \mathrm{cm}^{2}}{\mathrm{g}} \end{aligned} $$](/wp-content/uploads/2016/04/A212719_1_En_6_Chapter_Equ54.gif)
and get a result that is in excellent agreement with the NIST mass collision stopping power S col of 12.25 MeV⋅cm2/g obtained for a 51 MeV proton.
![$$ \begin{aligned}[b] S_{\mathrm{col}} &= C_{1}\frac{N_{\mathrm{e}}z^{2}}{\beta ^{2}}B_{\mathrm{col}} = \bigl(5.099 {\times} 10^{ - 25}\ \mathrm{MeV} \cdot \mathrm{cm}^{2} \bigr) {\times} \frac{3.343 {\times} 10^{23}}{0.1\ \mathrm{g}} {\times} 7.22 \\ &= 12.31 \frac{\mathrm{MeV} \cdot \mathrm{cm}^{2}}{\mathrm{g}} \end{aligned} $$](/wp-content/uploads/2016/04/A212719_1_En_6_Chapter_Equ54.gif)
(6.54)
(b) For a heavy CP to engender in absorber the same mass collision stopping power S col as does a proton, it must have the same velocity β as well as the same charge number z=1. Since for both proton and deuteron z=1, for a deuteron to engender S col of 12.31 MeV⋅cm2/g in water, it must have the same velocity β of 0.01 as does a 51 MeV proton. Since the deuteron is heavier than the proton, its kinetic energy E K(d) must be higher than that of the proton E K(p). The ratio E K(d)/E K(p) is determined from (6.51) as follows
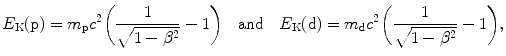
from where it follows that the ratio E K(d)/E K(p) is given as follows
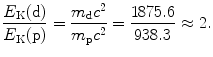
Thus, for a deuteron to engender the same stopping power in water as does a proton, it must have the same velocity as the proton, and this implies that it has a kinetic energy that is twice the kinetic energy of the proton. Mass collision stopping power S col of water is therefore 12.31 MeV⋅cm2/g for 51 MeV proton as well as for 102 MeV deuteron.
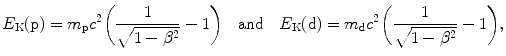
(6.55)
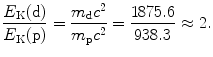
(6.56)
(c) We now calculate: (1) kinetic energy E K(m 0) of particle with rest mass m 0 and (2) mass collision stopping power S col of water for various CPs (deuteron, α particle, carbon-6 ion, and neon-10 ion), all of velocity β=0.01, as determined for 51 MeV proton in (a).
(1)
Kinetic energy E K(m 0) of heavy CPs that all have the same velocity β is linearly proportional to CP’s rest energy E 0=m 0 c 2. Based on (6.56) we reach a general conclusion that kinetic energy of a given heavy CP of rest mass m 0 can be expressed in terms of kinetic energy of proton of rest mass m p as
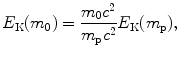
provided that both CPs have the same velocity β. Kinetic energy E K(m 0) for proton, deuteron, α particle, carbon-6 ion, and neon-10 ion, all traveling with velocity β=0.01, determined from (6.57) is listed in row (4) of Table 6.8, while kinetic energy of the various CPs stated in MeV/u is listed in row (5) of the table. It is evident that CPs with same MeV/u have the same velocity β and engender the same stopping number B col in a given stopping material.
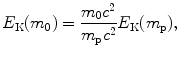
(6.57)
Table 6.8
Various parameters in calculation of kinetic energy E K and mass stopping power of water for various heavy CPs (proton, deuteron, α particle, carbon-6 ion, and neon-10 ion)
1 | Particle | Proton | Deuteron | α particle | Carbon-6 | Neon-10 |
|---|---|---|---|---|---|---|
2 | E 0=m 0 c 2 | 938.3 | 1875.6 | 3727.3 | 11174.9 | 18617.7 |
3 | m 0 c 2/m p c 2 | 1.0 | 2 | 3.97 | 11.91 | 19.84 |
4 | E K(m 0) | 51 | 102 | 202.5 | 11175 | 18616 |
5 | E K/A (MeV/u) | 51 | ∼51 | ∼51 | ∼51 | ∼51 |
6 | z | 1 | 1 | 2 | 6 | 10 |
7 | S col(m 0,z) (MeV⋅cm2/g) | 12.31 | 12.31 | 49.2 | 443.2 | 1231 |
(2)
Mass collision stopping power S col(m 0,z) for the various CPs of rest mass m 0, all with the same velocity β=0.01, will now be expressed in terms of S col(m p,z) of water for a proton. From (6.49) it is evident that, for a constant velocity β, S col(m 0,z) is linearly proportional with z 2, where z is the number of charges that the CP carries, i.e.,
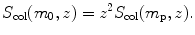
Results for S col(m 0,z) of water for proton, deuteron, α particle, carbon-6 ion, and neon-10 ion are summarized in row (7) of Table 6.8. Note that our S col of water for α particles of E K=202.5 MeV is in excellent agreement with the NIST value of S col=49.03 MeV⋅cm2/g for the same conditions.
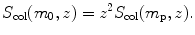
(6.58)
6.4.Q6 (135)
Specific ionization j is defined as the number of primary and secondary ion pairs produced per unit length of the path traced by a charged particle (CP) traversing an absorber. It is usually expressed in ion pairs per millimeter (ip/mm) and increases with the charge of the CP. The specific ionization produced in the absorber by a CP at a given kinetic energy E K is proportional to the linear stopping power s of the absorber and the proportionality constant (at least for gases) is 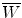 , the mean energy required to produce an ion pair in the absorber at particle energy E K. For gases
, the mean energy required to produce an ion pair in the absorber at particle energy E K. For gases 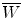 is essentially independent of particle energy and only slightly depends on the CP type. For example,
is essentially independent of particle energy and only slightly depends on the CP type. For example, 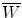 of air is
of air is 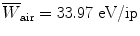 for electrons and x rays, 35 eV/ip for protons, and 36 eV/ip for α particles.
for electrons and x rays, 35 eV/ip for protons, and 36 eV/ip for α particles.
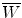 , the mean energy required to produce an ion pair in the absorber at particle energy E K. For gases
, the mean energy required to produce an ion pair in the absorber at particle energy E K. For gases 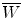 is essentially independent of particle energy and only slightly depends on the CP type. For example,
is essentially independent of particle energy and only slightly depends on the CP type. For example, 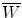 of air is
of air is 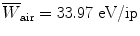 for electrons and x rays, 35 eV/ip for protons, and 36 eV/ip for α particles.
for electrons and x rays, 35 eV/ip for protons, and 36 eV/ip for α particles.(a)
Determine the specific ionization j resulting from the passage of a 10 MeV proton through standard air (T=0 °C and p=101.3 kPa). Density of standard air ρ air=1.293×10−3 g/cm3; the mean ionization/excitation potential of air is I air=86 eV. Ignore the Fano shell and density corrections in the calculation of collision stopping powers.
(b)
Based on Fig. 6.7 that shows the mass collision stopping power S col of standard air against proton kinetic energy E K in the kinetic energy range from 10−3 MeV to 104 MeV, determine the maximum possible specific ionization j in standard air for protons. Stopping power data are from the NIST at http://physics.nist.gov/cgi-bin/Star/ap_table.pl.
(c)
Based on data from the NIST, given in Table 6.9A, prepare a plot of specific ionization j against residual range R residual for a 10 MeV proton in standard air. In order to get a clear picture of the Bragg peak plot j only for the last 5 mm of the proton path in air.
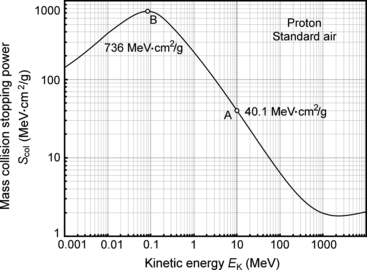
Fig. 6.7
Mass collision stopping power S col of standard air against kinetic energy E K of proton. Point A highlights S col of standard air for a 10 MeV proton calculated in (a); point B highlights the maximum that occurs at 0.084 MeV and is used in calculation of the maximum specific ionization
Table 6.9A
Mass collision stopping power S col and CSDA range R CSDA for protons in air in the kinetic energy E K range from 0 to 10 MeV. The table is to be used to determine a plot of specific ionization against residual range for 10 MeV protons in standard air where E K is kinetic energy of the proton propagating in standard air, S col is mass collision stopping power of standard air, s col is linear collision stopping power of standard air, j is specific ionization produced in standard air by protons of energy E K, R CSDA is the continuous slowing down approximation (CSDA) range in g/cm2 for protons of energy E K in standard air, r CSDA is the CSDA range in mm of air for protons of energy E K
1 | E K (MeV) | S col a (MeV⋅cm2/g) | s col (MeV/cm) | j (i.p./mm) | R CSDA a (g/cm2) | R residual (mm) |
|---|---|---|---|---|---|---|
2 | 0.001 | 141.4 | 9.857×10−6 | |||
3 | 0.005 | 277.6 | 2.891×10−5 | |||
4 | 0.01 | 385.0 | 4.400×10−5 | |||
5 | 0.05 | 689.7 | 1.152×10−4 | |||
6 | 0.07 | 729.3 | 1.433×10−4 | |||
7 | 0.08 | 735.5 | 1.569×10−4 | |||
8 | 0.09 | 735.2 | 1.705×10−4 | |||
9 | 0.2 | 592.8 | 3.349×10−4 | |||
10 | 0.5 | 350.1 | 1.021×10−3 | |||
11 | 1 | 222.9 | 2.867×10−3 | |||
12 | 2 | 137.1 | 8.792×10−3 | |||
13 | 5 | 69.1 | 4.173×10−2 | |||
14 | 10 | 40.1 | 1.408×10−1 |