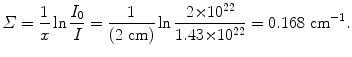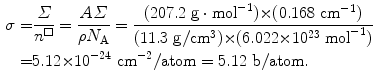(1)
Faculty of Medicine, Department, of Oncology and Medical Physics Unit, McGill University, Montreal, Québec, Canada
Abstract
Chapter 9 consists of 13 problems covering 6 sections that deal with various aspects of neutron interactions with matter. Neutrons, by virtue of their neutrality, are considered indirectly ionizing radiation that exhibits a quasi exponential penetration into the absorber and deposits energy in an absorber through a two-step process: (1) energy transfer to heavy charged particles and (2) energy deposition in the absorber through Coulomb interactions of these charged particles with atoms of the absorber. As they penetrate into the absorber, neutrons may undergo elastic and inelastic scattering as well as trigger nuclear reactions, such as neutron capture, spallation, and fission.
Two distinct categories of neutron are of direct importance in medical physics: (1) thermal neutrons used in boron neutron capture therapy (BNCT) and (2) fast neutrons used in external beam radiotherapy. Indirectly, thermal neutrons also play an important role in production of radionuclide sources for use in external beam radiotherapy, in remote afterloading brachytherapy, and nuclear medicine imaging. A nuclear reactor and two types of thermal neutron interaction are used for production of radioactive sources: (1) neutron activation of suitable target material and (2) fission reaction induced by thermal neutron in fissile target material.
Section 9.1 presents long questions on general aspects of neutron interactions with absorber nuclei and Sect. 9.2 deals with various processes by which neutrons interact with nuclei of the absorber, such as elastic, inelastic, and non-elastic scattering as well as neutron capture, spallation, and fission.
Section 9.3 presents a problem on neutron kerma and Sect. 9.4 presents a problem on the neutron kerma factor. Section 9.5 introduces two problems on neutron dose deposition in tissue by thermal neutrons, intermediate neutrons, and fast neutrons. The last section (Sect. 9.6) provides problems on the use of neutrons in medicine either (1) for boron neutron capture therapy (BNCT), (2) production of fast neutron beams for radiotherapy, or (3) use of neutron emitters in brachytherapy.
Chapter 9 consists of 13 problems covering 6 sections that deal with various aspects of neutron interactions with matter. Neutrons, by virtue of their neutrality, are considered indirectly ionizing radiation that exhibits a quasi exponential penetration into the absorber and deposits energy in an absorber through a two-step process: (1) energy transfer to heavy charged particles and (2) energy deposition in the absorber through Coulomb interactions of these charged particles with atoms of the absorber. As they penetrate into the absorber, neutrons may undergo elastic and inelastic scattering as well as trigger nuclear reactions, such as neutron capture, spallation, and fission.
Two distinct categories of neutron are of direct importance in medical physics: (1) thermal neutrons used in boron neutron capture therapy (BNCT) and (2) fast neutrons used in external beam radiotherapy. Indirectly, thermal neutrons also play an important role in production of radionuclide sources for use in external beam radiotherapy, in remote afterloading brachytherapy, and nuclear medicine imaging. A nuclear reactor and two types of thermal neutron interaction are used for production of radioactive sources: (1) neutron activation of suitable target material and (2) fission reaction induced by thermal neutron in fissile target material.
Section 9.1 presents long questions on general aspects of neutron interactions with absorber nuclei and Sect. 9.2 deals with various processes by which neutrons interact with nuclei of the absorber, such as elastic, inelastic, and non-elastic scattering as well as neutron capture, spallation, and fission.
Section 9.3 presents a problem on neutron kerma and Sect. 9.4 presents a problem on the neutron kerma factor. Section 9.5 introduces two problems on neutron dose deposition in tissue by thermal neutrons, intermediate neutrons, and fast neutrons. The last section (Sect. 9.6) provides problems on the use of neutrons in medicine either (1) for boron neutron capture therapy (BNCT), (2) production of fast neutron beams for radiotherapy, or (3) use of neutron emitters in brachytherapy.
9.1 General Aspects of Neutron Interactions with Absorbers
9.1.Q1 (198)
Neutrons, like photons, belong to the category of indirectly ionizing radiation. Used in science, industry, and medicine, they come in a wide spectrum of kinetic energy 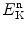 , ranging from 10−8 eV for ultra-cold neutrons up to few GeV for relativistic cosmic neutrons. Neutrons transfer energy to absorbing medium through an intermediate step in which energy is transferred from the neutron to a charged particle which in turn transfers energy to the absorber medium through Coulomb interactions between the liberated charged particle and orbital electrons of the absorber. Thus, energy deposition in absorber by a neutron beam occurs through secondary charged particles, such as protons, α-particles, and recoiling nuclei. As they penetrate into absorbing medium, neutrons may undergo elastic, inelastic, or non-elastic scattering or they may trigger nuclear reactions, such as neutron capture, spallation, and fission.
, ranging from 10−8 eV for ultra-cold neutrons up to few GeV for relativistic cosmic neutrons. Neutrons transfer energy to absorbing medium through an intermediate step in which energy is transferred from the neutron to a charged particle which in turn transfers energy to the absorber medium through Coulomb interactions between the liberated charged particle and orbital electrons of the absorber. Thus, energy deposition in absorber by a neutron beam occurs through secondary charged particles, such as protons, α-particles, and recoiling nuclei. As they penetrate into absorbing medium, neutrons may undergo elastic, inelastic, or non-elastic scattering or they may trigger nuclear reactions, such as neutron capture, spallation, and fission.
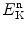 , ranging from 10−8 eV for ultra-cold neutrons up to few GeV for relativistic cosmic neutrons. Neutrons transfer energy to absorbing medium through an intermediate step in which energy is transferred from the neutron to a charged particle which in turn transfers energy to the absorber medium through Coulomb interactions between the liberated charged particle and orbital electrons of the absorber. Thus, energy deposition in absorber by a neutron beam occurs through secondary charged particles, such as protons, α-particles, and recoiling nuclei. As they penetrate into absorbing medium, neutrons may undergo elastic, inelastic, or non-elastic scattering or they may trigger nuclear reactions, such as neutron capture, spallation, and fission.
, ranging from 10−8 eV for ultra-cold neutrons up to few GeV for relativistic cosmic neutrons. Neutrons transfer energy to absorbing medium through an intermediate step in which energy is transferred from the neutron to a charged particle which in turn transfers energy to the absorber medium through Coulomb interactions between the liberated charged particle and orbital electrons of the absorber. Thus, energy deposition in absorber by a neutron beam occurs through secondary charged particles, such as protons, α-particles, and recoiling nuclei. As they penetrate into absorbing medium, neutrons may undergo elastic, inelastic, or non-elastic scattering or they may trigger nuclear reactions, such as neutron capture, spallation, and fission.Two distinct categories of neutrons are of direct importance in medical physics:
Indirectly, thermal neutrons play an important role in production of radionuclide sources that are used in external beam radiotherapy, brachytherapy, and nuclear medicine imaging. In neutron dosimetry three regions of neutron kinetic energy are of importance: thermal, intermediate, and fast neutron region.
(1)
Thermal neutrons used in boron-neutron capture therapy (BNCT).
(2)
Fast neutrons used in external beam radiotherapy and brachytherapy.
(a)
Discuss the basic properties of neutrons relevant to the use of neutrons in medicine for diagnosis (imaging) and therapy (radiotherapy) of disease.
(b)
Calculate the velocity of neutrons with kinetic energy E K of 10−7 eV (ultra-cold neutron), 10−4 eV (cold neutron), 0.025 eV (thermal neutron), 1 MeV (fast neutron), 14.1 MeV (fast neutron from d-t reaction), 100 MeV (cosmic neutron) and 1 GeV (cosmic neutron).
SOLUTION:
(a) Basic properties of neutrons with emphasis on use in medicine.
(b) Velocity of a neutron with a given kinetic energy E K and rest energy m n c 2=939.6 MeV is calculated from the classical expression for kinetic energy (T2.5)
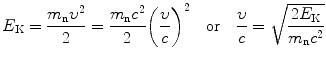
for relatively slow neutrons with velocity υ<0.01c and from the relativistic expression for E K (T2.7)
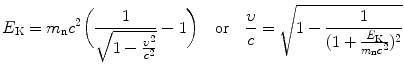
for fast neutrons with velocity υ>0.01c.
(1)
Neutron is a subatomic particle in the family of hadrons, composed of three quarks and exhibiting strong interaction with other hadrons.
(2)
Ernest Rutherford in 1920 postulated the existence of the neutron and William Chadwick in 1932 discovered it at the University of Cambridge in the U.K.
(3)
The symbol for the neutron is n or n0. It possesses no electric charge and its rest mass m n is slightly larger than that of the proton.
Rest mass of neutron: m n=939.6 MeV/c 2; rest mass of proton: m p=938.3 MeV/c 2.
(4)
Neutron is stable when it is bound in atomic nucleus; however, a free (extra-nuclear) neutron is unstable (radioactive) and decays through β − decay into a proton, electron, and electronic antineutrino (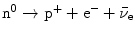 ) with a mean lifetime τ≈14.9 min or half-life t 1/2=τln2≈10.3 min. In unstable nuclei that harbor an excess number of neutrons, neutron can also decay through β − decay, however, the half life of this β − decay is a characteristic of the decaying nucleus and different from that of the free neutron.
) with a mean lifetime τ≈14.9 min or half-life t 1/2=τln2≈10.3 min. In unstable nuclei that harbor an excess number of neutrons, neutron can also decay through β − decay, however, the half life of this β − decay is a characteristic of the decaying nucleus and different from that of the free neutron.
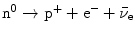 ) with a mean lifetime τ≈14.9 min or half-life t 1/2=τln2≈10.3 min. In unstable nuclei that harbor an excess number of neutrons, neutron can also decay through β − decay, however, the half life of this β − decay is a characteristic of the decaying nucleus and different from that of the free neutron.
) with a mean lifetime τ≈14.9 min or half-life t 1/2=τln2≈10.3 min. In unstable nuclei that harbor an excess number of neutrons, neutron can also decay through β − decay, however, the half life of this β − decay is a characteristic of the decaying nucleus and different from that of the free neutron.(5)
Free neutrons easily pass through atoms, because they have no electrical charge, thereby forming highly penetrating, indirectly ionizing, radiation beams that interact with matter only through direct collisions with nuclei of absorber atoms. Interactions of neutrons with orbital electrons of absorber atoms are generally not of any importance and are thus ignored.
(6)
Neutron detection is more complex than detection of directly ionizing charged particles and indirectly ionizing photons. Most common methods for detection of neutrons rely on neutron capture (neutron absorption) by the nucleus of an absorber atom or on elastic scattering of neutrons off nuclei of absorber.
(7)
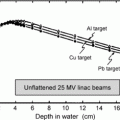
The secondary charged particles released by fast neutrons in the absorbing medium produce a dose build-up similar to that that occurs in megavoltage photon beams. The depth of dose maximum z max of a clinical fast neutron beam depends on the energy and spectrum of the beam and for a source-surface distance of 100 cm and field size of 10×10 cm2 is of the order from 0.5 cm to 1.5 cm. Beyond z max there is a continuous quasi-exponential fall-off in the dose with increasing depth in water as a result of:
In contrast to megavoltage x-ray beams, the field size of neutron beams has a significant effect on depth dose characteristics because of the high probability for neutron scattering within the neutron beam.
(i)
Attenuation of the neutron beam by absorbing medium (water).
(ii)
Increase in distance from the source (inverse square law).
(8)
Fast neutron beams are significantly more complex and more expensive to use in radiotherapy than are megavoltage x-ray beams, yet, from a physics point-of-view, they produce no better dose distributions than do megavoltage x-ray beams. However, from a radiobiological point-of-view, fast neutrons offer a distinct advantage over megavoltage x-ray beams because of the so-called oxygen enhancement ratio (OER) which amounts to 3 for x rays while it is much closer to 1 for fast neutron beams.
It turns out that the presence of oxygen in a cell acts as a radiosensitizer, making radiation more damaging for a given delivered dose. Since tumor cells are typically poorly oxygenated (tumor hypoxia) in comparison to normal cells, a given dose of x rays causes more damage to well oxygenated normal cells than to hypoxic tumor cells. Thus, in comparison to normal tissue, the oxygen effect decreases the sensitivity of tumor tissue to megavoltage x rays and decreases the tumor control probability. It is generally believed that fast neutron irradiation overcomes this effect, because the OER of fast neutrons is much smaller than that of megavoltage x rays.
(9)
For use in radiotherapy, neutron beams are produced either with a cyclotron or a neutron generator. In a cyclotron protons or deuterons are accelerated to kinetic energies of 50 MeV to 80 MeV and strike a thick beryllium target to produce fast neutrons that are collimated into a clinical neutron beam. The neutron beam produced with a beryllium target has beam penetration and build-up characteristics similar to those of 4 MV to 10 MV megavoltage x-ray beams. In a neutron generator deuterons (d) are accelerated to 250 keV and strike a tritium (t) target to produce a 14.1 MeV neutron beam with depth dose characteristics similar to those obtained for a cobalt-60 teletherapy γ-ray beam.
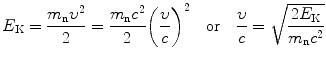
(9.1)
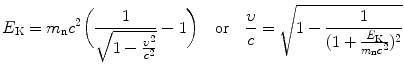
(9.2)
Results of our neutron velocity calculations are displayed in Table 9.1 and plotted in Fig. 9.1 in the form of log υ/c against log E K which appears to follow a power function of exponent 1/2 [classical expression (9.1)], except for saturation occurring at very high (relativistic) kinetic energies where (9.2) must be used and (9.1) is no longer applicable.
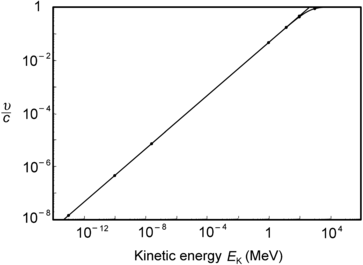

Fig. 9.1
Normalized velocity υ/c against neutron kinetic energy E K
Table 9.1
Results of calculation of neutron velocity υ against kinetic energy E K for neutrons ranging in kinetic energy from 10−7 eV to 1 GeV. Velocities in bold face are calculated with the relativistic equation (9.2) while velocities in standard font are calculated for comparison purposes with the classical equation (9.1)
(1) | Neutron | Kinetic energy E K |  (classical) (classical) | 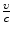 (relativistic) (relativistic) | 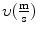 |
|---|---|---|---|---|---|
(2) | Ultra-cold | 10−7 eV | 1.46×10 −8 | – | 4.4 |
(3) | Cold | 10−4 eV | 4.61×10 −7 | – | 138.4 |
(4) | Thermal | 0.025 eV | 7.29×10 −6 | – | ∼2200 |
(5) | Fast | 1 MeV | 0.04614 | 0.04610 | ∼1.38×107 |
(6) | Fast | 14.1 MeV | 0.1732 | 0.1713 | ∼5.14×107 |
(7) | Cosmic | 100 MeV | 0.4614 | 0.4279 | ∼1.28×108 |
(8) | Cosmic | 1 GeV | – | 0.8748 | ∼2.62×108 |
9.1.Q2 (199)
Neutrons are classified, similarly to x rays and γ rays, as indirectly ionizing radiation that deposits energy in absorbing medium through an intermediate step involving release of secondary charged particles in the attenuating medium. Whereas photons interact with atomic electrons and release electrons and positrons in the attenuating medium, neutrons interact with nuclei of the attenuator and release nuclear particles, such as protons, deuterons, α particles, and heavier nuclear recoils.
(a)
Define neutron fluence φ and neutron fluence rate (neutron flux density) 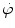 .
.
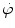 .
.(b)
Define total microscopic neutron cross section σ and total macroscopic cross section Σ.
(c)
Describe attenuation of a collimated neutron beam in attenuating medium.
(d)
Define the mean free path Λ of neutrons and reaction rate 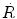 of neutrons.
of neutrons.
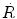 of neutrons.
of neutrons.(e)
A lead attenuator (atomic number Z=82, mass density ρ=11.3 g/cm3, atomic weight A=207.2 g/mol) of thickness z=2 cm attenuates a collimated neutron beam of kinetic energy 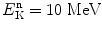 from neutron fluence rate
from neutron fluence rate 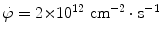 to a fluence rate of
to a fluence rate of 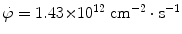 . For this neutron beam interacting with lead attenuator calculate:
. For this neutron beam interacting with lead attenuator calculate:
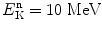 from neutron fluence rate
from neutron fluence rate 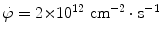 to a fluence rate of
to a fluence rate of 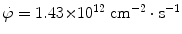 . For this neutron beam interacting with lead attenuator calculate:
. For this neutron beam interacting with lead attenuator calculate:(1)
Total macroscopic cross section Σ.
(2)
Total microscopic cross section σ.
(3)
Mean free path Λ.
(4)
Neutron reaction rate 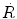 at a depth of 1 cm in lead attenuator.
at a depth of 1 cm in lead attenuator.
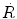 at a depth of 1 cm in lead attenuator.
at a depth of 1 cm in lead attenuator.SOLUTION:
(a) Neutron fluence φ and neutron fluence rate 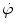 are two basic physical quantities used for describing neutron beams and neutron fields. A neutron radiation field is established by neutron sources in conjunction with an attenuating medium that causes absorption as well as scattering of neutrons.
are two basic physical quantities used for describing neutron beams and neutron fields. A neutron radiation field is established by neutron sources in conjunction with an attenuating medium that causes absorption as well as scattering of neutrons.
Typical unit of neutron fluence φ is cm−2, expressing number of neutrons per cm2. Typical unit of neutron fluence rate or flux density 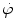 is cm−2⋅s−1, expressing number of neutrons per cm2 per second.
is cm−2⋅s−1, expressing number of neutrons per cm2 per second.
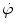 are two basic physical quantities used for describing neutron beams and neutron fields. A neutron radiation field is established by neutron sources in conjunction with an attenuating medium that causes absorption as well as scattering of neutrons.
are two basic physical quantities used for describing neutron beams and neutron fields. A neutron radiation field is established by neutron sources in conjunction with an attenuating medium that causes absorption as well as scattering of neutrons.(1)
Neutron fluence φ, according to the ICRU, is defined as the quotient of ΔN by Δa or φ=ΔN/Δa, with ΔN the number of particles that enter a sphere of cross sectional area Δa.
(2)
Neutron fluence rate or neutron flux density 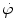 , in addition to neutron kinetic energy E K, is a convenient parameter used for describing the presence of free neutrons in an attenuating medium. Several closely related definitions of neutron fluence rate (neutron flux) are in use:
, in addition to neutron kinetic energy E K, is a convenient parameter used for describing the presence of free neutrons in an attenuating medium. Several closely related definitions of neutron fluence rate (neutron flux) are in use:
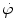 , in addition to neutron kinetic energy E K, is a convenient parameter used for describing the presence of free neutrons in an attenuating medium. Several closely related definitions of neutron fluence rate (neutron flux) are in use:
, in addition to neutron kinetic energy E K, is a convenient parameter used for describing the presence of free neutrons in an attenuating medium. Several closely related definitions of neutron fluence rate (neutron flux) are in use:(i)
According to the ICRU, neutron fluence rate 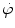 is the quotient of Δφ by Δt where Δφ is the increment of neutron fluence in the time interval Δt;
is the quotient of Δφ by Δt where Δφ is the increment of neutron fluence in the time interval Δt;
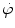 is the quotient of Δφ by Δt where Δφ is the increment of neutron fluence in the time interval Δt;
is the quotient of Δφ by Δt where Δφ is the increment of neutron fluence in the time interval Δt;(ii)
Fluence rate 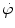 is also defined as the number of neutrons passing through a particular cross sectional area in any direction per unit time; and
is also defined as the number of neutrons passing through a particular cross sectional area in any direction per unit time; and
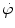 is also defined as the number of neutrons passing through a particular cross sectional area in any direction per unit time; and
is also defined as the number of neutrons passing through a particular cross sectional area in any direction per unit time; and(iii)
Fluence rate 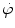 is the product of neutron velocity υ and neutron density (number of free neutrons per unit volume of the attenuator) n given as
is the product of neutron velocity υ and neutron density (number of free neutrons per unit volume of the attenuator) n given as 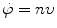 .
.
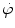 is the product of neutron velocity υ and neutron density (number of free neutrons per unit volume of the attenuator) n given as
is the product of neutron velocity υ and neutron density (number of free neutrons per unit volume of the attenuator) n given as 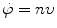 .
.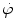 is cm−2⋅s−1, expressing number of neutrons per cm2 per second.
is cm−2⋅s−1, expressing number of neutrons per cm2 per second.(b) Neutrons being uncharged particles interact with nuclei of attenuating media through direct collisions rather than via Coulomb interactions. Many modes of interaction between incident neutron and nuclei of attenuating medium are available to a neutron propagating through an attenuating medium.
(c) Just as the linear attenuation coefficient μ is used for description of photon beam attenuation in attenuating medium, so is the macroscopic cross section Σ used for describing attenuation of collimated neutron beams in attenuating medium. The decrease in beam intensity dI is proportional to the neutron beam intensity I, microscopic cross section σ of the attenuator, atomic density n □ of attenuator, and thickness dx of the attenuating medium
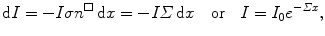
where Σ is the macroscopic cross section of the attenuating medium for neutrons with kinetic energy 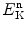 .
.
(1)
Total microscopic cross sections. The probability of a given type of interaction i is expressed in terms of a microscopic cross section σ i for the given target nucleus. For a given target nucleus and a given neutron kinetic energy 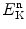 a set of partial microscopic cross sections σ i is usually available for the various possible interaction modes i. At a given
a set of partial microscopic cross sections σ i is usually available for the various possible interaction modes i. At a given 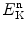 and target nucleus, the sum ∑ i σ i is referred to as the total microscopic cross section σ. Units of microscopic cross sections are cm2/atom, m2/atom, and barns per atom (b/atom).
and target nucleus, the sum ∑ i σ i is referred to as the total microscopic cross section σ. Units of microscopic cross sections are cm2/atom, m2/atom, and barns per atom (b/atom).
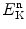 a set of partial microscopic cross sections σ i is usually available for the various possible interaction modes i. At a given
a set of partial microscopic cross sections σ i is usually available for the various possible interaction modes i. At a given 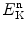 and target nucleus, the sum ∑ i σ i is referred to as the total microscopic cross section σ. Units of microscopic cross sections are cm2/atom, m2/atom, and barns per atom (b/atom).
and target nucleus, the sum ∑ i σ i is referred to as the total microscopic cross section σ. Units of microscopic cross sections are cm2/atom, m2/atom, and barns per atom (b/atom).(2)
Total macroscopic cross section Σ for a given attenuating medium is obtained by multiplying the total microscopic cross section σ (sum of all relevant partial microscopic cross sections) with the atomic density n □
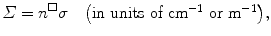
with the atomic density n □ defined as the number of atoms or nuclei N a per volume 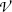 of the attenuator
of the attenuator
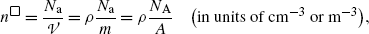
where N A is the Avogadro number (6.022×1023 mol−1), ρ is mass density of the attenuator, and A is the atomic weight or atomic mass number in g/mol.
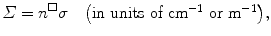
(9.3)
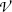 of the attenuator
of the attenuator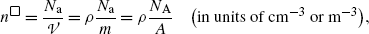
(9.4)
Like the microscopic cross section σ, the macroscopic cross section Σ depends on neutron kinetic energy 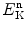 and physical properties of the attenuating medium. Relationship (9.4) is similar to the relationship in photon interactions with matter where the linear attenuation coefficient μ for a given photon interaction is a product of the atomic attenuation coefficient (also known as atomic cross section) a μ and the atomic density n □ or μ=n □ a μ.
and physical properties of the attenuating medium. Relationship (9.4) is similar to the relationship in photon interactions with matter where the linear attenuation coefficient μ for a given photon interaction is a product of the atomic attenuation coefficient (also known as atomic cross section) a μ and the atomic density n □ or μ=n □ a μ.
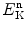 and physical properties of the attenuating medium. Relationship (9.4) is similar to the relationship in photon interactions with matter where the linear attenuation coefficient μ for a given photon interaction is a product of the atomic attenuation coefficient (also known as atomic cross section) a μ and the atomic density n □ or μ=n □ a μ.
and physical properties of the attenuating medium. Relationship (9.4) is similar to the relationship in photon interactions with matter where the linear attenuation coefficient μ for a given photon interaction is a product of the atomic attenuation coefficient (also known as atomic cross section) a μ and the atomic density n □ or μ=n □ a μ.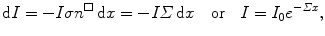
(9.5)
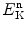 .
.(d) Macroscopic quantities: cross section Σ, mean free path Λ, and reaction rate 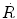 of neutrons traversing an attenuating medium depend upon atomic density n □ of the attenuating medium and kinetic energy
of neutrons traversing an attenuating medium depend upon atomic density n □ of the attenuating medium and kinetic energy 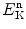 of the incident neutron.
of the incident neutron.
(e) Attenuation of a collimated neutron beam in an attenuator is expressed as
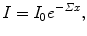
where I 0 and I are the incident fluence rate (2×1012 cm−2⋅s−1) and transmitted fluence rate (1.43×1012 cm−2⋅s−1), respectively, and Σ is the macroscopic cross section. Based on (9.8) and data provided on lead we now calculate:
 of neutrons traversing an attenuating medium depend upon atomic density n □ of the attenuating medium and kinetic energy
of neutrons traversing an attenuating medium depend upon atomic density n □ of the attenuating medium and kinetic energy 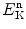 of the incident neutron.
of the incident neutron.(1)
Similarly to mean free path of photons, the mean free path Λ of neutrons is defined as that thickness Λ of attenuator that attenuates the neutron intensity I from original intensity I 0 to I 0/e or, expressed mathematically, we can say
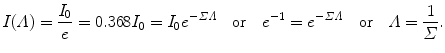
Mean free path Λ also is a measure of the mean distance that a neutron of given kinetic energy travels through a given attenuating medium before interacting with a nucleus. This definition is similar to the definition of mean free path 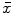 of photons in attenuating medium, where
of photons in attenuating medium, where 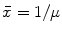 with μ the linear attenuation coefficient.
with μ the linear attenuation coefficient.
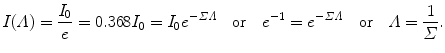
(9.6)
 of photons in attenuating medium, where
of photons in attenuating medium, where 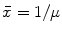 with μ the linear attenuation coefficient.
with μ the linear attenuation coefficient.(2)
Reaction rate 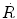 between neutrons and nuclei of attenuator is defined as the product of the macroscopic cross section Σ and neutron fluence rate
between neutrons and nuclei of attenuator is defined as the product of the macroscopic cross section Σ and neutron fluence rate 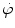 or
or
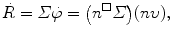
indicating that the reaction rate 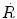 is linearly proportional to the atomic density n □, microscopic cross section σ, neutron density n, and velocity of neutrons υ. From (9.7) we note that the unit of reaction rate
is linearly proportional to the atomic density n □, microscopic cross section σ, neutron density n, and velocity of neutrons υ. From (9.7) we note that the unit of reaction rate 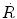 is cm−3⋅s−1.
is cm−3⋅s−1.
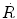 between neutrons and nuclei of attenuator is defined as the product of the macroscopic cross section Σ and neutron fluence rate
between neutrons and nuclei of attenuator is defined as the product of the macroscopic cross section Σ and neutron fluence rate 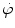 or
or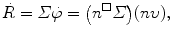
(9.7)
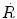 is linearly proportional to the atomic density n □, microscopic cross section σ, neutron density n, and velocity of neutrons υ. From (9.7) we note that the unit of reaction rate
is linearly proportional to the atomic density n □, microscopic cross section σ, neutron density n, and velocity of neutrons υ. From (9.7) we note that the unit of reaction rate 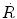 is cm−3⋅s−1.
is cm−3⋅s−1.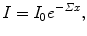
(9.8)
(1)
Total macroscopic cross section Σ.
(2)
Total microscopic cross section σ.
(3)
Mean free path Λ.
(4)
Neutron reaction rate 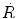 at a depth of 1 cm in lead attenuator.
at a depth of 1 cm in lead attenuator.
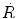 at a depth of 1 cm in lead attenuator.
at a depth of 1 cm in lead attenuator.(3)
Mean free path Λ is calculated using (9.6) as follows
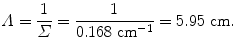
This means that a 10 MeV neutron travels on average about 6 cm in lead before it experiences one of the possible nuclear interactions with a lead nucleus of the attenuator.
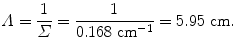
(9.11)
(4)
Reaction rate 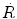 of a neutron beam is, according to (9.7), expressed as
of a neutron beam is, according to (9.7), expressed as 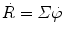 , where Σ is the total macroscopic cross section determined in (9.9) as Σ=0.168 cm−1 and
, where Σ is the total macroscopic cross section determined in (9.9) as Σ=0.168 cm−1 and 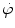 is the fluence rate at depth of x=1 cm in lead determined from (9.5) as follows
is the fluence rate at depth of x=1 cm in lead determined from (9.5) as follows
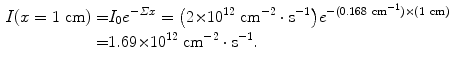
Reaction rate 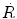 at a depth of x=1 cm in lead is now calculated as
at a depth of x=1 cm in lead is now calculated as
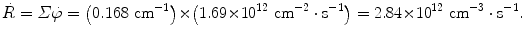
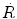 of a neutron beam is, according to (9.7), expressed as
of a neutron beam is, according to (9.7), expressed as 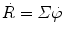 , where Σ is the total macroscopic cross section determined in (9.9) as Σ=0.168 cm−1 and
, where Σ is the total macroscopic cross section determined in (9.9) as Σ=0.168 cm−1 and 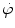 is the fluence rate at depth of x=1 cm in lead determined from (9.5) as follows
is the fluence rate at depth of x=1 cm in lead determined from (9.5) as follows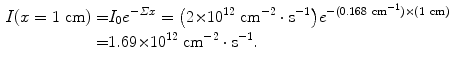
(9.12)
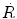 at a depth of x=1 cm in lead is now calculated as
at a depth of x=1 cm in lead is now calculated as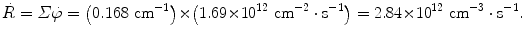
(9.13)
9.2 Neutron Interactions with Nuclei of the Absorber
9.2.Q1 (200)
Neutrons by virtue of being neutral particles can approach a target nucleus without any interference from a Coulomb repulsive or attractive force, since they, unlike protons and electrons, are not affected by nuclear charge. Once in close proximity to the target nucleus, neutrons can interact with it through the short-range attractive nuclear forces and trigger various nuclear reactions.
(a)
List and briefly describe at least 5 principal processes by which neutrons interact with nuclei of an absorber.
(b)
Provide a list and a brief description of the best-known neutron sources of use in medicine and of importance in medical physics.
SOLUTION:
(a) Six principal processes by which neutrons interact with nuclei of the absorber are:
A brief description of each of these neutron interactions is as follows:
(1)
Elastic scattering.
(2)
Inelastic scattering.
(3)
Non-elastic scattering.
(4)
Neutron capture.
(5)
Spallation.
(6)
Fission.
(1) Elastic scattering of neutron on absorber nucleus is the most important process for slowing down neutrons. The neutron collides with a nucleus of mass M that recoils with an angle ϕ with respect to the neutron initial direction of motion and the neutron is scattered by a scattering angle θ. Total energy and momentum are conserved in the elastic scattering interaction which means that kinetic energy lost by the neutron is equal to recoil energy of the target nucleus. The lighter is the target nucleus, the larger is the energy transfer from the neutron to the nucleus in an elastic scattering process; however, the target nucleus remains in the ground state.
(2) Inelastic scattering of neutron with absorber nucleus is similar to elastic scattering except that some of neutron’s kinetic energy is transferred to the nucleus not only to manifest itself as nuclear recoil kinetic energy but also to raise the nucleus from the ground state to an excited state. The nucleus de-excites by emitting high-energy γ rays and the neutron is scattered and moves on with kinetic energy that is lower than its incident energy. For inelastic scattering to occur, kinetic energy of the incident neutron must exceed the excitation energy of the nucleus. In contrast to elastic scattering, inelastic scattering is a threshold process and, when it occurs, neutron loses more energy in inelastic than in an elastic collision with absorber nucleus in order to account for the energy of the emitted γ ray. Therefore, only fast neutrons undergo inelastic scattering.
(3) Non-elastic scattering is in certain respect similar to inelastic scattering except that the secondary particle that is emitted is not a neutron. On the other hand, non-elastic scattering can also be considered neutron capture, except that the term neutron capture usually applies to capture of thermal neutron while non-elastic scatter typically deals with fast neutrons. An example of non-elastic scattering is
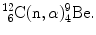
(4) Neutron capture is a term used to describe a nuclear reaction in which a thermal neutron collides with a target nucleus leading to neutron absorption in the target nucleus, formation of a new nuclide of different atomic mass number and/or atomic number from those of the target nucleus, and emission of a proton [(n,p) reaction: neutron capture with particle emission] or gamma ray [(n,γ) reaction: neutron capture with emission of γ radiation] in the process. Neutron capture, even after an immediate emission of a particle or γ ray, often results in an unstable radionuclide which decays with its own half-life that can range from a fraction of a second to many years depending on the nature of the neutron capture product. The majority of artificial radionuclides produced during the past decades have been discovered by means of thermal neutron capture in stable samples placed into nuclear fission reactors. When neutron capture is used for production of radionuclides or for analysis of trace elements in material samples, it is usually referred to as neutron activation instead of neutron capture.
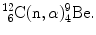
(9.14)
(5) Spallation is defined as fragmentation of a target into many smaller components as a result of impact or stress. Consequently, nuclear spallation is defined as disintegration of a target nucleus into many small residual components such as α particles and nucleons (protons and neutrons) upon bombardment with a suitable projectile such as light or heavy ion beams or neutrons. Nuclear spallation can also occur naturally in earth’s atmosphere as a result of exposure of nuclides to energetic cosmic rays such as protons.
An example of spallation is as follows
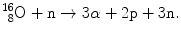
Most of the energy released in the spallation process is carried away by the heavier fragments that deposit their energy in the absorber locally. On the other hand, neutrons and de-excitation γ rays produced in spallation carry their energy to a remote location. Spallation can be used for production of radionuclides and for generation of intense neutron beams in spallation neutron generators.
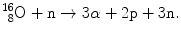
(9.15)
(6) Fission is a particular type of neutron interaction produced by bombardment of certain very high atomic number nuclei (Z≥92) by thermal or fast neutrons. The target nucleus fragments into two daughter nuclei of lighter mass and the fission process is accompanied with production of several fast neutrons. Nuclei that are capable of undergoing fission are called fissionable nuclei in general; nuclei that undergo fission with thermal neutrons are called fissile nuclei. Fission fragments combined with the nuclei that are subsequently formed through radioactive decay of fission fragments are called fission products.
(b) Neutron source is defined as a device that emits mono-energetic neutrons or a spectrum of neutrons. A wide variety of neutron sources are available ranging from small, encapsulated sources through particle accelerators and neutron generators to nuclear fission reactors.
(1) Nuclear fission reactor is the most abundant source of neutrons producing neutrons with an energy spectrum in the range from a few keV to over 10 MeV and average neutron energy of 2 MeV. Neutrons produced in research nuclear reactors are used for neutron scattering experiments, non-destructive testing, production of radionuclides for use in science, industry and medicine, and on a limited scale have been and still are also used in boron neutron capture therapy.
(2) Particle accelerators generate neutron beams by means of nuclear reactions with accelerated projectiles (protons or deuterons) striking a suitable target (typically of low atomic number) resulting in a product nucleus and a mono-energetic neutron beam. Best-known nuclear reactions for neutron production with neutron generators are exothermic reactions 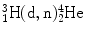 with a Q value of 17.6 MeV and
with a Q value of 17.6 MeV and 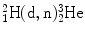 with a Q value of 3.3 MeV. Cyclotron-produced fast neutrons rely on acceleration of protons to about 50 MeV and directing them onto a beryllium target in which fast neutrons are produced for use in radiotherapy. Most intense pulsed neutron beams for industrial research are produced by spallation neutron sources that are accelerator based.
with a Q value of 3.3 MeV. Cyclotron-produced fast neutrons rely on acceleration of protons to about 50 MeV and directing them onto a beryllium target in which fast neutrons are produced for use in radiotherapy. Most intense pulsed neutron beams for industrial research are produced by spallation neutron sources that are accelerator based.
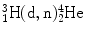 with a Q value of 17.6 MeV and
with a Q value of 17.6 MeV and 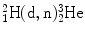 with a Q value of 3.3 MeV. Cyclotron-produced fast neutrons rely on acceleration of protons to about 50 MeV and directing them onto a beryllium target in which fast neutrons are produced for use in radiotherapy. Most intense pulsed neutron beams for industrial research are produced by spallation neutron sources that are accelerator based.
with a Q value of 3.3 MeV. Cyclotron-produced fast neutrons rely on acceleration of protons to about 50 MeV and directing them onto a beryllium target in which fast neutrons are produced for use in radiotherapy. Most intense pulsed neutron beams for industrial research are produced by spallation neutron sources that are accelerator based.(3) Radioactive neutron sources are produced by means of mixing an α emitter (such as radium-226 or americium-241) with a light metal (such as beryllium or boron) in powder form and encapsulating the mixture to make a neutron source generating neutrons through (α,n) reactions. The source intensity is governed by the half-life of the α emitter and the energy spectrum of emitted neutrons is continuous with maximum energy equal to the sum of the reaction Q value and kinetic energy of the α particle striking the nucleus.
(4) Photoneutron sources make use of photonuclear (γ,n) reactions and use mixtures of a mono-energetic γ emitter with beryllium metal. Photonuclear sources with mono-energetic γ emitters produce mono-energetic neutrons in contrast to (α,n) neutron sources that produce a spectrum of neutrons because of the random energy degradation of the α particles before they interact with the nucleus. The intensity of the photonuclear sources is governed by the half-life of the γ emitter component of the neutron source.
(5) Spontaneous fission neutron sources contain encapsulated high atomic number elements that undergo spontaneous fission and emit neutrons in the process. The best-known example of an intense spontaneous neutron fission source is californium-252 that was found useful in a wide range of specialized areas of science, industry, and medicine, such as the study of fission, neutron activation analysis, neutron radiography, well logging, nuclear reactor start up, and brachytherapy.
9.2.Q2 (201)
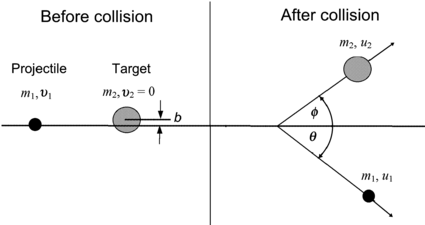
Elastic scattering of neutrons interacting with atomic nuclei of absorber is the most probable interaction of neutrons with absorbing medium for neutrons with kinetic energy E K≤2 MeV. The other possible interactions are inelastic scattering, neutron capture, spallation, and fission. In the energy range below 10 MeV the elastic scattering of neutrons can be treated classically, as shown schematically in Fig. 9.2 for two-particle elastic collision between projectile m 1 (neutron) moving with velocity υ 1 and a stationary target m 2 (nucleus of absorber), with θ the scattering angle of the projectile, ϕ the recoil angle of the target, and b the so-called impact parameter. After collision projectile m 1 continues with velocity u 1 and the target recoils with velocity u 2.
(a)
Use the classical principles of energy and momentum conservation to derive an expression for energy transfer ΔE K from the projectile m 1 to the stationary target m 2 in laboratory coordinate system.
(b)
Using the general expression for ΔE K derived in (a), express ΔE K for the specific example of neutron elastic scattering on a nucleus of the absorbing medium. Also state the energy transfer fraction f tr, maximum energy transfer fraction (f tr)max, and mean energy transfer fraction 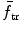 for elastic scattering of neutrons on target nuclei of atomic mass A.
for elastic scattering of neutrons on target nuclei of atomic mass A.
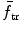 for elastic scattering of neutrons on target nuclei of atomic mass A.
for elastic scattering of neutrons on target nuclei of atomic mass A.(c)
Using the expression derived in (b) for kinetic energy transfer ΔE K from neutron to target nucleus in elastic scattering, determine mean energy 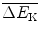 transferred from neutron to target nucleus in elastic scattering.
transferred from neutron to target nucleus in elastic scattering.
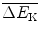 transferred from neutron to target nucleus in elastic scattering.
transferred from neutron to target nucleus in elastic scattering.(d)
Determine an expression for mean energy 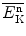 that a neutron carries from an elastic scattering event with target nucleus of atomic weight A. Calculate post-elastic scattering neutron kinetic energy as a fraction of incident neutron energy
that a neutron carries from an elastic scattering event with target nucleus of atomic weight A. Calculate post-elastic scattering neutron kinetic energy as a fraction of incident neutron energy 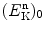 for the following target nuclei: hydrogen (A=1), cadmium (A=112), and uranium (A=238).
for the following target nuclei: hydrogen (A=1), cadmium (A=112), and uranium (A=238).
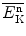 that a neutron carries from an elastic scattering event with target nucleus of atomic weight A. Calculate post-elastic scattering neutron kinetic energy as a fraction of incident neutron energy
that a neutron carries from an elastic scattering event with target nucleus of atomic weight A. Calculate post-elastic scattering neutron kinetic energy as a fraction of incident neutron energy 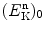 for the following target nuclei: hydrogen (A=1), cadmium (A=112), and uranium (A=238).
for the following target nuclei: hydrogen (A=1), cadmium (A=112), and uranium (A=238).
Fig. 9.2
Schematic diagram of an elastic collision between a projectile with mass m 1 and velocity υ 1 striking a stationary target m 2. Projectile is scattered with a scattering angle θ, target recoils with recoil angle ϕ, and the impact parameter is b. After the collision the velocity of the projectile is u 1 and the velocity of the recoiling target is u 2
SOLUTION:
(a) The kinetic energy transfer ΔE K from projectile m 1 to the target m 2 is determined classically in laboratory coordinate system using the conservation of energy and momentum laws as follows (see Fig. 9.2):
Equations (9.17) and (9.18) can, respectively, be written as follows
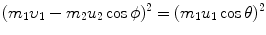
and
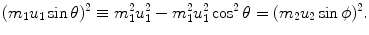
Inserting (9.19) into (9.20) gives the following expression
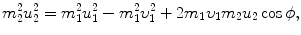
which, after inserting (9.16) multiplied by 2m 1, reads
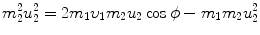
or
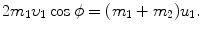
Since 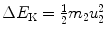 [i.e., energy transfer ΔE K from the projectile (incident particle) m 1 with kinetic energy (E K)0 to the target of mass m 2 is equal to recoil energy of the target
[i.e., energy transfer ΔE K from the projectile (incident particle) m 1 with kinetic energy (E K)0 to the target of mass m 2 is equal to recoil energy of the target 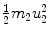 ], we get the following general expression for energy transfer ΔE K
], we get the following general expression for energy transfer ΔE K
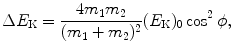
showing that the energy ΔE K transferred from the projectile to the recoiling target is governed by the recoil angle ϕ. With regard to recoil angle ϕ there are two special angles to consider:
(b) For the specific case of neutron scattering on an absorber nucleus we simplify the general classical expression (9.24) making the following changes:
(1)
Conservation of kinetic energy:
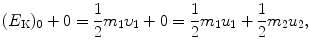
where (E K)0 is the kinetic energy of the projectile (incident particle) m 1.
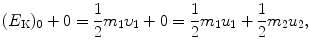
(9.16)
(2)
Conservation of momentum along abscissa (x) axis (note: the incident particle is moving along the abscissa axis in the positive direction):
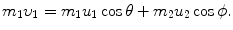
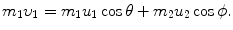
(9.17)
(3)
Conservation of momentum along ordinate (y) axis:
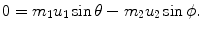
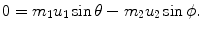
(9.18)
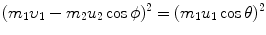
(9.19)
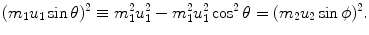
(9.20)
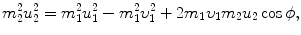
(9.21)
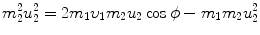
(9.22)
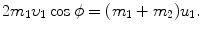
(9.23)
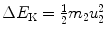 [i.e., energy transfer ΔE K from the projectile (incident particle) m 1 with kinetic energy (E K)0 to the target of mass m 2 is equal to recoil energy of the target
[i.e., energy transfer ΔE K from the projectile (incident particle) m 1 with kinetic energy (E K)0 to the target of mass m 2 is equal to recoil energy of the target 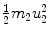 ], we get the following general expression for energy transfer ΔE K
], we get the following general expression for energy transfer ΔE K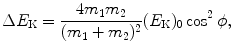
(9.24)
(1)
In an elastic, head-on collision, the recoil angle ϕ of the target is zero and ΔE K attains its maximum value (ΔE K)max for given projectile mass m 1, target mass m 2, and kinetic energy (E K)0 of the projectile expressed as a consequence of cos0∘=1 as
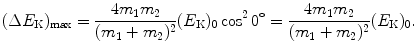
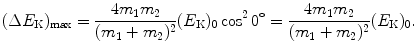
(9.25)
(2)
In grazing angle interaction between projectile and target, the recoil angle ϕ of the target is 90°, resulting in no energy transfer (ΔE K=0), as a consequence of cos90∘=0.
(3)
All other recoil angles are between 0° and 90° and the energy transfer from incident particle (neutron) to recoiling target (nucleus) is between (ΔE K)max and 0.
(1)
Projectile m 1 is the incident neutron with mass m n and incident kinetic energy 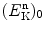 .
.
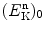 .
.(2)
Target is the nucleus of the attenuating medium with mass consisting of A nucleons (atomic mass number), i.e., m 2≈Am n where we assume that proton mass m p and neutron mass m n are approximately equal (m p=938.3 MeV/c 2≈m n=939.6 MeV/c 2).
With A the atomic weight of the target nucleus we now get the following simple expression for (9.24)
![$$ \Delta E_{\mathrm{K}} = \frac{4m_{\mathrm{n}}[Zm_{\mathrm{p}}+(A-Z)m_{\mathrm{n}}]}{\{m_{\mathrm{n}} + [Zm_{\mathrm{p}}+(A-Z)m_{\mathrm{n}}]\}^{2}} \bigl(E_{\mathrm{K}}^{\mathrm{n}} \bigr)_{0}\cos^2 \phi \approx \frac{4A}{(1+A)^2} \bigl(E_{\mathrm{K}}^{\mathrm{n}}\bigr)_{0}\cos^2 \phi, $$](/wp-content/uploads/2016/04/A212719_1_En_9_Chapter_Equ26.gif)
or we can state that the energy transfer fraction 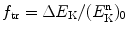 that is, the fraction of kinetic energy of the incident neutron transferred to the stationary target, is
that is, the fraction of kinetic energy of the incident neutron transferred to the stationary target, is
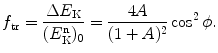
![$$ \Delta E_{\mathrm{K}} = \frac{4m_{\mathrm{n}}[Zm_{\mathrm{p}}+(A-Z)m_{\mathrm{n}}]}{\{m_{\mathrm{n}} + [Zm_{\mathrm{p}}+(A-Z)m_{\mathrm{n}}]\}^{2}} \bigl(E_{\mathrm{K}}^{\mathrm{n}} \bigr)_{0}\cos^2 \phi \approx \frac{4A}{(1+A)^2} \bigl(E_{\mathrm{K}}^{\mathrm{n}}\bigr)_{0}\cos^2 \phi, $$](/wp-content/uploads/2016/04/A212719_1_En_9_Chapter_Equ26.gif)
(9.26)
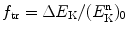 that is, the fraction of kinetic energy of the incident neutron transferred to the stationary target, is
that is, the fraction of kinetic energy of the incident neutron transferred to the stationary target, is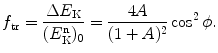
(9.27)
Like in the general case described by (9.24), we again have two special angles: ϕ=0 and ϕ=90∘. For direct, head-on collision where the nucleus recoils with ϕ=0 the energy transfer ΔE K and energy transfer fraction f tr attain its maximum possible value, respectively, since cos0∘=1 in (9.26) and (9.27)
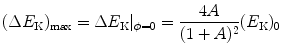
and
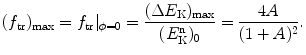
Note that for a direct hit (ϕ=0), the maximum energy transfer fraction (f tr)max that is transferred from the incident neutron to recoil nucleus has the following properties:
For grazing incidence where the nucleus recoils with ϕ=90∘ the energy transfer fraction f tr attains its minimum value of f tr=0, as a result of cos0∘=0 in (9.27)
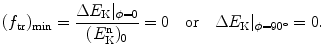
(c) Mean kinetic energy transfer 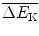 from neutron to target nucleus is calculated by averaging (9.26) over the recoil angle ϕ of the target nucleus as follows
from neutron to target nucleus is calculated by averaging (9.26) over the recoil angle ϕ of the target nucleus as follows
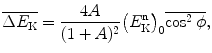
with 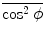 determined as
determined as
![$$ \overline{\cos^2\phi}= \frac{\int^{\pi/2}_{0}\cos^2\phi\,\mathrm{d}\phi}{\int^{\pi/2}_{0}\mathrm{d}\phi} = \frac{1}{\pi }\int^{\pi/2}_{0}\frac{1+\cos(2\phi)}{2}\, \mathrm{d}(2\phi)=\frac{1}{\pi} \biggl[\phi+\frac{\sin(2\phi)}{2} \biggr]^{\frac{\pi}{2}}_0=\frac{1}{2}. $$](/wp-content/uploads/2016/04/A212719_1_En_9_Chapter_Equ32.gif)
Mean energy transfer 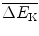 from neutron to target nucleus is thus given as follows
from neutron to target nucleus is thus given as follows
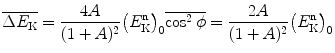
and similarly for the mean energy transfer fraction 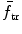
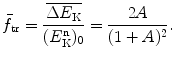
Equations (9.29) and (9.32) show that to moderate neutrons (that is to slow them down) with the fewest number of elastic collisions, target nuclei with as low as possible atomic weight A should be used as absorber medium. Thus, the most efficient nucleus for this purpose is hydrogen with A=1 for which (ΔE K)max=(E K)0, 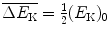 , and
, and 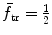 as seen by inserting A=1 into (9.28), (9.29), and (9.32), respectively.
as seen by inserting A=1 into (9.28), (9.29), and (9.32), respectively.
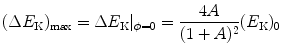
(9.28)
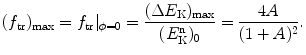
(9.29)
(1)
Depends only on the atomic mass number A (atomic weight) of the target nucleus.
(2)
Is equal to 1 when the target nucleus is the hydrogen nucleus (proton) with (A=1).
(3)
Decreases from (f tr)max=1 as the target mass increases from A=1.
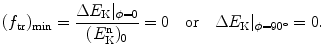
(9.30)
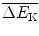 from neutron to target nucleus is calculated by averaging (9.26) over the recoil angle ϕ of the target nucleus as follows
from neutron to target nucleus is calculated by averaging (9.26) over the recoil angle ϕ of the target nucleus as follows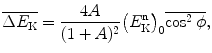
(9.31)
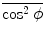 determined as
determined as![$$ \overline{\cos^2\phi}= \frac{\int^{\pi/2}_{0}\cos^2\phi\,\mathrm{d}\phi}{\int^{\pi/2}_{0}\mathrm{d}\phi} = \frac{1}{\pi }\int^{\pi/2}_{0}\frac{1+\cos(2\phi)}{2}\, \mathrm{d}(2\phi)=\frac{1}{\pi} \biggl[\phi+\frac{\sin(2\phi)}{2} \biggr]^{\frac{\pi}{2}}_0=\frac{1}{2}. $$](/wp-content/uploads/2016/04/A212719_1_En_9_Chapter_Equ32.gif)
(9.32)
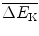 from neutron to target nucleus is thus given as follows
from neutron to target nucleus is thus given as follows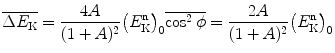
(9.33)
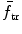
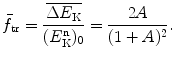
(9.34)
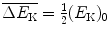 , and
, and 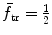 as seen by inserting A=1 into (9.28), (9.29), and (9.32), respectively.
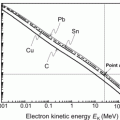
as seen by inserting A=1 into (9.28), (9.29), and (9.32), respectively.In Fig. 9.3 we plot, against atomic mass number A, the maximum energy transfer fraction (f tr)max given in (9.29) and the mean energy transfer fraction 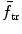 given in (9.32) and show that the two energy transfer fractions decline rapidly roughly as 1/A with increasing A from their high values of 1 and 0.5, respectively, for hydrogen and amount to only 0.017 and 0.0085, respectively, for uranium-238, as also indicated in Fig. 9.3. Several other nuclides are also identified in the graph.
given in (9.32) and show that the two energy transfer fractions decline rapidly roughly as 1/A with increasing A from their high values of 1 and 0.5, respectively, for hydrogen and amount to only 0.017 and 0.0085, respectively, for uranium-238, as also indicated in Fig. 9.3. Several other nuclides are also identified in the graph.
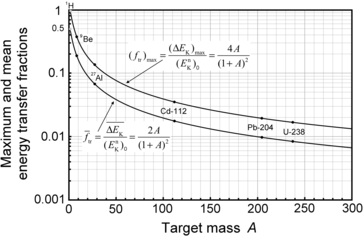
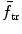 given in (9.32) and show that the two energy transfer fractions decline rapidly roughly as 1/A with increasing A from their high values of 1 and 0.5, respectively, for hydrogen and amount to only 0.017 and 0.0085, respectively, for uranium-238, as also indicated in Fig. 9.3. Several other nuclides are also identified in the graph.
given in (9.32) and show that the two energy transfer fractions decline rapidly roughly as 1/A with increasing A from their high values of 1 and 0.5, respectively, for hydrogen and amount to only 0.017 and 0.0085, respectively, for uranium-238, as also indicated in Fig. 9.3. Several other nuclides are also identified in the graph.
Fig. 9.3
Maximum and mean energy transfer fractions (f tr)max and 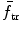 for elastic collision of neutrons with moderator nuclei of atomic weight A
for elastic collision of neutrons with moderator nuclei of atomic weight A
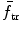 for elastic collision of neutrons with moderator nuclei of atomic weight A
for elastic collision of neutrons with moderator nuclei of atomic weight A (d) Mean kinetic energy 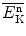 of post-elastic collision neutron is calculated as mean energy transfer
of post-elastic collision neutron is calculated as mean energy transfer 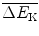 from neutron to target nucleus subtracted from incident neutron energy
from neutron to target nucleus subtracted from incident neutron energy 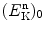
![$$ \overline{E^{\mathrm{n}}_{\mathrm{K}}}=\bigl(E^{\mathrm{n}}_{\mathrm{K}} \bigr)_0 - \overline{\Delta E_{\mathrm{K}}} = \bigl(E^{\mathrm{n}}_{\mathrm{K}} \bigr)_0 \biggl[1-\frac{2A}{(1+A)^2}\biggr]=\bigl(E^{\mathrm{n}}_{\mathrm{K}} \bigr)_0\frac{1+A^2}{(1+A)^2}. $$](/wp-content/uploads/2016/04/A212719_1_En_9_Chapter_Equ35.gif)
Fractions of incident energy 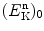 that a neutron retains after elastic collision with a given target nucleus are calculated from (9.35) as follows:
that a neutron retains after elastic collision with a given target nucleus are calculated from (9.35) as follows: 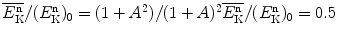 for H (A=1); 0.858 for C (A=12); 0.982 for Cd (A=112); and 0.992 for U (A=238).
for H (A=1); 0.858 for C (A=12); 0.982 for Cd (A=112); and 0.992 for U (A=238).
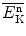 of post-elastic collision neutron is calculated as mean energy transfer
of post-elastic collision neutron is calculated as mean energy transfer 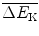 from neutron to target nucleus subtracted from incident neutron energy
from neutron to target nucleus subtracted from incident neutron energy 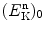
![$$ \overline{E^{\mathrm{n}}_{\mathrm{K}}}=\bigl(E^{\mathrm{n}}_{\mathrm{K}} \bigr)_0 - \overline{\Delta E_{\mathrm{K}}} = \bigl(E^{\mathrm{n}}_{\mathrm{K}} \bigr)_0 \biggl[1-\frac{2A}{(1+A)^2}\biggr]=\bigl(E^{\mathrm{n}}_{\mathrm{K}} \bigr)_0\frac{1+A^2}{(1+A)^2}. $$](/wp-content/uploads/2016/04/A212719_1_En_9_Chapter_Equ35.gif)
(9.35)
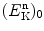 that a neutron retains after elastic collision with a given target nucleus are calculated from (9.35) as follows:
that a neutron retains after elastic collision with a given target nucleus are calculated from (9.35) as follows: 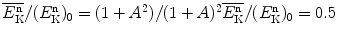 for H (A=1); 0.858 for C (A=12); 0.982 for Cd (A=112); and 0.992 for U (A=238).
for H (A=1); 0.858 for C (A=12); 0.982 for Cd (A=112); and 0.992 for U (A=238).9.2.Q3 (202)
Moderation (slowing down) of neutrons in nuclear reactors is very important for sustaining fission reaction. Neutrons generated in a typical fission reaction have kinetic energy 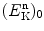 of about 2 MeV, while thermal neutrons of kinetic energy
of about 2 MeV, while thermal neutrons of kinetic energy 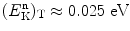 are required for efficient fission of uranium-235 (highest fission capture cross section) and for sustaining a fission chain reaction. A moderator is used for reduction of kinetic energy (thermalization) of neutrons generated in fission reactions and this is achieved through multiple, mainly elastic, scattering of neutrons whereby some of the neutron kinetic energy is transferred to the moderator in each scattering event. The mean energy
are required for efficient fission of uranium-235 (highest fission capture cross section) and for sustaining a fission chain reaction. A moderator is used for reduction of kinetic energy (thermalization) of neutrons generated in fission reactions and this is achieved through multiple, mainly elastic, scattering of neutrons whereby some of the neutron kinetic energy is transferred to the moderator in each scattering event. The mean energy 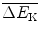 transferred from neutron to target nucleus of the moderator in each scattering interaction depends on incident neutron energy
transferred from neutron to target nucleus of the moderator in each scattering interaction depends on incident neutron energy 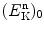 as well as on the atomic mass number A of the target nucleus and is given by
as well as on the atomic mass number A of the target nucleus and is given by
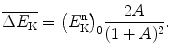
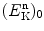 of about 2 MeV, while thermal neutrons of kinetic energy
of about 2 MeV, while thermal neutrons of kinetic energy 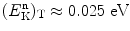 are required for efficient fission of uranium-235 (highest fission capture cross section) and for sustaining a fission chain reaction. A moderator is used for reduction of kinetic energy (thermalization) of neutrons generated in fission reactions and this is achieved through multiple, mainly elastic, scattering of neutrons whereby some of the neutron kinetic energy is transferred to the moderator in each scattering event. The mean energy
are required for efficient fission of uranium-235 (highest fission capture cross section) and for sustaining a fission chain reaction. A moderator is used for reduction of kinetic energy (thermalization) of neutrons generated in fission reactions and this is achieved through multiple, mainly elastic, scattering of neutrons whereby some of the neutron kinetic energy is transferred to the moderator in each scattering event. The mean energy 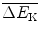 transferred from neutron to target nucleus of the moderator in each scattering interaction depends on incident neutron energy
transferred from neutron to target nucleus of the moderator in each scattering interaction depends on incident neutron energy 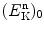 as well as on the atomic mass number A of the target nucleus and is given by
as well as on the atomic mass number A of the target nucleus and is given by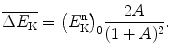
(9.36)
(a)
Derive a recurrence equation to describe neutron kinetic energy 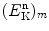 after an incident neutron with initial kinetic energy
after an incident neutron with initial kinetic energy 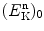 undergoes a sequence of m elastic scattering collisions with nuclei of atomic mass number A.
undergoes a sequence of m elastic scattering collisions with nuclei of atomic mass number A.
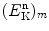 after an incident neutron with initial kinetic energy
after an incident neutron with initial kinetic energy 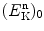 undergoes a sequence of m elastic scattering collisions with nuclei of atomic mass number A.
undergoes a sequence of m elastic scattering collisions with nuclei of atomic mass number A.(b)
Use the recurrence equation derived in (a) to determine the required number of elastic scattering interactions to moderate neutrons with 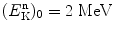 down to thermal energy
down to thermal energy 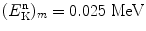 in hydrogen, carbon, cadmium, lead, and uranium.
in hydrogen, carbon, cadmium, lead, and uranium.
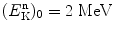 down to thermal energy
down to thermal energy 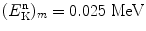 in hydrogen, carbon, cadmium, lead, and uranium.
in hydrogen, carbon, cadmium, lead, and uranium.SOLUTION:
(a) The simplest manner in which one can derive a recurrence equation to recursively define a sequence of events is to write the first few terms of the sequence and from a comparison of the terms deduce the recurrence equation. Moderation (slowing down) of neutrons by elastic scattering is a good example of a sequence that can be described by a recurrence equation and we derive the general equation by laying out the first few terms of the neutron slowing down process through elastic scattering.
For each elastic scattering event the mean energy 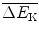 transferred from the incident neutron of kinetic energy
transferred from the incident neutron of kinetic energy 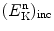 to the moderator is derived in (9.35) and given in (9.36). Consequently, we can write the kinetic energy of the neutron after each elastic scattering event as the difference between
to the moderator is derived in (9.35) and given in (9.36). Consequently, we can write the kinetic energy of the neutron after each elastic scattering event as the difference between 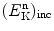 and
and 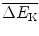 as follows
as follows
![$$ \bigl(E^{\mathrm{n}}_{\mathrm{K}}\bigr)_{\mathrm{after}} = \bigl(E^{\mathrm{n}}_{\mathrm{K}}\bigr)_{\mathrm{inc}} - \overline {\Delta E_{\mathrm{K}}} = \bigl(E^{\mathrm{n}}_{\mathrm{K}}\bigr)_{\mathrm{inc}} \biggl[1-\frac{2A}{(1+A)^2}\biggr]=\bigl(E^{\mathrm{n}}_{\mathrm{K}} \bigr)_{\mathrm{inc}} \biggl[\frac{1+A^2}{(1+A)^2}\biggr]. $$](/wp-content/uploads/2016/04/A212719_1_En_9_Chapter_Equ37.gif)
The first few elastic scattering events in the slowing down of a neutron in a sequence of elastic scattering events are now expressed as follows:
Get Clinical Tree app for offline access
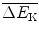 transferred from the incident neutron of kinetic energy
transferred from the incident neutron of kinetic energy 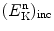 to the moderator is derived in (9.35) and given in (9.36). Consequently, we can write the kinetic energy of the neutron after each elastic scattering event as the difference between
to the moderator is derived in (9.35) and given in (9.36). Consequently, we can write the kinetic energy of the neutron after each elastic scattering event as the difference between 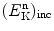 and
and 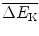 as follows
as follows![$$ \bigl(E^{\mathrm{n}}_{\mathrm{K}}\bigr)_{\mathrm{after}} = \bigl(E^{\mathrm{n}}_{\mathrm{K}}\bigr)_{\mathrm{inc}} - \overline {\Delta E_{\mathrm{K}}} = \bigl(E^{\mathrm{n}}_{\mathrm{K}}\bigr)_{\mathrm{inc}} \biggl[1-\frac{2A}{(1+A)^2}\biggr]=\bigl(E^{\mathrm{n}}_{\mathrm{K}} \bigr)_{\mathrm{inc}} \biggl[\frac{1+A^2}{(1+A)^2}\biggr]. $$](/wp-content/uploads/2016/04/A212719_1_En_9_Chapter_Equ37.gif)
(9.37)
(1)
We start with an incident neutron with kinetic energy 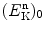 striking the moderator of atomic weight A. As suggested in (9.37), the kinetic energy
striking the moderator of atomic weight A. As suggested in (9.37), the kinetic energy 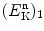 of the neutron after the first elastic scattering interaction is given as
of the neutron after the first elastic scattering interaction is given as
![$$ \bigl(E^{\mathrm{n}}_{\mathrm{K}}\bigr)_{1} = \bigl(E^{\mathrm{n}}_{\mathrm{K}}\bigr)_{0} \biggl[ \frac{1+A^2}{(1+A)^2}\biggr]. $$](/wp-content/uploads/2016/04/A212719_1_En_9_Chapter_Equ38.gif)
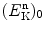 striking the moderator of atomic weight A. As suggested in (9.37), the kinetic energy
striking the moderator of atomic weight A. As suggested in (9.37), the kinetic energy 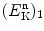 of the neutron after the first elastic scattering interaction is given as
of the neutron after the first elastic scattering interaction is given as![$$ \bigl(E^{\mathrm{n}}_{\mathrm{K}}\bigr)_{1} = \bigl(E^{\mathrm{n}}_{\mathrm{K}}\bigr)_{0} \biggl[ \frac{1+A^2}{(1+A)^2}\biggr]. $$](/wp-content/uploads/2016/04/A212719_1_En_9_Chapter_Equ38.gif)
(9.38)
(2)
Incident kinetic energy for the second scattering event is now 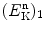 so that, according to (9.37) in conjunction with (9.38), we write the neutron kinetic energy
so that, according to (9.37) in conjunction with (9.38), we write the neutron kinetic energy 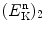




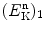 so that, according to (9.37) in conjunction with (9.38), we write the neutron kinetic energy
so that, according to (9.37) in conjunction with (9.38), we write the neutron kinetic energy 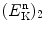
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree