A scientist predicts the secrets of the natural dynamic processes happening in our body through mathematical modeling. He or she then looks for its experimental verification in clinical situation through the use of the technological wonder, the MRI (magnetic resonance imaging), machine. This is done in vivo situation of an organ of the body as well as using the phantom laboratory experiments simulating a real life situation. A disagreement between what is observed and what is modeled is translated into a better physical and chemical model for further experimentation. This iterative process followed by a scientist leads to not only better understanding of the human body but also paves the way for the design of a better MRI machine. The nuclear magnetic resonance (NMR) phenomena was at the root of the curiosity research more than half a century ago. It has now resulted into the commercial MRI machine we have today. Over the last decade or so there is now demand on the technology to use multi-quantum dipole magnetic spin processes toward imaging rather than just the prevalent single-quantum spin processes. The multi-quantum processes happen in the molecular nm (nano meter) level and represent true natural character of events in progress in our body. The triple-quantum (coherent quantum spin action of three spins identical or of different species pointing in the same direction near and far) sodium imaging in vivo of the human brain is a typical example among the research and development efforts in progress in the direction of multi-quantum MRI (MQMRI).

NMR spectroscopy of elements in human body is now routinely used as a diagnostic tool. It is to make in depth analysis in particular in vivo in an ensemble of nuclear spins in a particular organ of the human body. The basics of the cooperative (multiple-species) electronic quantum structure of the elements in an ensemble like our body needs to be understood from the grass roots. This knowledge can then be used to derive the metabolic synaptic etc. activities of the chemical elements in our body in time and space.

Slowly NMR spectroscopy has found integration with the in vivo imaging in MRI. One should remember that the quantum spectroscopy of each element helped classify the chemical elements as arranged in, ‘The Periodic Table of The Elements’ (please see Appendix A1 for the place of the useful magnetic dipole and electrical quadrupole nuclei in the Periodic Table). It is interesting to mention that the Periodic Table of Elements was completely worked out more than century ago based on the quantum energy structure of each element. Behind this classification in detail is the arrangement of electrons in orbits around the nucleus and that of the protons and neutrons inside the nucleus. The, individual orbit-electron-atom arrangement in an element makes the unique place for each element in the ‘Periodic Table’ and controls its chemical and physical properties. The standard quantum electronic structure of each individual element worked out through spectroscopy can be accessed in a ‘Handbook of Chemistry And Physics’ and in routine text books of chemistry and physics available in a university science library throughout the world. But when the chemical elements are part of an ensemble e.g. macromolecules in our body the spectroscopy takes up a totally different horizon. The curiosity then asks the following questions. How do the chemical elements manipulate life? Why they are the architecture of the ensemble like our body is? Why and how do they acquire a typical macromolecular structure so important to our daily life?

The human civilization at large need to engage in research and development efforts to find out the answers to the above questions. MRI being a non invasive technology provides an appropriate tool for this purpose. It is important to note as follows. If the knowledge developed remains as the privileged property among the higher elite levels of the scientific community e.g. in the universities, research institutions, private companies etc. and is not passed on to the mass education e.g. the secondary school level the gap between the known and the unknown will eventually become insurmountable. If there are no minds to know more then we are left with obsolete machines doing routine jobs with limited future. Think of the coming generations. What are they going to do? There is wilderness of technology available to society in different fields e.g., tele-communication, imaging technology, etc. today. But how to use a technology appropriately, efficiently and rediscover and improve it on a continuous scientific basis seems of little concern to our leaders. This book has been written to pave the way to stimulate the reduction of the gap of illiteracy between science and technology. There is need starting from the production and use of technology to the education as to how to use efficiently and why and where to use it. There can be a healthy supply of common-minded decision making leaders only if three is an education about science of the masses at the secondary school level of education. This unfortunately in fact is on fast decline world wide. Sports, recreation, selfish bureaucratic financial manipulations, media, etc., have taken over the science of reason and the intuition in today’s life.

Life today is under too much complex stress created by bureaucratic constraints. There is no basic freedom to be just you. Now let us try to analyze what is the chemistry of the human body in the light of the magnetic materials present in the body. It is seen that among all the elements in a biological system like ours there are some potentially valuable magnetic isotopes. We have a small group of dipole magnetic nuclei, ¹H, ²H, ¹³c, ¹⁵N, ¹⁹F and ³¹P (the superscript shown in each element is the mass number of the element approximately equal to the total number of the protons and the neutrons in the nucleus as the mass equivalent number) present in our body. One may ask a question at this point why nature has chosen only some particular elements and not others as a source of life progression? One can find out a scientific reason for that. But at the moment we have no choice but to leave it just as a secret of the nature. The above listed elements intrinsically at the lowest level of quantum energy (the ground state) have an atomic moment (expressed in symbol as μ_L) and a nuclear magnetic (expressed in symbol as moment μ_N) moment. Both types of magnetic moments are identical in their behavior but they differ in the size of their magnitudes and the strength of the forces involved. The dipole magnetic moment is expressed in terms of the angular momentum which generates it. In the lowest state, the nuclear magnetic dipole moment is symbolically expressed in the two lowest (higher states are possible) possible quantum states as I = ±1/2. This is only a simplified qualitative quantum symbolic expression. In magnitude a fundamental physical constant will be multiplied to it to get an exact magnitude. In the case of a nucleus this constant is called as the nuclear magneton and in the atomic case the Bohr magneton. We know in the case of an tom that an electron is bound to the atom and performs an orbital motion around the nucleus. This is the origin of the atomic magnetic moment. In addition an electron also spins around its own axis. In a physical meaning of the quantum language the electron spin (the angular momentum around its own axis) has two simplest possible quantum values S = ±(1/2). The electrons angular momentum around the nucleus, L, is expressed through the quantum number l = ±1 in the lowest state. It can have higher quantum values, ±2, ±3,…etc. The reader is reminded that the above simplified quantum structure for the angular momentum is only obtained by application of a static magnetic field in a chosen direction called as the z- direction. This is the result of the planar atomic orbit quantization the magnetic field creates.

The idea is that when we rotate the spins from z-direction (by the application of RF pulses) into the x–y plane they can have higher possible quantum states of, ±2, ±3, …etc., by absorbing the applied RF radiation. In an ensemble like our brain the atoms combine to form molecules and the molecules combine to form macromolecules. The angular momentum (also loosely refereed to as spin) of the electrons, atoms, and molecules all add up to produce a resultant. If there were no quantum interactions among molecules the respective angular momenta just add up as scalar quantities. But more often than not the molecules do interact as that is the source of continuation of the life in our brain. Thus the molecular quantum coherence (interaction) imaging (MQMRI) needs to be the tool of technology of the future MRI. We are hopefully progressing in that direction now. The reader is reminded that in the MRI literature the symbolic mathematical equations about the magnetic dipole moment, angular momentum, quantum numbers etc. may look identical in their appearance. In true sense they may represent different magnitudes, different meanings, etc. The ratio of the dipole magnetic moment to the angular momentum is referred to as the gyromagnetic ratio (GMR). This is the link between the dipole magnetic moment and the angular momentum which generates it. Unfortunately we can not measure in the laboratory the angular momentum directly. The measurement of the magnetic moment in the MRI situation provides an indirect measurement of the angular momentum of atoms and nuclei in an imaging situation.

The vibrations of magnetic moments produced by the incident RF radiation becomes the source of the varied electrical signal across the brain. The Planck’s content ћ is multiplied with the frequency (resonance) of the radiation i.e. the radio frequency (RF) radiation to get the energy absorbed in the MRI processes. The RF radiation is in the 100 MHz (megahertz, i.e., ~10⁸ Hz) in the MRI perspective. RF radiation is used to excite an electron in its orbit. It provides the energy of the transition between two consecutive quantum states of the magnetic moment of the atom. In the MRI literature the mathematical expression, I = ±1/2 is normally retained (for the magnetic moment and the angular momentum) and multiplication by ћ is left out for simplicity. The angular Planck’s constant in magnitude is given as ћ = 1.055 × 10⁻³⁴ Js (joules second) = 0.6582 × 10⁻¹⁵ eVs (electron volt second). The conversion from Js unit to the eV unit is given by 1 eV = 1.602 × 10⁻¹⁹ J. The energy of electron transition to a next higher energy state is given as, E = ћf ~ 10⁻²⁷ Jor ~ 10⁻⁷ eV. This should give the reader a rough idea about the order of energies involved in MRI. We only have here μeV (micro electron volt) range of energies. The energies involved are very small and are of little danger to the body. Thus one can see the grounds of MRI as a non-invasive technology. One should remember that quantum energy structure of an electron in an orbit around the nucleus is not unique to electrons only. The protons and neutrons inside the nucleus have an analogous quantum energy structure. In a small volume of our body atomic and nuclear processes are in interaction with each other to produce an overall effect. One, should, compare the energies involved in MRI to the X-ray imaging. In X-ray imaging we have energy ~10⁶ eV i.e. the Mev (mega electron volt) range. This can be very dangerous to the human body in particular the brain.

One should note the intrinsic electron spin originates from the intrinsic circular motion of the single electron around its own axis. But an electron is also in an orbit around the nucleus. The electron spin (rotation) around the nucleus creates an orbital magnetic moment of μ_l = (g_l)(μ_b)(m_l)L, where g_l is called as the spectroscopic splitting (degeneracy) factor, μ_b (called as the Bohr Magneton) = [(eћ/(2m_e)] = 0.927 × 10⁻²³ amp-m² the fundamental (the smallest unit) magnetic moment, e = the electron charge = 1.602 × 10⁻¹⁹ C and m_l = orbital magnetic quantum number and L the orbital angular momentum.. The magnetic quantum number m_l has the possible quantum states (numbers) = 0, ±1, ±2, ±3, …, in a static magnetic field applied in the z-direction. In addition to the electron orbiting the nucleus the protons and the neutrons are also in circular motion inside the nucleus. They have identical quantum spin structure. One can say a small volume (called as voxel in MRI literature) in our brain is a typical ensemble of the electrons, nuclei, atoms, molecules. They are present within a complex inter and intra macromolecular structure of tissues, fluids, etc. This is a micro representation of the brain. In the brain when a voxel (a small volume) is subjected to an external static magnetic field (say in the z-direction) the spins (atomic and molecular magnets) in the fluids and in the stationary soft matter reorganize themselves into an ordered resultant quantized mixture of energy states. The spins now have the electrons, atoms and molecules with their magnetic axis aligned along the externally applied magnetic field. One should note without the static magnetic field applied the spins are randomly oriented and the total magnetism in a small volume (voxel), may be zero. But this ideal situation is possible only provided the volume is biologically isotropic in space an time.

In a real life situation in our brain the spins do not diffuse (translate, rotate, etc.) fast enough and far enough to neutralize each other. The anisotropic medium in-between deflects them from their course of action i.e. the tendency to neutralize each other. Consequently a small resultant magnetism is produced in a voxel. It is measured through a physical quantity called as the magnetic moment per unit volume or the susceptibility. Anisotropic diffusion of spins along different directions becomes the source of imaging referred to as the diffusion tensor imaging. There are many characteristic parameters for obtaining image in conventional MRI. The commonly in use are the anisotropic relaxation of longitudinal (T₁) and transverse (T₂) relaxation times of spins on irradiation of spins in a voxel with RF radiation. One should realize that the magnetic axis of the tiny atomic dipole-magnet is perpendicular to the orbital plane of the electrons around the nucleus. However these axes are randomly oriented in pace. The application of the static magnetic field along the z-direction simplifies the chaotic 3-dimensional random system into a simpler easier to handle planar quantum system in the X–Y pane. One may ask a question then how the nature lets the chaotic network of molecules make the brain think and manipulate action in such an orderly fashion. The answer to that question is not so straightforward. We know that the orbital motion of electrons in an atom in a free space from simple physics principles would lead to creation of an internal magnetic field on the electron of around 1 T.

In a condensed matter space like our brain with medium of various fluids the field will be somewhat less due to the dielectric properties of the medium where charge motion takes place. The electrons, atoms, molecules are part of macromolecules. The macromolecules farther form a cohesive group of the size of nms (nano meters) to microns size are part of mutual interactions. The effective internal magnetic field in space can be considered as large when a large group of molecules are involved. This field is what provides an odder locally to let the molecules perform their function in a coherent orderly manner. One need to explore the order in the brain on the nm scale with little disturbance to the inside order from outside. That technology yet does not exist. The MQ-MRI (multi-quantum magnetic resonance imaging) is a step in that direction. The present MRI technology only humbly tries to unscramble the naturally present order in the brain system. Inside there is a complicated electric–magnetic system that is operative in our brain. We externally manipulate the internal system through the applied static magnetic field of around 3 T and the RF radiation to make some sense. But this has to be done in such way as not to disturb or alter the internal brain order. We are in a dilemma. Aren’t we?

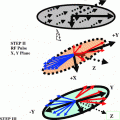
In MRI the RF radiation is applied along the three orthogonal directions (x, y, z) to the brain system. It excites the planar quantum (called as the quantization) system to higher magnetic quantum energy states. The higher energy states naturally come back to their original ground state in a microsecond. A series of RF pulses are used to excite a voxel. The quantized system (created by virtue of the applied static magnetic field) releases back the extra energy absorbed from the applied RF radiation. The out coming radiation carries with it the signatures of the physical and chemical events happening in space and time in the brain. The returned electrical signals are then converted into the shape of a picture which we call the MRI. The structure of the brain system depicted in the MRI picture can be translated to the real time bio-medical quantum mechanical events happening in the brain. For a detailed quantum mechanical treatment of an ensemble of atoms and molecules the reader should refer to a standard text in physics. The references [1–4] should prove helpful to the reader in this matter.

One should always remember that the spin (the magnetic dipole character) of an atom and of a nucleus arises due to the circulation of the electrical charges i.e. due to the electrons in an atom and the protons and neutrons in the nucleus respectively. The circular motion of electrons in atoms functionally is very much like the linear motion of the electrons when an electrical current flows through a copper wire when subjected to a potential difference between the two ends of the copper wire. In the linear motion it is the linear momentum which is important. In a circular copper coil geometry where the electric current is produced around the coil there is a magnetic field produced at the centre directed along the axis of the coil. The magnetic field reverses with the reversal of the direction of the electrical current. In the atomic and nuclear case we are encountering rotational motion and it is angular momentum that steals the show. In the atomic situation an electron could be circulating clockwise or anticlockwise and thus the degeneracy is ±1; the spin in turn is written as, numbers I = 1/2 or −1/2. As earlier pointed out in exact physical magnitude it should be written as ±1/2 ћ. Here ћ, the Planck’s fundament quantum (quantity) and is the source of the fundamental quantum of energy. The magnetic dipole elements present in our body are the basic source of imaging labels in the MRI. It is important to point out here that the electrical charges in our body play a very important role in the moment to moment happening the physiological functions in our body.

There are some elements in our body system e.g. sodium, potassium, etc., which perform the important metabolic function in the natural system of life. This function depends on the electric charge distribution within a macromolecule and interaction with its neighbors. Simple free atoms like H, N, etc. possess a centrally symmetric charge distribution. What it means is that the centre of the spherical negative electron charge distribution around the nucleus and that of the plosive charge distribution inside the nucleus are coincident. Thus symmetrically for the total atom the total charge at the internal centre of symmetry of the atom is zero. But this simple situation may not hold for some molecular and a macromolecular situation. There the resultant charge distribution may not have a centre of symmetry. The positive and negative charge centers of the system may be displaced by a small displacement d of around a 100–1,000 nm (nano meter) in scale. In case of two charges, q (one positive and one negative) having one dimensional symmetry (+ and −) separated by a distance d the electric dipole moment is written in magnitude as p = qd. Its direction is taken from negative to positive charge. In a molecular situation generally it is the volume of the molecule that is important.

If the charge distribution is spherically symmetric (but the positive and negative caters displaced) the dipole moment is expressed as, p = ε_oα E_o. Here α is the polarizability of the molecules, ε_o is a constant determined by the dielectric (electrically insulating property of the medium in which the molecule is present) constant and α = 4πa³, where a is an effective radius of the molecule (assuming as if it were a sphere), and E_o, is the local electric field, crated by the separation of + and − charges. Thus the polarizability of a molecule to acquire a dipole character depends on its volume. However there can be situations where the centre of positive and negative charges are coincident but the charge distribution itself is not spherically symmetric. It is seen that in those cases the nuclear charge distribution adopts an oblate (flattened at the poles) or a prolate (elongated at the poles) charge distribution leading to nuclear quadrupole moments of negative and positive sign respectively. In the presence of an external axially symmetric electric field gradient it is seen that the quadrupole moment, causes a precession of the angular momentum and splitting of the nuclear spin (dipole magnetic) levels. This can happen even in the absence of an applied magnetic field. This is the effect observed in nuclei with spin I ≥ 1.

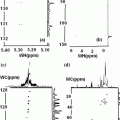
Unfortunately the concentration in the brain of quadrupole nuclei is too low. It produces a very week electrical signal in MRI. In MQ-MRI the signal produced is even weaker. There lies the challenge to the Sodium Multi-Quantum MRI in particular and the electric–magnetic analysis of the events happening in our brain. There are chemical elements of interest in the human body science which are electric–magnetic in character. These are nuclei with spin I > 1/2. The scientific meaning of spin >1 is that these nuclei also possess, an electric quadrupole moment in addition to the magnetic dipole moment. The readers who are interested in looking at detailed practical examples of quadrupole nuclei in action are referred to the Appendices A, B and A1. The Appendix are included for those readers who wish to have some familiarity with the phenomenological mathematics of the interactions between electric field gradient in which a quadrupolar nucleus is present and the magnetic dipole moment which controls the direction of these interactions. It is shown how these interactions lead to the splitting of the central core I = ±1/2 spin structure into the detailed, −3/2, −1/2, +1/2, +3/2, structure. The Figs. 79 and 80 (Appendix B1), demonstrate details about the new emerging spectroscopic details in the electric quadrupolar and dipolar magnetic scenario which can be observed by the RF spectrometer. In a multi-quantum sodium imaging approach one would be looking how to translate the microscopic detail into an imaging structure. One should note that the positive and negative electrical charges behave in nature quite differently than the two magnetic poles (north (N)–south(S)) of a magnet. We know electrical charges (+ an −) can exist independently. But the two N–S poles of a magnet can not be separated. They always exist in nature together. It is a dual magnetic character. i.e. a magnetic dipole. Electrical charges are the basic routes of communication of signal in human body. They are also the basic carriers of energy from one point to the another e.g. the metabolism. When a positive and a negative charge are bound together say e.g. in a molecule like water we call it as an electric dipole. But in a macromolecular situation e.g. tissues in our body there can be four charges (two positive and two negative) in a bound state. They are called as electric quadrupoles.

Why nature has given the freedom to electric charges (+ and −) to have multi-pole character and as well to exist independently and not to the magnetic poles (N–S)? There are many unanswered questions in the maintenance of life which nature has created. To find a real answer one need to have a strong desire to go and find out why? This will mount to carry out a curiosity (basics) driven research. But there will be some unwanted cost involved in it. The second answer is to say that nature wanted it like that. This easy way out is much cheaper. There is a saying in Australia why fix something if it ain’t broken. What it means is why worry about something that does not affect us. It is not surprising that more often than not ignorance is the preferred path chosen today. Unfortunately one needs not only financial resources (plenty available in many nations) but also the will power (not so easily available) to do the required scientific research. One need to involve many on a wider intellectual scale to find out why electrical charges and magnetic dipoles do what they do in our brain. At the moment we are busy in simpler alternatives i.e. the sports, entertainment, etc. These are the much easier outlets for the young minds and are so good economic engines. It is cheaper to stay ignorant about what goes inside our body and mind. Why worry about what happens in the future. The future will take care of itself. The oil spills in oceans, the fuel emissions in air, climate change (if there is something like that), etc., need not bother us; they will take care of themselves. Leave with nature to work out.

One may ask why not use electrical quadrupole nuclei which are much larger in number in our body, than the magnetic dipole nuclei which are so few in our body. Moreover quadruple nuclei are more intimately linked to the moment to moment and detailed spatial activities than are the magnetic dipole nuclei. The answer is that 1/2 spin nuclei exhibit a pure dipole magnetic character and are much easier to handle. The conventional MRI technology has used magnetic dipole nuclei over decades quite well. It is important to note that 75 % of NMR-active nuclei are quadrupolar and of these the vast majority are multiple half (3/2, 5/2,) and integer (0, 1, 2,) spins. Even if there are a number of convenient 1/2 spin nuclei available we can not hope to obtain a full structural picture inside our brain if we ignore all the atomic species that have quadrupolar nuclei. Many otherwise useful spin-1/2 nuclei have inconveniently, low natural abundance. For example ¹³C (magnetic dipole) has 1.1 % natural abundance (see Appendix 24 in this regard) and ¹⁵N (magnetic dipole) has 0.037 % natural abundance. If one were to study the structure of a naturally occurring solid protein one has the option of using the low-abundance nuclei or the ¹H if one restricts to using spin-1/2 nuclei. One could in fact use the ¹⁴N (100 % abundance) quadrupolar (I = 1) nuclei. NMR studies of quadrupolar nuclei can provide valuable biochemical information. Using NMR of quadrupolar nuclei one can identify and characterize cation or anion binding sites on biological macromolecules or molecular aggregates. It is possible to follow how these binding sites become modified in the course of a biochemical reaction of transformation. NMR allows to determine metal ion populations of individual binding sites of a multiple protein.

The relaxation of quadrupolar nuclei are usually determined by their interaction with fluctuating electrical field gradients at the site of the nucleus. NMR can provide insight into ion binding to highly charged molecular aggregates or polyelectrolytes. It is seen that if we exclude the most commonly used magnetic nuclei (e.g. hydrogen/proton in water) then NMR sensitivity observed is too low. It can be even lower than the lowest known. The lowest known is that experienced for the ¹³C nuclei (see Appendix 14.3.24) which are normally avoided in MRI. The low sensitivity is in reference to the six essential element nuclei: ³³S, ⁴³ Ca, ⁵³Cr, ⁵⁷Fe and ⁶⁷Zn. The I = 1/2, nuclei are generally considered to be much easier to handle than nuclei with I = 3/2 which possess electric quadrupole moment. However in biological systems the prospects of studying I = 1/2 nucleus like ⁵⁷Fe (see Appendices A22 and A23, in relation to the Alzheimer disease) is limited. One should realize that diamagnetism (magnetic dipoles) is instantly created when a magnetic field is applied as a shield (reaction) to the applied field. On the other hand paramagnetism is a permanent feature naturally preset in a molecule. Some molecules are natural magnets (paramagnets). The applied field only tries to align them in its own direction. The occurrence of paramagnetic relaxation will also add to difficulty of observing I > 1/2 nuclei like ⁶³Cu, ⁶⁵Cu in Cu₂⁺ complexes, etc. For quadrupolar nuclei (I > 1/2) evaluation of the experimental situation is more complicated than for I = 1/2 nuclei.

There is occurrence of the non-exponential relaxation (refer to Appendix A3, A17, A26 and A27 for some Na and K examples) of the atomic and nuclear excitations of the quadrupolar nuclei by the RF pulses. It is seen that the second order dynamic frequency shifts (offsets of the resonance frequency in time) are some of the problems (see Appendix A2 for the basics involved) which need further insight. Quadrupole relaxation is caused by the interaction of a nuclear electric quadrupole moment with fluctuating electric field gradient at the place of the nucleus. Electric field gradients are system dependent properties and may be regarded as either intramolecular or intermolecular in origin. The aim behind writing this book is not to create just another text book in the field of MRI. The idea is to make the medical professionals (MPs) aware of what goes behind making an MRI picture and how well they can make use of it in the diagnostics of human brain disorders. The education about sodium imaging using multi-quantum coherences at the molecular level is the main theme of the book. This awareness is carried out by including practical illustrations from recent clinical studies.

The explanation of the connections to the basics of the fundamental quantum chemistry involved among the macromolecules is included as part of the illustrations. Detailed mathematical and phenomenological treatment is avoided. We have given some glimpses of the practical approach used in the book through demonstration of practical examples. A typical example of an illustration is a study of an ischemic tissue in the brain. It sets an example of the basics involved for a reader. An accurate concentration gradient of sodium and potassium ions across a membrane between tissue and the free surrounding ion environment is maintained by a healthy tissue in a specific pattern by natural forces. In an ischemic situation this gradient is disturbed. It leads to an unpredictable and erratic electric field gradient around the tissue. The result is that the I = 3/2 quadrupole (electric)-magnetic (dipole) moment character of the nucleus breaks (the degenerate spectral energy level character) into multiple (four possible) spectroscopic transitions (14.3.32–14.3.34 for mathematical details). These transitions carry with them the information about the abnormal behavior of the region of interest (ROI).

A scientist uses his or her professional, physics, chemistry and mathematics (PCM) skills to design,a suitable RF (radio frequency) pulse structure to excite the molecules in a ROI (region of interest). Then one develops suitable parameters of detection in the MRI machine to produce results to the desired level of perfection. This finally leads to the MRI picture we see. Efforts are made in this book for the reader to enable to learn about all the methodologies that have evolved involved in as simple a manner as possible. Though the book is aimed at improving continuous education of the clinical doctors through presentation of illustrations of conceptual pictures, etc., other professionals working in the field of medicine and science will find it equally interesting. The PCM education experts are now exposed to new challenges ahead. They have to simplify the research and development results created by the MRI researchers. PCM professionals have on their hand a duty to develop simplified versions of the MRI literature essential for the future user generations. There is a decline in education at the grass roots level about science among the much wider community today. One will always see further developments in the MRI technology. Coming generations will face a missing gap to handle further advancements.

There will be a limited supply of scientific manpower world wide very soon to handle the disasters both due to natural causes and the technology created. Oil spills in the ocean and the fuel emission in the air, etc., are here to stay. Are we developing suitable and enough, the scientific know how, the intellectual human resources to be able to handle the inevitable, the much worse disasters bound to come? This book is written specifically to enhance knowledge of the medical professionals working in the field of the applications of MRI to the area of medicine. The technology of MRI offers opportunities to visually see the events happening in real time, e.g. in a tumor in the brain. The standard techniques employing chemical shift imaging in a broader voxel (mm³ to cm³) using echo planar imaging (EPI) is common place in the routine MRI diagnostics of the brain disorders.

There is a recent change in approach in the MRI technology to use micron μ (10⁻⁶ m)³ to mm³ size volumes for closer scrutiny of the events happening in space and time e.g. in a tumor. This is called as the quantum (more precisely the multi-quantum) magnetic resonance imaging i.e. the MQMRI. The reason why it is called as the MQMRI is that now one is looking at the atomic and molecular level the details of the multi-quantum interactions between atoms in molecule and the molecular–molecular interactions on a finer scale (<mm) of imaging. The quantum structure of events happening is truly revealed in MQMRI while in the conventional MRI it gets smeared out. The conventional MRI treats the magnetic spins of the electron-atom system as a single quantum system. What it means is that the atomic magnetic moments are assumed all identical in a voxel. The variable response to the applied static magnetic field applied along the z-direction and the RF (radio frequency) magnetic field applied in the x–y directions is due mainly to the different dispersive character of the spins because of the specific medium in which they reside. The fine atomic-nuclear quantum structure possessed by the tissue does not come into the picture.

In order to work out the real chemistry of the region discrete quantum level signal from a narrow region should form part of the detailed imaging. We want the book not to become too diverse in its character. The scope of the book is directed towards quantum coherence imaging and its applications to understand the human brain science. The development of the book surrounds imaging as the nucleus. The associated knowledge of the PCM required is provided in as simplified manner as possible as an induction to the reader to be able to make a better use of the MRI picture. The nuclear magnetic resonance imaging (NMRI) is basically in conceptual matter very identical to the atomic case. The major difference is the magnitude of the nuclear dipole-magnetic moment is about thousand times smaller than the atomic one. This is because a neutron or a proton is thousand times heavier that the electron. But there are some other subtle differences. The authors feel that this is not the right place to go into the details about atomic and nuclear physics involved behind the MQMRI. The reader is referred to a standard text book in this matter. But a summarized account forms part of this book in the following sections.

Our brain is a complex structure of atoms, molecules, macromolecules, etc. An atom has a fundamental magnetic dipole moment generated due to the valence (outermost) electron in orbit around the nucleus. Identically a nucleus also exhibits a resultant magnetic moment due to the circulating neutron and proton electric currents inside the nucleus. There is also a magnetic moment associated with the intrinsic electron rotation about its own axis. Fundamental to all these components of dipole magnets is the angular momentum of rotation. In the case of an electron its angular momentum is represented by the quantum selection rule, S = ±(1/2)ħ. In an atom, S, combines with the angular momentum due to an electron in an orbit, L, to produce the resultant angular momentum, J = L ± S. L can have simplified quantum states of 0, ±1, ±2 in the presences of an applied static magnetic field in the z-direction. But S has only two quantum state ±1/2. The corresponding resultant J magnetic moment will also have a well defined quantum structure depending upon the quantum selection rules due to spin (electron)—orbit (atom) interaction within an atom. In an ensemble of atoms, molecules, etc., a multi-particle resultant quantum structure will be established with its own set of selection rules. The nucleus has a well established magnetic order of its own. A nucleus is buried deep inside the atom and relatively free from the atomic perturbations. The situation is quite similar but quite different in the magnitude of the magnetism and its quantum structure. In the nuclear case we have a different spin structure of the magnetic states. We can have 1/2, 3/2, 5/2,.. etc., states. We can also have integer values 1, 2, 3, …. What multiple quantized states, for the overall atomic-molecular magnetic system can have is decided by the overall quantum selection rules.

An interested reader for a detailed account need to refer to a standard text book in physics, e.g., [2], in this matter. Only the final results will form part of discussion here. A nucleus can have higher diamagnetic quantum energy states, e.g. ±3/2, ±5/2, etc. due to the peculiar charge distribution (e.g. the quadrupole charge distribution) around the centre of the nucleus. Nuclear magnetic moment is also a magnetic moment arisen analogous to the atomic one. A nucleus can have magnetic moment = 0, 1/2, 1, 3/2 ….The origin of the magnetic dipole moments for a nucleus has, protons and neutrons circulating currents, inside the nucleus. It is similar to the atomic case. The exact explanation of the mechanism of the processes involved in detail is beyond the scope of this book. A brief summary as follows should prove useful for the reader. The reader is reminded that the importance of the knowledge about the overall macromolecular quantum structure is the key factor that controls the imaging structure in a voxel. The, contagious data recorded from voxel to voxel allows the overall picture of the brain, produced. We wish to point out here that not all the electrons in orbit in an atom contribute towards atomic magnetic moment. It is only the odd numbered electron in the outermost orbit usually called as the valence electron that makes a debut. This is also chemically the most active electron and is responsible for creating binding between atoms to produce molecules and macromolecules. The inner-orbit electrons cancel their magnetic moment as pairs up and down. The situation in the nuclear case is similar. Here the odd numbered (unpaired) neutrons and protons produce the nuclear magnetic dipole moment. Also one should note that not all the chemical elements in the periodic table have a dipole-magnetic moment and not all diamagnetic-quadrupole nuclei are present in our body health system. Why is it so?

A nucleus has a complex structure made of neutrons and protons. The total magnetic moment is the combined effect of intrinsic magnetic dipole moments of neutrons and protons. The magnetic moments of most nuclei have been accurately determined in the laboratory (see Appendices A1) for nuclei important to human body. It is done by measuring the hyperfine splitting in the spectroscopy of an atom-nucleus system due to the hidden degeneracy present. This degeneracy in the, nuclear-atomic system dipole magnetic moment arises as a result of an internal magnetic field exerted on the electrons by the nucleus. The magnitude of this interaction between the atomic electrons and the nucleus is expressed in the form of an interaction energy ΔE. Its value depends, upon the orientation of the nuclear dipole magnetic moments in the presence of the internal magnetic field. It can in a descriptive manner be written as ΔE_N ~ C_N[f_GT(f_GT + 1) − i_N(i_N + 1) − j_A(j_A + 1)]. Here the symbols j_A, i_N, and f_GT have their importance as follows. j_A = the quantum numbers in regard to the magnitude of the atom’s total electronic (electron plus atomic orbital) angular momentum; i_N = the quantum number corresponding to the total nuclear angular momentum; f_GT = the quantum number obtained as result of the resultant, worked out from the atomic and the nuclear quantum numbers. Here C_N is a constant which is proportional to the magnitude of the nuclear magnetic dipole moment.

We feel the presentation of knowledge through mathematical symbols, should prove very effective. It is easy to remember something new if it is associated with, a symbol, a process or a result. By measurements experimentally it has been verified that for all nuclei the most fundamental dipole magnetic nuclear magnetic moment is given as μ_N = (eħ/2M_P) = 5.05 × 10⁻²⁷ amp-m². Here e is the electron (or proton) charge, ħ is the Planck’s (angular) constant and M_P = the mass of the proton. All the quantitative nuclear magnetic moments are expressed as an integral multiplication of it. This fundamental (nuclear) dipole magnetic moment in the physics world, is referred to, as the nuclear magneton. The magnitude of nuclear magnetic moment in each case, is worked out, by experiments through, measurement, of the nuclear hyperfine splitting of the magnetic dipole energy levels. The sign of μ_N can be positive in some cases and negative in others. It is found that for the nuclei with both atomic mass number A (total mass equivalent number of the neutrons and protons) and the atomic number Z (equal to the total number of protons in the nucleus or the total number of electrons in the orbit of an atom), being even, μ_N = 0. The total nuclear angular momentum quantum number i_N, sometimes referred to as the nuclear spin can be obtained from an experiment simply by counting the number of energy levels of hyperfine splitting multiplet. If the multiplet is associated with a value of j_N, larger than i_N, then f_N can assume (2i_N + 1) different values. It results into (2 i_N + 1) different energy levels. It is also found that, i_N is an integer, for nuclei of even A, with i_N = 0, if Z is also even. But i_N is a half integer for nuclei of odd A.

The magnitude, I, of the total nuclear angular momentum is given in terms of i_N as, I = √[i_N(i_N + 1)]ħ, i_N, bring the quantum number corresponding to the total nuclear angular momentum. The total angular momentum of a nucleus arises from the intrinsic spin angular momentum of its protons and neutrons, and also from the orbital angular momentum due to the motion of these particles within the nucleus. It is also important to point out here that in the nuclear case the word spin frequently refers to the total angular momentum of a nucleus in contrast to the atomic case. In the atomic world the word spin refers to the intrinsic spin angular momentum of the electron. We wish to say here that the reader who is not able to comprehend the simple descriptive mathematics as presented here need not really bother about it. The, presentation is purely to perceive a connection between what is observed and why it is observed in an MRI picture. It is done in round about quantitative but yet in a descriptive manner. The above logical deductions for the nuclear case have in fact been made in analogy with the case of electron spin and the atomic orbital angular momentum and have been verified experimentally. It is, considered appropriate here to shed some more light as below on the atomic case itself. In the atomic case there are two types of spins. One is the intrinsic spin of the electron around its own axis, referred to in the MRI literature by the symbol S. The other is the orbital angular momentum of the electron motion around the nucleus. It is referred to by the symbol L. Each of these are randomly oriented in space except for a small order created by the internal nuclear magnetic field present in the ensemble. This field is naturally present around a nucleus. It is local in nature in a confined environment like our brain as a result of ensemble of group of atoms, molecules, etc.

The multi-particle electron spin resultant is expressed as, S′ = √[s′(s′ + 1)]ħ and the atomic angular momentum as, L′ = √[l′(l′ + 1)]ħ. These magnitudes in real atom situations, e.g. Hydrogen, Potassium, etc., have been worked out through the rules of quantum mechanics (QM) and experiments. This book is not the right place to go into details of the quantum mechanical selection rules. The reader is referred to a standard text book in physics, e.g. [1–3]. It, should suffice here to include description as a helpful conceptual matter for a reader as follows. We, should remember that in an enclosed space like our brain the atoms and molecules are free to participate, coherently, in any function or activity in the brain. They behave collectively in a small volume say a voxel. Thus it is a multi-particle system in operation. But to have a coherence in space and time a regional force is required. This regional force, is provided by the electron-nuclear, electric–magnetic field, provided by the bound, electron and nucleus, system. In the absence of an external magnetic field a quantum number say, l′, can have values, √l′(l′ + 1), in space. This is the three dimensional quantization with very-many possible orientations for the spins. One can see that, l′ an s′ are the quantum numbers with permitted integer values 0, 1, 2, ….

The three dimensional projection with various components in space is reduced to a two dimensional structure on the application of the external, static magnetic filed. This is to reduce, the number of possible components. However a quantum number say for example, l′, would be restricted to values l_z′ = 0, ±1, ±2, etc. in the presence of, an externally applied static magnetic field H_z. This is the simplicity achieved in the situation. A factor of the type, √l′(l′ + 1), l′ = 0, 1, 2, …, often appears before the magnitude of any angular momentum. It specifies in free space the quantized angular (oriented) positions of the individual angular momentum. Its direction, is perpendicular, to the plane of the rotational orbit, and acting, through the centre, of the orbit e.g. in an atom. S′ and L′ are the angular momentum in reference to the multi-electron and multi-particle system. This is the situation we have in our brain. These further combine, to produce a resultant, J′ = L′ + S′. The J′ logically is expressed as, J′ = √[j′(j′ + 1)]ħ. Here j′ are represented as quantum numbers 0, 1, 2, … for the resultant local (say a macromolecule) system. In a magnetic field however it takes up the simplified values J_z′ = m_z ħ, ħ, being the angular Planck constant, and m_z = 0, ±1, ±2, …etc. The reader is reminded, that the L–S (the two angular momentum) coupling, which results into the resultant J, makes the basis of J-coupled imaging, in a real MRI situation. In the atomic case the L–S (often referred to as the spin–orbit interaction) results into a spectrum of energy levels given as, ΔE = (μ_b B g m_z′). Here μ_b is the fundamental dipole magnetic moment[2] due to an electron in an atom, given as μ_b = (eħ/2m_e). The symbol e = the electrons’ charge, = 1.6 × 10⁻¹⁹ C, ħ = the familiar angular (ħ = h/2π) Planck’s constant, = 1.055 × 10⁻²⁴ J/s, and m_e is the electron mass, = 9.109 × 10⁻³¹ kg. Upon substitution, one gets μ_b = 0.927 × 10⁻²³ amp-m². It is often referred to as the atomic Bohr magneton. The symbol B (the symbol B and H are interchangeably used in the MRI literature) is the static magnetic field. Internally, some B, is naturally present, around a nucleus, in a natural ensemble, like our brain.

It is interesting to note this internal magnetic field is expected to be of the order of 1 T, in free space. One should compare it with 3 T magnetic field normally used in MRI machine. This internal magnetic field which the nature has created locally around a nucleus (or macromolecule collectively) in our brain is capable of creating a local order. The natural local magnetic order though experimentally very difficult to observe creates the local network of electrical circuits used by the brain to carry on communications between different channels of the brain, e.g. metabolism, functionally mediated blood flow, etc. The reader is reminded that in MRI we just suppress the local order and superimpose an order of our own by applying a much stronger (3–7 T) static magnetic field B externally. We can work out very well the intricacies of the static order we have imposed in the brain. Further, the excitation of the molecules by an external RF (radio frequency) field leads to the generation of the electrical signals we receive back. It give us all the information about what is happening, in the brain in a selected region during a particular interval of time. The reader may have realized that we have not yet completely defined the symbol g which appears in the interaction energy between the magnetic dipole and he applied field B. Mathematically it can be written as, g = [1 + ({j′(j′ + 1)}} + {s′(s′ + 1)}} − {l′(l′ + 1)}})/2{j′(j′ + 1)}].

In the presence of the external or internal magnetic field the J′, L′, S′ have two-dimensional space quantization (orientation in space). It is controlled such that instead of the j′, l′, s′, following the quantum numbers, 0, 1, 2,…, they reduce to their, z-component values only. These are called as the magnetic quantum numbers as, m_z = 0, ±1, ±2, ±,…Now the general J′, L′, S′ take on specific z-resolved, magnitudes as, J′ = m_jz J_z, L′ = m_lz J_z and S′ = m_sz J_z, respectively. The reader is reminded here that for the sake of simplicity the z-components (sometime refereed to as the azimuthal quantum numbers), m_lz, m_sz and m_jz are referred to as if having the allowed same integer values. In a real situation they will follow different specific selection rules, in different situations. The reader is reminded that symbols with the superscript are for the multi-electron system. The symbols without mean the case of a single particle. The exact spectrum energy structure for any atom can be built from an observed experimental spectroscopy, with appropriate selection rules [2]. A simplest illustration as an example is, Δs′ = 0, Δ_l′ = 0, ±1, Δ_j′ = 0, ±1 (but not j′ = 0 to j′ = 0). The symbol Δ means a change in quantum number in a transition from one energy state to another. These, are only, illustrative values, to impress upon the reader the type and the complexity of the conceptual matter, involved. A detailed knowledge [2] is required for the actual situations. Before, proceeding further it is important to mention as follows. If education about simple quantum mechanical concepts for a learning purpose is introduced as part of education curriculum at the secondary school education system then it will become easy for the professionals to assimilate new developments later, in their life.

An atom has a cloud of negatively charged electrons surrounding the positively charged nucleus. Taking everything to be spherically symmetric with the nucleus at the centre and the centre of gravity of the total + charge coincident with that of the total − charge the whole atom would spatially and electrically be neutral at the centre. But in some situations the centre of gravity of the negative charge around the nucleus may not be coincident with the centre of the positive charge at the centre of the nucleus. In such circumstances the atom is said to behave as an electric dipole. The hydrogen molecule in this circumstance presents a good example. Also when charges are present as an ensemble like in the case of macro-molecules in a tissue the charges try to associate themselves in a minimum energy configuration as surface charges rather than line charges (electric dipoles). The result is the formation of higher order poles. Electric quadrupole structure is often observed in many molecules. The result is that the nuclei do not just have ±1/2 ћ magnetic dipole energy states. The presence of quadrupole nuclear charges around can excite the nuclear magnetic dipole states to higher energy states, ±3/2 h, ±5/2 h, etc. The nuclei within a molecular structure can have more complex charge distribution structure, e.g. an ellipsoidal distribution of electrical charges in space. This deviation of charge distribution in a nucleus from perfect spherical symmetry has some natural consequences.

It is observed that the doublet magnetic dipole magnetic structure may have a further finer structure. This is contributed by the electric quadrupole charge structure. The new structure is partly a result of electric charge interaction between an ellipsoidal nuclear charge distribution and the internal (intrinsic) electric field present around the atom. The overall orientation of the quadrupole electric field in space is controlled by the orientation of the nuclear magnetic dipole moment which is controlled by the magnetic field internal (naturally present in the brain) or external. The observed departure of the nuclear charge distribution from spherical symmetry is specified by the nuclear electric quadrupole moment q. For q > 0, the ellipsoidal charge distribution, is elongated, in the direction of, its symmetry axis. The elongation increases as the q becomes more positive. For q < 0, the ellipsoidal charge distribution is flattened in the direction of the symmetry axis. The flattening increase, as q becomes more negative. For nuclei with spin i ≥ 1, the hyperfine splitting, measurements show that there are cases with electric quadrupole moment q > 0 as well as with q < 0. For nuclei with dipole magnetic moment, i = 0 or i = 1/2, the measurements always yield q = 0; that is no departure from spherical charge shape are observed for such nuclei.

One should realize that a nucleus seems to have spherical charge distributions shape if it has zero nuclear spin. In this case it does not have any particular orientation in space since there is no total angular momentum vector that must maintain a fixed component in some direction. The nucleus can be thought of assuming in very rapid succession all possible orientations in space. Even if it is actually non spherical in shape one may not see this in the hyperfine splitting measurements. Hyperfine splitting and most other observable effects depend on the time average of the nuclear shape. To put it in another way most measurements, simply do not have the time resolution required to detect the instantaneous nuclear shape. But measurements involving nuclear reactions do. In fact it is seen that many nuclei with nuclear spin, i = 0 actually are nonspherical although this can not be seen by hyperfine splitting. More complicated symmetry arguments prove that nuclei must also be observed to be spherical in hyperfine splitting and other time-averaged measurements if they have nuclear spin 1/2. The largest values of q are found for the nuclei in the region of the rare earth elements. In the most extreme case the largest dimensions of the ellipsoidal charge distribution is along the direction of the symmetry axis and it exceeds the smallest dimension by about 30 %. But for typical nuclei with i ≥ 1, the difference in the largest and the smallest dimensions of the ellipsoid is only a few percent. So for most purposes it is a good approximation to assume that typical nuclei are spherical particularly since more than half of all the nuclei have i = 0 and so they appear in most circumstances to be precise spherical.

We have discussed above that the electric quadrupole moment q is a measure of the departure of spherical symmetry of the nuclear charge distribution as observed in measurements. An example is hyperfine splitting which is sensitive to the time average of this departure. The exact definition of the electric quadrupole moment is q = ∫ ρ[3z² – (x² + y² + z²)]dτ. Here ρ is the time averaged nuclear charge density in units of proton charges. The three-dimensional integral is taken over the nuclear volume with small volume dτ, taken as initial, small volume, element. One should note that q (charge) is equal to Z, the number of protons in the nucleus, multiplied by the average over ρ, of the difference between three times the square of the z coordinate, and the sum of the squares of all the coordinates, x, y, z. That is q = Z[3 < z² >  – (< x² > + < y² > + < z² > ]. One can see then, that q = 0, if the time averaged nuclear charge density ρ is spherically symmetrical, since in that case, x² = y² = z². If ρ is not spherically symmetric, it must at least have an axis of symmetry, along the direction, about which, the total angular momentum, of the nucleus, randomly processes, as time passes. In typical cases, the time averaged charge density, is an ellipsoid, with a symmetry axis, in ellipsoid direction. In the above equation the symmetry axis is taken as the z-axis. The equation demonstrates that for q > 0, ρ is elongated in the z-direction since then, [< z² >] > [< x² > + < y² >]. On the other hand when q < 0 ρ is flattened in the z-direction so that, [< z² >] < [< x² >} + [< y² >].