(1)
Amersham, Buckinghamshire, UK
7.2.1 b ≪ ra
7.2.2 b ∼ ra
7.2.3 bmin < b < bmax
7.2.4 b > bmax
7.3.1 Energy Transfer, Q
7.3.2 Momentum Transfer, q
7.6 Media
Abstract
This chapter introduces us to Part III, which investigates the mean collision energy loss resulting from the interactions between moving charged particles and matter. Most importantly, it draws the distinction between the definitions of soft and hard collisions which will dominate the first three chapters. It will also present considerations of complex media which will become of interest later in Part III.
The theory gives a satisfactory description of the influence of impacts for which the minimum distance b between the electron and the passing particle is larger than the atomic dimensions. Quantum mechanical corrections have to be introduced for the very close impacts, when the particle passes through the atom.
–Enrico Fermi (1940)
7.1 Introductory Comments
Excluding the hadron–nuclear interactions based upon the strong nuclear force, charged particles interact with the atoms in the medium they are traversing through via the Lorentz force , 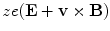 . In Part II, we investigated those interactions defined as being elastic, i.e. those that are within our definition for which the sum of the projectile and target kinetic energies are equal before and after the scatter. It should again be emphasised that these elastic collisions also include those within which kinetic energy is lost by the projectile and transferred to the medium. This energy transfer is manifested as the recoil energy of the target. As another example, if the energy transfer from the projectile to an atomic electron during a Coulomb scatter is much greater than the electron binding energy, the pre-collision electron can be considered to be quasi-free and stationary with the result being that the collision can be treated as being elastic. Energy throughout both collisions has, by definition, been transferred to an atom within the medium. For the case of the target being an atomic electron, this particle-atomic electron collision is known generally as a hard collision 1 and will be the subject of Chap. 9. Such an interaction requires the penetration of the projectile to within the atomic electron ‘cloud’ followed by a direct and singular collision with one electron. The collision between projectile and electron is thus to be described quantum mechanically. It is inherently obvious that such a case of proximity is unlikely, whereas the interaction of the target with the entire atom at a distance has a greater probability of occurring. This latter condition is referred to as a soft collision, the subject of Chap. 8, as the magnitude of the energy transfer is reduced.
. In Part II, we investigated those interactions defined as being elastic, i.e. those that are within our definition for which the sum of the projectile and target kinetic energies are equal before and after the scatter. It should again be emphasised that these elastic collisions also include those within which kinetic energy is lost by the projectile and transferred to the medium. This energy transfer is manifested as the recoil energy of the target. As another example, if the energy transfer from the projectile to an atomic electron during a Coulomb scatter is much greater than the electron binding energy, the pre-collision electron can be considered to be quasi-free and stationary with the result being that the collision can be treated as being elastic. Energy throughout both collisions has, by definition, been transferred to an atom within the medium. For the case of the target being an atomic electron, this particle-atomic electron collision is known generally as a hard collision 1 and will be the subject of Chap. 9. Such an interaction requires the penetration of the projectile to within the atomic electron ‘cloud’ followed by a direct and singular collision with one electron. The collision between projectile and electron is thus to be described quantum mechanically. It is inherently obvious that such a case of proximity is unlikely, whereas the interaction of the target with the entire atom at a distance has a greater probability of occurring. This latter condition is referred to as a soft collision, the subject of Chap. 8, as the magnitude of the energy transfer is reduced.
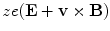 . In Part II, we investigated those interactions defined as being elastic, i.e. those that are within our definition for which the sum of the projectile and target kinetic energies are equal before and after the scatter. It should again be emphasised that these elastic collisions also include those within which kinetic energy is lost by the projectile and transferred to the medium. This energy transfer is manifested as the recoil energy of the target. As another example, if the energy transfer from the projectile to an atomic electron during a Coulomb scatter is much greater than the electron binding energy, the pre-collision electron can be considered to be quasi-free and stationary with the result being that the collision can be treated as being elastic. Energy throughout both collisions has, by definition, been transferred to an atom within the medium. For the case of the target being an atomic electron, this particle-atomic electron collision is known generally as a hard collision 1 and will be the subject of Chap. 9. Such an interaction requires the penetration of the projectile to within the atomic electron ‘cloud’ followed by a direct and singular collision with one electron. The collision between projectile and electron is thus to be described quantum mechanically. It is inherently obvious that such a case of proximity is unlikely, whereas the interaction of the target with the entire atom at a distance has a greater probability of occurring. This latter condition is referred to as a soft collision, the subject of Chap. 8, as the magnitude of the energy transfer is reduced.
. In Part II, we investigated those interactions defined as being elastic, i.e. those that are within our definition for which the sum of the projectile and target kinetic energies are equal before and after the scatter. It should again be emphasised that these elastic collisions also include those within which kinetic energy is lost by the projectile and transferred to the medium. This energy transfer is manifested as the recoil energy of the target. As another example, if the energy transfer from the projectile to an atomic electron during a Coulomb scatter is much greater than the electron binding energy, the pre-collision electron can be considered to be quasi-free and stationary with the result being that the collision can be treated as being elastic. Energy throughout both collisions has, by definition, been transferred to an atom within the medium. For the case of the target being an atomic electron, this particle-atomic electron collision is known generally as a hard collision 1 and will be the subject of Chap. 9. Such an interaction requires the penetration of the projectile to within the atomic electron ‘cloud’ followed by a direct and singular collision with one electron. The collision between projectile and electron is thus to be described quantum mechanically. It is inherently obvious that such a case of proximity is unlikely, whereas the interaction of the target with the entire atom at a distance has a greater probability of occurring. This latter condition is referred to as a soft collision, the subject of Chap. 8, as the magnitude of the energy transfer is reduced.In Part III of this book, we will look specifically at those charged particle–matter interactions which transfer kinetic energy to the medium, either through inelastic processes or through, as described in the previous paragraph, what are effectively elastic knock-on collisions between a projectile and an atomic electron target. As noted in Part II, the types of collisions are differentiated into what Bohr (1948) defined as nuclear collision, in which the projectile interacts with the atom as a whole, and an electronic collision which is that between the projectile and an atomic electron . The former would be largely inelastic (unless the transfer of the projectile’s kinetic energy greatly exceeds the binding energy of the electron), resulting in atomic excitation or ionisation with the ejection of low-energy electrons (and the sum of the post-collision kinetic energies being less than that which existed pre-collision), whereas the latter, as previously noted, is an effectively elastic interaction. These categories are analogous to the terms most commonly used in medical radiation physics: soft collision and hard collision, respectively. We will use the latter categorisations because of their common use in our discipline.
The differentiator between soft and hard collisions in the classical theory is the magnitude of the impact parameter which describes the proximity of the projectile’s trajectory to the atom, the atomic electrons and the atomic nucleus. Within each category, different physics occurs which we now discuss. In order to set the stage, Fig. 7.1 shows the regions that we shall consider.
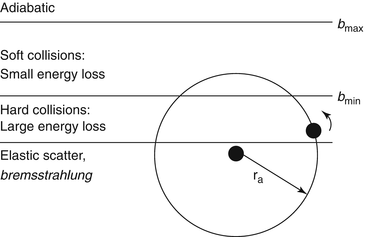

Fig. 7.1
Conceptual differentiation between projectile–atomic target interactions on the basis of impact parameter
At small impact parameters, the projectile interacts directly with the atomic nucleus with the consequence of elastic scatter as described in Chap. 5 or, for an electron or positron projectile, bremsstrahlung. At slightly larger values of impact parameter, the projectile interacts directly and singularly with atomic electrons in elastic (or quasi-elastic) scatters (i.e. hard collisions). At even larger values of impact parameter, beyond b min, but less than some value b max, the projectile does not interact with individual electrons but with the atom as a whole via soft collisions where limited amounts of energy are transferred. Beyond a certain impact parameter b max, the projectile does not transfer energy effectively to any component of the atom and the response is regarded as being adiabatic. The above descriptions are peculiar to classical mechanics. In the quantum (Bethe) theory, the metric that differentiates between soft and hard collisions is the momentum transfer (or, equivalently, the energy transfer) resulting from the collision. However, the two metrics of classical and quantum mechanics can be considered to be related through the Heisenberg uncertainty principle, 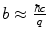 .
.
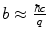 .
.Both conditions are now reviewed in the following two sections.
7.2 Soft Versus Hard Collisions: Impact Parameter Regimes
7.2.1 b ≪ ra
Let us begin by considering the case of the impact parameter being much smaller than some atomic radius, 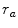 , which we use to characterise atomic size. This was, in fact, the spatial regime that we considered in Chap. 5 in the context of elastic Coulomb screening from a nucleus screened by atomic electrons. For this case of
, which we use to characterise atomic size. This was, in fact, the spatial regime that we considered in Chap. 5 in the context of elastic Coulomb screening from a nucleus screened by atomic electrons. For this case of 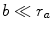 , the projectile can undergo four possible interactions:
, the projectile can undergo four possible interactions:
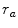 , which we use to characterise atomic size. This was, in fact, the spatial regime that we considered in Chap. 5 in the context of elastic Coulomb screening from a nucleus screened by atomic electrons. For this case of
, which we use to characterise atomic size. This was, in fact, the spatial regime that we considered in Chap. 5 in the context of elastic Coulomb screening from a nucleus screened by atomic electrons. For this case of 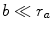 , the projectile can undergo four possible interactions:
, the projectile can undergo four possible interactions:
If the projectile is hadronic (and not necessarily charged as in the case of the neutron) and it penetrates into the atom sufficiently that its wavefunction overlaps that of the nucleons within the nucleus, there is the possibility of nuclear excitation or even fragmentation if the projectile energy is comparable to, or sufficiently greater than, the nucleon binding energies. This is, for example, the basis of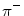 -radiotherapy as discussed in Chap. 1.
-radiotherapy as discussed in Chap. 1.
A charged projectile can interact with the nuclear protons which can lead to nuclear excitation and fragmentation.
A charged projectile can be elastically scattered by the nuclear Coulomb field with negligible recoil, as discussed in Chap. 5.
If the projectile is an electron or positron, it can interact with the nuclear Coulomb field and create bremsstrahlung.
In Part III, none of the above three interactions will be considered.
7.2.2 b ∼ ra
Let us consider the case of the impact parameter being of comparable dimensions to that of the atom. In this spatial regime, the projectile can interact directly with single-atomic electrons through the hard collisions previously noted. These interactions are described by explicit projectile–electron interaction cross sections and will be the topic of Chap. 9. We will consider the cases of the projectile being a spinless massive particle (defined as 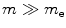 ), the electron and the positron. This spatial regime is also characterised by the inequality of
), the electron and the positron. This spatial regime is also characterised by the inequality of 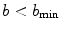 , where
, where  is the demarcation between the soft and hard collision regimes and is derived in Chap. 8. The energy lost by the projectile will be relatively high due to the close-range interaction between the projectile and the target atomic electron.
is the demarcation between the soft and hard collision regimes and is derived in Chap. 8. The energy lost by the projectile will be relatively high due to the close-range interaction between the projectile and the target atomic electron.
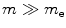 ), the electron and the positron. This spatial regime is also characterised by the inequality of
), the electron and the positron. This spatial regime is also characterised by the inequality of 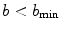 , where
, where  is the demarcation between the soft and hard collision regimes and is derived in Chap. 8. The energy lost by the projectile will be relatively high due to the close-range interaction between the projectile and the target atomic electron.
is the demarcation between the soft and hard collision regimes and is derived in Chap. 8. The energy lost by the projectile will be relatively high due to the close-range interaction between the projectile and the target atomic electron.7.2.3 bmin < b < bmax
When the magnitude of the impact parameter is far greater than atomic dimensions but still within a distance allowing the particle to interact with the atom, the projectile transfers energy, an ensemble of atomic electrons as a whole. Here, the momentum and energy transfer to the atom is reduced due to the greater distance from the atom and the larger number of electrons potentially influenced.