(1)
Amersham, Buckinghamshire, UK
Abstract
This chapter introduces us to Part IV, the subject of which is the stochastic nature of the energy loss of charged particles through collisions.
15.1 Introductory Comments
In Part III, we evaluated the energy loss and stopping power of a charged particle decelerating in a medium. The change in the particle’s kinetic energy was due to the combination of energy loss to the atom as a whole (soft collisions) and through individual collisions with atomic electrons (hard collisions). Classical and quantum theories were both considered, as were various effects that result due to the interaction of the particle and the medium. Perturbative effects reflecting the real cases of medical exposures to charged particles were then developed.
However, in all of those calculations, it has been assumed that energy loss with distance travelled is a continuous function. That is, for a charged particle that has traversed a distance t through a medium, the energy loss is calculated by integrating the linear collision stopping power over distance traversed:
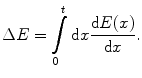
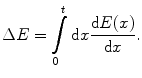
(15.1)
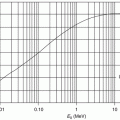
This expression is, of course, an approximation which can be considered valid for specific conditions only. We recognise that the energy transferred from the charged particle to the medium occurs through discrete interactions with atoms. Hence, the energy loss process is not a continuous one, as described by (15.1), but is, instead, stochastic, as demonstrated by Fig. 15.1.
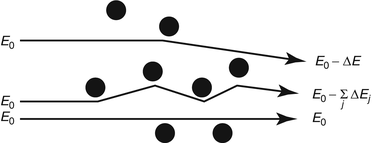

Fig. 15.1
Principle of energy straggling. A mono-energetic beam of charged particles is incident to a medium from the left. Each particle is incident to a different number of atoms at different impact parameters. The result is that the exiting beam exhibits a spectrum of kinetic energies reflecting this (Redrawn from Sigmund (2006))
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree