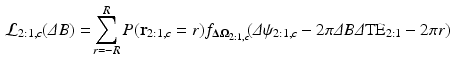could be written as:
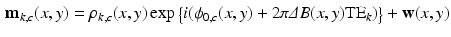
(1)
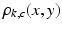 is the decayed magnitude at echo time TE
is the decayed magnitude at echo time TE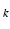 modulated by the sensitivity of channel c,
modulated by the sensitivity of channel c, 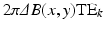 is the underlying tissue phase value and
is the underlying tissue phase value and 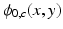 is the channel-dependent phase offset of channel c.
is the channel-dependent phase offset of channel c. 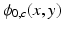 varies spatially due to factors such as the distance between the excited spins and the coil, the length of the coil’s cables, and electronic delay [9]. Strictly speaking,
varies spatially due to factors such as the distance between the excited spins and the coil, the length of the coil’s cables, and electronic delay [9]. Strictly speaking, 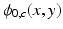 also varies with time due to drifts in frequency synthesizer and/or imperfections in the centering of k-space [5]. The term
also varies with time due to drifts in frequency synthesizer and/or imperfections in the centering of k-space [5]. The term 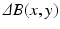 accounts for all deviations from the main magnetic field at location (x, y) which are due to both, inherent local tissue properties (which induce such local changes), as well as global object coil-loading effects. We refer here to
accounts for all deviations from the main magnetic field at location (x, y) which are due to both, inherent local tissue properties (which induce such local changes), as well as global object coil-loading effects. We refer here to 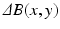 as “tissue frequency.” Finally, the noise term
as “tissue frequency.” Finally, the noise term 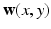 in each voxel is drawn i.i.d. from a complex Gaussian Random Variable (RV), i.e.
in each voxel is drawn i.i.d. from a complex Gaussian Random Variable (RV), i.e. 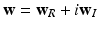 ,
, 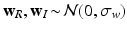 . Quantitation from MR phase requires the extraction of the term
. Quantitation from MR phase requires the extraction of the term 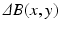 from the measurements
from the measurements 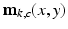 . However, instead of the absolute phase, we are restricted to measuring the numerically computed angle of
. However, instead of the absolute phase, we are restricted to measuring the numerically computed angle of 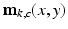 , namely,
, namely,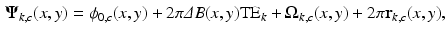
(2)
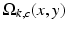 is the phase contribution of the additive noise term and
is the phase contribution of the additive noise term and 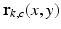 is a phase wrapping integer which forces the sum of the first three terms on the right side of (2) to be in the range
is a phase wrapping integer which forces the sum of the first three terms on the right side of (2) to be in the range 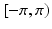 . Note that, because the noise’s contribution in the phase depends on
. Note that, because the noise’s contribution in the phase depends on 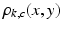 , both
, both 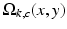 and
and 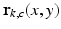 are a function of
are a function of 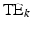 and channel c. It is clear from (2) that there are four unknowns in the angle measurements
and channel c. It is clear from (2) that there are four unknowns in the angle measurements 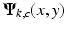 : the parameter of interest
: the parameter of interest 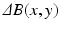 , and 3 additional sources of ambiguity (phase offset, noise and phase-wrapping integer).
, and 3 additional sources of ambiguity (phase offset, noise and phase-wrapping integer).Phase Offsets 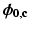 : Existing methods attempt to address this challenge by either (a) referencing
: Existing methods attempt to address this challenge by either (a) referencing 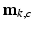 to a known coil or given location (equalization) [4, 7], (b) estimating then eliminating
to a known coil or given location (equalization) [4, 7], (b) estimating then eliminating 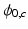 [6, 8] or (c) inverting the sensitivity profile of the coil-array [10, 12]. Equalization methods are sensitive to coil geometry, often resulting in severe artifacts in areas of low SNR, or areas of
[6, 8] or (c) inverting the sensitivity profile of the coil-array [10, 12]. Equalization methods are sensitive to coil geometry, often resulting in severe artifacts in areas of low SNR, or areas of 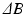 variations. Cancelation methods suffer from an inherent SNR penalty, and require separate “reference” scans which assume that
variations. Cancelation methods suffer from an inherent SNR penalty, and require separate “reference” scans which assume that 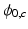 are temporally invariant [5]. Finally, inversion methods suffer from substantial errors/artifacts in areas of noise/poor regularization.
are temporally invariant [5]. Finally, inversion methods suffer from substantial errors/artifacts in areas of noise/poor regularization.
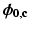 : Existing methods attempt to address this challenge by either (a) referencing
: Existing methods attempt to address this challenge by either (a) referencing 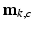 to a known coil or given location (equalization) [4, 7], (b) estimating then eliminating
to a known coil or given location (equalization) [4, 7], (b) estimating then eliminating 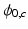 [6, 8] or (c) inverting the sensitivity profile of the coil-array [10, 12]. Equalization methods are sensitive to coil geometry, often resulting in severe artifacts in areas of low SNR, or areas of
[6, 8] or (c) inverting the sensitivity profile of the coil-array [10, 12]. Equalization methods are sensitive to coil geometry, often resulting in severe artifacts in areas of low SNR, or areas of 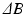 variations. Cancelation methods suffer from an inherent SNR penalty, and require separate “reference” scans which assume that
variations. Cancelation methods suffer from an inherent SNR penalty, and require separate “reference” scans which assume that 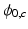 are temporally invariant [5]. Finally, inversion methods suffer from substantial errors/artifacts in areas of noise/poor regularization.
are temporally invariant [5]. Finally, inversion methods suffer from substantial errors/artifacts in areas of noise/poor regularization.Phase Noise and Wrapping: The authors in [1] have shown that imaging the MR phase signal inherently trades off two types of errors: noise and phase wrapping. There, the authors have identified three phase imaging regimes: (I) a regime dominated by phase-wrapping, with reduced levels of noise, (II) a regime dominated by noise, with no phase-wrapping and (III) a regime where the phase signal needs to be disambiguated from both phase-wrapping and noise contributions. Most phase imaging methods operate in Regime III [1] where post-processing is relied on in order to perform phase unwrapping and denoising. As carefully documented in [9], phase unwrapping methods are not robust and often require expert-user intervention. Other methods proposed in [2] use a combination of short (Regime II) and long (Regime I) echo times in order to recover the phase signal using an ML framework. However, as shown in [1], such methods are suboptimal because (a) long echo acquisitions rely on short echo acquisitions (which induces error propagation) and (b) the phase is computed using echo referencing (which induces noise amplification). Furthermore, the method in [2] relies on spatial regularization which biases the estimate.
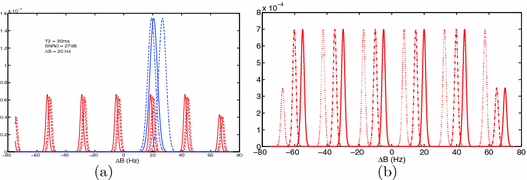

Fig. 1.
(a) Example likelihood functions, with 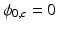 , in a voxel where
, in a voxel where 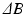 = 20 Hz, SNR0=22 (27 dB) and T2*=30 ms. The family of blue lines correspond to
= 20 Hz, SNR0=22 (27 dB) and T2*=30 ms. The family of blue lines correspond to 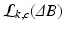 for different
for different 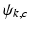 realizations, at TE = 5 ms. The red lines are
realizations, at TE = 5 ms. The red lines are 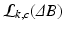 obtained at TE = 40 ms. (b)
obtained at TE = 40 ms. (b) 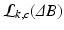 for the same voxel as (a), at TE=40 ms, but obtained through 3 channels each with different phase offsets.
for the same voxel as (a), at TE=40 ms, but obtained through 3 channels each with different phase offsets.
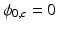 , in a voxel where
, in a voxel where 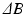 = 20 Hz, SNR0=22 (27 dB) and T2*=30 ms. The family of blue lines correspond to
= 20 Hz, SNR0=22 (27 dB) and T2*=30 ms. The family of blue lines correspond to 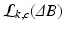 for different
for different 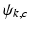 realizations, at TE = 5 ms. The red lines are
realizations, at TE = 5 ms. The red lines are 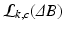 obtained at TE = 40 ms. (b)
obtained at TE = 40 ms. (b) 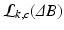 for the same voxel as (a), at TE=40 ms, but obtained through 3 channels each with different phase offsets.
for the same voxel as (a), at TE=40 ms, but obtained through 3 channels each with different phase offsets.2 MAGPI: A Maximum-Likelihood Framework
2.1 Problem Formulation
The task here is to estimate 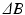 from
from 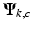 . The ML estimator is popular due to its optimality properties such as efficiency, sufficiency, consistency and invariance. We can show that the likelihood function for our problem,
. The ML estimator is popular due to its optimality properties such as efficiency, sufficiency, consistency and invariance. We can show that the likelihood function for our problem, 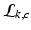 , is given by:
, is given by:
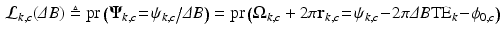
where 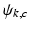 is a realization of the random variable (RV)
is a realization of the random variable (RV) 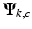 . Note that, because the phase wrapping integer
. Note that, because the phase wrapping integer 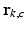 depends on the phase noise RV
depends on the phase noise RV 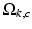 , this implies that
, this implies that 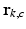 is also a (discrete) RV. Using the total probability theorem, and carrying on derivations not shown here, we can write:
is also a (discrete) RV. Using the total probability theorem, and carrying on derivations not shown here, we can write:
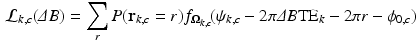
where 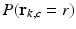 is the probability of obtaining a given wrapping integer r and
is the probability of obtaining a given wrapping integer r and 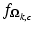 is the PDF of the noise in channel c, at echo time k, each given by:
is the PDF of the noise in channel c, at echo time k, each given by:
![$$\begin{aligned} \scriptstyle P(\mathbf{r}=r) = \frac{\sigma _{k,c} \sqrt{2}}{4\zeta _\text {max}} \left[ \frac{e^{-b_2^2} - e^{-a_2^2}}{\sqrt{\pi }} - a_2 \text {erf}(a_2) + b_2 \text {erf}(b_2) - \frac{e^{-b_1^2} - e^{-a_1^2}}{\sqrt{\pi }} + a_1 \text {erf}(a_1) - b_1 \text {erf}(b_1)\right] \end{aligned}$$](/wp-content/uploads/2016/09/A339424_1_En_4_Chapter_Equ5.gif)
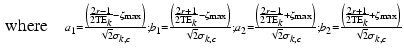
and 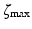 is the maximum value of
is the maximum value of 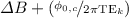 , and,
, and,
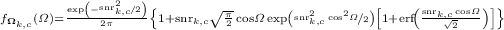
and 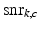 is the magnitude-domain SNR in channel c at TE
is the magnitude-domain SNR in channel c at TE . Note that our phase signal model does not assume any specific magnitude-decay model. We validated these theoretical predictions using numerical simulations and observed a close match (not shown here). We focus here on the dependence of the likelihood functions on TE
. Note that our phase signal model does not assume any specific magnitude-decay model. We validated these theoretical predictions using numerical simulations and observed a close match (not shown here). We focus here on the dependence of the likelihood functions on TE ,
, 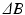 , T2* and SNR
, T2* and SNR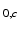 . We plot in Fig. 1(a) two families of likelihood functions obtained at two different values of TE
. We plot in Fig. 1(a) two families of likelihood functions obtained at two different values of TE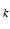 . We ignore the channel offsets (
. We ignore the channel offsets (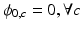 ) in this figure. We note the following: First, depending on the choice of TE
) in this figure. We note the following: First, depending on the choice of TE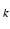 , the likelihood functions exhibit either sharp but multiple maxima (wrapping-dominated regimes), or a broad unimodal peak (noise-dominated regimes). Therefore, the likelihood function captures the inherent trade-offs between noise and phase wrapping with respect to the choice of TE
, the likelihood functions exhibit either sharp but multiple maxima (wrapping-dominated regimes), or a broad unimodal peak (noise-dominated regimes). Therefore, the likelihood function captures the inherent trade-offs between noise and phase wrapping with respect to the choice of TE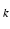 . Second, we note that repeated measurements (dashed family of lines) yield randomly shifted
. Second, we note that repeated measurements (dashed family of lines) yield randomly shifted 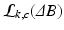 . Measurements at the larger TE
. Measurements at the larger TE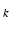 result in a family of likelihood functions that are more tightly centered around the true
result in a family of likelihood functions that are more tightly centered around the true 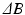 , as compared to the shorter TE
, as compared to the shorter TE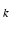 . We include the effects of the unknown phase offset in Fig. 1(b), where we plot example
. We include the effects of the unknown phase offset in Fig. 1(b), where we plot example 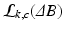 for different channels c. Note that likelihoods in the same voxel are shifted with respect to one another by an unknown amount,
for different channels c. Note that likelihoods in the same voxel are shifted with respect to one another by an unknown amount, 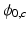 . This example illustrates that maximizing the likelihood is not trivial due to: (1) the function either having multiple maxima or one maximum whose location is sensitive to noise and (2) the unknown
. This example illustrates that maximizing the likelihood is not trivial due to: (1) the function either having multiple maxima or one maximum whose location is sensitive to noise and (2) the unknown 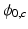 .
.
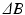 from
from 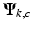 . The ML estimator is popular due to its optimality properties such as efficiency, sufficiency, consistency and invariance. We can show that the likelihood function for our problem,
. The ML estimator is popular due to its optimality properties such as efficiency, sufficiency, consistency and invariance. We can show that the likelihood function for our problem, 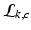 , is given by:
, is given by: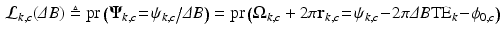
(3)
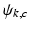 is a realization of the random variable (RV)
is a realization of the random variable (RV) 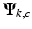 . Note that, because the phase wrapping integer
. Note that, because the phase wrapping integer 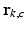 depends on the phase noise RV
depends on the phase noise RV 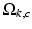 , this implies that
, this implies that 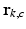 is also a (discrete) RV. Using the total probability theorem, and carrying on derivations not shown here, we can write:
is also a (discrete) RV. Using the total probability theorem, and carrying on derivations not shown here, we can write: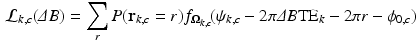
(4)
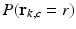 is the probability of obtaining a given wrapping integer r and
is the probability of obtaining a given wrapping integer r and 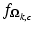 is the PDF of the noise in channel c, at echo time k, each given by:
is the PDF of the noise in channel c, at echo time k, each given by:![$$\begin{aligned} \scriptstyle P(\mathbf{r}=r) = \frac{\sigma _{k,c} \sqrt{2}}{4\zeta _\text {max}} \left[ \frac{e^{-b_2^2} - e^{-a_2^2}}{\sqrt{\pi }} - a_2 \text {erf}(a_2) + b_2 \text {erf}(b_2) - \frac{e^{-b_1^2} - e^{-a_1^2}}{\sqrt{\pi }} + a_1 \text {erf}(a_1) - b_1 \text {erf}(b_1)\right] \end{aligned}$$](/wp-content/uploads/2016/09/A339424_1_En_4_Chapter_Equ5.gif)
(5)
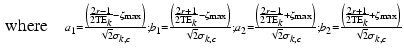
(6)
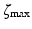 is the maximum value of
is the maximum value of 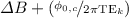 , and,
, and,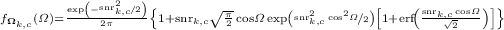
(7)
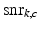 is the magnitude-domain SNR in channel c at TE
is the magnitude-domain SNR in channel c at TE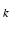 . Note that our phase signal model does not assume any specific magnitude-decay model. We validated these theoretical predictions using numerical simulations and observed a close match (not shown here). We focus here on the dependence of the likelihood functions on TE
. Note that our phase signal model does not assume any specific magnitude-decay model. We validated these theoretical predictions using numerical simulations and observed a close match (not shown here). We focus here on the dependence of the likelihood functions on TE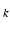 ,
, 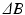 , T2* and SNR
, T2* and SNR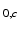 . We plot in Fig. 1(a) two families of likelihood functions obtained at two different values of TE
. We plot in Fig. 1(a) two families of likelihood functions obtained at two different values of TE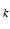 . We ignore the channel offsets (
. We ignore the channel offsets (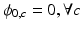 ) in this figure. We note the following: First, depending on the choice of TE
) in this figure. We note the following: First, depending on the choice of TE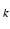 , the likelihood functions exhibit either sharp but multiple maxima (wrapping-dominated regimes), or a broad unimodal peak (noise-dominated regimes). Therefore, the likelihood function captures the inherent trade-offs between noise and phase wrapping with respect to the choice of TE
, the likelihood functions exhibit either sharp but multiple maxima (wrapping-dominated regimes), or a broad unimodal peak (noise-dominated regimes). Therefore, the likelihood function captures the inherent trade-offs between noise and phase wrapping with respect to the choice of TE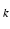 . Second, we note that repeated measurements (dashed family of lines) yield randomly shifted
. Second, we note that repeated measurements (dashed family of lines) yield randomly shifted 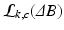 . Measurements at the larger TE
. Measurements at the larger TE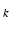 result in a family of likelihood functions that are more tightly centered around the true
result in a family of likelihood functions that are more tightly centered around the true 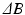 , as compared to the shorter TE
, as compared to the shorter TE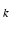 . We include the effects of the unknown phase offset in Fig. 1(b), where we plot example
. We include the effects of the unknown phase offset in Fig. 1(b), where we plot example 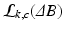 for different channels c. Note that likelihoods in the same voxel are shifted with respect to one another by an unknown amount,
for different channels c. Note that likelihoods in the same voxel are shifted with respect to one another by an unknown amount, 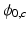 . This example illustrates that maximizing the likelihood is not trivial due to: (1) the function either having multiple maxima or one maximum whose location is sensitive to noise and (2) the unknown
. This example illustrates that maximizing the likelihood is not trivial due to: (1) the function either having multiple maxima or one maximum whose location is sensitive to noise and (2) the unknown 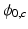 .
.
Fig. 2.
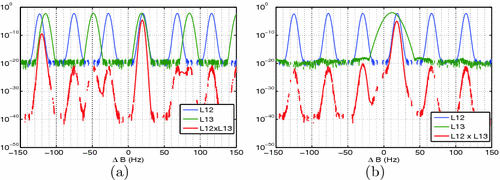
Example system likelihood functions obtained from individual dual-echo likelihoods. Note that the system likelihoods (red) are not subject to the same noise-phase wrapping trade offs as the dual-echo likelihoods (green and blue) (Color figure online).
2.2 Proposed Solution: MAGPI
Our proposed framework, coined MAGPI (Maximum AmbiGuity distance for Phase Imaging), acquires Multi-Echo Gradient Echo (MEGE) measurements from a collection of K echoes, and 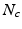 channels, within a single TR. The estimation step is described using the 3-pass process detailed below.
channels, within a single TR. The estimation step is described using the 3-pass process detailed below.
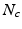 channels, within a single TR. The estimation step is described using the 3-pass process detailed below.
channels, within a single TR. The estimation step is described using the 3-pass process detailed below.Pass I: Find the most likely 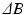 that explains the angle buildup between echoes. We can show that the angle buildup between any two echoes is:
that explains the angle buildup between echoes. We can show that the angle buildup between any two echoes is:
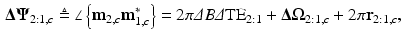
where 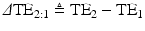 ,
, 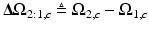 and
and 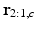 is a phase wrapping integer which forces the sum of the first two terms on the right side of (8) to be in the range
is a phase wrapping integer which forces the sum of the first two terms on the right side of (8) to be in the range 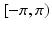 . We note two differences in (8) as compared to (2). First, the relative phase buildup does not depend on
. We note two differences in (8) as compared to (2). First, the relative phase buildup does not depend on 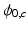 . The second important difference is a reduced tissue phase amplification (due to multiplication with a smaller term,
. The second important difference is a reduced tissue phase amplification (due to multiplication with a smaller term, 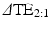 ) accompanied by noise amplification (two contributions from noise RVs). We will address this shortcoming in pass III below. The likelihood function, denoted by
) accompanied by noise amplification (two contributions from noise RVs). We will address this shortcoming in pass III below. The likelihood function, denoted by 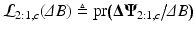 , is now given by:
, is now given by:
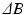 that explains the angle buildup between echoes. We can show that the angle buildup between any two echoes is:
that explains the angle buildup between echoes. We can show that the angle buildup between any two echoes is: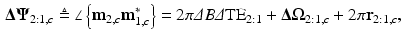
(8)
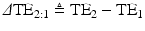 ,
, 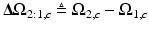 and
and 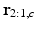 is a phase wrapping integer which forces the sum of the first two terms on the right side of (8) to be in the range
is a phase wrapping integer which forces the sum of the first two terms on the right side of (8) to be in the range 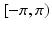 . We note two differences in (8) as compared to (2). First, the relative phase buildup does not depend on
. We note two differences in (8) as compared to (2). First, the relative phase buildup does not depend on 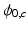 . The second important difference is a reduced tissue phase amplification (due to multiplication with a smaller term,
. The second important difference is a reduced tissue phase amplification (due to multiplication with a smaller term, 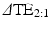 ) accompanied by noise amplification (two contributions from noise RVs). We will address this shortcoming in pass III below. The likelihood function, denoted by
) accompanied by noise amplification (two contributions from noise RVs). We will address this shortcoming in pass III below. The likelihood function, denoted by 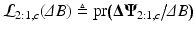 , is now given by:
, is now given by: