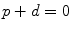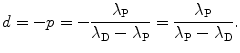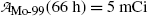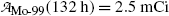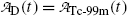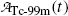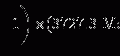(1)
Faculty of Medicine, Department, of Oncology and Medical Physics Unit, McGill University, Montreal, Québec, Canada
Abstract
Chapter 10 consists of 13 problems spread over 8 sections dealing with the kinetics of radioactivity also known as radioactive decay, nuclear transformation, and nuclear disintegration. Radioactivity is a spontaneous process by which an unstable parent nucleus emits a particle or electromagnetic radiation and transforms into a more stable daughter nucleus that may or may not be stable. An unstable nucleus will decay further in a decay series until a stable nuclear configuration is reached.
The radioactive decay is governed by the formalism based on the definition of activity and the radioactive decay constant. Henri Becquerel discovered the process of natural radioactivity in 1896 and soon thereafter in 1898 Pierre Curie and Marie Skłodowska-Curie discovered radium and polonium and coined the term “radioactivity to describe emission of “emanations” from unstable natural elements. Fréderic Joliot and Irène Joliot-Curie discovered artificial radioactivity in 1934.
The first problem of this chapter (Sect. 10.1) deals with general aspects of radioactivity, such as activity, specific activity, decay constant, half-life, mean lifetime, and units of activity. Section 10.2 contains two problems addressing the simple kinetics of radioactive parent decaying into a stable daughter. Section 10.3 is dedicated to several long problems that deal with radioactive series decay from various angles to improve the understanding of the radioactive chain decay.
Section 10.4 introduces the concept of the general form of daughter activity, while Sect. 10.5 deals with the various equilibriums in parent-daughter activities, such as secular, transient, and ideal equilibrium. Next (Sect. 10.6) come two problems on general radioactive decay series with many chain links that are handled with Bateman equations, a problem in Sect. 10.7 on decay kinetics for a mixture of two or more independently decaying radionuclides, and the chapter concludes with a problem addressing the issue of branching decay and branching fraction (Sect. 10.8).
Chapter 10 consists of 13 problems spread over 8 sections dealing with the kinetics of radioactivity also known as radioactive decay, nuclear transformation, and nuclear disintegration. Radioactivity is a spontaneous process by which an unstable parent nucleus emits a particle or electromagnetic radiation and transforms into a more stable daughter nucleus that may or may not be stable. An unstable nucleus will decay further in a decay series until a stable nuclear configuration is reached.
The radioactive decay is governed by the formalism based on the definition of activity and the radioactive decay constant. Henri Becquerel discovered the process of natural radioactivity in 1896 and soon thereafter in 1898 Pierre Curie and Marie Skłodowska-Curie discovered radium and polonium and coined the term “radioactivity to describe emission of “emanations” from unstable natural elements. Fréderic Joliot and Irène Joliot-Curie discovered artificial radioactivity in 1934.
The first problem of this chapter (Sect. 10.1) deals with general aspects of radioactivity, such as activity, specific activity, decay constant, half-life, mean lifetime, and units of activity. Section 10.2 contains two problems addressing the simple kinetics of radioactive parent decaying into a stable daughter. Section 10.3 is dedicated to several long problems that deal with radioactive series decay from various angles to improve the understanding of the radioactive chain decay.
Section 10.4 introduces the concept of the general form of daughter activity, while Sect. 10.5 deals with the various equilibriums in parent-daughter activities, such as secular, transient, and ideal equilibrium. Next (Sect. 10.6) come two problems on general radioactive decay series with many chain links that are handled with Bateman equations, a problem in Sect. 10.7 on decay kinetics for a mixture of two or more independently decaying radionuclides, and the chapter concludes with a problem addressing the issue of branching decay and branching fraction (Sect. 10.8).
10.1 General Aspects of Radioactivity
10.1.Q1 (211)
During the past century radioactivity has revolutionized science, played an important role in industrial development, introduced several new branches of physics, and helped in establishing medical physics as a branch of physics of importance to both physics and medicine.
(a)
Define radioactivity and list a few other terms that are used to describe the process.
(b)
For the following phenomena name the scientist credited with the discovery and the year of discovery: (1) Natural radioactivity, (2) Radium and polonium, (3) Exponential laws of radioactivity, (4) Artificial radioactivity, and (5) Fission.
(c)
Name and define the characteristic parameter that is used to describe a given radioactive process. Discuss the dependence of this parameter on prevailing physical conditions in radioactive atom’s environment.
(d)
In a radioactive substance that contains a large number N of identical radioactive atoms, what is the probability that a given atom will decay during a time interval Δt? Are there any restrictions on the magnitude of Δt?
(e)
Define activity 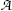 of a radioactive substance and state its relationship with the number N of radioactive atoms present in the sample. State the unit of activity in the SI system of units and in the old (traditional) system of units. Also state the relationship between the two systems.
of a radioactive substance and state its relationship with the number N of radioactive atoms present in the sample. State the unit of activity in the SI system of units and in the old (traditional) system of units. Also state the relationship between the two systems.
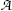 of a radioactive substance and state its relationship with the number N of radioactive atoms present in the sample. State the unit of activity in the SI system of units and in the old (traditional) system of units. Also state the relationship between the two systems.
of a radioactive substance and state its relationship with the number N of radioactive atoms present in the sample. State the unit of activity in the SI system of units and in the old (traditional) system of units. Also state the relationship between the two systems.(f)
Both hertz (Hz) and becquerel (Bq) are units of a physical quantity and equal to 1/s. What is the difference between the two units and which physical quantities do they represent?
(g)
Define specific activity a and show how it is determined for a given radionuclide. State the unit of specific activity in the SI system of units and in the old (traditional) system of units.
SOLUTION:
(a) Radioactivity is a process by which an unstable parent nucleus transforms spontaneously into one or several daughter nuclei that are more stable than the parent nucleus by having larger binding energies per nucleon than does the parent nucleus. The daughter nucleus may be stable or may also be unstable and decay further through a chain of radioactive decays until a stable nuclear configuration is reached. Radioactive decay is usually accompanied by emission of energetic particles, γ rays or both.
In addition to radioactivity, other terms used to describe spontaneous nuclear decay are radioactive decay, nuclear disintegration, nuclear transformation, and nuclear transmutation.
(b) Discoveries related to radioactivity:
(c) All radioactive decay processes are governed by the same general formalism that is based on the definition of the activity 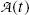 and on the total radioactive decay constant λ that is a characteristic parameter for each radioactive decay process with dimensions of reciprocal time usually in s−1. The decay constant λ is independent of the age of the radioactive atom and is essentially independent of physical conditions such as temperature, pressure, and chemical state of the atom’s environment.
and on the total radioactive decay constant λ that is a characteristic parameter for each radioactive decay process with dimensions of reciprocal time usually in s−1. The decay constant λ is independent of the age of the radioactive atom and is essentially independent of physical conditions such as temperature, pressure, and chemical state of the atom’s environment.
(1)
Natural radioactivity: Henri Becquerel (1896).
(2)
Radium and polonium: Marie Curie-Skłodowska and Pierre Curie (1898).
(3)
Exponential laws of radioactivity: Ernest Rutherford and Frederick Soddy (1902).
(4)
Artificial radioactivity: Frédéric Joliot and Irène Joliot-Curie (1934).
(5)
Fission: Lise Meitner, Otto Frisch, Otto Hahn, and Friedrich W. Strassmann (1938).
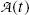 and on the total radioactive decay constant λ that is a characteristic parameter for each radioactive decay process with dimensions of reciprocal time usually in s−1. The decay constant λ is independent of the age of the radioactive atom and is essentially independent of physical conditions such as temperature, pressure, and chemical state of the atom’s environment.
and on the total radioactive decay constant λ that is a characteristic parameter for each radioactive decay process with dimensions of reciprocal time usually in s−1. The decay constant λ is independent of the age of the radioactive atom and is essentially independent of physical conditions such as temperature, pressure, and chemical state of the atom’s environment.(d) The total radioactive decay constant λ multiplied by a time interval Δt that is much smaller than 1/λ represents the probability that any particular atom of radioactive substance containing a large number N(t) of identical radioactive atoms will decay in that time interval.
(e) Activity 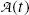 of a radioactive substance containing a large number N(t) of identical radioactive atoms represents the total number of decays per unit time and is defined as a product between N(t) and decay constant λ, i.e.,
of a radioactive substance containing a large number N(t) of identical radioactive atoms represents the total number of decays per unit time and is defined as a product between N(t) and decay constant λ, i.e.,
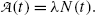
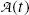 of a radioactive substance containing a large number N(t) of identical radioactive atoms represents the total number of decays per unit time and is defined as a product between N(t) and decay constant λ, i.e.,
of a radioactive substance containing a large number N(t) of identical radioactive atoms represents the total number of decays per unit time and is defined as a product between N(t) and decay constant λ, i.e.,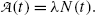
(10.1)
SI unit of activity is the becquerel (Bq) defined as 1 Bq=1 s−1. The old unit of activity, the curie (Ci), was initially defined as the activity of 1 g of radium-226 and given as 1 Ci=3.7×1010 s−1. The activity of 1 g of radium-226 was subsequently measured to be 3.665×1010 s−1; however, the definition of the curie was kept at 3.7×1010 s−1. The current value of the activity of 1 g of radium-226 is thus 0.988 Ci or 3.665×1010 Bq. The SI unit becquerel and the traditional unit curie are related as follows
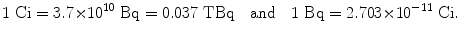
(f) Becquerel (Bq) and hertz (Hz) both correspond to 1 s−1; however, becquerel refers to physical quantity “activity” and hertz refers to periodic motion (“frequency”).
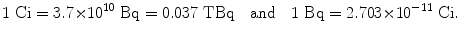
(10.2)
(g) Specific activity a of a radioactive substance is defined as the activity 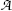 per unit mass m
per unit mass m
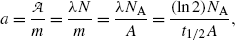
where N A is the Avogadro number (6.022×1023 mol−1), A is the atomic mass number, and t 1/2 is the half life of the radioactive substance. The units of specific activity are Bq/kg (SI unit) and Ci/g (traditional unit). The relationship between the two units is given as: 1 Ci/g=37 TBq/kg.
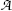 per unit mass m
per unit mass m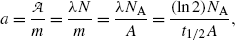
(10.3)
10.2 Decay of Radioactive Parent into a Stable Daughter
10.2.Q1 (212)
In its simplest form the radioactive decay is characterized by a radioactive parent nucleus P decaying with decay constant λ P into a stable daughter nucleus D
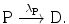
The rate of depletion of the number of radioactive parent nuclei N P(t) is equal to the activity 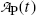 at time t, i.e.,
at time t, i.e.,
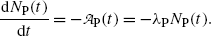
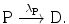
(10.4)
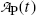 at time t, i.e.,
at time t, i.e.,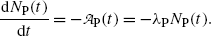
(10.5)
(a)
Solve the differential equation (10.5) to obtain the number of parent nuclei N P(t) at time t in terms of the number of parent nuclei N P(0) at time t=0.
(b)
Using the results of (a) express the activity 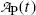 at time t in terms of the activity
at time t in terms of the activity 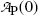 at time t=0.
at time t=0.
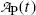 at time t in terms of the activity
at time t in terms of the activity 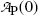 at time t=0.
at time t=0.(c)
Half-life (t 1/2)P of a radioactive substance P is defined as the time during which the number of radioactive nuclei of the substance decays to half of the initial value N P(0) present at time t=0. Show that
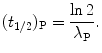
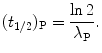
(10.6)
(d)
Obtain an expression for the average (mean) lifetime τ P of a radioactive parent substance P and derive the relationship between mean lifetime τ P and half-life (t 1/2)P.
SOLUTION:
(a) The fundamental differential equation (10.5) for describing radioactive decay can be rewritten in general integral form to get
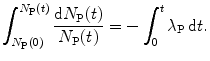
Integration of both sides of (10.7) results in the following solution
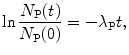
which can also be expressed as
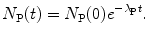
(b) The activity 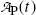 is proportional to the number of parent nuclei N P(t) and the proportionality constant is the decay constant λ P, i.e.,
is proportional to the number of parent nuclei N P(t) and the proportionality constant is the decay constant λ P, i.e.,
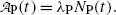
Multiplying both sides of (10.9) by the decay constant λ P and recalling (10.10) we get
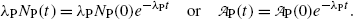
(c) The definition of half-life (t 1/2)P of a radioactive substance in conjunction with (10.9) implies the following relationship
![$$ N_{\mathrm{P}}\bigl[t = (t_{1/2})_{\mathrm{P}}\bigr] = \frac{1}{2}N_{\mathrm{P}}(0) = N_{\mathrm{P}}(0)e^{ - \lambda _{\mathrm{P}}(t_{1/2})_{\mathrm{P}}}, $$](/wp-content/uploads/2016/04/A212719_1_En_10_Chapter_Equ12.gif)
while in conjunction with (10.11) it gives the following expression
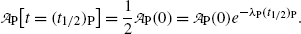
Cancelling N P(0) in (10.12) or cancelling 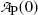 in (10.13) we first get
in (10.13) we first get
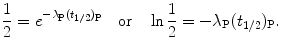
Solving (10.14) for (t 1/2)P we obtain the following relationship linking half-life (t 1/2)P of the parent nucleus with its decay constant λ P
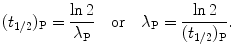
(d) The actual lifetime of any radioactive parent nucleus P can vary from 0 to ∞; however, for a large number N P of parent nuclei we can define the average (mean) lifetime or expectation value τ P of radioactive parent substance P that equals the sum of lifetimes of all individual atoms divided by the initial number N P(0) of radioactive nuclei.
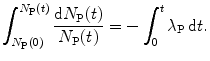
(10.7)
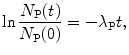
(10.8)
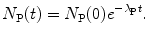
(10.9)
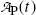 is proportional to the number of parent nuclei N P(t) and the proportionality constant is the decay constant λ P, i.e.,
is proportional to the number of parent nuclei N P(t) and the proportionality constant is the decay constant λ P, i.e.,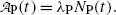
(10.10)
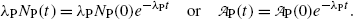
(10.11)
![$$ N_{\mathrm{P}}\bigl[t = (t_{1/2})_{\mathrm{P}}\bigr] = \frac{1}{2}N_{\mathrm{P}}(0) = N_{\mathrm{P}}(0)e^{ - \lambda _{\mathrm{P}}(t_{1/2})_{\mathrm{P}}}, $$](/wp-content/uploads/2016/04/A212719_1_En_10_Chapter_Equ12.gif)
(10.12)
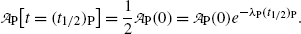
(10.13)
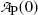 in (10.13) we first get
in (10.13) we first get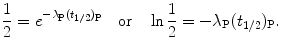
(10.14)
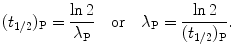
(10.15)
The average (mean) lifetime τ P thus represents the average life expectancy of all nuclei in radioactive substance P at time t=0; i.e.,
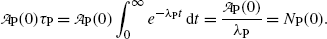
Therefore, mean lifetime τ P, half-life (t 1/2)P, and the decay constant λ P are related through the following expression
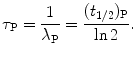
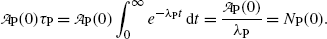
(10.16)
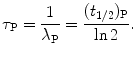
(10.17)
Inserting (10.17) into (10.9), the mean life τ P can also be defined as the time required for the number of radioactive atoms N P(t) to fall from its initial value N P(0) at time t=0 to a value of e −1 N P(0) corresponding to 0.368N P(0) or to 36.8 % of N P(0) at time t=τ P. In similar fashion, inserting (10.17) into (10.11), the mean life τ P can be defined as the time required for the activity of radioactive substance 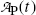 to fall from its initial value
to fall from its initial value 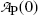 at time t=0 to a value of
at time t=0 to a value of 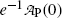 corresponding to
corresponding to 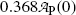 or to 36.8 % of
or to 36.8 % of 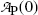 at time t=τ P.
at time t=τ P.
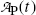 to fall from its initial value
to fall from its initial value 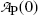 at time t=0 to a value of
at time t=0 to a value of 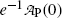 corresponding to
corresponding to 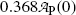 or to 36.8 % of
or to 36.8 % of 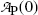 at time t=τ P.
at time t=τ P.The mean (average) survival life τ P of a parent nucleus P can also be determined using the standard method for finding the average (mean) of a continuous variable as follows
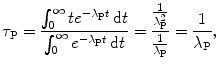
where the integral in the numerator of (10.18) is determined using the method of integration by parts.
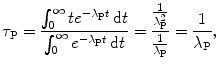
(10.18)
10.2.Q2 (213)
Data in Table 10.1 represent measured activity 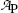 in millicuries (mCi) as a function of time t for an unknown radionuclide P that decays into a stable daughter D. For the unknown radionuclide substance P:
in millicuries (mCi) as a function of time t for an unknown radionuclide P that decays into a stable daughter D. For the unknown radionuclide substance P:
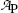 in millicuries (mCi) as a function of time t for an unknown radionuclide P that decays into a stable daughter D. For the unknown radionuclide substance P:
in millicuries (mCi) as a function of time t for an unknown radionuclide P that decays into a stable daughter D. For the unknown radionuclide substance P:(a)
Plot the data of Table 10.1 in the format of activity 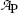 against time t on Cartesian and semi-logarithmic graph paper and estimate the decay half-life (t 1/2)P of radionuclide P.
against time t on Cartesian and semi-logarithmic graph paper and estimate the decay half-life (t 1/2)P of radionuclide P.
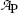 against time t on Cartesian and semi-logarithmic graph paper and estimate the decay half-life (t 1/2)P of radionuclide P.
against time t on Cartesian and semi-logarithmic graph paper and estimate the decay half-life (t 1/2)P of radionuclide P.(b)
Using the least squares fit to measured data determine the decay constant λ P.
(c)
Determine the half-life (t 1/2)P.
(d)
Determine the mean lifetime τ P.
Table 10.1
Measured activity 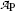 measured at various times t after the first measurement
measured at various times t after the first measurement 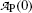 at time t=0 for radioactive parent P decaying into stable daughter D
at time t=0 for radioactive parent P decaying into stable daughter D
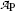 measured at various times t after the first measurement
measured at various times t after the first measurement 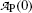 at time t=0 for radioactive parent P decaying into stable daughter D
at time t=0 for radioactive parent P decaying into stable daughter DTime t (min) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 8 | 10 | 12 |
Activity 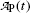 (mCi) (mCi) | 3.6 | 3.2 | 2.8 | 2.4 | 2.1 | 1.9 | 1.6 | 1.3 | 1.0 | 0.7 |
SOLUTION:
(a) Measured data presented in Table 10.1 are depicted in Fig. 10.1 with activity 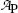 plotted on the ordinate (y axis) and time t on the abscissa (x axis). Part (A) is plotted on Cartesian scale, part (B) on semi-logarithmic (log-lin) scale. Both graphs support the assumption that the relationship between activity
plotted on the ordinate (y axis) and time t on the abscissa (x axis). Part (A) is plotted on Cartesian scale, part (B) on semi-logarithmic (log-lin) scale. Both graphs support the assumption that the relationship between activity 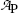 and time t is exponential.
and time t is exponential.
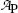 plotted on the ordinate (y axis) and time t on the abscissa (x axis). Part (A) is plotted on Cartesian scale, part (B) on semi-logarithmic (log-lin) scale. Both graphs support the assumption that the relationship between activity
plotted on the ordinate (y axis) and time t on the abscissa (x axis). Part (A) is plotted on Cartesian scale, part (B) on semi-logarithmic (log-lin) scale. Both graphs support the assumption that the relationship between activity 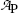 and time t is exponential.
and time t is exponential.
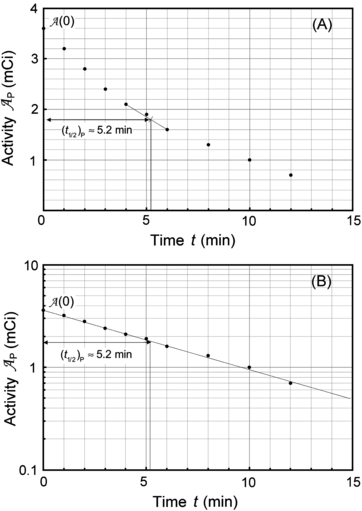
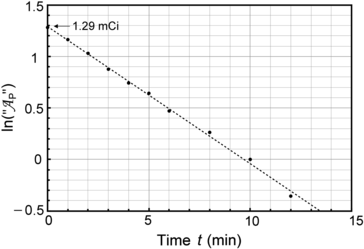
Fig. 10.1
Data of Table 10.1 for activity of parent P decaying into daughter D plotted in (A) on Cartesian scale and in (B) on semi-logarithmic scale. Rough estimate of half-life (t 1/2)P=5.2 min is 5.2 minutes
Activity 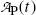 at time t of parent nuclide P decaying into stable daughter D is described by the following exponential expression
at time t of parent nuclide P decaying into stable daughter D is described by the following exponential expression
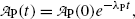
where 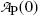 is the parent activity at time t=0 and λ P is a decay parameter referred to as the decay constant related to half-life (t 1/2)P and mean lifetime τ P as follows
is the parent activity at time t=0 and λ P is a decay parameter referred to as the decay constant related to half-life (t 1/2)P and mean lifetime τ P as follows
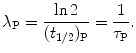
Based on graphs in Fig. 10.1 we can estimate the half-life (t 1/2)P of the unknown radioactive substance P by estimating the time required for the activity 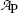 to decrease from
to decrease from 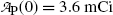 to
to 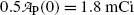 . This direct approach results in an estimate of (t 1/2)P≈5.2 min.
. This direct approach results in an estimate of (t 1/2)P≈5.2 min.
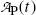 at time t of parent nuclide P decaying into stable daughter D is described by the following exponential expression
at time t of parent nuclide P decaying into stable daughter D is described by the following exponential expression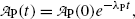
(10.19)
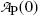 is the parent activity at time t=0 and λ P is a decay parameter referred to as the decay constant related to half-life (t 1/2)P and mean lifetime τ P as follows
is the parent activity at time t=0 and λ P is a decay parameter referred to as the decay constant related to half-life (t 1/2)P and mean lifetime τ P as follows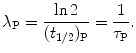
(10.20)
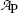 to decrease from
to decrease from 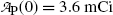 to
to 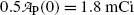 . This direct approach results in an estimate of (t 1/2)P≈5.2 min.
. This direct approach results in an estimate of (t 1/2)P≈5.2 min.(b) To improve on the rough estimate of (t 1/2)P≈5.2 min in (a) we now apply the method of linear curve fitting based on least-squares fit to measured data. To determine the decay constant λ P from the data presented in Table 10.1 we first transform (10.19) into a linear function by applying the natural algorithm to both sides of (10.19) as follows
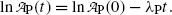
Equation (10.21) is a linear equation of the standard form y=b+ax with dependent variable y given as 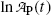 , ordinate (y) axis intercept b given as
, ordinate (y) axis intercept b given as 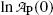 , dependent variable x given as t, and slope a given as −λ P. We assume that values of the independent variable x i are set accurately and values of the dependent variable y i are measurements subject to some small uncertainty.
, dependent variable x given as t, and slope a given as −λ P. We assume that values of the independent variable x i are set accurately and values of the dependent variable y i are measurements subject to some small uncertainty.
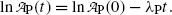
(10.21)
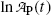 , ordinate (y) axis intercept b given as
, ordinate (y) axis intercept b given as 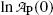 , dependent variable x given as t, and slope a given as −λ P. We assume that values of the independent variable x i are set accurately and values of the dependent variable y i are measurements subject to some small uncertainty.
, dependent variable x given as t, and slope a given as −λ P. We assume that values of the independent variable x i are set accurately and values of the dependent variable y i are measurements subject to some small uncertainty.Next we apply the method of least squares fit using the following standard least squares fit expressions for the slope a of the linear function (10.21) and the y intercept b of the linear function
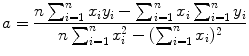
and
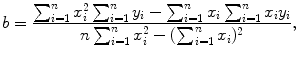
where i is the running index and n is the number of data points in a particular set of data. In Table 10.2 we show the individual components (x i , y i , 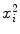 , and x i y i ) of the data set used for the least squares fit method. In addition, row (12) of the table gives the calculated sums
, and x i y i ) of the data set used for the least squares fit method. In addition, row (12) of the table gives the calculated sums 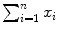 ,
, 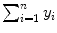 ,
, 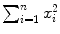 , and
, and 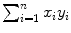 for use in (10.22) and (10.23) in determination of a and b.
for use in (10.22) and (10.23) in determination of a and b.
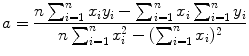
(10.22)
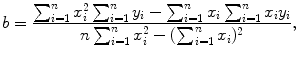
(10.23)
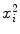 , and x i y i ) of the data set used for the least squares fit method. In addition, row (12) of the table gives the calculated sums
, and x i y i ) of the data set used for the least squares fit method. In addition, row (12) of the table gives the calculated sums 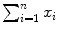 ,
, 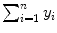 ,
, 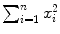 , and
, and 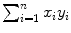 for use in (10.22) and (10.23) in determination of a and b.
for use in (10.22) and (10.23) in determination of a and b.Table 10.2
Parameters x i , y i , 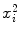 , and x i y i for the data set presented in Table 10.1 representing measured activity
, and x i y i for the data set presented in Table 10.1 representing measured activity 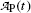 as a function of time t for a radioactive parent nucleus P decaying into a stable daughter D. Row (12) of the table provides the sum of the individual components for parameters x i , y i ,
as a function of time t for a radioactive parent nucleus P decaying into a stable daughter D. Row (12) of the table provides the sum of the individual components for parameters x i , y i , 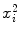 , and x i y i
, and x i y i
 , and x i y i for the data set presented in Table 10.1 representing measured activity
, and x i y i for the data set presented in Table 10.1 representing measured activity 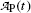 as a function of time t for a radioactive parent nucleus P decaying into a stable daughter D. Row (12) of the table provides the sum of the individual components for parameters x i , y i ,
as a function of time t for a radioactive parent nucleus P decaying into a stable daughter D. Row (12) of the table provides the sum of the individual components for parameters x i , y i , 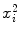 , and x i y i
, and x i y i (1) | i | x i | y i | 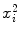 | x i y i |
|---|---|---|---|---|---|
(2) | 1 | 0 | 1.281 | 0 | 0.000 |
(3) | 2 | 1 | 1.163 | 1 | 1.163 |
(4) | 3 | 2 | 1.030 | 4 | 2.059 |
(5) | 4 | 3 | 0.875 | 9 | 2.626 |
(6) | 5 | 4 | 0.742 | 16 | 2.968 |
(7) | 6 | 5 | 0.642 | 25 | 3.209 |
(8) | 7 | 6 | 0.470 | 36 | 2.820 |
(9) | 8 | 8 | 0.262 | 64 | 2.099 |
(10) | 9 | 10 | 0.000 | 100 | 0 |
(11) | 10 | 12 | −0.357 | 144 | −4.280 |
(12) | SUM 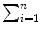 | 51 | 6.109 | 399 | 12.665 |
Data in row (12) of Table 10.2 in conjunction with (10.22) and (10.23) give the following results for the slope a and y intercept b, respectively,
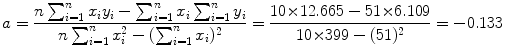
and
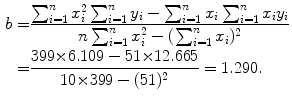
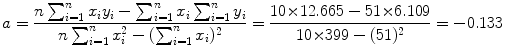
(10.24)
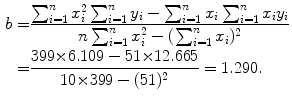
(10.25)
A plot of the data points (x i ,y i ) from Table 10.2 as well as the line y=b+ax with slope a=−0.133 and y intercept b=1.29 is shown in Fig. 10.2. From (10.24) and (10.25) we can now determine the decay constant λ P and the initial activity 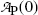 as follows
as follows
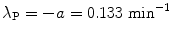
and
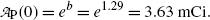
(c) Half-life (t 1/2)P of the radionuclide P is determined from the well-known relationship between (t 1/2)P and λ P given in (10.20) as
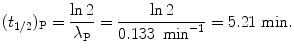
Mean lifetime τ P of the radionuclide P is also determined from (10.20)
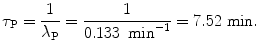
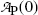 as follows
as follows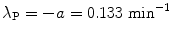
(10.26)
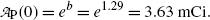
(10.27)
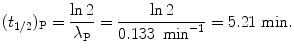
(10.28)
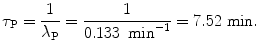
(10.29)

Fig. 10.2
Plot of the data points (x i ,y i ) from Table 10.2 as well as the line y=b+ax with slope a=−0.133 and y intercept b=1.29
10.3 Radioactive Series Decay
10.3.Q1 (214)
Radioactive decay through a series of radioactive transformations is much more common than the simple radioactive decay from a radioactive parent into stable daughter. The radioactive decay series forms a decay chain starting with the parent radionuclide and moves through several generations to eventually end with a stable nuclide.
Consider the simple chain P→D→G where both the parent P and daughter D are radioactive and the granddaughter G is stable. The parent decays with a decay constant λ P while the daughter decays with a decay constant λ D. For this simple decay series:
(a)
State the differential equations governing the kinetics of the radioactive parent and radioactive daughter.
(b)
Solve the differential equations in (a) with the following initial conditions:
to get expressions for the number of parent nuclei N P and for the number of daughter nuclei N D(t) as a function of time t.
(1)
Initial number of parent nuclei N P(t) at time t=0 is N P(0).
(2)
Initial number of daughter nuclei N D(t=0)=N D(0)=0.
(c)
Using the results of (b) obtain an expression for activity of the daughter 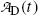 .
.
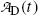 .
.(d)
The expression for the daughter activity 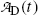 derived in (c) should predict
derived in (c) should predict 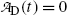 for t=0 [recall the initial condition N D(0)=0] as well as for t→∞ (recall that at t=∞ all daughter nuclei will have decayed). This means that
for t=0 [recall the initial condition N D(0)=0] as well as for t→∞ (recall that at t=∞ all daughter nuclei will have decayed). This means that 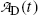 must reach a maximum value
must reach a maximum value 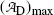 at a characteristic time (t max)D somewhere between the two extremes: t=0 and t=∞, i.e., 0<(t max)D<∞. Derive an expression for the characteristic time (t max)D.
at a characteristic time (t max)D somewhere between the two extremes: t=0 and t=∞, i.e., 0<(t max)D<∞. Derive an expression for the characteristic time (t max)D.
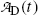 derived in (c) should predict
derived in (c) should predict 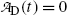 for t=0 [recall the initial condition N D(0)=0] as well as for t→∞ (recall that at t=∞ all daughter nuclei will have decayed). This means that
for t=0 [recall the initial condition N D(0)=0] as well as for t→∞ (recall that at t=∞ all daughter nuclei will have decayed). This means that 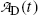 must reach a maximum value
must reach a maximum value 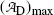 at a characteristic time (t max)D somewhere between the two extremes: t=0 and t=∞, i.e., 0<(t max)D<∞. Derive an expression for the characteristic time (t max)D.
at a characteristic time (t max)D somewhere between the two extremes: t=0 and t=∞, i.e., 0<(t max)D<∞. Derive an expression for the characteristic time (t max)D.(e)
Show that for λ P≳λ D (but not λ P=λ D) and for λ P≲λ D (but not λ P=λ D) the characteristic time (t max)D can be approximated by 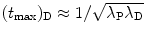 . To verify this approximation calculate (t max)D with this approximation and compare results with the expression derived in (d) for the following two radioactive series decays: (1) Series decay with λ P=2.1 y−1 and λ D=2.0 y−1 and (2) Series decay with λ P=5.1 s−1 and λ P=5.5 s−1.
. To verify this approximation calculate (t max)D with this approximation and compare results with the expression derived in (d) for the following two radioactive series decays: (1) Series decay with λ P=2.1 y−1 and λ D=2.0 y−1 and (2) Series decay with λ P=5.1 s−1 and λ P=5.5 s−1.
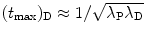 . To verify this approximation calculate (t max)D with this approximation and compare results with the expression derived in (d) for the following two radioactive series decays: (1) Series decay with λ P=2.1 y−1 and λ D=2.0 y−1 and (2) Series decay with λ P=5.1 s−1 and λ P=5.5 s−1.
. To verify this approximation calculate (t max)D with this approximation and compare results with the expression derived in (d) for the following two radioactive series decays: (1) Series decay with λ P=2.1 y−1 and λ D=2.0 y−1 and (2) Series decay with λ P=5.1 s−1 and λ P=5.5 s−1.SOLUTION:
(a) The differential equations governing the kinetics of the parent P and the daughter D nuclei in the simple P→D→G decay chain describe the rate of change in the number of parent nuclei N P(t) and in the number of daughter nuclei N D(t).
(b) Equation (10.30) shows that the parent P follows a straightforward radioactive decay process with the initial condition N P(t=0)=N P(0) and the following solution
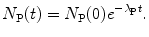
The solution to (10.31) for the daughter, on the other hand, is more complicated and will be determined after inserting (10.32) into (10.31) to get the following expression for the rate of change in the number of daughter nuclei
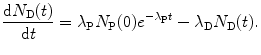
The general solution of the differential equation given by (10.33) is given as
![$$ N_{\mathrm{D}}(t) = N_{\mathrm{P}}(0) \bigl[pe^{ - \lambda _{\mathrm{P}}t} + de^{ - \lambda _{\mathrm{D}}t}\bigr], $$](/wp-content/uploads/2016/04/A212719_1_En_10_Chapter_Equ34.gif)
where p and d are constants to be determined using the following four steps:
After inserting (10.37) and (10.39) into (10.34) we get the following expression for the number of daughter nuclei N D(t) as a function of time t
![$$ N_{\mathrm{D}}(t) = N_{\mathrm{P}}(0)\frac{\lambda _{\mathrm{P}}}{\lambda _{\mathrm{D}} - \lambda _{\mathrm{P}}} \bigl[e^{ - \lambda _{\mathrm{P}}t} - e^{ - \lambda _{\mathrm{D}}t}\bigr]. $$](/wp-content/uploads/2016/04/A212719_1_En_10_Chapter_Equ40.gif)
(c) The simple P→D→G radioactive series decay with radioactive parent P decaying through radioactive daughter D into stable grand-daughter G is characterized by equations describing the number of parent nuclei N P(t) and number of daughter nuclei N D(t) given by (10.32) and (10.40), respectively. Activities 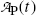 and
and 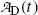 of the parent and daughter, respectively, in a radioactive sample are also of interest and can be determined by recalling that, in general, the activity
of the parent and daughter, respectively, in a radioactive sample are also of interest and can be determined by recalling that, in general, the activity 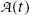 of a radionuclide is the product of its decay constant λ and the number N(t) of radioactive nuclei present in the sample.
of a radionuclide is the product of its decay constant λ and the number N(t) of radioactive nuclei present in the sample.
(1)
For the parent, the rate of change dN P(t)/dt in the number of parent nuclei is given by the standard expression dealing with nuclear decay
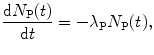
with the minus sign indicating a decrease in the number of parent nuclei N P(t) with increasing time t.
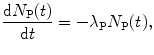
(10.30)
(2)
The rate of change dN D(t)/dt in the number of daughter nuclei D is equal to the supply of new daughter nuclei D through the decay of P given as λ P N P(t) and the loss of daughter nuclei D from the decay of D to G given as [−λ D N D(t)]. The rate of change dN D/dt is expressed as


(10.31)
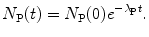
(10.32)
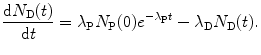
(10.33)
![$$ N_{\mathrm{D}}(t) = N_{\mathrm{P}}(0) \bigl[pe^{ - \lambda _{\mathrm{P}}t} + de^{ - \lambda _{\mathrm{D}}t}\bigr], $$](/wp-content/uploads/2016/04/A212719_1_En_10_Chapter_Equ34.gif)
(10.34)
3.
The factor in square brackets of (10.36) must be equal to zero to satisfy the equation for all possible values of t, yielding the following expression for the constant p
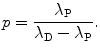
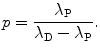
(10.37)
![$$ N_{\mathrm{D}}(t) = N_{\mathrm{P}}(0)\frac{\lambda _{\mathrm{P}}}{\lambda _{\mathrm{D}} - \lambda _{\mathrm{P}}} \bigl[e^{ - \lambda _{\mathrm{P}}t} - e^{ - \lambda _{\mathrm{D}}t}\bigr]. $$](/wp-content/uploads/2016/04/A212719_1_En_10_Chapter_Equ40.gif)
(10.40)
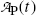 and
and 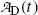 of the parent and daughter, respectively, in a radioactive sample are also of interest and can be determined by recalling that, in general, the activity
of the parent and daughter, respectively, in a radioactive sample are also of interest and can be determined by recalling that, in general, the activity 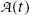 of a radionuclide is the product of its decay constant λ and the number N(t) of radioactive nuclei present in the sample.
of a radionuclide is the product of its decay constant λ and the number N(t) of radioactive nuclei present in the sample.We thus get the following expressions for the activity of the parent 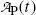 from (10.32) and activity of the daughter
from (10.32) and activity of the daughter 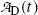 from (10.40), respectively
from (10.40), respectively
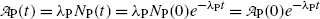
and
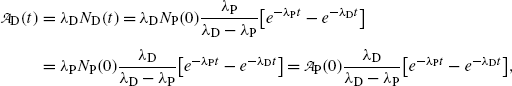
where 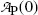 is the activity of the parent at time t=0.
is the activity of the parent at time t=0.
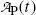 from (10.32) and activity of the daughter
from (10.32) and activity of the daughter 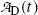 from (10.40), respectively
from (10.40), respectively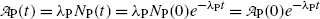
(10.41)
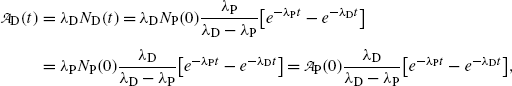
(10.42)
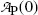 is the activity of the parent at time t=0.
is the activity of the parent at time t=0.A test of the limiting value of 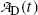 given in (10.42) for t=0 and t→∞ yields zero, as it should according to: (1) initial condition N D(0)=0 and (2) at t=∞ all daughter nuclei will have decayed. From (10.42) we note: (1)
given in (10.42) for t=0 and t→∞ yields zero, as it should according to: (1) initial condition N D(0)=0 and (2) at t=∞ all daughter nuclei will have decayed. From (10.42) we note: (1) 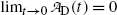 and (2)
and (2) 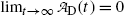 .
.
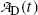 given in (10.42) for t=0 and t→∞ yields zero, as it should according to: (1) initial condition N D(0)=0 and (2) at t=∞ all daughter nuclei will have decayed. From (10.42) we note: (1)
given in (10.42) for t=0 and t→∞ yields zero, as it should according to: (1) initial condition N D(0)=0 and (2) at t=∞ all daughter nuclei will have decayed. From (10.42) we note: (1) 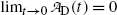 and (2)
and (2) 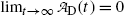 .
.(d) The characteristic time (t max)D at which the daughter activity 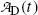 attains its maximum value
attains its maximum value 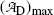 is determined by setting
is determined by setting 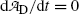 at t=(t max)D and solving for (t max)D to get
at t=(t max)D and solving for (t max)D to get
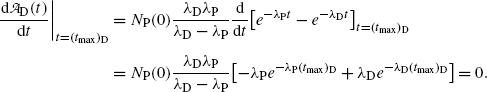
From (10.43) we first get
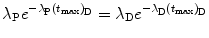
then
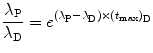
and finally get the following general result for (t max)D
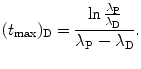
(e) For λ P≳λ D and 0<ε≪1 we assume the following relationship between decay constants λ P and λ D of the parent and daughter, respectively
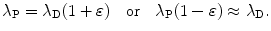
Inserting (10.47) into (10.46) we get
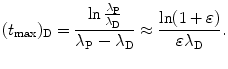
The logarithm in (10.48) can be simplified with Taylor expansion into a series as follows
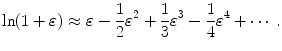
For very small ε we insert (10.47) and the first two terms of the Taylor series (10.49) into (10.48) and get the following expression for (t max)D
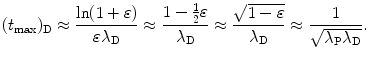
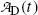 attains its maximum value
attains its maximum value 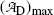 is determined by setting
is determined by setting 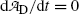 at t=(t max)D and solving for (t max)D to get
at t=(t max)D and solving for (t max)D to get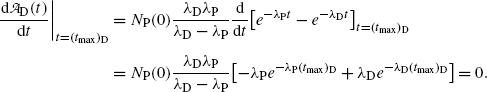
(10.43)
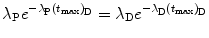
(10.44)
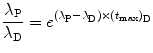
(10.45)
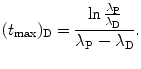
(10.46)
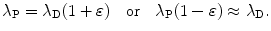
(10.47)
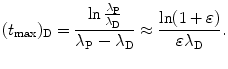
(10.48)
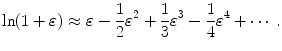
(10.49)
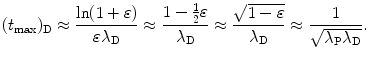
(10.50)
Similarly, for λ P λ D and 0<ε≪1 we assume the following relationship
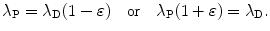
Inserting (10.51) into (10.48) we get
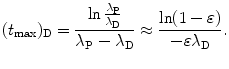
The logarithm in (10.52) can be simplified with Taylor expansion into a series as follows
![$$ \ln (1 - \varepsilon ) \approx - \biggl[\varepsilon + \frac{1}{2} \varepsilon ^{2} + \frac{1}{3}\varepsilon ^{3} + \frac{1}{4}\varepsilon ^{4} +\cdots\biggr]. $$](/wp-content/uploads/2016/04/A212719_1_En_10_Chapter_Equ53.gif)
For very small ε we insert (10.51) and the first two terms of the Taylor expansion (10.53) into (10.52) and get the following expression for (t max)D
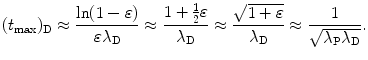
We now compare results of (t max)D calculation with the general expression for (t max)D given in (10.46) and with the approximation given in (10.51) and (10.54).
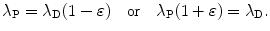
(10.51)
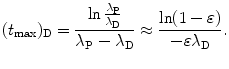
(10.52)
![$$ \ln (1 - \varepsilon ) \approx - \biggl[\varepsilon + \frac{1}{2} \varepsilon ^{2} + \frac{1}{3}\varepsilon ^{3} + \frac{1}{4}\varepsilon ^{4} +\cdots\biggr]. $$](/wp-content/uploads/2016/04/A212719_1_En_10_Chapter_Equ53.gif)
(10.53)
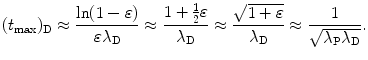
(10.54)
(1) Series decay with λ P=2.1 y−1 and λ D=2.0 y−1 for which λ P λ D
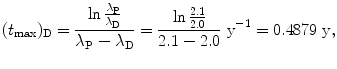
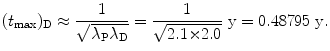
(2) Series decay with λ P=5.1 s−1 and λ P=5.5 s−1
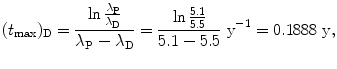
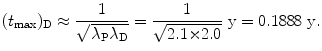
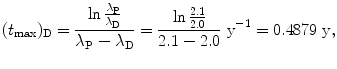
(10.55)
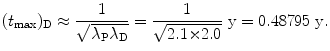
(10.56)
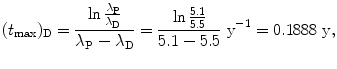
(10.57)
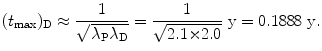
(10.58)
10.3.Q2 (215)
The molybdenum-99 (Mo-99) → technetium-99m (Tc-99m) → technetium-99 (Tc-99) decay series plays an important role in nuclear medicine, since it serves as the source of Tc-99m, the most widely used radionuclide for nuclear imaging tests. The series parent radionuclide Mo-99 decays through β − decay with a half-life (t 1/2)Mo-99=66.0 hours into daughter radionuclide Tc-99m. Subsequently, the daughter Tc-99m decays through gamma emission with a half-life (t 1/2)Tc-99m=6.02 hours to the granddaughter radionuclide Tc-99. The Tc-99 radionuclide has a much longer half-life [(t 1/2)Tc-99=2.1×105 y] in comparison with Mo-99 and Tc-99m and decays through β − decay to ruthenium-99 (Ru-99).
Starting with a pure 10 mCi (0.37 GBq) Mo-99 source:
(a)
State or derive equations for activities of the Mo-99 parent and Tc-99m daughter as a function of time.
(b)
Calculate the characteristic time (t max)Tc-99m at which the Tc-99m daughter radionuclide attains its maximum activity.
(c)
Determine the maximum activity 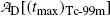 of the Tc-99m radionuclide.
of the Tc-99m radionuclide.
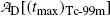 of the Tc-99m radionuclide.
of the Tc-99m radionuclide.(d)
Show that activities of the parent 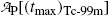 and the daughter
and the daughter 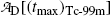 are equal at the characteristic time (t max)Tc-99m.
are equal at the characteristic time (t max)Tc-99m.
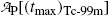 and the daughter
and the daughter 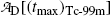 are equal at the characteristic time (t max)Tc-99m.
are equal at the characteristic time (t max)Tc-99m.(e)
Sketch the activities of the Mo-99 parent and Tc-99m daughter as a function of time and highlight the salient features of the two radioactive decay curves.
SOLUTION:
(a) Activities of the parent 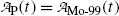 and of the daughter
and of the daughter 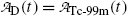 as a function of time t are, respectively, given by [see (T10.10) and (T10.35), respectively]
as a function of time t are, respectively, given by [see (T10.10) and (T10.35), respectively]
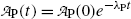
or
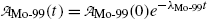
and
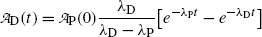
or
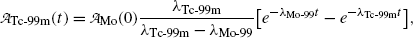
where
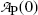
Decay constants λ for molybdenum-99 and technetium-99m are obtained from their known half-lives t 1/2 using the standard relationship λ=(ln2)/t 1/2. Thus, for Mo-99 we have
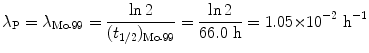
and for Tc-99m
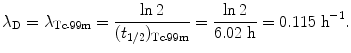
Inserting (10.63) and (10.64) into (10.59) and (10.61) and using the initial activity 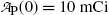 of the parent (Mo-99) radionuclide we get
of the parent (Mo-99) radionuclide we get
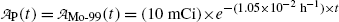
and
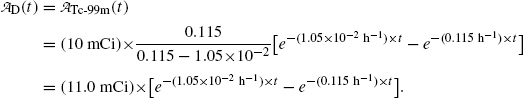
(b) Activity of the parent 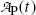 falls exponentially with increasing time t; however, activity of the daughter
falls exponentially with increasing time t; however, activity of the daughter 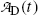 initially increases from zero to reach a maximum at a specific characteristic time (t max)D and then decreases with increasing time t to return to zero at t→∞.
initially increases from zero to reach a maximum at a specific characteristic time (t max)D and then decreases with increasing time t to return to zero at t→∞.
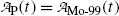 and of the daughter
and of the daughter 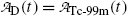 as a function of time t are, respectively, given by [see (T10.10) and (T10.35), respectively]
as a function of time t are, respectively, given by [see (T10.10) and (T10.35), respectively]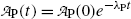
(10.59)
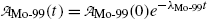
(10.60)
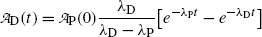
(10.61)
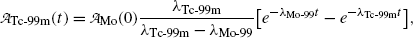
(10.62)
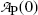
is the activity of the parent P at time t=0.
λ P
is the decay constant for the parent P radionuclide.
λ D
is the decay constant for the daughter D radionuclide.
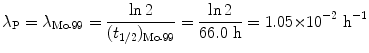
(10.63)
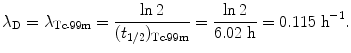
(10.64)
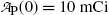 of the parent (Mo-99) radionuclide we get
of the parent (Mo-99) radionuclide we get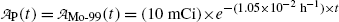
(10.65)
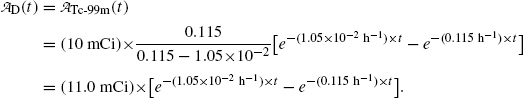
(10.66)
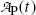 falls exponentially with increasing time t; however, activity of the daughter
falls exponentially with increasing time t; however, activity of the daughter 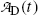 initially increases from zero to reach a maximum at a specific characteristic time (t max)D and then decreases with increasing time t to return to zero at t→∞.
initially increases from zero to reach a maximum at a specific characteristic time (t max)D and then decreases with increasing time t to return to zero at t→∞.The characteristic time (t max)D is determined by setting 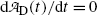 at t=(t max)D. Differentiating (10.61) results in
at t=(t max)D. Differentiating (10.61) results in
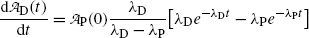
and setting 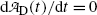 at t=(t max)D we get
at t=(t max)D we get
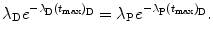
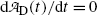 at t=(t max)D. Differentiating (10.61) results in
at t=(t max)D. Differentiating (10.61) results in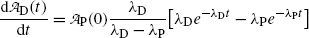
(10.67)
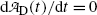 at t=(t max)D we get
at t=(t max)D we get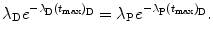
(10.68)
Solving (10.68) for (t max)D finally yields the following result for characteristic time (t max)D
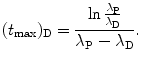
For the Mo-99 → Tc-99m → Tc-99 decay series the characteristic time (t max)D at which 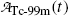 attains its maximum value is calculated as follows
attains its maximum value is calculated as follows
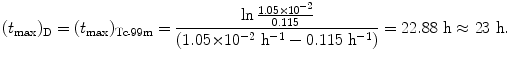
(c) Maximum activity 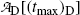 of the daughter Tc-99m at (t max)D is obtained by inserting into (10.66) the characteristic time t=(t max)D≈22.88 hr that was calculated in (10.70) to get
of the daughter Tc-99m at (t max)D is obtained by inserting into (10.66) the characteristic time t=(t max)D≈22.88 hr that was calculated in (10.70) to get
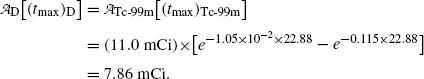
(d) Daughter activity 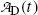 in (10.61) can be expressed as a function of parent activity
in (10.61) can be expressed as a function of parent activity 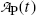 as follows
as follows
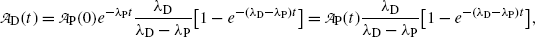
and at characteristic time (t max)D (10.72) becomes
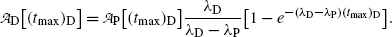
Inserting (10.69) for (t max)D into (10.73) gives the following expression for 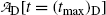
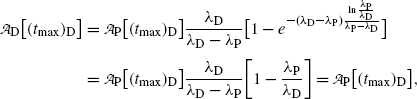
showing explicitly that at t=(t max)D the parent and daughter activities are equal.
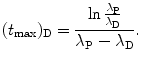
(10.69)
 attains its maximum value is calculated as follows
attains its maximum value is calculated as follows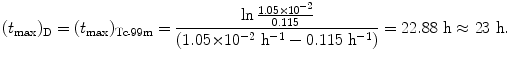
(10.70)
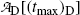 of the daughter Tc-99m at (t max)D is obtained by inserting into (10.66) the characteristic time t=(t max)D≈22.88 hr that was calculated in (10.70) to get
of the daughter Tc-99m at (t max)D is obtained by inserting into (10.66) the characteristic time t=(t max)D≈22.88 hr that was calculated in (10.70) to get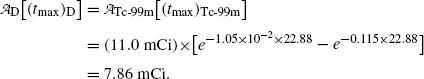
(10.71)
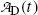 in (10.61) can be expressed as a function of parent activity
in (10.61) can be expressed as a function of parent activity 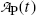 as follows
as follows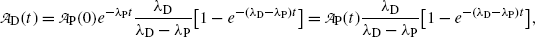
(10.72)
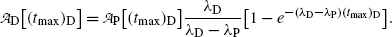
(10.73)
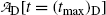
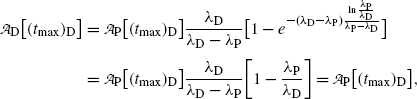
(10.74)
We now determine the maximum activity of the daughter Tc-99m in  using (10.65) with t=(t max)D≈22.88 hr
using (10.65) with t=(t max)D≈22.88 hr
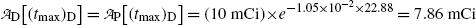
and obtain the same result as we did with (10.66) for the daughter activity  . Thus, at t=(t max)D activities of the parent and the daughter are equal in general and, in our case with 10 mCi parent at t=0, the activity of parent and daughter are 7.86 mCi and (t max)D≈23 h.
. Thus, at t=(t max)D activities of the parent and the daughter are equal in general and, in our case with 10 mCi parent at t=0, the activity of parent and daughter are 7.86 mCi and (t max)D≈23 h.
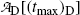 using (10.65) with t=(t max)D≈22.88 hr
using (10.65) with t=(t max)D≈22.88 hr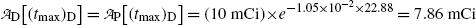
(10.75)
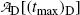 . Thus, at t=(t max)D activities of the parent and the daughter are equal in general and, in our case with 10 mCi parent at t=0, the activity of parent and daughter are 7.86 mCi and (t max)D≈23 h.
. Thus, at t=(t max)D activities of the parent and the daughter are equal in general and, in our case with 10 mCi parent at t=0, the activity of parent and daughter are 7.86 mCi and (t max)D≈23 h.(e) The parent (Mo-99) and daughter (Tc-99m) activities 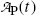 and
and 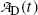 , respectively, are shown in Fig. 10.3 plotted against time t using (10.65) and (10.66), respectively. A sketch of the two activity curves can be drawn based on a few important features or anchor points shown on the curves. The following features of P→D→G radioactive decay series should be considered:
, respectively, are shown in Fig. 10.3 plotted against time t using (10.65) and (10.66), respectively. A sketch of the two activity curves can be drawn based on a few important features or anchor points shown on the curves. The following features of P→D→G radioactive decay series should be considered:
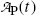 and
and 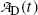 , respectively, are shown in Fig. 10.3 plotted against time t using (10.65) and (10.66), respectively. A sketch of the two activity curves can be drawn based on a few important features or anchor points shown on the curves. The following features of P→D→G radioactive decay series should be considered:
, respectively, are shown in Fig. 10.3 plotted against time t using (10.65) and (10.66), respectively. A sketch of the two activity curves can be drawn based on a few important features or anchor points shown on the curves. The following features of P→D→G radioactive decay series should be considered:(1)
Parent activity 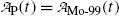 follows exponential decay starting at
follows exponential decay starting at 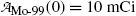 (see Point 1 in Fig. 10.3).
(see Point 1 in Fig. 10.3).
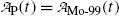 follows exponential decay starting at
follows exponential decay starting at 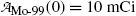 (see Point 1 in Fig. 10.3).
(see Point 1 in Fig. 10.3).
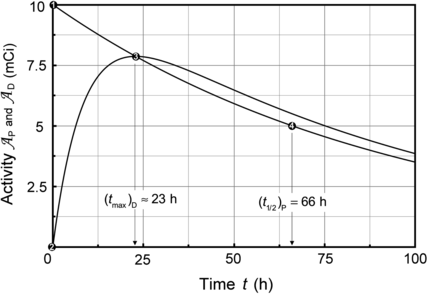
Fig. 10.3
Activity of parent (Mo-99) and daughter (Tc-99m), 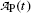 and
and 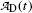 , respectively, against time t. Point (1): initial condition
, respectively, against time t. Point (1): initial condition 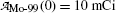 ; point (2): initial condition
; point (2): initial condition 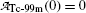 ; point (3) characteristic time (t max)Tc-99m≈23 h and
; point (3) characteristic time (t max)Tc-99m≈23 h and 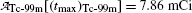 ; and point (4) half-life of Mo-99 (t 1/2)Mo-99=66 h
; and point (4) half-life of Mo-99 (t 1/2)Mo-99=66 h
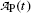 and
and 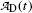 , respectively, against time t. Point (1): initial condition
, respectively, against time t. Point (1): initial condition 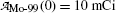 ; point (2): initial condition
; point (2): initial condition 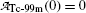 ; point (3) characteristic time (t max)Tc-99m≈23 h and
; point (3) characteristic time (t max)Tc-99m≈23 h and 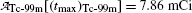 ; and point (4) half-life of Mo-99 (t 1/2)Mo-99=66 h
; and point (4) half-life of Mo-99 (t 1/2)Mo-99=66 h![$$ \frac{\mathrm{d}N_{\mathrm{D}}(t)}{\mathrm{d}t} = N_{\mathrm{P}}(0)\bigl[ - p\lambda _{\mathrm{P}}e^{ - \lambda _{\mathrm{P}}t} - d\lambda _{\mathrm{D}}e^{ - \lambda _{\mathrm{D}}t}\bigr]. $$](/wp-content/uploads/2016/04/A212719_1_En_10_Chapter_Equ35.gif)
![$$ e^{ - \lambda _{\mathrm{P}}t}[ - p\lambda _{\mathrm{P}} - \lambda _{\mathrm{P}} + p\lambda _{\mathrm{D}}] = 0. $$](/wp-content/uploads/2016/04/A212719_1_En_10_Chapter_Equ36.gif)