. An image will be a square-integrable function on 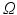 , that is, an element of
, that is, an element of 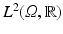 . Let
. Let 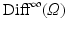 denote the Lie group of smooth diffeomorphisms on
denote the Lie group of smooth diffeomorphisms on 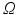 . The Lie algebra for
. The Lie algebra for 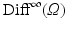 is the space
is the space 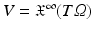 of smooth vector fields on
of smooth vector fields on 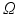 , which is the tangent space at the identity transform. We equip V with the weak Sobolev metric:
, which is the tangent space at the identity transform. We equip V with the weak Sobolev metric:
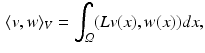
(1)
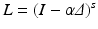 is a symmetric, positive-definite, differential operator for some scalar,
is a symmetric, positive-definite, differential operator for some scalar, 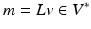 . The notation (m, v) denotes the pairing of a momentum vector
. The notation (m, v) denotes the pairing of a momentum vector 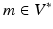 with a tangent vector
with a tangent vector 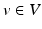 . The metric L is an invertible operator, and
. The metric L is an invertible operator, and 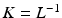 maps the momentum vector
maps the momentum vector 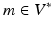 back to the tangent vector
back to the tangent vector 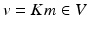 .
.LDDMM: In the LDDMM framework, we will consider diffeomorphisms that are generated by flows of time-varying velocity fields from V. More specifically, consider a time-varying velocity field, ![$$v : [0,1] \rightarrow V$$](/wp-content/uploads/2016/09/A339424_1_En_19_Chapter_IEq17.gif) , then we may define the flow
, then we may define the flow 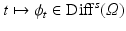 as a solution to the equation
as a solution to the equation
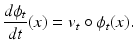 The registration between two images,
The registration between two images, 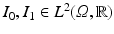 , is the minimizer of the energy,
, is the minimizer of the energy,
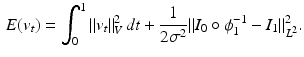
Geodesic Shooting: Given an initial velocity, 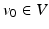 , at
, at 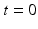 , the geodesic path
, the geodesic path 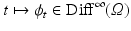 under the right-invariant Riemannian metric (1) is uniquely determined by the Euler-Poincaré equations (EPDiff) [1, 9],
under the right-invariant Riemannian metric (1) is uniquely determined by the Euler-Poincaré equations (EPDiff) [1, 9],
![$$\begin{aligned} \frac{\partial v}{\partial t} = -\mathrm{ad}_{v}^\dagger v&= -K\mathrm{ad}_{v}^*m \nonumber \\&=-K\left[ (Dv)^Tm + Dm\, v + m\,{\text {div}}\,v\right] , \end{aligned}$$](/wp-content/uploads/2016/09/A339424_1_En_19_Chapter_Equ3.gif)
where D denotes the Jacobian matrix, and the operator 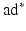 is the dual of the negative Lie bracket of vector fields,
is the dual of the negative Lie bracket of vector fields,
![$$\begin{aligned} \mathrm{ad}_v w = -[v,w] = Dv w - Dw v. \end{aligned}$$](/wp-content/uploads/2016/09/A339424_1_En_19_Chapter_Equ4.gif)
By integrating Eq. (3) forward in time, we generate a time-varying velocity ![$$v_t : [0,1] \rightarrow V$$](/wp-content/uploads/2016/09/A339424_1_En_19_Chapter_IEq24.gif) , which itself is subsequently integrated in time by the rule
, which itself is subsequently integrated in time by the rule 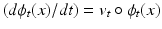 to arrive at the geodesic path,
to arrive at the geodesic path, 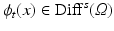 . Details are found in [14, 15]. Noting that the geodesic
. Details are found in [14, 15]. Noting that the geodesic 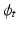 is fully determined by the initial condition
is fully determined by the initial condition 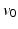 , we can rewrite the LDDMM image matching objective function (2) in terms of the initial velocity
, we can rewrite the LDDMM image matching objective function (2) in terms of the initial velocity 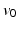 as
as
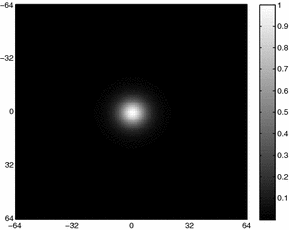
![$$v : [0,1] \rightarrow V$$](/wp-content/uploads/2016/09/A339424_1_En_19_Chapter_IEq17.gif) , then we may define the flow
, then we may define the flow 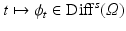 as a solution to the equation
as a solution to the equation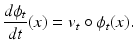
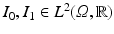 , is the minimizer of the energy,
, is the minimizer of the energy,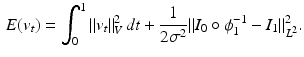
(2)
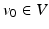 , at
, at 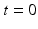 , the geodesic path
, the geodesic path 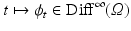 under the right-invariant Riemannian metric (1) is uniquely determined by the Euler-Poincaré equations (EPDiff) [1, 9],
under the right-invariant Riemannian metric (1) is uniquely determined by the Euler-Poincaré equations (EPDiff) [1, 9],![$$\begin{aligned} \frac{\partial v}{\partial t} = -\mathrm{ad}_{v}^\dagger v&= -K\mathrm{ad}_{v}^*m \nonumber \\&=-K\left[ (Dv)^Tm + Dm\, v + m\,{\text {div}}\,v\right] , \end{aligned}$$](/wp-content/uploads/2016/09/A339424_1_En_19_Chapter_Equ3.gif)
(3)
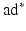 is the dual of the negative Lie bracket of vector fields,
is the dual of the negative Lie bracket of vector fields,![$$\begin{aligned} \mathrm{ad}_v w = -[v,w] = Dv w - Dw v. \end{aligned}$$](/wp-content/uploads/2016/09/A339424_1_En_19_Chapter_Equ4.gif)
(4)
![$$v_t : [0,1] \rightarrow V$$](/wp-content/uploads/2016/09/A339424_1_En_19_Chapter_IEq24.gif) , which itself is subsequently integrated in time by the rule
, which itself is subsequently integrated in time by the rule 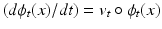 to arrive at the geodesic path,
to arrive at the geodesic path, 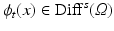 . Details are found in [14, 15]. Noting that the geodesic
. Details are found in [14, 15]. Noting that the geodesic 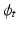 is fully determined by the initial condition
is fully determined by the initial condition 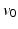 , we can rewrite the LDDMM image matching objective function (2) in terms of the initial velocity
, we can rewrite the LDDMM image matching objective function (2) in terms of the initial velocity 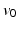 as
as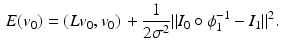
(5)

Fig. 1.
Fourier coefficients of the discretized K operator on a 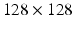 grid, with parameters
grid, with parameters 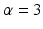 ,
, 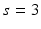 .
.
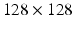 grid, with parameters
grid, with parameters 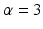 ,
, 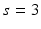 .
.3 Finite-Dimensional Lie Algebras of Diffeomorphism
While the Lie algebra 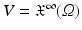 is an infinite-dimensional vector space, we must of course approximate smooth vector fields in V with finite-dimensional discretizations in order to represent them on a computer. In this section, we show that careful choices for the discretization of vector fields and their corresponding Lie brackets leads to a representation that is itself a finite-dimensional Lie algebra. The key observation is that the K operator is a low-pass filter, and as such, suppresses high frequency components in the velocity fields (see, for example, Fig. 1). As the K operator appears as the last operation on the right-hand side of the EPDiff Eq. (3), we can see that the velocity fields in the geodesic evolution do not develop high frequency components. This suggests that a standard implementation of geodesic shooting, using high-resolution velocity fields, wastes a lot of effort computing the high frequency components, which just end up being forced to zero by K. Instead, we propose to use a low-dimensional discretization of velocity fields as bandlimited signals in the Fourier domain.
is an infinite-dimensional vector space, we must of course approximate smooth vector fields in V with finite-dimensional discretizations in order to represent them on a computer. In this section, we show that careful choices for the discretization of vector fields and their corresponding Lie brackets leads to a representation that is itself a finite-dimensional Lie algebra. The key observation is that the K operator is a low-pass filter, and as such, suppresses high frequency components in the velocity fields (see, for example, Fig. 1). As the K operator appears as the last operation on the right-hand side of the EPDiff Eq. (3), we can see that the velocity fields in the geodesic evolution do not develop high frequency components. This suggests that a standard implementation of geodesic shooting, using high-resolution velocity fields, wastes a lot of effort computing the high frequency components, which just end up being forced to zero by K. Instead, we propose to use a low-dimensional discretization of velocity fields as bandlimited signals in the Fourier domain.
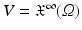 is an infinite-dimensional vector space, we must of course approximate smooth vector fields in V with finite-dimensional discretizations in order to represent them on a computer. In this section, we show that careful choices for the discretization of vector fields and their corresponding Lie brackets leads to a representation that is itself a finite-dimensional Lie algebra. The key observation is that the K operator is a low-pass filter, and as such, suppresses high frequency components in the velocity fields (see, for example, Fig. 1). As the K operator appears as the last operation on the right-hand side of the EPDiff Eq. (3), we can see that the velocity fields in the geodesic evolution do not develop high frequency components. This suggests that a standard implementation of geodesic shooting, using high-resolution velocity fields, wastes a lot of effort computing the high frequency components, which just end up being forced to zero by K. Instead, we propose to use a low-dimensional discretization of velocity fields as bandlimited signals in the Fourier domain.
is an infinite-dimensional vector space, we must of course approximate smooth vector fields in V with finite-dimensional discretizations in order to represent them on a computer. In this section, we show that careful choices for the discretization of vector fields and their corresponding Lie brackets leads to a representation that is itself a finite-dimensional Lie algebra. The key observation is that the K operator is a low-pass filter, and as such, suppresses high frequency components in the velocity fields (see, for example, Fig. 1). As the K operator appears as the last operation on the right-hand side of the EPDiff Eq. (3), we can see that the velocity fields in the geodesic evolution do not develop high frequency components. This suggests that a standard implementation of geodesic shooting, using high-resolution velocity fields, wastes a lot of effort computing the high frequency components, which just end up being forced to zero by K. Instead, we propose to use a low-dimensional discretization of velocity fields as bandlimited signals in the Fourier domain.More specifically, let 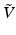 denote the space of bandlimited velocity fields on
denote the space of bandlimited velocity fields on 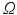 , with frequency bounds
, with frequency bounds 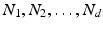 in each of the dimensions of
in each of the dimensions of 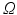 . It will be convenient to represent an element
. It will be convenient to represent an element 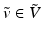 in the Fourier domain. That is, let
in the Fourier domain. That is, let 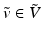 be a multidimensional array:
be a multidimensional array: 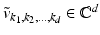 , where
, where 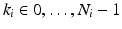 is the frequency index along the ith axis. Note that to ensure
is the frequency index along the ith axis. Note that to ensure 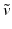 represents a real-valued vector field in the spatial domain, we have the constraint that
represents a real-valued vector field in the spatial domain, we have the constraint that 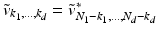 , where
, where 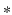 denotes the complex conjugate. There is a natural inclusion mapping,
denotes the complex conjugate. There is a natural inclusion mapping, 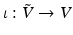 , of
, of 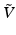 into the space V of smooth vector fields, given by the Fourier series expansion:
into the space V of smooth vector fields, given by the Fourier series expansion:
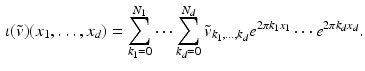
Next, we define an operator that is a discrete analog of (4), the Lie bracket on continuous vector fields. First, we will denote by 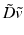 the central difference Jacobian matrix of a discrete vector field,
the central difference Jacobian matrix of a discrete vector field, 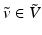 . This can be computed in the discrete Fourier domain as a tensor product
. This can be computed in the discrete Fourier domain as a tensor product 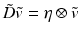 , where
, where 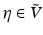 is given by
is given by
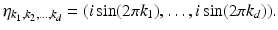 Second, we note that pointwise multiplication of matrix and vector field in the spatial domain corresponds to convolution in the Fourier domain. Because convolution between two bandlimited signals does not preserve the bandlimit, we must follow a convolution operation by truncation back to the bandlimits,
Second, we note that pointwise multiplication of matrix and vector field in the spatial domain corresponds to convolution in the Fourier domain. Because convolution between two bandlimited signals does not preserve the bandlimit, we must follow a convolution operation by truncation back to the bandlimits, 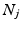 , in each dimension. We denote this truncated convolution operator between a matrix and a vector field as
, in each dimension. We denote this truncated convolution operator between a matrix and a vector field as  . Now we are ready to define our discrete bracket operator for any two vectors
. Now we are ready to define our discrete bracket operator for any two vectors 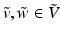 as
as
![$$\begin{aligned}{}[\tilde{v}, \, \tilde{w}] = (\tilde{D} \tilde{v}) \star \tilde{w} - (\tilde{D} \tilde{w}) \star \tilde{v}. \end{aligned}$$](/wp-content/uploads/2016/09/A339424_1_En_19_Chapter_Equ7.gif)
The next theorem proves that this operation satisfies the properties to be a Lie bracket on 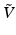 .
.
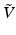 denote the space of bandlimited velocity fields on
denote the space of bandlimited velocity fields on 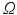 , with frequency bounds
, with frequency bounds 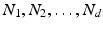 in each of the dimensions of
in each of the dimensions of 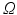 . It will be convenient to represent an element
. It will be convenient to represent an element 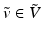 in the Fourier domain. That is, let
in the Fourier domain. That is, let 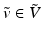 be a multidimensional array:
be a multidimensional array: 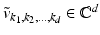 , where
, where 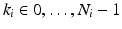 is the frequency index along the ith axis. Note that to ensure
is the frequency index along the ith axis. Note that to ensure 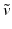 represents a real-valued vector field in the spatial domain, we have the constraint that
represents a real-valued vector field in the spatial domain, we have the constraint that 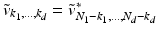 , where
, where 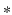 denotes the complex conjugate. There is a natural inclusion mapping,
denotes the complex conjugate. There is a natural inclusion mapping, 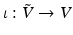 , of
, of 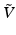 into the space V of smooth vector fields, given by the Fourier series expansion:
into the space V of smooth vector fields, given by the Fourier series expansion: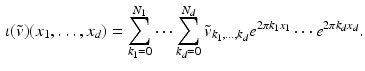
(6)
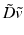 the central difference Jacobian matrix of a discrete vector field,
the central difference Jacobian matrix of a discrete vector field, 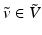 . This can be computed in the discrete Fourier domain as a tensor product
. This can be computed in the discrete Fourier domain as a tensor product 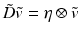 , where
, where 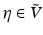 is given by
is given by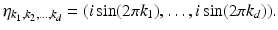
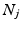 , in each dimension. We denote this truncated convolution operator between a matrix and a vector field as
, in each dimension. We denote this truncated convolution operator between a matrix and a vector field as 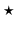 . Now we are ready to define our discrete bracket operator for any two vectors
. Now we are ready to define our discrete bracket operator for any two vectors 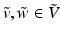 as
as![$$\begin{aligned}{}[\tilde{v}, \, \tilde{w}] = (\tilde{D} \tilde{v}) \star \tilde{w} - (\tilde{D} \tilde{w}) \star \tilde{v}. \end{aligned}$$](/wp-content/uploads/2016/09/A339424_1_En_19_Chapter_Equ7.gif)
(7)
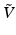 .
.Theorem 1
The vector space 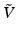 , when equipped with the bracket operation (7), is a finite-dimensional Lie algebra. That is to say,
, when equipped with the bracket operation (7), is a finite-dimensional Lie algebra. That is to say, 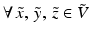 and
and 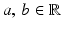 , the following properties are satisfied:
, the following properties are satisfied:
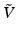 , when equipped with the bracket operation (7), is a finite-dimensional Lie algebra. That is to say,
, when equipped with the bracket operation (7), is a finite-dimensional Lie algebra. That is to say, 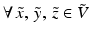 and
and 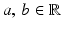 , the following properties are satisfied:
, the following properties are satisfied:(a)
Linearity: ![$$[a \tilde{x} + b \tilde{y}, \, \tilde{z}] = a \, [\tilde{x}, \, \tilde{z}] + b \, [\tilde{y}, \, \tilde{z}]$$](/wp-content/uploads/2016/09/A339424_1_En_19_Chapter_IEq58.gif) ,
,
![$$[a \tilde{x} + b \tilde{y}, \, \tilde{z}] = a \, [\tilde{x}, \, \tilde{z}] + b \, [\tilde{y}, \, \tilde{z}]$$](/wp-content/uploads/2016/09/A339424_1_En_19_Chapter_IEq58.gif) ,
,(b)
Anticommutativity: ![$$[\tilde{x}, \, \tilde{y}]=-[\tilde{y}, \, \tilde{x}]$$](/wp-content/uploads/2016/09/A339424_1_En_19_Chapter_IEq59.gif) ,
,
![$$[\tilde{x}, \, \tilde{y}]=-[\tilde{y}, \, \tilde{x}]$$](/wp-content/uploads/2016/09/A339424_1_En_19_Chapter_IEq59.gif) ,
,(c)
Jacobi identity: ![$$[\tilde{x}, \, [\tilde{y}, \, \tilde{z}]] + [\tilde{z}, \, [\tilde{x}, \, \tilde{y}]] + [\tilde{y}, \, [\tilde{z}, \, \tilde{x}]] = 0$$](/wp-content/uploads/2016/09/A339424_1_En_19_Chapter_IEq60.gif) .
.
![$$[\tilde{x}, \, [\tilde{y}, \, \tilde{z}]] + [\tilde{z}, \, [\tilde{x}, \, \tilde{y}]] + [\tilde{y}, \, [\tilde{z}, \, \tilde{x}]] = 0$$](/wp-content/uploads/2016/09/A339424_1_En_19_Chapter_IEq60.gif) .
.Proof
Linearity and anticommutativity are immediate. We have

![$$\begin{aligned}{}[a \tilde{x} + b \tilde{y}, \, \tilde{z}]&= \tilde{D} (a\tilde{x} + b\tilde{y})\star \tilde{z}- \tilde{D} \tilde{z} \star (a\tilde{x} + b\tilde{y}) \\&= a(\tilde{D} \tilde{x}\star \tilde{z}- \tilde{D} \tilde{z} \star \tilde{x}) + b(\tilde{D} \tilde{y} \star \tilde{z} - \tilde{D} \tilde{z} \star \tilde{y}) \\&= a [\tilde{x}, \, \tilde{z}] + b [\tilde{y}, \, \tilde{z}], \end{aligned}$$](/wp-content/uploads/2016/09/A339424_1_En_19_Chapter_Equ18.gif)




