.
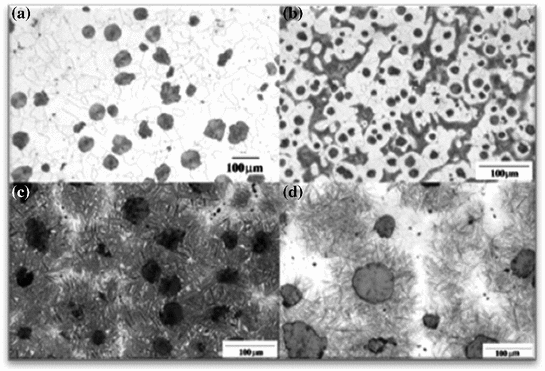
Fig. 1
a Ferritic DCI; b ferritic-pearlitic DCI; c and d two different ADI
Image analysis may help in the identification and characterization of damage. The aim is to obtain an objective evaluation of damage without the supervision of an operator. The main difficulty is related with the quality of the data that may be corrupted for the presence of dust or scratches or non uniform illumination. By considering the image before the damage took place, it would be possible to decide a suitable preprocessing procedure to reduce the effects of degradation. In particular for the analyzed data a second order statistic filter and an adaptive histogram equalization were the main image analysis operations adopted, as will be shown in the next section. The chapter is organized as follows: in the first part of the Material and Methods Section the damaging micromechanisms acting on the investigated alloy are described, whereas in the second part the image analysis procedure adopted is outlined. In the Numerical Results and Comments Section the damaging morphologies in graphite nodules are identified and a quantitative evaluation of damage is proposed.
2 Materials and Methods
In this section, the investigated alloy and the damaging micromechanisms are described, along with the image analysis procedure adopted and the damage evaluation criteria considered.
2.1 Materials
Investigated DCI chemical composition is shown in Table 1. It is characterized by a fully ferritic microstructure and by a very high graphite elements nodularity (higher than 85 %, with a volume fraction of graphite elements of about 9–10 %; 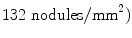 .
.
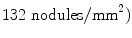 .
.Table 1
Investigated fully ferritic DCI chemical composition (GJS 350-22)
C | Si | Mn | S | P | Cu | Cr | Mg | Sn |
|---|---|---|---|---|---|---|---|---|
3.62 | 2.72 | 0.19 | 0.011 | 0.021 | 0.019 | 0.031 | 0.047 | 0.011 |
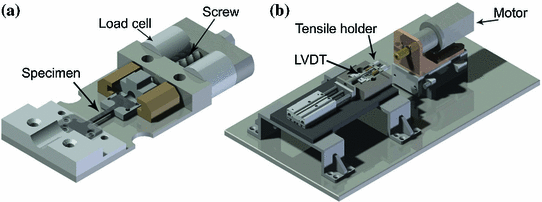
Fatigue tests were performed considering microtensile specimens  . Specimens were ground and polished and fatigue loaded intermittently with a tensile holder and observed in situ using a Scanning Electron Microscope (SEM), considering 20 graphite elements. During fatigue tests, specimens deformation and applied load were measured by means of a Linear Variable Differential Transformer (LVDT) and two miniature load cells (10 kN each), respectively. Figures 2a, b show the tensile holder and the tensile test machine, respectively.
. Specimens were ground and polished and fatigue loaded intermittently with a tensile holder and observed in situ using a Scanning Electron Microscope (SEM), considering 20 graphite elements. During fatigue tests, specimens deformation and applied load were measured by means of a Linear Variable Differential Transformer (LVDT) and two miniature load cells (10 kN each), respectively. Figures 2a, b show the tensile holder and the tensile test machine, respectively.
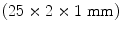 . Specimens were ground and polished and fatigue loaded intermittently with a tensile holder and observed in situ using a Scanning Electron Microscope (SEM), considering 20 graphite elements. During fatigue tests, specimens deformation and applied load were measured by means of a Linear Variable Differential Transformer (LVDT) and two miniature load cells (10 kN each), respectively. Figures 2a, b show the tensile holder and the tensile test machine, respectively.
. Specimens were ground and polished and fatigue loaded intermittently with a tensile holder and observed in situ using a Scanning Electron Microscope (SEM), considering 20 graphite elements. During fatigue tests, specimens deformation and applied load were measured by means of a Linear Variable Differential Transformer (LVDT) and two miniature load cells (10 kN each), respectively. Figures 2a, b show the tensile holder and the tensile test machine, respectively.
Fig. 2
a Removable holder with microtensile specimen; b fatigue testing machine
Fatigue tests were repeated three times and performed under load control conditions 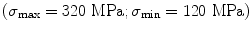 , with a loading frequency of 0.03 Hz. In order to perform scanning electron microscope (SEM) observations, fatigue loading was stopped every 1000 cycles (near final rupture observations frequency is higher).
, with a loading frequency of 0.03 Hz. In order to perform scanning electron microscope (SEM) observations, fatigue loading was stopped every 1000 cycles (near final rupture observations frequency is higher).
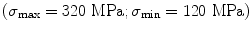 , with a loading frequency of 0.03 Hz. In order to perform scanning electron microscope (SEM) observations, fatigue loading was stopped every 1000 cycles (near final rupture observations frequency is higher).
, with a loading frequency of 0.03 Hz. In order to perform scanning electron microscope (SEM) observations, fatigue loading was stopped every 1000 cycles (near final rupture observations frequency is higher).Focusing the graphite nodules, the damage usually follows a sort of “onion-like” sequence, with the damage that became more and more evident with the cycles number (Fig. 3). Seldom, a crack in the nodule center is observed, probably corresponding to the nucleation site, but the main damaging micromechanism is the one shown in Fig. 3.
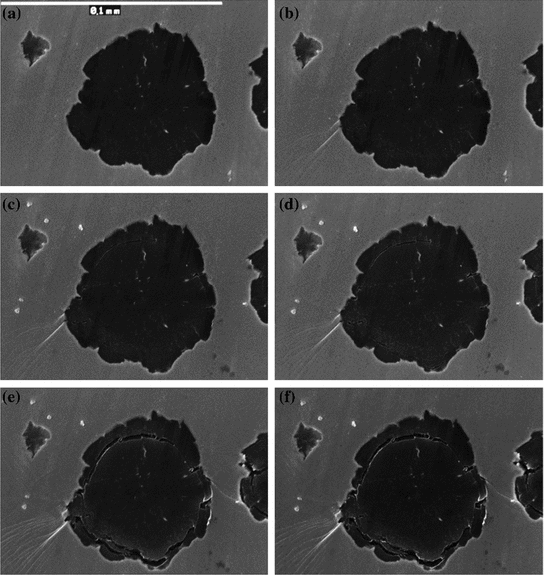

Fig. 3
Graphite nodule damaging evolution. SEM in situ surface analysis corresponding to the following loading cycles: a 1; b 14100; c 38300; d 40100; e 46000; f 48100 cycles
2.2 Methods: Image Analysis
As already pointed out in the Introduction, image analysis may help in the identification and quantification of the effects of damage. At a first sight, its effects appear evident but an automatic detection results difficult due to the presence of scratches and dust. Moreover different kind of damage effects may be present in the same specimen, each of them requiring a different identification procedure. In this chapter the interest is focused on the effects that present the shape of thin curvilinear rectangular, whereas a darker kernel, mainly positioned in the center of the damaged specimen, will not be analyzed. The operation that may help in damage identification is the segmentation; as well known, it is the partition of the image into regions homogeneous with respect to a chosen property, [8]. For the data of this application the objects of interest are the darkest elements of the image, therefore a segmentation with respect to the gray level is required.
The elements of interest are generally not neatly separated one each other and from the background, see Fig. 4 as an example. Therefore before proceeding with the segmentation step a suitable preprocessing is advisable.
First the original data is filtered by a 2-D statistic filter: the image is partitioned into square domains of chosen size and each element in the domain is replaced by the m-order element in the sorted set of neighbors identified by the nonzero elements in the same region. The result is a more uniform image, thus helping in avoiding isolated and small region detection.
The obtained image wasn’t yet suitable for the segmentation, and it was necessary to enhance the contrast by a contrast-limited adaptive histogram equalization; again the image is partitioned in tiles, whose contrast is enhanced in order to obtain an histogram of each tile as much as possible similar to a chosen distribution. In the present application the uniform distribution was assumed. This operation was performed without enhancing the darker kernel damage. Finally a gamma correction operation was useful for illumination problems due to the image acquisition procedure. The processed data was segmented by using the Otsu method, [13]. This method was chosen for its effectiveness, even if, as pointed out in [7], also the discrete level set method [6] yielded satisfactory results. The Otsu method is based on the assumption that the histogram of the data is bi-modal and therefore two classes of pixels are considered, the object and the background. The optimal threshold is obtained by minimizing the intra-class variance:
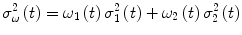 where
where 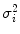 are the variances of the classes and the weights
are the variances of the classes and the weights 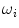 represent the probabilities of the two classes separated by the threshold
represent the probabilities of the two classes separated by the threshold 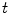 .
.
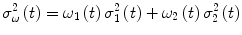
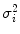 are the variances of the classes and the weights
are the variances of the classes and the weights 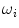 represent the probabilities of the two classes separated by the threshold
represent the probabilities of the two classes separated by the threshold 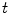 .
.An n-level segmentation, with n = 8, was needed; the damage was identified among the objects with the lowest gray level.
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree



