, the LDDMM energy functional is defined as:
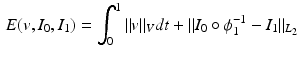
(1)
![$$v \in L^2([0,1], V)$$](/wp-content/uploads/2016/09/A339424_1_En_59_Chapter_IEq2.gif) is a time dependent velocity field drawn from the reproducing kernel Hilbert space (RKHS) V. The RKHS is specified by the choice of kernel K, and the inner product in V is then given by
is a time dependent velocity field drawn from the reproducing kernel Hilbert space (RKHS) V. The RKHS is specified by the choice of kernel K, and the inner product in V is then given by 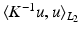 for any
for any 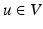 . The transformation
. The transformation 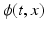 is given by the flow of the velocity v(t, x) through the ODE:
is given by the flow of the velocity v(t, x) through the ODE: 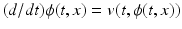 , with initial condition
, with initial condition 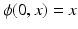 . v(t, x) and
. v(t, x) and 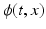 will be written as
will be written as 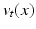 and
and 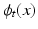 . The minimizer of (1) is considered the optimal
. The minimizer of (1) is considered the optimal 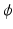 for the registration of
for the registration of 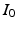 and
and 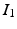 .
.The second term on the right hand side of (1) is a quantitative assessment of the similarity between the images 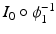 and
and 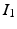 , whereas the first term is the geodesic energy of the flow of
, whereas the first term is the geodesic energy of the flow of 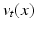 . For suitable choices of K,
. For suitable choices of K, 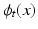 is always a diffeomorphism [10]; hence, (1) defines
is always a diffeomorphism [10]; hence, (1) defines 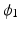 to be the transformation that best matches
to be the transformation that best matches 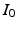 and
and 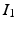 such that
such that 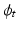 is a geodesic in a space of diffeomorphisms specified by the choice of K. As
is a geodesic in a space of diffeomorphisms specified by the choice of K. As 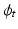 is a geodesic when
is a geodesic when 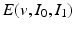 is optimal,
is optimal, 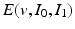 defines a metric distance
defines a metric distance 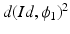 in the space of diffeomorphisms. This can also be considered a metric
in the space of diffeomorphisms. This can also be considered a metric 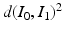 on the orbit given by the group action of the space of diffeomorphisms on the template image
on the orbit given by the group action of the space of diffeomorphisms on the template image 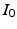 .
.
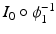 and
and 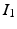 , whereas the first term is the geodesic energy of the flow of
, whereas the first term is the geodesic energy of the flow of 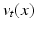 . For suitable choices of K,
. For suitable choices of K, 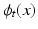 is always a diffeomorphism [10]; hence, (1) defines
is always a diffeomorphism [10]; hence, (1) defines 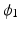 to be the transformation that best matches
to be the transformation that best matches 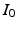 and
and 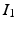 such that
such that 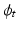 is a geodesic in a space of diffeomorphisms specified by the choice of K. As
is a geodesic in a space of diffeomorphisms specified by the choice of K. As 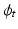 is a geodesic when
is a geodesic when 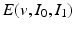 is optimal,
is optimal, 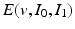 defines a metric distance
defines a metric distance 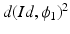 in the space of diffeomorphisms. This can also be considered a metric
in the space of diffeomorphisms. This can also be considered a metric 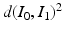 on the orbit given by the group action of the space of diffeomorphisms on the template image
on the orbit given by the group action of the space of diffeomorphisms on the template image 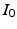 .
.Background, Geodesic Shooting Algorithm: Several approaches to optimizing (1) have been proposed. In this paper we use the geodesic shooting approach [6, 12], which we now review. The kernel K can also be considered a mapping between 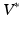 , the space of linear functionals on V, and V itself. Note that
, the space of linear functionals on V, and V itself. Note that 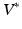 is also a Hilbert space. An Element of
is also a Hilbert space. An Element of 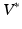 is called a momentum. Hence for any momentum
is called a momentum. Hence for any momentum 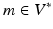 there is some
there is some 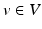 such that
such that 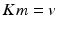 and
and 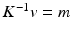 .
.
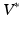 , the space of linear functionals on V, and V itself. Note that
, the space of linear functionals on V, and V itself. Note that 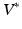 is also a Hilbert space. An Element of
is also a Hilbert space. An Element of 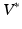 is called a momentum. Hence for any momentum
is called a momentum. Hence for any momentum 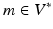 there is some
there is some 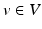 such that
such that 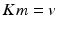 and
and 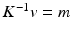 .
.An optimal solution to (1) specifies a geodesic, which is uniquely determined by its initial velocity 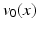 , or equivalently, its initial momentum
, or equivalently, its initial momentum 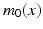 .
. 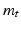 for all t, and hence
for all t, and hence 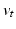 and
and 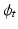 , can then be determined by solving the co-adjoint equation [6]:
, can then be determined by solving the co-adjoint equation [6]: 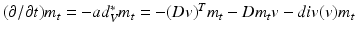 , where D denotes the Jacobian operator and div(.) the divergence operator. If the initial momentum is assumed to be proportional to the template image gradient, that is
, where D denotes the Jacobian operator and div(.) the divergence operator. If the initial momentum is assumed to be proportional to the template image gradient, that is 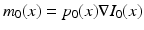 for some scalar field
for some scalar field 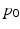 , the adjoint equation can be separated into a disjoint system of differential equations for
, the adjoint equation can be separated into a disjoint system of differential equations for 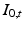 and
and 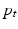 respectively [12], where
respectively [12], where 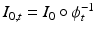 . Considering these equations and the gradient of (1) with respect to
. Considering these equations and the gradient of (1) with respect to 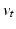 , we arrive at a system of partial differential equations that completely specifies
, we arrive at a system of partial differential equations that completely specifies 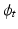 given initial conditions
given initial conditions 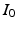 and
and 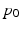 (
(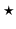 denotes convolution):
denotes convolution):
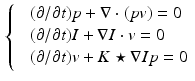
With this in mind, (1) is replaced with a functional of the initial momentum exclusively:
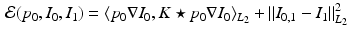
and optimization proceeds within 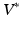 only. In order to optimize (3) by gradient descent, we need the gradient of (3) with respect to
only. In order to optimize (3) by gradient descent, we need the gradient of (3) with respect to 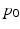 , subject to the geodesic shooting constraints (2). This naturally gives way to an optimal control problem. Time dependent Lagrange multipliers
, subject to the geodesic shooting constraints (2). This naturally gives way to an optimal control problem. Time dependent Lagrange multipliers 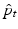 ,
, 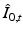 , and
, and 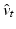 enable us to write an augmented functional for (3) incorporating the constraints (2):
enable us to write an augmented functional for (3) incorporating the constraints (2):
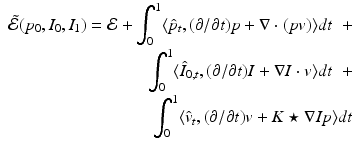
The first variation of (4) gives the gradient of (3) subject to (2):
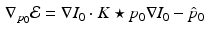
where 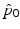 is specified by a system of partial differential equations solved backward in time termed the adjoint system:
is specified by a system of partial differential equations solved backward in time termed the adjoint system:
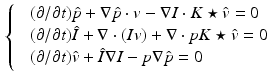
with initial conditions 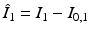 and
and 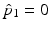 . The gradient descent proceeds by solving the system (2) forward in time to acquire
. The gradient descent proceeds by solving the system (2) forward in time to acquire 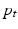 ,
, 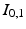 , and
, and 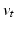 for a sufficiently dense sampling of
for a sufficiently dense sampling of ![$$t \in [0,1]$$](/wp-content/uploads/2016/09/A339424_1_En_59_Chapter_IEq62.gif) , then solving (6) backward in time to acquire
, then solving (6) backward in time to acquire 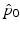 .
. 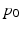 is then updated with (5), and the process is repeated until convergence.
is then updated with (5), and the process is repeated until convergence.
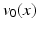 , or equivalently, its initial momentum
, or equivalently, its initial momentum 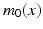 .
. 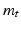 for all t, and hence
for all t, and hence 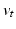 and
and 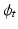 , can then be determined by solving the co-adjoint equation [6]:
, can then be determined by solving the co-adjoint equation [6]: 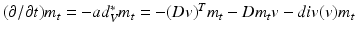 , where D denotes the Jacobian operator and div(.) the divergence operator. If the initial momentum is assumed to be proportional to the template image gradient, that is
, where D denotes the Jacobian operator and div(.) the divergence operator. If the initial momentum is assumed to be proportional to the template image gradient, that is 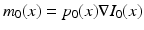 for some scalar field
for some scalar field 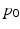 , the adjoint equation can be separated into a disjoint system of differential equations for
, the adjoint equation can be separated into a disjoint system of differential equations for 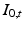 and
and 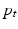 respectively [12], where
respectively [12], where 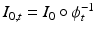 . Considering these equations and the gradient of (1) with respect to
. Considering these equations and the gradient of (1) with respect to 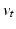 , we arrive at a system of partial differential equations that completely specifies
, we arrive at a system of partial differential equations that completely specifies 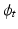 given initial conditions
given initial conditions 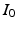 and
and 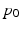 (
(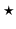 denotes convolution):
denotes convolution):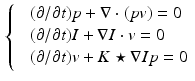
(2)
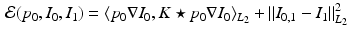
(3)
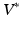 only. In order to optimize (3) by gradient descent, we need the gradient of (3) with respect to
only. In order to optimize (3) by gradient descent, we need the gradient of (3) with respect to 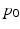 , subject to the geodesic shooting constraints (2). This naturally gives way to an optimal control problem. Time dependent Lagrange multipliers
, subject to the geodesic shooting constraints (2). This naturally gives way to an optimal control problem. Time dependent Lagrange multipliers 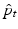 ,
, 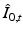 , and
, and 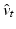 enable us to write an augmented functional for (3) incorporating the constraints (2):
enable us to write an augmented functional for (3) incorporating the constraints (2):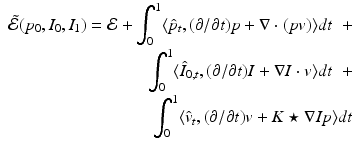
(4)
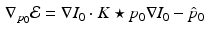
(5)
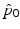 is specified by a system of partial differential equations solved backward in time termed the adjoint system:
is specified by a system of partial differential equations solved backward in time termed the adjoint system: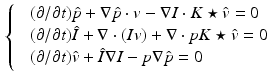
(6)
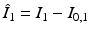 and
and 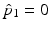 . The gradient descent proceeds by solving the system (2) forward in time to acquire
. The gradient descent proceeds by solving the system (2) forward in time to acquire 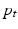 ,
, 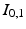 , and
, and 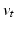 for a sufficiently dense sampling of
for a sufficiently dense sampling of ![$$t \in [0,1]$$](/wp-content/uploads/2016/09/A339424_1_En_59_Chapter_IEq62.gif) , then solving (6) backward in time to acquire
, then solving (6) backward in time to acquire 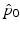 .
. 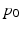 is then updated with (5), and the process is repeated until convergence.
is then updated with (5), and the process is repeated until convergence.Group-wise Similarity Prior: We consider the case where we are given N longitudinal image pairs 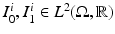 ,
, ![$$i \in [1,2,...,N]$$](/wp-content/uploads/2016/09/A339424_1_En_59_Chapter_IEq66.gif) , all taken approximately the same time interval apart. We take
, all taken approximately the same time interval apart. We take 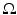 to be the unit cube with periodic boundary conditions, and the time interval to be [0, 1]. Additionally, we are given N transformations
to be the unit cube with periodic boundary conditions, and the time interval to be [0, 1]. Additionally, we are given N transformations 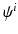 mapping the initial images
mapping the initial images 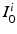 to a Minimal Deformation Template (MDT) coordinate system, that is,
to a Minimal Deformation Template (MDT) coordinate system, that is, 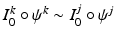 for all k and j. To consider all N registrations simultaneously with no modification to the geodesic shooting approach, we could write
for all k and j. To consider all N registrations simultaneously with no modification to the geodesic shooting approach, we could write 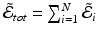 where
where 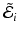 is eq. (3) for the ith image pair. The first variation of
is eq. (3) for the ith image pair. The first variation of 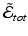 with respect to an initial momentum
with respect to an initial momentum 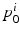 will only include terms for the ith pair, that is, the N transformations are decoupled. However, we would like the N transformations to explore the space of diffeomorphisms as a group. We couple them by considering equations of the form:
will only include terms for the ith pair, that is, the N transformations are decoupled. However, we would like the N transformations to explore the space of diffeomorphisms as a group. We couple them by considering equations of the form:
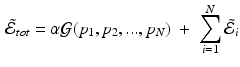
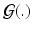 is intended to enforce some criteria that we may think all
is intended to enforce some criteria that we may think all 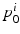 must satisfy. In this paper, we consider longitudinal studies where all N image pairs come from patients in the same diagnostic group, where a predictable distribution of volume change is known to occur. Because
must satisfy. In this paper, we consider longitudinal studies where all N image pairs come from patients in the same diagnostic group, where a predictable distribution of volume change is known to occur. Because 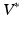 is a Hilbert space, we can calculate statistical moments in this space in an ordinary manner, being careful to spatially normalize the
is a Hilbert space, we can calculate statistical moments in this space in an ordinary manner, being careful to spatially normalize the 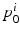 to a MDT coordinate system using coadjoint transport [15]. First, let
to a MDT coordinate system using coadjoint transport [15]. First, let 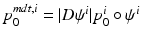 , be the ith initial momentum in the MDT coordinate system. Let
, be the ith initial momentum in the MDT coordinate system. Let 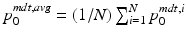 be the sample average initial momentum in MDT coordinates. Let
be the sample average initial momentum in MDT coordinates. Let 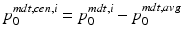 be the mean centered initial momentum for image pair i in MDT coordinates, and let
be the mean centered initial momentum for image pair i in MDT coordinates, and let ![$$A = [p^{mdt,cen,1}_0, p^{mdt,cen,2}_0,...,p^{mdt,cen,N}_0]^T$$](/wp-content/uploads/2016/09/A339424_1_En_59_Chapter_IEq82.gif) be the mean centered design matrix for all initial momenta in MDT coordinates. We take
be the mean centered design matrix for all initial momenta in MDT coordinates. We take 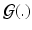 to be:
to be:
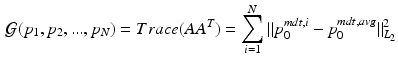
the trace of the sample inner-product matrix for 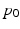 .
.
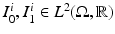 ,
, ![$$i \in [1,2,...,N]$$](/wp-content/uploads/2016/09/A339424_1_En_59_Chapter_IEq66.gif) , all taken approximately the same time interval apart. We take
, all taken approximately the same time interval apart. We take  to be the unit cube with periodic boundary conditions, and the time interval to be [0, 1]. Additionally, we are given N transformations
to be the unit cube with periodic boundary conditions, and the time interval to be [0, 1]. Additionally, we are given N transformations 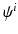 mapping the initial images
mapping the initial images 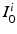 to a Minimal Deformation Template (MDT) coordinate system, that is,
to a Minimal Deformation Template (MDT) coordinate system, that is, 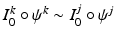 for all k and j. To consider all N registrations simultaneously with no modification to the geodesic shooting approach, we could write
for all k and j. To consider all N registrations simultaneously with no modification to the geodesic shooting approach, we could write 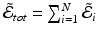 where
where 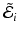 is eq. (3) for the ith image pair. The first variation of
is eq. (3) for the ith image pair. The first variation of 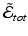 with respect to an initial momentum
with respect to an initial momentum 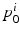 will only include terms for the ith pair, that is, the N transformations are decoupled. However, we would like the N transformations to explore the space of diffeomorphisms as a group. We couple them by considering equations of the form:
will only include terms for the ith pair, that is, the N transformations are decoupled. However, we would like the N transformations to explore the space of diffeomorphisms as a group. We couple them by considering equations of the form: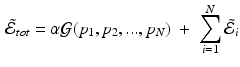
(7)
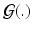 is intended to enforce some criteria that we may think all
is intended to enforce some criteria that we may think all 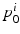 must satisfy. In this paper, we consider longitudinal studies where all N image pairs come from patients in the same diagnostic group, where a predictable distribution of volume change is known to occur. Because
must satisfy. In this paper, we consider longitudinal studies where all N image pairs come from patients in the same diagnostic group, where a predictable distribution of volume change is known to occur. Because 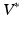 is a Hilbert space, we can calculate statistical moments in this space in an ordinary manner, being careful to spatially normalize the
is a Hilbert space, we can calculate statistical moments in this space in an ordinary manner, being careful to spatially normalize the 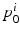 to a MDT coordinate system using coadjoint transport [15]. First, let
to a MDT coordinate system using coadjoint transport [15]. First, let 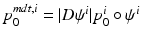 , be the ith initial momentum in the MDT coordinate system. Let
, be the ith initial momentum in the MDT coordinate system. Let 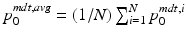 be the sample average initial momentum in MDT coordinates. Let
be the sample average initial momentum in MDT coordinates. Let 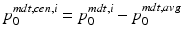 be the mean centered initial momentum for image pair i in MDT coordinates, and let
be the mean centered initial momentum for image pair i in MDT coordinates, and let ![$$A = [p^{mdt,cen,1}_0, p^{mdt,cen,2}_0,...,p^{mdt,cen,N}_0]^T$$](/wp-content/uploads/2016/09/A339424_1_En_59_Chapter_IEq82.gif) be the mean centered design matrix for all initial momenta in MDT coordinates. We take
be the mean centered design matrix for all initial momenta in MDT coordinates. We take 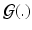 to be:
to be: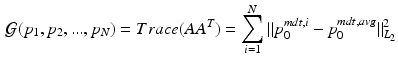
(8)
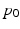 .
.First we consider the rightmost form of (8). We see that this term maintains a group-wise average of the initial momentum, and requires that all momenta be close to this average. This is similar to hierarchical latent variable models that maintain a group-wise representation of the data and constrain updates to predictions to be similar to this representation.
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree




