(1)
Department of MRI, Medical Center at Siegerland Airport, Burbach, Germany
In low-field MR scanners, some imaging parameters are different from high-field systems. These different characteristics can be of advantage or disadvantage, depending on the imaging situation (Kuhl et al. 2008; Hoult et al. 1986).
5.1 Larmor Frequency and Chemical Shift
The resonance frequency of molecules in a strong external magnetic field is called Larmor frequency ω. The relation between field strength B o and the resonance frequency is given by the Larmor equation:
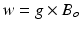 The gyromagnetic ratio for protons is 42.6 MHz/T.
The gyromagnetic ratio for protons is 42.6 MHz/T.
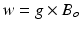
The lower the field strength, the slower the spins rotate around the z-axis. The spin cycle time is therefore increased from 4.6 ms at 1.5 T to 19.7 ms at 0.35 T.
This means that fat-suppressed sequences with opposed-phase technique, where the spins of fat and water have to be in 180° opposite direction, take a longer acquisition time (Schild 2005). The same is true for time-of-flight angiographic sequences (Pavone 1992, Keller and Saloner 1993).
For time-critical sequences with exact phase setting, like MR mammograms, where small time deviations lead to severe signal changes, longer spin cycle time can be advantageous.
Another consequence of lower field strength is that the resulting lower frequent RF signal shows better tissue penetration (Kuhl et al. 2008). Therefore, the homogeneity of the RF magnetic field, the so-called B1 field, is improved, giving better inherent field homogeneity. In high-field MRI > 1.5 T, B1 inhomogeneity is a big issue, which can be compensated only by expensive multi-transmit technology, helpful, but still a compromise.
Furthermore, higher RF increases RF deposition and in consequence tissue heating dramatically (see below), influencing clinical use.
Another consequence of lower field strength is a slightly different resonance frequency between tissues (Peh and Chan 2001). At 1.5 T, fat and water resonance peaks are shifted by 220 Hz. At 0.4 T, the chemical shift is only 66 Hz. With decreased chemical shift, the black bands at fat–water interfaces become smaller (another way would be to increase frequency bandwidth, thus reducing SNR).
Chemical shift, however, is the basic principle for spectroscopic differentiation of substances. MR spectroscopy is inferior in lower-field systems.
Another disadvantage resulting from reduced chemical shift is the insufficient effect of spectral fat saturation (see below).
5.2 Homogeneity
Homogeneity is a decisive parameter for image quality.
Homogeneity of the magnetic field depends on the primary structure of the magnet, in case of low field strength mostly a permanent magnet, and equalization of inhomogeneities, the shimming process.
Optimizing the shimming procedure is of crucial importance to provide optimal imaging results. In any way, it is difficult to achieve the values of a high-field system, particularly using an open design permanent magnet.
Why is homogeneity so important? Spatial encoding is done by superimposing a gradient field and thereby modulating the local field strength. This results in a locally defined resonance frequency. Using a Fourier analysis of the resonance spectrum, each spatial point is represented by a certain resonance frequency. Inhomogeneous magnetic field strength therefore directly influences spatial resolution (Edelstein et al. 1983).
The quantification of homogeneity is regularly measured in parts per million (ppm). A homogeneous field strength for the whole field of view (40 cm) with a deviance of less than 5 ppm measured peak to peak is mandatory for acceptance of an MR system by the public health insurances in Germany (see Chap. 2).
Since lower field strength goes along with a better background homogeneity (Kaufman et al. 1989), it may be more adequate to measure this parameter in absolute values. Absolute homogeneity is given by ppm × field strength (gauss). A homogeneity value of 5 ppm on a 0.35 T (3500 G) system is better than 5 ppm at 1.5 T (15,000 G):
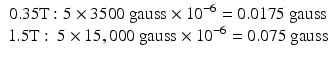 An argument in favor of a relative homogeneity measurement is the fact that spectral fat saturation depends on field strength homogeneity. As said above, at 0.4 T the frequency offset between fat and water is only 66 Hz and at 1.5 T 220 Hz. Spectral saturation of fat protons is an important tool for clinical imaging. The small frequency difference makes spectral fat saturation difficult in low-field imaging and requires even more homogeneity. To ensure reliable fat saturation, the absolute homogeneity needs to be proportional to field strength. The same is true for spectroscopic analysis.
An argument in favor of a relative homogeneity measurement is the fact that spectral fat saturation depends on field strength homogeneity. As said above, at 0.4 T the frequency offset between fat and water is only 66 Hz and at 1.5 T 220 Hz. Spectral saturation of fat protons is an important tool for clinical imaging. The small frequency difference makes spectral fat saturation difficult in low-field imaging and requires even more homogeneity. To ensure reliable fat saturation, the absolute homogeneity needs to be proportional to field strength. The same is true for spectroscopic analysis.
Modern low-field systems are capable to fulfill every criterion of the German MR commission (see Chap. 2), except a relative field strength homogeneity of less than 5 ppm measured peak to peak in a 40 cm sphere phantom – not because they are inhomogeneous, but because the permanent magnet opening is smaller than 40 cm. The phantom simply doesn’t fit.
The homogeneity is higher at the center of the magnetic field. Since a more flexible positioning of the body is possible in an open system, this can partly compensate for peripheral field inhomogeneity. Shoulder imaging, for example, is performed in the peripheral part of the field in a conventional closed-bore magnet system. In an open magnet, the shoulder can easily be positioned in the field center and therefore in a sufficiently homogeneous area.
5.3 T1 Relaxation
T1 and, to a smaller degree, T2 relaxation depends on field strength. With decreasing magnetic field, the T1 time (longitudinal or spin–lattice relaxation) is shortened, and T2 time (transversal or spin–spin relaxation) is prolonged.
How does this influence tissue contrast?
The most simple MR sequence is a partial saturation (sequence). Signal intensity (SI) in this sequence is given by
![$$ SI=K\times r\times \left(1- \exp \left[-TR/T1\right]\right) $$](/wp-content/uploads/2016/10/A329734_1_En_5_Chapter_Equc.gif) where K is a constant, combining the effects of flow, diffusion, perfusion, and other parameters, ρ is proton density, TR is the repetition time (time between 2 RF excitation pulses), and T1 is the time.
where K is a constant, combining the effects of flow, diffusion, perfusion, and other parameters, ρ is proton density, TR is the repetition time (time between 2 RF excitation pulses), and T1 is the time.
![$$ SI=K\times r\times \left(1- \exp \left[-TR/T1\right]\right) $$](/wp-content/uploads/2016/10/A329734_1_En_5_Chapter_Equc.gif)
This means that with shorter T1 time, signal increases. This refers to T1-weighted spin echo and gradient echo technique.
Furthermore, TR has to be less than 5 × T1 to ensure sufficient recovery of longitudinal relaxation (and hence enough spins in z-axis direction for the next 90° pulse). Therefore, with decreasing T1, TR could be shortened, increasing scan speed and partially compensating the reduced signal at lower field strength (Fischer et al. 1990).
For T2-weighted sequences, the effect of short T1 time is less important. T2 contrast increases with the echo time TE, the time interval between excitation pulse and spin echo.
Signal intensity is (SI) given by
![$$ SI=K\times r\times \left(1- \exp \left[-\left(TR-TE\right)/T1\right]\times \exp \left[-TE/T2\right]\right) $$](/wp-content/uploads/2016/10/A329734_1_En_5_Chapter_Equd.gif) where K is a constant, combining the effects of flow, diffusion, perfusion, and other parameters, ρ is proton density, TE is the echo time, TR is the repetition time, and T1 and T2 are the time.
where K is a constant, combining the effects of flow, diffusion, perfusion, and other parameters, ρ is proton density, TE is the echo time, TR is the repetition time, and T1 and T2 are the time.
![$$ SI=K\times r\times \left(1- \exp \left[-\left(TR-TE\right)/T1\right]\times \exp \left[-TE/T2\right]\right) $$](/wp-content/uploads/2016/10/A329734_1_En_5_Chapter_Equd.gif)
The contrast between body tissues is reduced, if the field strength is increased.
The same is true for the contrast between lesions and healthy tissue. Pathological changes go along with a prolongation of T1 and T2 time.
As the relaxation times converge with increasing field strength, the lesion-tissue-contrast decreases (Kaufman et al. 1989; Hayashi et al. 2004) (Fig. 5.1).
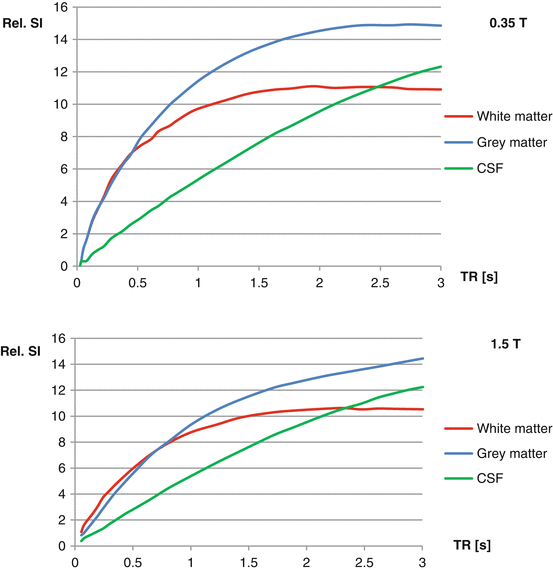

Fig. 5.1
At lower field strength, solid tissues have shorter T1 values. This gives more signal at every TR and yields better lesion-tissue-contrast
For radiologists, this is comparable to the effect of a converging mass absorption coefficient of different tissues (fat, water, bone) at increasing tube voltage in X-ray imaging.
The resulting increase in contrast-to-noise ratio can be used to partially compensate for the smaller signal-to-noise ratio in low-field systems.
In conclusion, it can be said that shorter T1 time in low-field systems improves signal intensity for T1-weighted SE, GE, and inversion recovery (STIR) sequences. Here, it partially compensates the lower signal strength.
In T2-weighted sequences, the T1-shortening effect is of less importance.
Taking all factors into consideration, there is a gain in tissue contrast at lower field strength.
5.4 Contrast-Enhanced Imaging
The effect of Gd-containing contrast agents is reduction of T1 time. If T1 is shortened in low-field imaging, this means that the contrast effect of T1 agents is reduced. While the potential of such agents to reduce T1 time is stable between 1 and 5 T, at lower field strengths, this effect becomes relevant.
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree