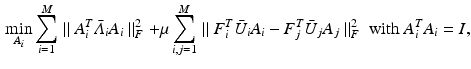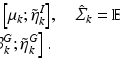Manifold Alignment of Functional Network Structures via Joint Diagonalization

consists of N voxels 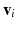$\mathbf{v}_i$ observed at T time points. The functional architecture of a brain state can be modeled as a connectivity graph G with vertices V representing the voxels, and edges E between these vertices. Let W denote the affinity matrix assigning weights to the egdes, where 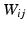$W_{ij}$ is the Pearson correlation coefficient between the time-series of vertex i and j. The spectral representation of the functional connectivity structure can be established via eigendecomposition of the normalized Laplacian matrix L, defined as 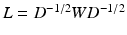$L = D^{-1/2}WD^{-1/2}$ , where D is the diagonal matrix of node degrees, i.e. 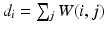$d_i = \sum _j W(i,j)$ . The normalized Laplacian is a symmetric version of the random walk matrix 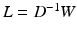$L = D^{-1}W$ , which is scaling invariant, and can be viewed as a diffusion process, where the transition probabilities for a diffusion time t between nodes can be expressed by 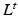. Eigendecompostion of L results in eigenvalues 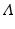$\varLambda$ and corresponding eigenvectors 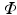$\varPhi$ , where $$$\lambda _1 = 1 > \lambda _2 > \dots > \lambda _n$$” src=”/wp-content/uploads/2016/09/A339424_1_En_36_Chapter_IEq10.gif”></SPAN>. The dataset can be represented by a diffusion map with new embedding coordinates <SPAN id=IEq11 class=InlineEquation><IMG alt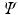=$ , where each vertex i in the original graph is represented by

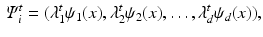
$\begin{aligned} \varPsi ^t_i =(\lambda _1^t\psi _1(x),\lambda _2^t\psi _2(x), \dots ,\lambda _d^t\psi _d(x)), \end{aligned}$

(1)

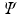for every data point x in d dimensions of the embedding space. This translates the functional organization of a brain to a functional geometry $\varPsi$ , where the functional relations of the fMRI signals are captured by the diffusion distance

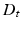[15]. The diffusion distance

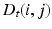is defined as the probability of traveling from node i to node j in t steps, by considering all possible paths between these two nodes. The Euclidean distance in this new embedding space approximates the diffusion distance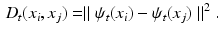

$\begin{aligned} D_t(x_i,x_j) = \parallel \psi _t(x_i) - \psi _t(x_j) \parallel ^2. \end{aligned}$

(2)

Thus, the functional relationship between voxels of a brain is translated to Euclidean distances in a new embedding space, capturing the functional geometry of the dataset. This uncouples function from anatomy, and is the basis for functional registration of corresponding functional structures across individuals [15].

2.2 Initial Correspondence Estimates Across Individuals

We aim at aligning functionally equivalent areas across individuals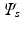. Assuming that for a majority of functional areas the spatial difference is small we use spatial correspondence for initialization. We perform an initial two-step manifold alignment following the initialization procedure in [15]. First, we align brain morphology to a common template [8]. Then, we orthonormally align individual embedding maps representing each subject based on correspondence defined by spatial position in the common template. For every subject specific embedding $\varPsi _{s}$ and template embedding 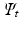$\varPsi _{t}$ , an orthonormal transformation matrix 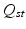$Q_{st}$ is calculated, accounting for rotations, sign flips and reordering of the spectral dimensions. 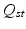$Q_{st}$ is defined as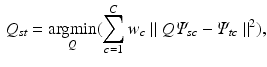

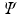$\begin{aligned} Q_{st} = \mathop {\hbox {argmin}}\limits _Q ( \sum ^{C}_{c=1} w_c \parallel Q\varPsi _{sc} - \varPsi _{tc} \parallel ^2 ), \end{aligned}$

(3)

where $\varPsi$ are the embeddings of s and t and w is the Euclidean distance between a pair c of corresponding voxels. After this initial alignment of embeddings, we perform nonrigid point cloud registration to refine the alignment and close potential gaps between the embedded sampling point distributions by Coherent Point Drift [19].

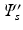While preserving the functional relationship between brain regions, diffusion maps typically encode a distinct functionally coherent cluster of brain regions along a specific dimension, far from the origin in the leading dimensions of the embedding space. 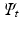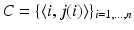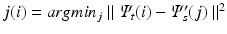We use this property to obtain initial pairwise point-to-point correspondence estimates between two orthonormally aligned diffusion maps $\varPsi '_s$ and $\varPsi _t$ , resulting in n correspondence pairs $C = \{ \langle i,j(i)\rangle \}_{i=1,\dots ,n}$ with $j(i) = argmin_j \parallel \varPsi _t(i) - \varPsi '_s (j)\parallel ^2$ . For each pair of embeddings, a subset of q correspondence pairs C is selected based on their distance from the origin and used as initial coupling for joint diagonalization, described in the following section. Note that the purpose of this initial alignment is only to determine a subset of initial correspondence esimates. Sub-sequent joint diagonalization is based on the individual Laplacians and the correspondence pairs.

2.3 Joint Diagonalization

Joint diagonalization simultaneously finds the common eigenbases of the Laplacians of multiple datasets [2, 6, 13]. In theory, if multiple datasets share similar intrinsic structures, their Laplacians have similar eigenbases with variations in rotations, coefficient sign or ordering of spectral components. Joint diagonalization results in coupled eigenbases, which make the eigenbases of each individual dataset consistent. The basic joint diagonalization problem with full coupling can be formulated as an optimization problem of minimizing off-diagonal elements:

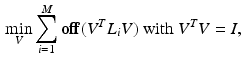
$\begin{aligned} \mathop {\hbox {min}}\limits _V \sum _{i=1}^{M} \mathbf{off}(V^T L_i V) \text { with } V^TV=I, \end{aligned}$

(4)

where M is the number of different datasets, V is their common eigenbases,

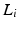are the dataset specific Laplacians. The off-diagonal penalty 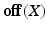$\mathbf{off}(X)$ is typically defined as the sum of squared off diagonal elements 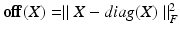$\mathbf{off}(X) = \parallel X - diag(X) \parallel ^2_F$ . This problem can be solved with the generalized Jacobi method (JADE method) [2]. It assumes full coupling with an equal amount of samples for every dataset, i.e. every sampling point in a dataset has a corresponding point in all other datasets. In our case we cannot assume identical numbers of sampling points or complete given correspondences between datasets. Instead we only use a sub-set of paired vertices to guide the joint diagonalization.

Coupled diagonalization allows to overcome these limitations [6, 13]. Only a subset of sparse point-wise correspondences is used to establish a coupling relation F.

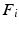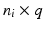is a $n_i \times q$ coupling matrix, where

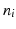is the number of data points and q is the number of correspondences. Based on this sparse subset, eigenbases

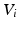are established, such that

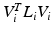is approximately diagonal and the eigenbases correspond for corresponding samples 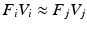$F_iV_i \approx F_jV_j$ . This results in multiple dataset specific eigenbases, contrary to the original joint diagonalization approach [2].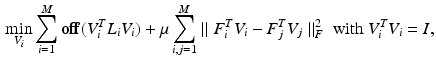

To incorporate the coupling between datasets, the formulation in Eq. 4 can be rewritten as

$\begin{aligned} \mathop {\hbox {min}}\limits _{V_i} \sum _{i=1}^{M} \mathbf{off}(V_i^T L_i V_i) + \mu \sum _{i,j=1}^{M} \parallel F_i^TV_i - F_j^TV_j \parallel ^2_F \text { with } V_i^TV_i=I, \end{aligned}$

(5)

where

are the dataset specific eigenbases,

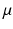the data specific Laplacians and $\mu$ is a coupling weight [6]. The sparse coupling between two datasets i and j is defined by corresponding points

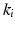and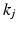

and encoded as

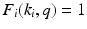and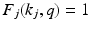

, with zeros elsewhere in the 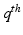$q^{th}$ column. However, the coupling is not restricted to such point-wise coupling, and can contain any correspondence weighting. We use the leading k dimensions of the embedding, since they hold the majority of information. This reduces the computational complexity to an optimization problem with

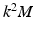variables, instead of 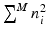$\sum ^M n_i^2$ variables for full eigenbases. Then, the formulation in Eq. 5 can be rewritten as

$\begin{aligned} \mathop {\hbox {min}}\limits _{A_i} \sum _{i=1}^{M} \parallel A_i^T \bar{\varLambda }_i A_i \parallel ^2_F + \mu \sum _{i,j=1}^{M} \parallel F_i^T\bar{U}_iA_i - F_j^T\bar{U}_jA_j \parallel ^2_F \text { with } A_i^TA_i=I, \end{aligned}$