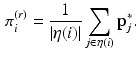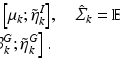(e.g. a time series of N images with D pixels each) lies on a manifold  which can be described by much fewer dimensions. Manifold learning techniques map each point
which can be described by much fewer dimensions. Manifold learning techniques map each point 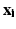 in the high-dimensional dataset to a low-dimensional point
in the high-dimensional dataset to a low-dimensional point 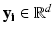 , where
, where 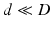 , while preserving the local neighbourhood structure of the high-dimensional points on
, while preserving the local neighbourhood structure of the high-dimensional points on 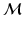 . The low-dimensional points form a new low-dimensional dataset
. The low-dimensional points form a new low-dimensional dataset 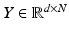 .
.
LLE models the locality of the high-dimensional space by first constructing a graph of the data points and then calculating the weights which reconstruct each high-dimensional point as a linear combination of its k-nearest neighbours. The optimal contribution of each point j to the reconstruction of i is given by the weights 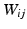 and can be calculated as described in [11]. The embedding preserving this structure is given by the Y minimising the cost function
and can be calculated as described in [11]. The embedding preserving this structure is given by the Y minimising the cost function
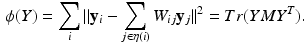
Here, 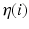 is the neighbourhood of each point i and
is the neighbourhood of each point i and 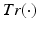 is the trace operator. This optimisation problem can be solved by calculating the eigendecomposition of the centred reconstruction weight matrix
is the trace operator. This optimisation problem can be solved by calculating the eigendecomposition of the centred reconstruction weight matrix 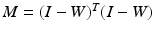 . The embedding Y is given by the eigenvectors corresponding to the second smallest to
. The embedding Y is given by the eigenvectors corresponding to the second smallest to 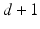 smallest eigenvalues of M [11].
smallest eigenvalues of M [11].
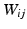 and can be calculated as described in [11]. The embedding preserving this structure is given by the Y minimising the cost function
and can be calculated as described in [11]. The embedding preserving this structure is given by the Y minimising the cost function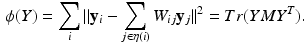
(1)
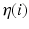 is the neighbourhood of each point i and
is the neighbourhood of each point i and 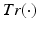 is the trace operator. This optimisation problem can be solved by calculating the eigendecomposition of the centred reconstruction weight matrix
is the trace operator. This optimisation problem can be solved by calculating the eigendecomposition of the centred reconstruction weight matrix 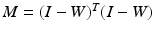 . The embedding Y is given by the eigenvectors corresponding to the second smallest to
. The embedding Y is given by the eigenvectors corresponding to the second smallest to 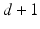 smallest eigenvalues of M [11].
smallest eigenvalues of M [11].It is well known that when manifold learning is applied to time series of medical images under free breathing, the low dimensional coordinates 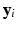 contain useful information about the motion. In particular, when reducing the data to a one dimensional space (
contain useful information about the motion. In particular, when reducing the data to a one dimensional space (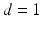 ) the embedding strongly correlates with a respiratory navigator obtained by traditional means [14]. Baumgartner et al. [1] showed that embeddings in higher dimensions can give additional information on respiratory variation such as hysteresis or respiratory drift over time.
) the embedding strongly correlates with a respiratory navigator obtained by traditional means [14]. Baumgartner et al. [1] showed that embeddings in higher dimensions can give additional information on respiratory variation such as hysteresis or respiratory drift over time.
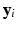 contain useful information about the motion. In particular, when reducing the data to a one dimensional space (
contain useful information about the motion. In particular, when reducing the data to a one dimensional space (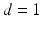 ) the embedding strongly correlates with a respiratory navigator obtained by traditional means [14]. Baumgartner et al. [1] showed that embeddings in higher dimensions can give additional information on respiratory variation such as hysteresis or respiratory drift over time.
) the embedding strongly correlates with a respiratory navigator obtained by traditional means [14]. Baumgartner et al. [1] showed that embeddings in higher dimensions can give additional information on respiratory variation such as hysteresis or respiratory drift over time.2.2 Manifold Alignment by Simultaneous Embedding
Medical image datasets which have the same source of motion often lie on similar low-dimensional manifolds. Within the context of this work the different datasets are free breathing images acquired from different views, i.e. different slice positions (MR) or different probe locations (US). Bringing the manifolds into a globally consistent coordinate system allows the matching of images at similar respiratory positions between the different views.
Unfortunately, the embeddings obtained using manifold learning techniques are arbitrary with respect to the sign of the eigenvectors (i.e. arbitrary flipping). In addition, the manifolds obtained from different datasets often feature small but significant differences in shape such as small rotations or scaling differences, which further complicate their alignment. In order to relate the respiratory positions of L different datasets ![$$X_1,\dots , X_L : X_{\ell } = [\mathbf {x^{(\ell )}_1},\dots ,\mathbf {x^{(\ell )}_N} ]$$](/wp-content/uploads/2016/09/A339424_1_En_28_Chapter_IEq15.gif) (e.g. free breathing images obtained from L different views) in the low-dimensional space, first the underlying manifold embeddings
(e.g. free breathing images obtained from L different views) in the low-dimensional space, first the underlying manifold embeddings 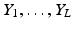 must be aligned.
must be aligned.
![$$X_1,\dots , X_L : X_{\ell } = [\mathbf {x^{(\ell )}_1},\dots ,\mathbf {x^{(\ell )}_N} ]$$](/wp-content/uploads/2016/09/A339424_1_En_28_Chapter_IEq15.gif) (e.g. free breathing images obtained from L different views) in the low-dimensional space, first the underlying manifold embeddings
(e.g. free breathing images obtained from L different views) in the low-dimensional space, first the underlying manifold embeddings 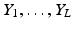 must be aligned.
must be aligned.Our solution to the alignment problem is to formulate a joint cost function and then compute an embedding for all datasets simultaneously in one embedding step. This approach is the general case for L datasets of the formulation proposed in [1] for two datasets. However, to the best of our knowledge, LLE has not been extended to embed ![$$L>2$$” src=”/wp-content/uploads/2016/09/A339424_1_En_28_Chapter_IEq17.gif”></SPAN> datasets simultaneously. This can be done by augmenting the cost function from Eq. (<SPAN class=InternalRef><A href=]() 1) as follows:
1) as follows:
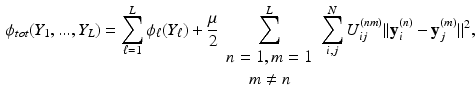
where 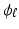 is given by Eq. (1). The second term of Eq. (2) is the cost function relating all datasets to each other.
is given by Eq. (1). The second term of Eq. (2) is the cost function relating all datasets to each other. 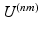 is a similarity kernel relating points from dataset n to dataset m. Large values in
is a similarity kernel relating points from dataset n to dataset m. Large values in 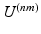 force corresponding points to be close together in the resulting embedding.
force corresponding points to be close together in the resulting embedding. 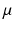 is a weighting parameter which governs the influence of the inter-dataset terms.
is a weighting parameter which governs the influence of the inter-dataset terms. 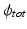 can be rewritten in matrix form as
can be rewritten in matrix form as 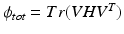 , where V is a
, where V is a 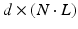 matrix containing the concatenated embeddings,
matrix containing the concatenated embeddings, ![$$V = [Y_1,\dots ,Y_L]$$](/wp-content/uploads/2016/09/A339424_1_En_28_Chapter_IEq25.gif) , and
, and
![$$\begin{aligned} H = \left[ \begin{array}{cccc} M^{(1)} + \mu {\sum }_p D^{(1p)} &{} -\mu U^{(12)} &{} \ldots &{} -\mu U^{(1L)} \\ -\mu U^{(21)} &{} M^{(2)} + \mu {\sum }_p D^{(2p)} &{} \ldots &{} -\mu U^{(2L)} \\ \vdots &{} \ &{} \ddots &{} \vdots \\ -\mu U^{(L1)} &{} -\mu U^{(L2)} &{} \ldots &{} M^{(L)} + \mu {\sum }_p D^{(Lp)} \end{array} \right] \end{aligned}$$](/wp-content/uploads/2016/09/A339424_1_En_28_Chapter_Equ3.gif)
Here, the diagonal degree matrices 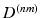 are given by
are given by 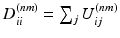 . Under the scaling constraint
. Under the scaling constraint 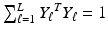 , the embeddings V are given by the second smallest to
, the embeddings V are given by the second smallest to  smallest eigenvectors of H.
smallest eigenvectors of H.
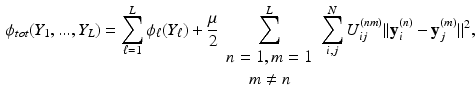
(2)
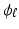 is given by Eq. (1). The second term of Eq. (2) is the cost function relating all datasets to each other.
is given by Eq. (1). The second term of Eq. (2) is the cost function relating all datasets to each other. 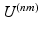 is a similarity kernel relating points from dataset n to dataset m. Large values in
is a similarity kernel relating points from dataset n to dataset m. Large values in 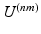 force corresponding points to be close together in the resulting embedding.
force corresponding points to be close together in the resulting embedding. 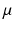 is a weighting parameter which governs the influence of the inter-dataset terms.
is a weighting parameter which governs the influence of the inter-dataset terms. 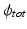 can be rewritten in matrix form as
can be rewritten in matrix form as 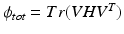 , where V is a
, where V is a 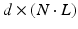 matrix containing the concatenated embeddings,
matrix containing the concatenated embeddings, ![$$V = [Y_1,\dots ,Y_L]$$](/wp-content/uploads/2016/09/A339424_1_En_28_Chapter_IEq25.gif) , and
, and![$$\begin{aligned} H = \left[ \begin{array}{cccc} M^{(1)} + \mu {\sum }_p D^{(1p)} &{} -\mu U^{(12)} &{} \ldots &{} -\mu U^{(1L)} \\ -\mu U^{(21)} &{} M^{(2)} + \mu {\sum }_p D^{(2p)} &{} \ldots &{} -\mu U^{(2L)} \\ \vdots &{} \ &{} \ddots &{} \vdots \\ -\mu U^{(L1)} &{} -\mu U^{(L2)} &{} \ldots &{} M^{(L)} + \mu {\sum }_p D^{(Lp)} \end{array} \right] \end{aligned}$$](/wp-content/uploads/2016/09/A339424_1_En_28_Chapter_Equ3.gif)
(3)
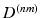 are given by
are given by 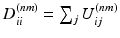 . Under the scaling constraint
. Under the scaling constraint 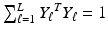 , the embeddings V are given by the second smallest to
, the embeddings V are given by the second smallest to 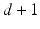 smallest eigenvectors of H.
smallest eigenvectors of H.2.3 Similarity Without Correspondences
All previous work on simultaneous embeddings has either used known prior correspondences to define the similarity kernels 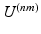 [5], or has used similarity measures between the high-dimensional data to define it [1, 8]. The notable exception is [15] which we discussed in the introduction. For many applications, however, it is desirable to simultaneously embed medical image datasets which are not comparable in image space and for which prior correspondences are not easily obtainable. This problem is effectively one of finding a suitable inter-dataset similarity kernel
[5], or has used similarity measures between the high-dimensional data to define it [1, 8]. The notable exception is [15] which we discussed in the introduction. For many applications, however, it is desirable to simultaneously embed medical image datasets which are not comparable in image space and for which prior correspondences are not easily obtainable. This problem is effectively one of finding a suitable inter-dataset similarity kernel 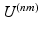 that connects datasets
that connects datasets 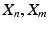 but which is not based on comparisons between datasets in the high-dimensional space.
but which is not based on comparisons between datasets in the high-dimensional space.
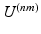 [5], or has used similarity measures between the high-dimensional data to define it [1, 8]. The notable exception is [15] which we discussed in the introduction. For many applications, however, it is desirable to simultaneously embed medical image datasets which are not comparable in image space and for which prior correspondences are not easily obtainable. This problem is effectively one of finding a suitable inter-dataset similarity kernel
[5], or has used similarity measures between the high-dimensional data to define it [1, 8]. The notable exception is [15] which we discussed in the introduction. For many applications, however, it is desirable to simultaneously embed medical image datasets which are not comparable in image space and for which prior correspondences are not easily obtainable. This problem is effectively one of finding a suitable inter-dataset similarity kernel 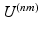 that connects datasets
that connects datasets 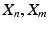 but which is not based on comparisons between datasets in the high-dimensional space.
but which is not based on comparisons between datasets in the high-dimensional space.In this paper we propose a novel, robust method for deriving an inter-dataset similarity kernel. Instead of directly comparing the data from different datasets in the high-dimensional space we first analyse the internal graph structure of each dataset and derive a characteristic feature vector for each node. In the next step we compare these feature vectors across datasets. This approach is an extension of the method proposed in [3] for graph matching.
Deriving a Characteristic Feature Vector for Each Node. For each dataset X we form a fully connected, weighted graph 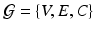 , connecting each node in V to every other with edges E. The edge weights
, connecting each node in V to every other with edges E. The edge weights 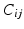 connecting node
connecting node 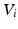 to
to 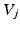 are given by a Gaussian kernel
are given by a Gaussian kernel
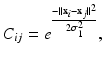 where
where 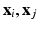 are the high-dimensional data points of X, and
are the high-dimensional data points of X, and 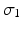 is a shape parameter. Note that
is a shape parameter. Note that 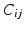 is formed by intra-dataset comparisons only.
is formed by intra-dataset comparisons only.
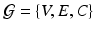 , connecting each node in V to every other with edges E. The edge weights
, connecting each node in V to every other with edges E. The edge weights 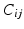 connecting node
connecting node 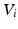 to
to 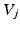 are given by a Gaussian kernel
are given by a Gaussian kernel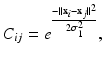
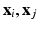 are the high-dimensional data points of X, and
are the high-dimensional data points of X, and 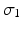 is a shape parameter. Note that
is a shape parameter. Note that 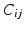 is formed by intra-dataset comparisons only.
is formed by intra-dataset comparisons only.As noted in [3], the steady-state distribution of a (lazy) random walk, i.e. the probability 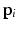 of ending up at a particular node
of ending up at a particular node 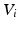 after
after 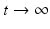 time steps, can provide information about each node’s location in the graph. In a lazy random walk the walker remains at their current node
time steps, can provide information about each node’s location in the graph. In a lazy random walk the walker remains at their current node 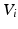 with probability 0.5 at each time step and walks to a random neighbour
with probability 0.5 at each time step and walks to a random neighbour 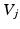 with a probability given by the edge weights
with a probability given by the edge weights 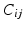 the other half of the time. The state of the random walk in a weighted graph after
the other half of the time. The state of the random walk in a weighted graph after 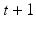 time steps is given by
time steps is given by 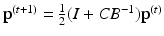 , where B is the diagonal degree matrix given by
, where B is the diagonal degree matrix given by 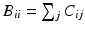 . The steady state distribution is stationary and is given by
. The steady state distribution is stationary and is given by
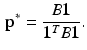
In [3], 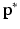 was used to perform graph matching. In our experiments,
was used to perform graph matching. In our experiments, 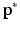 alone was not sufficiently robust to align our datasets. Therefore, to increase the robustness of this measure we propose to additionally analyse the neighbourhood of each node. For each
alone was not sufficiently robust to align our datasets. Therefore, to increase the robustness of this measure we propose to additionally analyse the neighbourhood of each node. For each 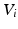 we select the r-nearest neighbours and evaluate their
we select the r-nearest neighbours and evaluate their 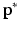 as well, by forming an average over the neighbourhood:
as well, by forming an average over the neighbourhood:
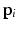 of ending up at a particular node
of ending up at a particular node 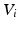 after
after 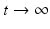 time steps, can provide information about each node’s location in the graph. In a lazy random walk the walker remains at their current node
time steps, can provide information about each node’s location in the graph. In a lazy random walk the walker remains at their current node 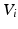 with probability 0.5 at each time step and walks to a random neighbour
with probability 0.5 at each time step and walks to a random neighbour 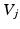 with a probability given by the edge weights
with a probability given by the edge weights 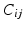 the other half of the time. The state of the random walk in a weighted graph after
the other half of the time. The state of the random walk in a weighted graph after 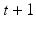 time steps is given by
time steps is given by 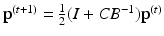 , where B is the diagonal degree matrix given by
, where B is the diagonal degree matrix given by 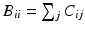 . The steady state distribution is stationary and is given by
. The steady state distribution is stationary and is given by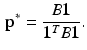
(4)
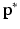 was used to perform graph matching. In our experiments,
was used to perform graph matching. In our experiments, 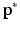 alone was not sufficiently robust to align our datasets. Therefore, to increase the robustness of this measure we propose to additionally analyse the neighbourhood of each node. For each
alone was not sufficiently robust to align our datasets. Therefore, to increase the robustness of this measure we propose to additionally analyse the neighbourhood of each node. For each 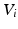 we select the r-nearest neighbours and evaluate their
we select the r-nearest neighbours and evaluate their 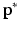 as well, by forming an average over the neighbourhood:
as well, by forming an average over the neighbourhood: