and Dorin Comaniciu1
(1)
Imaging and Computer Vision, Siemens Corporate Technology, Princeton, NJ, USA
Abstract
This chapter presents an efficient 3D learning-based object detection method, called Marginal Space Learning (MSL). The idea of MSL is to avoid learning in the full similarity transformation space by incrementally learning classifiers in marginal spaces of lower dimensions. The estimation of an object’s pose is split into three problems: position estimation, position-orientation estimation, and position-orientation-scale estimation. This incremental learning approach contributes to a highly efficient object detection paradigm. In addition, we introduce the steerable features, as a mechanism to search the orientation space, thus avoiding expensive volume/image rotations. The main idea is to sample points from a given volume under a sampling pattern that embeds the position, orientation, and scale information of a pose hypothesis. Each sample point is associated with a set of local features such as local intensity and gradient. The efficiency of steerable features comes from the fact that much fewer points (defined by the sampling pattern) are needed for manipulation, in comparison to the whole volume.
2.1 Introduction
Automatic detection of an anatomical structure (object) in medical images is a prerequisite for subsequent tasks such as recognition, segmentation, measurement, or motion tracking, and therefore has numerous applications. The goal of the detection is to estimate the position, orientation, and size of the target anatomical structure. The pose parameters can be represented as an oriented bounding box (to distinguish from an axis-aligned bounding box ).
Recently, discriminative learning based approaches have been proved to be efficient and robust to detect 2D objects [14, 31]. In these methods, object detection is formulated as a classification problem: whether an image window contains the target object or not [31]. During object detection, the pose parameter space is quantized into a large set of discrete hypotheses and each hypothesis is tested by a trained classifier to get a detection score. The hypotheses with the highest score are taken as the detection results. Exhaustive search for the best hypothesis makes the system robust under local optima . This search strategy is quite different from other parameter estimation approaches, such as deformable models , where an initial estimate is adjusted using the gradient descent techniques to optimize a predefined objective function.
There are two challenges to extend learning based object detection approaches to 3D. First, the number of hypotheses increases exponentially with respect to the dimensionality of the parameter space. Although the dimensionality of the image space only increases by one from 2D to 3D, the dimensionality of the pose parameter space increases from 5 to 9. For 2D object detection, there are five unknown parameters to be estimated or searched for from an input image, namely, translation in two directions, one rotation angle, and two scales. For 3D object detection, there are nine degrees of freedom for the anisotropic similarity transformation , namely three translation parameters, three rotation angles, and three scales. Note that the ordinary similarity transformation defines only isotropic scaling, corresponding to one scale parameter. However, to better cope with nonrigid deformations of the target object, we use anisotropic scales. The number of hypotheses is an exponential function of the dimensionality of the pose parameter space. If each dimension is quantized to n discrete values, the number of hypotheses is n 9. For a very coarse estimation with n = 10, n 9 = 1,000,000,000 for 3D instead of n 5 = 100,000 for 2D. As a result, the computational demands for the 3D case present a challenge to the current desktop computers, to provide the testing results in a reasonable time. Even a five dimensional pose parameter space for a 2D object is already too large to achieve real-time performance. Note that for the 2D face detection example in [31], they only searched a three dimensional pose parameter space, two dimensions for position and one dimension for isotropic scaling , by constraining the face in an up-straight front view with a fixed aspect ratio.
The second challenge of extending the learning based object detection to 3D is that we need efficient features to search the orientation space . To perform a classification to an orientation hypothesis , the image features should be a function of the orientation hypothesis. Since we want to explicitly estimate the orientation of an object, rotation invariant features cannot be applied. There are two ways to embed the orientation information into image features, rotating either the feature template or the volume. Haar wavelet features can be efficiently computed under translation and scaling using the integral images [24, 31], but no efficient ways are available to rotate the Haar wavelet features. For 2D object detection, there is only one degree of freedom in rotation. It is possible to discretize orientation into a small number of categories, e.g., 10∘ of incremental rotation in [0, 360∘), resulting in 36 orientations. The input image is rotated accordingly for each orientation category to generate a set of rotated images. A detector is trained under one fixed orientation and is applied to all the rotated images to detect an object with different orientations [8]. However, a 3D volume contains much more data; therefore, it is very time consuming to rotate the volume. The computation time to rotate a volume with 512 × 512 × 512 voxels is equivalent to rotate 512 images each with 512 × 512 pixels. Furthermore, there are three degrees of freedom in 3D rotations . To cover the full orientation space with a sampling resolution of 9. 72∘, we need 7416 discrete orientation hypotheses [18]. Since volume rotation is time consuming, it is impractical to perform thousands of volume rotations for orientation estimation .
This chapter presents solutions to the two challenges discussed above. First, it introduces an efficient 3D learning-based object detection method, called Marginal Space Learning (MSL). The idea of MSL is to avoid learning in the full similarity transformation space by incrementally learning classifiers in marginal spaces of lower dimensions. The estimation of an object’s pose is split into three problems: position estimation , position-orientation estimation , and position-orientation-scale estimation . This incremental learning approach contributes to a highly efficient object detection paradigm. Second, we introduce the steerable features , as a mechanism to search the orientation space, thus avoiding expensive volume/image rotations. The idea is to sample points (voxels) from a given volume under a sampling pattern that embeds the position, orientation, and scale information of a pose hypothesis. Each sample point is associated with a set of local features such as local intensity and gradient. The efficiency of steerable features comes from the fact that much fewer points (defined by the sampling pattern) are needed for manipulation, in comparison to the whole volume.
The remainder of this chapter is organized as follows. In Sect. 2.2, we present the whole MSL workflow, including the derivation of the pose parameter ground truth from a training set with annotated meshes, training of each individual pose parameter estimator, and aggregation of multiple pose candidates to achieve a consolidated estimate of the object. We then discuss implementation details, introducing 3D image features in Sect. 2.3 and the Probabilistic Boosting-Tree (PBT) classifier in Sect. 2.4. In Sect. 2.5, we use automatic 3D heart chamber detection in CT volumes as an example to demonstrate the efficiency and robustness of MSL. In Sect. 2.6, we extend the MSL principle to directly estimate nonrigid deformation parameters to further improve the shape initialization accuracy for nonrigid object segmentation. In Sect. 2.7, we provide theoretical justifications of MSL and link it to the shortest path computation in graph search. The MSL is shown to be an efficient breadth-first beam search in the posterior probability of the pose parameter space. This chapter concludes with Sect. 2.8.
2.2 3D Object Detection Using Marginal Space Learning
For an in-depth understanding of this section, we refer the reader to earlier learning based object detection publications [14, 29, 31].
2.2.1 Derivation of Object Pose Ground Truth From Mesh
To train object detection classifiers, we need a set of 3D volumes, called the training set. The volumes in the training set are typically converted to a low isotropic resolution (e.g., 3 mm). For each volume, we need a nine dimensional vector of the ground truth about the position, orientation, and size of the target object in the volume. These nine pose parameters can be visually represented as a bounding box of the object. In some applications, the pose parameters are readily available from the annotation of the image data. This is especially common for 2D object detection since it is easy to draw a bounding box of the target object. However, drawing a 3D bounding box aligned with the orientation of the 3D object is not trivial. It is more convenient to annotate a few landmarks of the object and derive a box from the landmarks. Alternatively, since in many applications, the accurate object segmentation is the ultimate goal, a 3D surface mesh is annotated by experts for each volume in the training set, either manually or semi-automatically. In the following, we present an ad-hoc method to derive the 3D pose parameters/bounding box of a surface mesh. This is an intuitive solution, but by no means optimal. In Chap. 6, we present a more theoretically founded solution to derive optimal nine pose parameters from a set of 3D meshes to minimize the mesh initialization error after pose estimation.
The object orientation cannot be easily derived from a 3D mesh. Different methods are often demanded to define the orientation of different target objects. Many anatomies have an intrinsic, well-accepted orientation definition. For example, the orientation of the heart chambers , defined by the long axis and short axis , is documented in detail by the echocardiography community [17]. In the heart chamber segmentation application [33, 34], we use the long axis of a chamber as the z axis. The perpendicular direction from a predefined anchor point to the long axis defines axis x. For different chambers, we have freedom to select the anchor point, as long as it is consistent. For example, for the left ventricle , we can use the aortic valve center as the anchor point. The third axis y is the cross-product of axes z and x. A 3 × 3 rotation matrix R is determined using the x, y, and z axis as the first, second, and last column of R, respectively. An orientation hypothesis is represented as three Euler angles , ψ t , ϕ t , and θ t , which can be derived from the rotation matrix R using the following relationship
![$$\displaystyle{ \mathbf{R} = \left [\begin{array}{ccccc} \cos \psi \cos \phi -\cos \theta \sin \phi \sin \psi && \cos \psi \sin \phi +\cos \theta \cos \phi \sin \psi &&\sin \psi \sin \theta \\ -\sin \psi \cos \phi -\cos \theta \sin \phi \cos \psi & & -\sin \psi \sin \phi +\cos \theta \cos \phi \cos \psi & &\cos \psi \sin \theta \\ \sin \theta \sin \phi && -\sin \theta \cos \phi &&\cos \theta \\ \end{array} \right ]. }$$](/wp-content/uploads/2016/08/A314110_1_En_2_Chapter_Equ1.gif)
(2.1)
For object segmentation, we also need to calculate the mean shape from the training set so that after object pose estimation we can align the mean shape to get an initial estimate of the true shape. For a target object, using the above bounding box based method, we calculate its position (T = [X, Y, Z]′), orientation (represented as a rotation matrix R), and anisotropic scaling (S = [S x , S y , S z ]′). We then transform each point from the world coordinate system , M world , to the object-oriented coordinate system , m object , and calculate the average over the whole training set to get a mean shape. Here, we assume that the training shapes have intrinsic mesh point correspondence , namely, each mesh has the same number of points and the same point index in different meshes corresponds to the same anatomy. The transformation between M world and m object is
![$$\displaystyle{ \mathbf{M}_{world} = \mathbf{R}\left [\begin{array}{ccc} S_{x}& 0 & 0 \\ 0 &S_{y}& 0 \\ 0 & 0 &S_{z}\\ \end{array} \right ]\mathbf{m}_{object}+\mathbf{T}. }$$](/wp-content/uploads/2016/08/A314110_1_En_2_Chapter_Equ2.gif)
Reversing the transformation, we can calculate the position in the object-oriented coordinate system as
![$$\displaystyle{ \mathbf{m}_{object} = \left [\begin{array}{ccc} \frac{1} {S_{x}} & 0 & 0 \\ 0 & \frac{1} {S_{y}} & 0 \\ 0 & 0 & \frac{1} {S_{z}}\\ \end{array} \right ]{\mathbf{R}}^{-1}\left (\mathbf{M}_{ world} -\mathbf{T}\right ). }$$](/wp-content/uploads/2016/08/A314110_1_En_2_Chapter_Equ3.gif)
The mean shape is the average over the whole training set
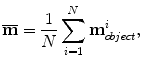
where N is the number of training samples.
![$$\displaystyle{ \mathbf{M}_{world} = \mathbf{R}\left [\begin{array}{ccc} S_{x}& 0 & 0 \\ 0 &S_{y}& 0 \\ 0 & 0 &S_{z}\\ \end{array} \right ]\mathbf{m}_{object}+\mathbf{T}. }$$](/wp-content/uploads/2016/08/A314110_1_En_2_Chapter_Equ2.gif)
(2.2)
![$$\displaystyle{ \mathbf{m}_{object} = \left [\begin{array}{ccc} \frac{1} {S_{x}} & 0 & 0 \\ 0 & \frac{1} {S_{y}} & 0 \\ 0 & 0 & \frac{1} {S_{z}}\\ \end{array} \right ]{\mathbf{R}}^{-1}\left (\mathbf{M}_{ world} -\mathbf{T}\right ). }$$](/wp-content/uploads/2016/08/A314110_1_En_2_Chapter_Equ3.gif)
(2.3)
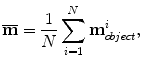
(2.4)
2.2.2 Principle of Marginal Space Learning
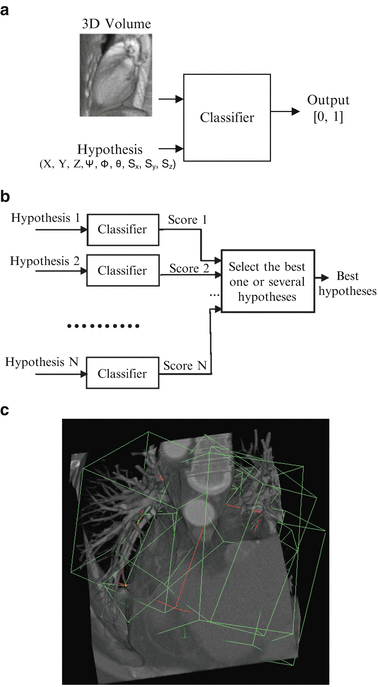
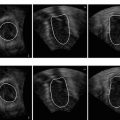
Fig. 2.1
The basic idea of a machine learning based 3D object detection. (a) A trained classifier assigns a score to a pose hypothesis. (b) The pose parameter space is quantized into a large number of discrete hypotheses and the classifier is used to select the best hypotheses through exhaustive search. (c) A few pose hypotheses of the left ventricle (represented as boxes) embedded in a CT volume. ©2008 IEEE. Reprinted, with permission, from Zheng, Y., Barbu, A., Georgescu, B., Scheuering, M., Comaniciu, D.: Four-chamber heart modeling and automatic segmentation for 3D cardiac CT volumes using marginal space learning and steerable features. IEEE Trans. Medical Imaging 27(11), 1668–1681 (2008)
Figure 2.1 shows the basic idea of machine learning based 3D object detection. First, we train a classifier, which assigns a score in the range [0, 1] to each input hypothesis about the object pose. We then quantize the full pose parameter space into a large number of hypotheses. Depending on the quantization resolution, the number of hypotheses can easily reach an order over 1 billion. Each hypothesis is tested with the classifier to get a score. Based on the classification scores, we select the best one or several hypotheses. We may need to aggregate multiple best hypotheses into a final single detection result. Unlike the gradient based search in deformable models or Active Appearance Models (AAM) [4], the classifier in this framework acts as a black box without an explicit closed-form objective function.
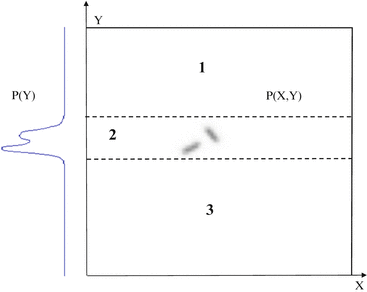
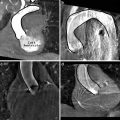
Fig. 2.2
Marginal space learning to search the peaks of the joint distribution p(x, y). A classifier trained on a marginal distribution p(y) can quickly eliminate a large portion (regions 1 and 3) of the search space. Another classifier is then trained on a restricted space (region 2) for the joint distribution p(x, y). ©2008 IEEE. Reprinted, with permission, from Zheng, Y., Barbu, A., Georgescu, B., Scheuering, M., Comaniciu, D.: Four-chamber heart modeling and automatic segmentation for 3D cardiac CT volumes using marginal space learning and steerable features. IEEE Trans. Medical Imaging 27(11), 1668–1681 (2008)
As we discussed, one drawback of the learning based approach is that the number of hypotheses increases exponentially with respect to the dimensionality of the parameter space. Nevertheless, in many applications, the posterior distribution is clustered in a small region in the high dimensional parameter space. Therefore, the uniform and exhaustive search is not necessary and wastes the computational power.
The MSL is an efficient method to partition such parameter space, by gradually increasing the dimensionality of the search space. Let Ω be the space where the solution to the given problem exists and let P Ω be the true probability distribution that needs to be learned. The learning and computation are performed in a sequence of marginal spaces
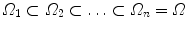
such that Ω 1 is a low dimensional space (e.g., three-dimensional translation instead of nine-dimensional similarity transformation), and for each k, 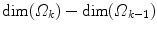 is small. A search in the marginal space Ω 1 using the learned probability model finds a subspace Π 1 ⊂ Ω 1 containing the most probable values and discards the rest of the space. The restricted marginal space Π 1 is then extended to Π 1 e = Π 1 × X 1 ⊂ Ω 2. Another stage of learning and testing is performed on Π 1 e obtaining a restricted marginal space Π 2 ⊂ Ω 2 and the procedure is repeated until the full space Ω is reached. At each step, the restricted space Π k is one or two orders of magnitude smaller than Π k−1 × X k . This results in a very efficient algorithm with minimal loss in performance.
is small. A search in the marginal space Ω 1 using the learned probability model finds a subspace Π 1 ⊂ Ω 1 containing the most probable values and discards the rest of the space. The restricted marginal space Π 1 is then extended to Π 1 e = Π 1 × X 1 ⊂ Ω 2. Another stage of learning and testing is performed on Π 1 e obtaining a restricted marginal space Π 2 ⊂ Ω 2 and the procedure is repeated until the full space Ω is reached. At each step, the restricted space Π k is one or two orders of magnitude smaller than Π k−1 × X k . This results in a very efficient algorithm with minimal loss in performance.
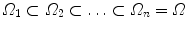
(2.5)
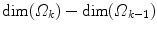 is small. A search in the marginal space Ω 1 using the learned probability model finds a subspace Π 1 ⊂ Ω 1 containing the most probable values and discards the rest of the space. The restricted marginal space Π 1 is then extended to Π 1 e = Π 1 × X 1 ⊂ Ω 2. Another stage of learning and testing is performed on Π 1 e obtaining a restricted marginal space Π 2 ⊂ Ω 2 and the procedure is repeated until the full space Ω is reached. At each step, the restricted space Π k is one or two orders of magnitude smaller than Π k−1 × X k . This results in a very efficient algorithm with minimal loss in performance.
is small. A search in the marginal space Ω 1 using the learned probability model finds a subspace Π 1 ⊂ Ω 1 containing the most probable values and discards the rest of the space. The restricted marginal space Π 1 is then extended to Π 1 e = Π 1 × X 1 ⊂ Ω 2. Another stage of learning and testing is performed on Π 1 e obtaining a restricted marginal space Π 2 ⊂ Ω 2 and the procedure is repeated until the full space Ω is reached. At each step, the restricted space Π k is one or two orders of magnitude smaller than Π k−1 × X k . This results in a very efficient algorithm with minimal loss in performance.Figure 2.2 illustrates a simple example for 2D space search. A classifier trained on p(y) can quickly eliminate a large portion of the search space. We can then train a classifier in a much smaller region (region 2 in Fig. 2.2) for the joint distribution p(x, y). Note that MSL is significantly different from a classifier cascade [31]. In a cascade the learning and search are performed in the same space while for MSL the learning and search space is gradually increased.

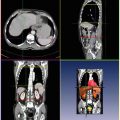
Fig. 2.3
Diagram for 3D object detection using marginal space learning
Let us describe now the general idea of the MSL for 3D object detection. As shown in Fig. 2.3, we split 3D object detection into three steps: position estimation, position-orientation estimation, and position-orientation-scale estimation. The searching order of the subspaces is based on the following considerations. The position of the object in a volume is the most important information, so it should be determined first. The orientation specifies a local object-oriented coordinate system and the scale of the object is defined along the axes of the coordinate system. Since the scale is defined based on a specified orientation, it is estimated after orientation. After each step we keep a limited number of candidates to reduce the search space.
Besides significantly reducing the search space, another advantage of the MSL is that we can use different features or learning methods to estimate the pose parameters in each step. For example, in position estimation, since we treat rotation as an intra-class variation , we can use the efficient 3D Haar wavelet features . In the following steps of position-orientation estimation and position-orientation-scale estimation, we use steerable features , which are efficient to calculate under rotations. Although in our experiments, the same classifier, i.e., the Probabilistic Boosting-Tree (PBT) classifier [28], is used for all estimation steps, it is possible to use different classifiers for different steps.
2.2.3 Training of Position Estimator
To train a classifier, we need to split hypotheses into two groups, positive and negative , based on their distance to the ground truth. The error in object position and scale estimation is not comparable with that of orientation estimation. Therefore, a search-step-normalized distance measure is defined by normalizing the error in each dimension to the corresponding search step size,
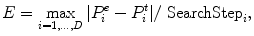
where P i e is the estimated value for parameter i; P i t is the corresponding ground truth; and D is the dimension of the parameter space. For 3D similarity transformation estimation, the pose parameter space is nine dimensional, D = 9. A sample is regarded as a positive one if E ≤ 1. 0 or a negative one if E > 2. 0. The distance from a hypothesis to the ground truth takes a continuous value. It is difficult to draw a clear line to separate positive and negative samples. We intentionally discard samples with a normalized distance between 1.0 and 2.0 to avoid confusing the classifiers.
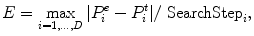
(2.6)
During the position estimation step, learning is constrained in a marginal space with three dimensions. Given a hypothesis (X, Y, Z), the classification problem is formulated as whether there is an object centered at (X, Y, Z). Haar wavelet features are fast to compute and have been shown to be effective for many applications [24, 31]. Therefore, we extended the Haar wavelet features to 3D to be used for learning in this step. Please refer to Sect. 2.3.1 for more information about Haar wavelet features. Note that we tried a position estimator using steerable features and its performance was slightly worse than the Haar wavelet features on some applications, an expected result.
The search step for position estimation is one voxel. According to Eq. (2.6), a positive sample (X, Y, Z) should satisfy
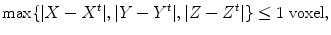
where (X t , Y t , Z t ) is the ground truth of the object center. Normally, there are 23 = 8 position candidates for each training volume satisfying Eq. (2.7) if the position ground truth X t , Y t , and Z t are not on the imaging grid (e.g., X t = 45. 2 voxels). If the ground truth is lying on the imaging grid (e.g., X t = 45 voxels), we may have up to 33 = 27 positive position hypotheses for each training volume.
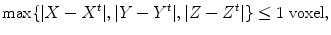
(2.7)
A negative sample is one with
![$$\displaystyle{ \max \{\vert X - {X}^{t}\vert,\vert Y - {Y }^{t}\vert,\vert Z - {Z}^{t}\vert \} > 2\mbox{ voxels}. }$$
” src=”/wp-content/uploads/2016/08/A314110_1_En_2_Chapter_Equ8.gif”></DIV></DIV><br />
<DIV class=EquationNumber>(2.8)</DIV></DIV>Normally, we have far more negative samples than positive ones. The classifier should have the capability to handle such a significantly skewed distribution of positive and negative samples; otherwise, we have to randomly sample roughly the same number of negative samples to match the positive samples .</DIV><br />
<DIV class=Para>The Probabilistic Boosting-Tree (PBT) [<CITE><A href=]() 28] classifier used in most of our experiments has no difficulty to handle uneven distributions of positive and negative samples; therefore, it does not impose constraints on the cardinality of the sample sets.
28] classifier used in most of our experiments has no difficulty to handle uneven distributions of positive and negative samples; therefore, it does not impose constraints on the cardinality of the sample sets.
However, in some applications we still have to subsample the negative samples because of the memory constraints of a desktop computer. On a 32-bit Windows operating system, the maximum amount of memory a program can use is bounded to 2 GB and can be increased to 3 GB with a special setting of Windows, which still limits the number of negative samples that can be loaded into memory. Normally, we train the classifiers on a 64-bit Windows systems with sufficient amount of memory (we tried up to 72 GB of memory). In addition, the memory constraint can be further alleviated by using a computer cluster or a connection to a cloud system.
We often set an upper limit for negative samples (e.g., 10 million) since we need a reasonable speed for the training process. Our training software first gets a rough estimate of the total number of negative samples. If the result is smaller than the upper limit, no sub-sampling is applied; otherwise, we randomly subsample the negative samples to match that limit. We found through experiments that increasing the number of positive samples by adding more training datasets improves substantially the generalization capability of the trained classifiers. Increasing the number of negative samples also helps, however, after a certain level, no further improvement is observed; therefore, random sub-sampling of the negative samples with our current setting (10 million) does not deteriorate the performance of the classifiers.
Given a set of positive and negative training samples, we extract 3D Haar wavelet features and train a classifier (e.g., the PBT). After that, we test each voxel in a volume one by one as a hypothesis of the object position using the trained classifier. As shown in Fig. 2.1a, the classifier assigns each hypothesis a score, and we preserve a small number of candidates (100 in our experiments) with the highest detection score for each volume.
There are various ways to select candidates for the following steps. The first approach is based on the detection score: we keep those candidates with a detection score larger than a threshold. One problem with this approach is that the number of candidates retained varies from volume to volume with a fixed threshold. For a volume with bad image quality, we may find no candidates with a detection score larger than a preset threshold. In many applications, we know there is one and only one target anatomy in a volume. Thus, we select a fixed number of candidates that have the highest detection probability. This approach is more robust and the overall detection speed is consistent from volume to volume.
Sometimes, there may be multiple hypotheses ranking around the cutoff line. For example, if we want to keep 100 hypotheses, we may get five hypotheses with the same score ranking at the 100th. Randomly selecting one from these five hypotheses may introduce randomness in the final detection results, while selecting with a fixed heuristic rule (e.g., selecting the one with the smallest z position) may introduce bias. In our work, we keep all hypotheses ranking around the cutoff line; therefore, the actual number of retained candidates may be slightly larger.
2.2.4 Training of Position-Orientation Estimator
In this step, the task is to jointly estimate the position and orientation. The classification problem is formulated as whether there is an object centered at (X, Y, Z) with orientation (ψ, ϕ, θ). After object position estimation, we preserve the top 100 candidates, (X i , Y i , Z i ), 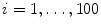 . Since we want to estimate both the position and orientation, we need to augment the dimension of candidates. For each position candidate, we quantize the orientation space uniformly to generate hypotheses. In the experiments on heart chamber detection (see Sect. 2.5), the orientation is represented as three Euler angles in the ZXZ convention, ψ, ϕ, and θ. The distribution range of an Euler angle is estimated from the training data. Each Euler angle is quantized within the range using a step size of 0.2 radians (11 degrees). For each position candidate (X i , Y i , Z i ), we augment it with N (about 1,000) hypotheses of orientation, (X i , Y i , Z i , ψ j , ϕ j , θ j ),
. Since we want to estimate both the position and orientation, we need to augment the dimension of candidates. For each position candidate, we quantize the orientation space uniformly to generate hypotheses. In the experiments on heart chamber detection (see Sect. 2.5), the orientation is represented as three Euler angles in the ZXZ convention, ψ, ϕ, and θ. The distribution range of an Euler angle is estimated from the training data. Each Euler angle is quantized within the range using a step size of 0.2 radians (11 degrees). For each position candidate (X i , Y i , Z i ), we augment it with N (about 1,000) hypotheses of orientation, (X i , Y i , Z i , ψ j , ϕ j , θ j ), 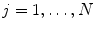 . Some position-orientation hypotheses are close to the ground truth (positive) and others are far away (negative).
. Some position-orientation hypotheses are close to the ground truth (positive) and others are far away (negative).
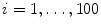 . Since we want to estimate both the position and orientation, we need to augment the dimension of candidates. For each position candidate, we quantize the orientation space uniformly to generate hypotheses. In the experiments on heart chamber detection (see Sect. 2.5), the orientation is represented as three Euler angles in the ZXZ convention, ψ, ϕ, and θ. The distribution range of an Euler angle is estimated from the training data. Each Euler angle is quantized within the range using a step size of 0.2 radians (11 degrees). For each position candidate (X i , Y i , Z i ), we augment it with N (about 1,000) hypotheses of orientation, (X i , Y i , Z i , ψ j , ϕ j , θ j ),
. Since we want to estimate both the position and orientation, we need to augment the dimension of candidates. For each position candidate, we quantize the orientation space uniformly to generate hypotheses. In the experiments on heart chamber detection (see Sect. 2.5), the orientation is represented as three Euler angles in the ZXZ convention, ψ, ϕ, and θ. The distribution range of an Euler angle is estimated from the training data. Each Euler angle is quantized within the range using a step size of 0.2 radians (11 degrees). For each position candidate (X i , Y i , Z i ), we augment it with N (about 1,000) hypotheses of orientation, (X i , Y i , Z i , ψ j , ϕ j , θ j ), 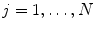 . Some position-orientation hypotheses are close to the ground truth (positive) and others are far away (negative).
. Some position-orientation hypotheses are close to the ground truth (positive) and others are far away (negative).The learning goal is to distinguish the positive and negative samples using a trained classifier. Using the normalized distance measure of Eq. (2.6), a hypothesis (X, Y, Z, ψ, ϕ, θ) is regarded as a positive sample if it satisfies both Eqs. (2.7) and
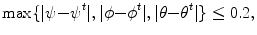
where (ψ t , ϕ t , θ t ) represent the orientation ground truth. A negative sample has either a large position error, satisfying Eq. (2.8), or a large orientation error,
![$$\displaystyle{ \max \{\vert \psi {-\psi }^{t}\vert,\vert \phi {-\phi }^{t}\vert,\vert \theta {-\theta }^{t}\vert \} > 0.4. }$$
” src=”/wp-content/uploads/2016/08/A314110_1_En_2_Chapter_Equ10.gif”></DIV></DIV><br />
<DIV class=EquationNumber>(2.10)</DIV></DIV></DIV><br />
<DIV class=Para>To capture the orientation information, we have to rotate either the volume or feature templates. We use the steerable features (refer to Sect. <SPAN class=InternalRef><A href=]() 2.3.2), which are efficient to extract under rotation. Similarly, the PBT is used for training and the trained classifier is used to prune the hypotheses to preserve only a few candidates (50 in our experiments).
2.3.2), which are efficient to extract under rotation. Similarly, the PBT is used for training and the trained classifier is used to prune the hypotheses to preserve only a few candidates (50 in our experiments).
Get Clinical Tree app for offline access

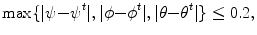
(2.9)
In the above procedure, the positive/negative training samples of the position-orientation classifier are generated from the augmented position candidates. On some datasets, a couple of good position hypotheses that satisfy Eq. (2.7) may be missed after position estimation. We could add them back to generate more position-orientation hypotheses. However, through comparison experiments, we did not find noticeable improvement in the generalization capability of the trained position-orientation estimator. Therefore, the missed good position candidates are not added back during training. Generally, how the classifier is trained should match how the classifier is used. It is preferable to have the same pose hypothesis generation scheme for both the training and testing procedures since during the testing on an unseen volume, we cannot add missed good position candidates back to generate position-orientation hypotheses.
2.2.5 Training of Position-Orientation-Scale Estimator
The training of the position-orientation-scale estimator is analogous to that of the position-orientation estimator except learning is performed in the full nine dimensional similarity transformation space. The dimension of each retained position-orientation candidate is augmented by searching the scale subspace uniformly and exhaustively. The scale search step is set to two voxels. That means a hypothesis (X, Y, Z, ψ, ϕ, θ, S x , S y , S z ) is regarded as a positive sample if, in addition to Eqs. (2.7) and (2.9), it satisfies
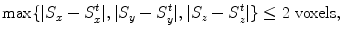
where (S x t , S y t , S z t ) represent the scale ground truth. A negative sample has a large error in position (Eq. (2.8)), orientation (Eq. (2.10)), or scale
![$$\displaystyle{ \max \{\vert S_{x} - S_{x}^{t}\vert,\vert S_{ y} - S_{y}^{t}\vert,\vert S_{ z} - S_{z}^{t}\vert \} > 4\mbox{ voxels}. }$$
” src=”/wp-content/uploads/2016/08/A314110_1_En_2_Chapter_Equ12.gif”></DIV></DIV><br />
<DIV class=EquationNumber>(2.12)</DIV></DIV></DIV></DIV><br />
<DIV id=Sec8 class=]()




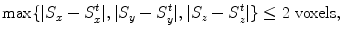
(2.11)
2.2.6 Aggregation of Pose Candidates
The goal of object detection is to obtain a single aggregated estimate of the pose parameters of the object. Multiple detections usually occur around the true object pose since the MSL detectors are insensitive to small changes in the pose parameters. Occasionally, false positives may appear. Some false positives are scattered sparsely, while others may be concentrated around a region that appears similar to the target object.
Intuitively, cluster analysis might help to remove sparsely distributed false positives. However, it is very difficult to perform cluster analysis on a small set of top candidates (e.g., 100) in a nine dimensional pose parameter space. Furthermore, the orientation is represented in a completely different space to the position and scale. To perform clustering we need a distance measurement combining the distances in different marginal spaces. The orientation distance measure needs to be weighted properly to be combined with the position and scale distances. Through experiments, we found that clustering did not improve the accuracy, compared to a simple averaging of the top K (K = 100) candidates.
Since each pose candidate has a classification score given by the PBT classifier , we tried a weighted average scheme by assigning a larger weight to a pose candidate with a higher classification score. However, we did not find significant difference to a simple unweighted average.
The robustness of the aggregation with simple averaging is partially explained by the fact that there are far more good pose hypotheses in 3D than 2D. An exponential increase of pose hypotheses for 3D objection detection also comes with a lot of good hypotheses. For example, there are at least 29 = 512 hypotheses within one search step size from the ground truth. If we include hypotheses within an error of two search step sizes, the total number of good hypotheses increases dramatically to 49 = 262,144. By exploiting the rich image information in a 3D volume and the state-of-the-art learning algorithms, our MSL detectors perform quite well. Most of the preserved top 100 pose candidates are good and the small portion of outliers does not affect too much the detection accuracy after averaging.
Note that the average based aggregation only works if we know a priori that there is only a single instance of the object in the volume. If there might be multiple instances of the same object type (e.g., intervertebral disks of the spine), cluster analysis should be used to select multiple final detection results [19, 20]. To avoid the sparse-sample issue in a high dimensional space, clustering is often performed only for the position component of the pose candidates.
2.2.7 Object Detection in Unseen Volume
This section provides a summary of the testing procedure on an unseen volume. The input volume is first converted to a low isotropic resolution (e.g., 3 mm) matching the volumes in the training set. All voxels are tested using the trained position estimator and the top 100 candidates, (X i , Y i , Z i ), 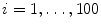 , are kept. Each candidate is augmented with N (about 1,000) hypotheses of orientation, (X i , Y i , Z i , ψ j , ϕ j , θ j ),
, are kept. Each candidate is augmented with N (about 1,000) hypotheses of orientation, (X i , Y i , Z i , ψ j , ϕ j , θ j ), 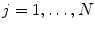 . Next, the trained position-orientation classifier is used to prune these 100 × N hypotheses and the top 50 candidates are retained,
. Next, the trained position-orientation classifier is used to prune these 100 × N hypotheses and the top 50 candidates are retained, 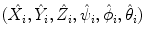 ,
, 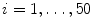 . Similarly, we augment each candidate with M (also about 1,000) hypotheses of scaling and use the trained position-orientation-scale classifier to rank these 50 × M hypotheses. The average of the top K (K = 100) candidates is taken as the final aggregated estimate.
. Similarly, we augment each candidate with M (also about 1,000) hypotheses of scaling and use the trained position-orientation-scale classifier to rank these 50 × M hypotheses. The average of the top K (K = 100) candidates is taken as the final aggregated estimate.
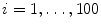 , are kept. Each candidate is augmented with N (about 1,000) hypotheses of orientation, (X i , Y i , Z i , ψ j , ϕ j , θ j ),
, are kept. Each candidate is augmented with N (about 1,000) hypotheses of orientation, (X i , Y i , Z i , ψ j , ϕ j , θ j ), 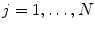 . Next, the trained position-orientation classifier is used to prune these 100 × N hypotheses and the top 50 candidates are retained,
. Next, the trained position-orientation classifier is used to prune these 100 × N hypotheses and the top 50 candidates are retained, 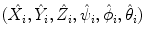 ,
, 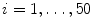 . Similarly, we augment each candidate with M (also about 1,000) hypotheses of scaling and use the trained position-orientation-scale classifier to rank these 50 × M hypotheses. The average of the top K (K = 100) candidates is taken as the final aggregated estimate.
. Similarly, we augment each candidate with M (also about 1,000) hypotheses of scaling and use the trained position-orientation-scale classifier to rank these 50 × M hypotheses. The average of the top K (K = 100) candidates is taken as the final aggregated estimate.In the following, we analyze the computational complexity of heart chamber detection from a cardiac CT volume [34]. For position estimation, all voxels (about 260,000 voxels for a small volume with 64 × 64 × 64 voxels at the 3 mm resolution) are tested for possible object position. There are about 1,000 hypotheses for orientation and scale each. If the parameter space is searched uniformly and exhaustively, there are about 2. 6 × 1011 hypotheses to be tested! However, using MSL, we only test about 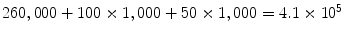 hypotheses and reduce the testing by almost six orders of magnitude.
hypotheses and reduce the testing by almost six orders of magnitude.
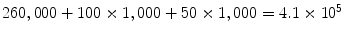 hypotheses and reduce the testing by almost six orders of magnitude.
hypotheses and reduce the testing by almost six orders of magnitude.In practice, an irrelevant volume might be fed into the automatic detection and segmentation system due to mis-labeling. For example, the input data to a heart chamber segmentation system may be an abdominal scan without the heart in the volume at all. There are different strategies to handle such situation.
One is the “garbage-in garbage-out” principle, in which the algorithm just tries its best to produce the best segmentation it can achieve. All segmentation results will eventually be double checked by a physician and a non-meaningful segmentation result on a wrong input data can be easily identified and discarded. In the second strategy, the automatic segmentation algorithm is expected to intelligently tell if a target anatomy is present in the data or not. Depending on the presence or absence of the target anatomy, different processing workflows may be invoked later on. In such scenario, a threshold can be set to reject a wrong input. For example, we check the maximum detection score of the preserved position candidates. If it is less than a pre-set threshold, the data is rejected. Normally, we set the threshold very low to avoid rejecting a good input data. Wrong results can later be rejected in the subsequent detection pipelines, e.g., position-orientation estimation and position-orientation-scale estimation.
2.3 3D Image Features
The MSL is an open and flexible object detection framework. Any image features can be integrated into the framework as long as they can provide some information to discriminate between positive and negative hypotheses. In this section, we present two kinds of 3D image features used in a specific implementation of MSL for heart chamber detection in cardiac CT volumes (as presented in Sect. 2.5). The Haar wavelet features are used for object position estimation and the steerable features, capable of encoding the orientation hypothesis, are used for position-orientation estimation and position-orientation-scale estimation. In fact, these two kinds of features work well on multiple object detection problems in major imaging modalities, including ultrasound data.
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree