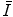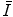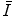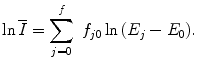(1)
Amersham, Buckinghamshire, UK
Abstract
The mean excitation energy, 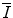 , appears in the logarithmic term of the soft collision stopping power. In practice, it is determined through extraction from measurements of the energy loss of a charged particle traversing a medium. However, there remains significant interest in understanding the theoretical aspects of the parameter, including deriving it ab initio and discovering that quite simplistic models can recreate the fundamental physical properties of
, appears in the logarithmic term of the soft collision stopping power. In practice, it is determined through extraction from measurements of the energy loss of a charged particle traversing a medium. However, there remains significant interest in understanding the theoretical aspects of the parameter, including deriving it ab initio and discovering that quite simplistic models can recreate the fundamental physical properties of 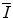 . In this chapter, theoretical models of increasing complexity are considered in the calculation of the mean excitation energy. The chapter is concluded with a review of the mechanisms of experimental determination of
. In this chapter, theoretical models of increasing complexity are considered in the calculation of the mean excitation energy. The chapter is concluded with a review of the mechanisms of experimental determination of 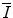 and parameterisations of the quantity. Although the latter are of limited practical use since tabulated values of
and parameterisations of the quantity. Although the latter are of limited practical use since tabulated values of 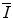 exist, it is of historical interest to consider them.
exist, it is of historical interest to consider them.
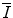 , appears in the logarithmic term of the soft collision stopping power. In practice, it is determined through extraction from measurements of the energy loss of a charged particle traversing a medium. However, there remains significant interest in understanding the theoretical aspects of the parameter, including deriving it ab initio and discovering that quite simplistic models can recreate the fundamental physical properties of
, appears in the logarithmic term of the soft collision stopping power. In practice, it is determined through extraction from measurements of the energy loss of a charged particle traversing a medium. However, there remains significant interest in understanding the theoretical aspects of the parameter, including deriving it ab initio and discovering that quite simplistic models can recreate the fundamental physical properties of 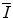 . In this chapter, theoretical models of increasing complexity are considered in the calculation of the mean excitation energy. The chapter is concluded with a review of the mechanisms of experimental determination of
. In this chapter, theoretical models of increasing complexity are considered in the calculation of the mean excitation energy. The chapter is concluded with a review of the mechanisms of experimental determination of 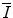 and parameterisations of the quantity. Although the latter are of limited practical use since tabulated values of
and parameterisations of the quantity. Although the latter are of limited practical use since tabulated values of 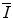 exist, it is of historical interest to consider them.
exist, it is of historical interest to consider them.11.1 Introductory Comments
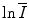 is a property of the medium alone and is independent of the nature of the charged projectile. Further, as
is a property of the medium alone and is independent of the nature of the charged projectile. Further, as 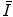 resides within the argument of a logarithm, changes and uncertainties in its value can have limited effects upon the value of the collision stopping power.
resides within the argument of a logarithm, changes and uncertainties in its value can have limited effects upon the value of the collision stopping power.Values of 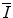 can be determined through both theoretical or experimental means. Because of the complexities inherent to the calculation and the need of knowledge of the atomic wavefunction, ab initio calculations of
can be determined through both theoretical or experimental means. Because of the complexities inherent to the calculation and the need of knowledge of the atomic wavefunction, ab initio calculations of 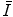 have tended to be limited to monatomic gases of low atomic number. As such, the number of elements for which
have tended to be limited to monatomic gases of low atomic number. As such, the number of elements for which 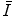 has been calculated is small with the result that
has been calculated is small with the result that 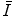 is obtained largely through measurement. Both theoretical and experimental methods of evaluating
is obtained largely through measurement. Both theoretical and experimental methods of evaluating 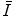 are investigated in this chapter.
are investigated in this chapter.
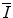 can be determined through both theoretical or experimental means. Because of the complexities inherent to the calculation and the need of knowledge of the atomic wavefunction, ab initio calculations of
can be determined through both theoretical or experimental means. Because of the complexities inherent to the calculation and the need of knowledge of the atomic wavefunction, ab initio calculations of 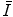 have tended to be limited to monatomic gases of low atomic number. As such, the number of elements for which
have tended to be limited to monatomic gases of low atomic number. As such, the number of elements for which 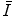 has been calculated is small with the result that
has been calculated is small with the result that 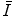 is obtained largely through measurement. Both theoretical and experimental methods of evaluating
is obtained largely through measurement. Both theoretical and experimental methods of evaluating 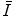 are investigated in this chapter.
are investigated in this chapter.We begin our discussion of the mean excitation energy with the theoretical means of determining the quantity. This is done, at first, by a very simple (and crude) estimate based upon the ratio of the Bohr velocity and atomic radius. Despite its crudeness, the estimate yields a surprisingly reasonable result. Then, following the work of Bloch (1933), we derive a more elegant means of calculating 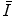 using the Thomas–Fermi model of the atom that we derived in Chap. 5. We also examine the optical dipole oscillator strength and the local plasma approximation as approaches to calculating
using the Thomas–Fermi model of the atom that we derived in Chap. 5. We also examine the optical dipole oscillator strength and the local plasma approximation as approaches to calculating 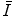 .
.
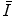 using the Thomas–Fermi model of the atom that we derived in Chap. 5. We also examine the optical dipole oscillator strength and the local plasma approximation as approaches to calculating
using the Thomas–Fermi model of the atom that we derived in Chap. 5. We also examine the optical dipole oscillator strength and the local plasma approximation as approaches to calculating 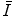 .
.Following this, we look at the considerations that must be accounted for in the experimental determination of 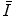 and the means of how it is measured. We then consider parameterisations of
and the means of how it is measured. We then consider parameterisations of 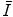 as a function of Z which can be useful in practical medical radiation physics calculations instead of using tabular data.
as a function of Z which can be useful in practical medical radiation physics calculations instead of using tabular data.
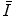 and the means of how it is measured. We then consider parameterisations of
and the means of how it is measured. We then consider parameterisations of 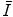 as a function of Z which can be useful in practical medical radiation physics calculations instead of using tabular data.
as a function of Z which can be useful in practical medical radiation physics calculations instead of using tabular data.Additional discussions of the mean excitation energy can be found in those reviews by Uehling (1954) and Fano (1964) and in ICRU Reports 37 (1984) and 49 (1993).
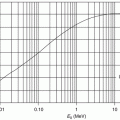
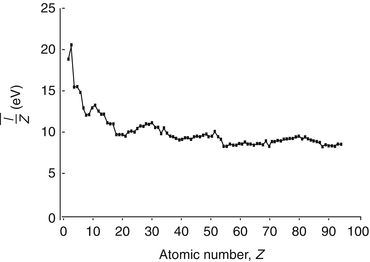
The general characteristics of 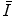 can be seen in Fig. 11.1 in which the mean excitation energy normalised to the atomic number for elements is shown as a function of atomic number. These data are from ICRU Report 37 and are largely based upon the
can be seen in Fig. 11.1 in which the mean excitation energy normalised to the atomic number for elements is shown as a function of atomic number. These data are from ICRU Report 37 and are largely based upon the 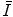 values obtained from energy loss transmission measurements of high-energy protons, as described in Sect. 11.3. It can be seen that this ratio decreases rapidly to a constant value of about 10 eV for Z greater than about 15. However, it is also seen that superimposed upon this general trend are discontinuities which can be attributed to the effects of atomic shell structure.
values obtained from energy loss transmission measurements of high-energy protons, as described in Sect. 11.3. It can be seen that this ratio decreases rapidly to a constant value of about 10 eV for Z greater than about 15. However, it is also seen that superimposed upon this general trend are discontinuities which can be attributed to the effects of atomic shell structure.
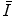 can be seen in Fig. 11.1 in which the mean excitation energy normalised to the atomic number for elements is shown as a function of atomic number. These data are from ICRU Report 37 and are largely based upon the
can be seen in Fig. 11.1 in which the mean excitation energy normalised to the atomic number for elements is shown as a function of atomic number. These data are from ICRU Report 37 and are largely based upon the 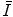 values obtained from energy loss transmission measurements of high-energy protons, as described in Sect. 11.3. It can be seen that this ratio decreases rapidly to a constant value of about 10 eV for Z greater than about 15. However, it is also seen that superimposed upon this general trend are discontinuities which can be attributed to the effects of atomic shell structure.
values obtained from energy loss transmission measurements of high-energy protons, as described in Sect. 11.3. It can be seen that this ratio decreases rapidly to a constant value of about 10 eV for Z greater than about 15. However, it is also seen that superimposed upon this general trend are discontinuities which can be attributed to the effects of atomic shell structure.
Fig. 11.1
Mean excitation energy normalised to the atomic number for elements as a function of atomic number (Data are from ICRU Report 37 (1984))
11.2 Theoretical Evaluations of 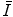
11.2.1 Introductory Comments
A theoretical evaluation of 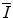 will likely have limited application to medical radiation physics calculations. The desired accuracy in the numerical value of the quantity will be best provided by experiment, as discussed in Sect. 11.3. Even so, a theoretical understanding of
will likely have limited application to medical radiation physics calculations. The desired accuracy in the numerical value of the quantity will be best provided by experiment, as discussed in Sect. 11.3. Even so, a theoretical understanding of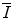 can be revelatory by showing facets of the underlying physics that plays a role in the features of the mean excitation energy. In this section, we review a number of theoretical means of calculating
can be revelatory by showing facets of the underlying physics that plays a role in the features of the mean excitation energy. In this section, we review a number of theoretical means of calculating 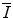 ab initio.
ab initio.
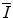 will likely have limited application to medical radiation physics calculations. The desired accuracy in the numerical value of the quantity will be best provided by experiment, as discussed in Sect. 11.3. Even so, a theoretical understanding of
will likely have limited application to medical radiation physics calculations. The desired accuracy in the numerical value of the quantity will be best provided by experiment, as discussed in Sect. 11.3. Even so, a theoretical understanding of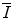 can be revelatory by showing facets of the underlying physics that plays a role in the features of the mean excitation energy. In this section, we review a number of theoretical means of calculating
can be revelatory by showing facets of the underlying physics that plays a role in the features of the mean excitation energy. In this section, we review a number of theoretical means of calculating 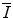 ab initio.
ab initio.11.2.2 Ratio of Bohr Velocity to Bohr Radius
We can estimate crudely the dependence of the excitation energy upon the atomic number of the atom by treating the atomic electrons as oscillators and by approximating the atomic electron orbital frequency with the ratio of the Bohr velocity to the Bohr radius:
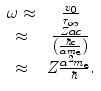
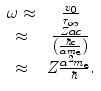
(11.2)
Then, the mean excitation energy is
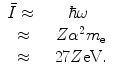
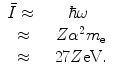
(11.3)
There should be no doubt that this is a crude model. However, the result suggests that the ratio of the mean excitation energy of a monatomic medium to its atomic number, 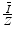 , is a constant, which was shown to be reasonably true for
, is a constant, which was shown to be reasonably true for ![$$ Z>15 $$” src=”/wp-content/uploads/2016/04/A306762_1_En_11_Chapter_IEq001123.gif”></SPAN> in Fig. <SPAN class=InternalRef><A href=]() 11.1. The constant of proportionality in (11.3) is to be expected to be an overestimate as we have used the Bohr velocity for the ground state,
11.1. The constant of proportionality in (11.3) is to be expected to be an overestimate as we have used the Bohr velocity for the ground state, 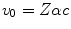 , which is the fastest of the atomic electrons. If we were to instead use the arithmetic mean and approximate a mean Bohr velocity,
, which is the fastest of the atomic electrons. If we were to instead use the arithmetic mean and approximate a mean Bohr velocity, 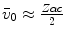 , we obtain
, we obtain
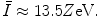
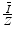 , is a constant, which was shown to be reasonably true for
, is a constant, which was shown to be reasonably true for 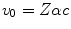 , which is the fastest of the atomic electrons. If we were to instead use the arithmetic mean and approximate a mean Bohr velocity,
, which is the fastest of the atomic electrons. If we were to instead use the arithmetic mean and approximate a mean Bohr velocity, 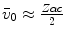 , we obtain
, we obtain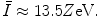
(11.4)
Quantitatively, this new result is closer to the results obtained from experiment as shown in Fig. 11.1.
11.2.3 Thomas–Fermi Model
Another means of estimating 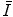 is through the statistical model of Thomas and Fermi in describing the atom. This model was derived in Sect. 5.3.5 in the context of describing the atomic electron screening of the nuclear Coulomb potential. Recall that the radius of the Thomas–Fermi atom is defined as
is through the statistical model of Thomas and Fermi in describing the atom. This model was derived in Sect. 5.3.5 in the context of describing the atomic electron screening of the nuclear Coulomb potential. Recall that the radius of the Thomas–Fermi atom is defined as
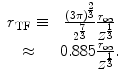
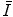 is through the statistical model of Thomas and Fermi in describing the atom. This model was derived in Sect. 5.3.5 in the context of describing the atomic electron screening of the nuclear Coulomb potential. Recall that the radius of the Thomas–Fermi atom is defined as
is through the statistical model of Thomas and Fermi in describing the atom. This model was derived in Sect. 5.3.5 in the context of describing the atomic electron screening of the nuclear Coulomb potential. Recall that the radius of the Thomas–Fermi atom is defined as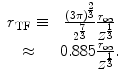
We will crudely model the atom as being a homogeneous sphere of negative charge –Ze surrounding a point charge +Ze. The sphere, or electron ‘cloud’, will be subject to two sources of potential energy, one due to the self-energy of the electrons, which we refer to as U e, and the other due to that of the Coulomb interaction with the nucleus, which is referred to as U n. In addition, there will be a kinetic energy contribution. Let us now evaluate these three sources.
First, we evaluate the self-energy, U e . Consider the electron sphere to have a radius r TF for a net charge of –Ze. Because of the assumption of the negative charge homogeneity, the negative charge density within the sphere is
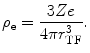
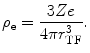
(11.5)
Then, the self-energy term is
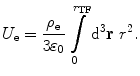
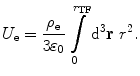
(11.6)
The integration of (11.6) results in
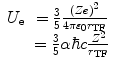
where the definition of the fine-structure constant has been introduced in order to simplify the form of the expression.
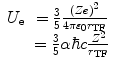
(11.7)
The second term consists of the energy that is required to bring the nucleus from infinity to the edge of the electron cloud and then to the centre. We label these two individual terms as U n1 and U n2, respectively. The first is simply
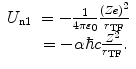
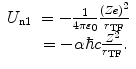
(11.8)
To calculate 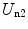 , we note that the electric field within the sphere is
, we note that the electric field within the sphere is
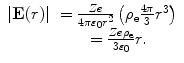
 , we note that the electric field within the sphere is
, we note that the electric field within the sphere is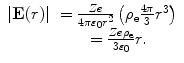
(11.9)
Then, the energy required to bring the nucleus to the centre of the electron cloud is
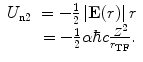
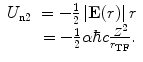
(11.10)
Thus, the potential energy of the electron cloud containing the nucleus is the sum of 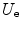 ,
, 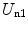 and
and 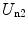 , or
, or
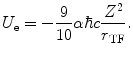
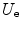 ,
, 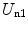 and
and 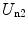 , or
, or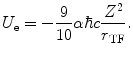
(11.11)
We now calculate the kinetic energy using the Fermi gas model (see Section 3.3 of McParland (2010) for a derivation of that model). The mean energy of the electron states is given by
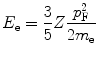
where 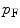




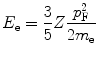
(11.12)
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree