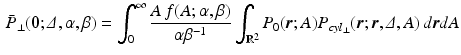in human subjects, enabling the measurement of the ensemble average propagator (EAP) at distances as short as 10  . Coupled with continuous models of the full 3D DWI signal and the EAP such as Mean Apparent Propagator (MAP) MRI, these acquisition schemes provide unparalleled means to probe the WM tissue in vivo. Presently, there are two complementary limitations in tractography and microstructure measurement techniques. Tractography techniques are based on models of the DWI signal geometry without taking specific hypotheses of the WM structure. This hinders the tracing of fascicles through certain WM areas with complex organization such as branching, crossing, merging, and bottlenecks that are indistinguishable using the orientation-only part of the DWI signal. Microstructure measuring techniques, such as AxCaliber, require the direction of the axons within the probed tissue before the acquisition as well as the tissue to be highly organized. Our contributions are twofold. First, we extend the theoretical DWI models proposed by Callaghan et al. to characterize the distribution of axonal calibers within the probed tissue taking advantage of the MAP-MRI model. Second, we develop a simultaneous tractography and axonal caliber distribution algorithm based on the hypothesis that axonal caliber distribution varies smoothly along a WM fascicle. To validate our model we test it on in-silico phantoms and on the HCP dataset.
. Coupled with continuous models of the full 3D DWI signal and the EAP such as Mean Apparent Propagator (MAP) MRI, these acquisition schemes provide unparalleled means to probe the WM tissue in vivo. Presently, there are two complementary limitations in tractography and microstructure measurement techniques. Tractography techniques are based on models of the DWI signal geometry without taking specific hypotheses of the WM structure. This hinders the tracing of fascicles through certain WM areas with complex organization such as branching, crossing, merging, and bottlenecks that are indistinguishable using the orientation-only part of the DWI signal. Microstructure measuring techniques, such as AxCaliber, require the direction of the axons within the probed tissue before the acquisition as well as the tissue to be highly organized. Our contributions are twofold. First, we extend the theoretical DWI models proposed by Callaghan et al. to characterize the distribution of axonal calibers within the probed tissue taking advantage of the MAP-MRI model. Second, we develop a simultaneous tractography and axonal caliber distribution algorithm based on the hypothesis that axonal caliber distribution varies smoothly along a WM fascicle. To validate our model we test it on in-silico phantoms and on the HCP dataset.
1 Introduction
2 Theory
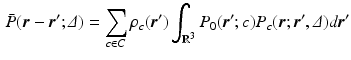
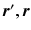 are the particle’s start and end positions;
are the particle’s start and end positions; 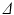 the diffusion time; C is the set of compartments;
the diffusion time; C is the set of compartments; 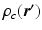 is the probability of
is the probability of 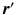 being inside compartment c;
being inside compartment c; 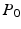 the probability of the initial position in c; and
the probability of the initial position in c; and 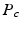 the compartment-specific propagator. The EAP is related to the attenuation of the DWI signal by the Fourier transform:
the compartment-specific propagator. The EAP is related to the attenuation of the DWI signal by the Fourier transform: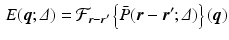
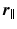 with negligible tortuosity and permeability, the displacement
with negligible tortuosity and permeability, the displacement 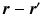 is decomposable in the parallel and perpendicular directions to the cylinder [4]. We write this as
is decomposable in the parallel and perpendicular directions to the cylinder [4]. We write this as 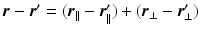 leading to separable formulations of P and E [4]:
leading to separable formulations of P and E [4]: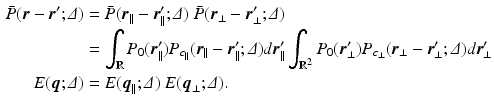
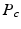 [6]. If the propagator
[6]. If the propagator 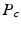 is measured at a cylinder of cross-sectional area A and it’s filled with water with diffusion coefficient D, we derive the following expressions [6]:
is measured at a cylinder of cross-sectional area A and it’s filled with water with diffusion coefficient D, we derive the following expressions [6]: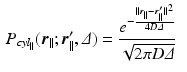
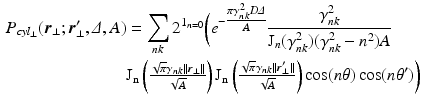
 is the indicator function for
is the indicator function for 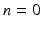 ,
, 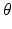 and
and 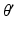 are the respective angles of
are the respective angles of 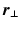 and
and 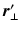 when expressed in polar coordinates,
when expressed in polar coordinates, 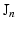 is the n-th cylindrical Bessel function and
is the n-th cylindrical Bessel function and 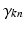 the k-th the root of its derivative:
the k-th the root of its derivative: 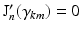 .
.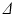 dimensions; ActiveAx estimates a single-parameter which experimentally correlates with the mean caliber without an explicit formal relationship to it; and RTAP which needs very large diffusion times (
dimensions; ActiveAx estimates a single-parameter which experimentally correlates with the mean caliber without an explicit formal relationship to it; and RTAP which needs very large diffusion times (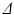 ) for the perpendicular EAP to become [11]
) for the perpendicular EAP to become [11]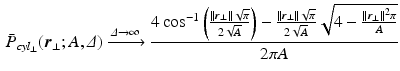
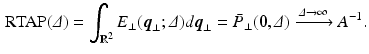
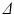 values, the propagator along the cylinder has a specific relationship with the distribution of cross-sectional areas in a cylinder population. We base our model on the EAP as opposed to the AxCaliber and RTAP approaches which focus on the signal attenuation. This has the main advantage of simultaneously modelling, through the Fourier slice theorem, all measurements on the perpendicular plane to the cylinder population. We start our model in the style of AxCaliber and “infinite
values, the propagator along the cylinder has a specific relationship with the distribution of cross-sectional areas in a cylinder population. We base our model on the EAP as opposed to the AxCaliber and RTAP approaches which focus on the signal attenuation. This has the main advantage of simultaneously modelling, through the Fourier slice theorem, all measurements on the perpendicular plane to the cylinder population. We start our model in the style of AxCaliber and “infinite 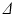 ” RTAP, we attach a density to the cross-sectional area of a cylinder population. Our density is based on three hypotheses given by Özarslan et al. [11]. First, each particular cylinder’s contribution to the overall signal is proportional to the ratio of water particles in it, which is in direct relationship with the cylinder’s cross-sectional area. Second, the cylinder population is Gamma-distributed [3]. This leads to specific EAP formulation, Eq. (1), for N cylinders:
” RTAP, we attach a density to the cross-sectional area of a cylinder population. Our density is based on three hypotheses given by Özarslan et al. [11]. First, each particular cylinder’s contribution to the overall signal is proportional to the ratio of water particles in it, which is in direct relationship with the cylinder’s cross-sectional area. Second, the cylinder population is Gamma-distributed [3]. This leads to specific EAP formulation, Eq. (1), for N cylinders: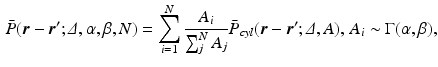
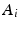 is an independent and identically distributed random variable with Gamma distribution, of shape
is an independent and identically distributed random variable with Gamma distribution, of shape 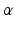 and rate
and rate 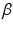 , of the cross-sectional area. Finally, our third hypothesis assumes that the population is large enough to be approximated by an infinite number of cylinders. Combining Equations 1 and 5
, of the cross-sectional area. Finally, our third hypothesis assumes that the population is large enough to be approximated by an infinite number of cylinders. Combining Equations 1 and 5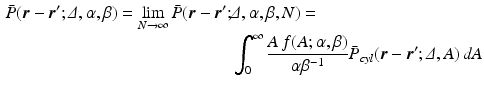
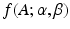 is the probability density function of a Gamma distribution with shape
is the probability density function of a Gamma distribution with shape 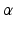 and rate
and rate 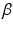 ; and
; and 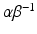 is the average cross-sectional area under the distribution
is the average cross-sectional area under the distribution 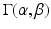 . By using the separability of the EAP (see Eq. 3) and assuming a uniform probability of finding a water particle within the cylinder population, we marginalize Eq. 6 for the return-to-axis probability, i.e.
. By using the separability of the EAP (see Eq. 3) and assuming a uniform probability of finding a water particle within the cylinder population, we marginalize Eq. 6 for the return-to-axis probability, i.e. 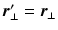 ,
,