(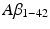 ) peptide, increasing CSF tau protein and neurodegeneration, characterized by cerebral atrophy and neuron loss. In order to increase the chances of success of a given treatment, the need for an early diagnosis and the need to understand the progression of the disease are crucial.
) peptide, increasing CSF tau protein and neurodegeneration, characterized by cerebral atrophy and neuron loss. In order to increase the chances of success of a given treatment, the need for an early diagnosis and the need to understand the progression of the disease are crucial.
Longitudinal data, which consists in repeated observations of a given individual or group of individuals over time, allows to study the progression of a disease and the statistical analysis of longitudinal data may provide useful informations to help diagnose AD in its early phase. Mixed effects models provide a rich framework to analyze longitudinal measurements. The fixed (and respectively random) effects allow to describe the model at the group (respectively subject) level and the distribution of the random effects accounts for inter-subject variability. A particular case of the linear mixed-effects models introduced by Laird and Ware in [5] can be used to model a linear relationship between univariate longitudinal measurement and the times of observation : the random slope and intercept model. If 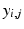 denotes the j-th observation of the i-th subject associated to time
denotes the j-th observation of the i-th subject associated to time 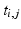 , the random slope and intercept model would write :
, the random slope and intercept model would write : 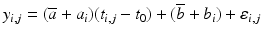 , where
, where 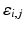 denotes a Gaussian noise with zero mean. The fixed effects
denotes a Gaussian noise with zero mean. The fixed effects 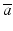 and
and 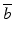 respectively correspond to the slope and intercept of an average trajectory
respectively correspond to the slope and intercept of an average trajectory 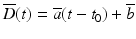 whereas
whereas 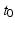 plays the role of a reference time. The subject-specific slope
plays the role of a reference time. The subject-specific slope 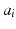 and
and 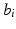 correspond to the slope and intercept of the trajectory of the i-th individual.
correspond to the slope and intercept of the trajectory of the i-th individual.
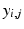 denotes the j-th observation of the i-th subject associated to time
denotes the j-th observation of the i-th subject associated to time 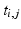 , the random slope and intercept model would write :
, the random slope and intercept model would write : 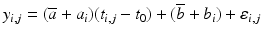 , where
, where 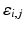 denotes a Gaussian noise with zero mean. The fixed effects
denotes a Gaussian noise with zero mean. The fixed effects 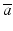 and
and 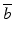 respectively correspond to the slope and intercept of an average trajectory
respectively correspond to the slope and intercept of an average trajectory 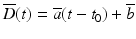 whereas
whereas 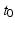 plays the role of a reference time. The subject-specific slope
plays the role of a reference time. The subject-specific slope 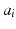 and
and 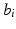 correspond to the slope and intercept of the trajectory of the i-th individual.
correspond to the slope and intercept of the trajectory of the i-th individual.If the longitudinal observations arise, for example, from developmental studies, breeding studies or pharmacological studies, there is a natural choice for the baseline time 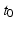 , which may represent the time of birth, beginning of the study or time at which a certain drug has been administered. In those situations, the baseline time is known and is therefore not estimated along with the parameters of the model. However, in studies on neurodegenerative diseases, such as Alzheimer’s disease, there may be no natural choice for the reference time. As pointed out by Yang et al. in [4] and Delor et al. in [3], the disease-onset time is probably different for every individual and, at a given age, two individuals may be at very different stages of disease progression. When the baseline (or disease-onset) time is unknown, one may consider it as a fixed effect of the given model. In [2], the authors proposed an interesting mixed-effect model for scalar measurements but the model did not account for the difference in stages progression among individuals. Yang et al. [4] and Delor et al. [3] addressed this issue by including time shifts in their models but Yang et al. did not estimate the time shifts in a statistical framework. In Delor et al., the observations of a given individual were shifted in time before the estimation of a disease-onset time. In both situations, the reference time was not estimated. In [8], Singh et al. proposed an interesting model for longitudinal manifold-valued observations using parallel transport. However, if the model is written for univariate longitudinal data, the model does include a random effect to account for the variability in speed of disease progression.
, which may represent the time of birth, beginning of the study or time at which a certain drug has been administered. In those situations, the baseline time is known and is therefore not estimated along with the parameters of the model. However, in studies on neurodegenerative diseases, such as Alzheimer’s disease, there may be no natural choice for the reference time. As pointed out by Yang et al. in [4] and Delor et al. in [3], the disease-onset time is probably different for every individual and, at a given age, two individuals may be at very different stages of disease progression. When the baseline (or disease-onset) time is unknown, one may consider it as a fixed effect of the given model. In [2], the authors proposed an interesting mixed-effect model for scalar measurements but the model did not account for the difference in stages progression among individuals. Yang et al. [4] and Delor et al. [3] addressed this issue by including time shifts in their models but Yang et al. did not estimate the time shifts in a statistical framework. In Delor et al., the observations of a given individual were shifted in time before the estimation of a disease-onset time. In both situations, the reference time was not estimated. In [8], Singh et al. proposed an interesting model for longitudinal manifold-valued observations using parallel transport. However, if the model is written for univariate longitudinal data, the model does include a random effect to account for the variability in speed of disease progression.
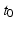 , which may represent the time of birth, beginning of the study or time at which a certain drug has been administered. In those situations, the baseline time is known and is therefore not estimated along with the parameters of the model. However, in studies on neurodegenerative diseases, such as Alzheimer’s disease, there may be no natural choice for the reference time. As pointed out by Yang et al. in [4] and Delor et al. in [3], the disease-onset time is probably different for every individual and, at a given age, two individuals may be at very different stages of disease progression. When the baseline (or disease-onset) time is unknown, one may consider it as a fixed effect of the given model. In [2], the authors proposed an interesting mixed-effect model for scalar measurements but the model did not account for the difference in stages progression among individuals. Yang et al. [4] and Delor et al. [3] addressed this issue by including time shifts in their models but Yang et al. did not estimate the time shifts in a statistical framework. In Delor et al., the observations of a given individual were shifted in time before the estimation of a disease-onset time. In both situations, the reference time was not estimated. In [8], Singh et al. proposed an interesting model for longitudinal manifold-valued observations using parallel transport. However, if the model is written for univariate longitudinal data, the model does include a random effect to account for the variability in speed of disease progression.
, which may represent the time of birth, beginning of the study or time at which a certain drug has been administered. In those situations, the baseline time is known and is therefore not estimated along with the parameters of the model. However, in studies on neurodegenerative diseases, such as Alzheimer’s disease, there may be no natural choice for the reference time. As pointed out by Yang et al. in [4] and Delor et al. in [3], the disease-onset time is probably different for every individual and, at a given age, two individuals may be at very different stages of disease progression. When the baseline (or disease-onset) time is unknown, one may consider it as a fixed effect of the given model. In [2], the authors proposed an interesting mixed-effect model for scalar measurements but the model did not account for the difference in stages progression among individuals. Yang et al. [4] and Delor et al. [3] addressed this issue by including time shifts in their models but Yang et al. did not estimate the time shifts in a statistical framework. In Delor et al., the observations of a given individual were shifted in time before the estimation of a disease-onset time. In both situations, the reference time was not estimated. In [8], Singh et al. proposed an interesting model for longitudinal manifold-valued observations using parallel transport. However, if the model is written for univariate longitudinal data, the model does include a random effect to account for the variability in speed of disease progression.When the time reference time 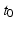 is considered unknown, the linear model given above is not identifiable and there is a relation between the distribution of the intercept random effect
is considered unknown, the linear model given above is not identifiable and there is a relation between the distribution of the intercept random effect 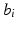 and the fixed effect
and the fixed effect 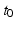 , which makes the interpretation of the distribution of the intercept random effect
, which makes the interpretation of the distribution of the intercept random effect 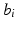 difficult.
difficult.
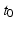 is considered unknown, the linear model given above is not identifiable and there is a relation between the distribution of the intercept random effect
is considered unknown, the linear model given above is not identifiable and there is a relation between the distribution of the intercept random effect 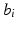 and the fixed effect
and the fixed effect 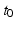 , which makes the interpretation of the distribution of the intercept random effect
, which makes the interpretation of the distribution of the intercept random effect 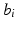 difficult.
difficult.To address the issues we pointed out, we propose to replace the intercept random effect 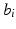 , which characterizes the distribution of the measurement values at time
, which characterizes the distribution of the measurement values at time 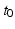 , by a time shift
, by a time shift 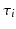 which measures the delay (or advance) in disease progression. We therefore consider the model :
which measures the delay (or advance) in disease progression. We therefore consider the model : 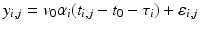 where
where 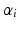 is a random effect log-normally distributed with mean equal to 1 and
is a random effect log-normally distributed with mean equal to 1 and 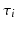 is the time shift random effect normally distributed with mean 0. The fixed effect
is the time shift random effect normally distributed with mean 0. The fixed effect 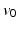 correspond to the slope of the mean trajectory and is the fixed effect associated to
correspond to the slope of the mean trajectory and is the fixed effect associated to 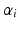 whereas
whereas 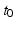 is now the fixed effect associated to the random effect
is now the fixed effect associated to the random effect 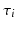 . If D denotes the straight line
. If D denotes the straight line 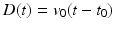 , the model writes :
, the model writes : 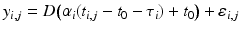 . As a consequence, the random effects
. As a consequence, the random effects 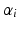 and
and 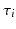 allow to define a subject-specific affine reparametrization of the straight line D, which can be thought of as an average trajectory. The acceleration factor
allow to define a subject-specific affine reparametrization of the straight line D, which can be thought of as an average trajectory. The acceleration factor 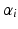 and the time shift
and the time shift 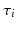 of the affine subject-specific reparametrization provide informations on the dynamical evolution of a given subject with respect to the average model: the acceleration factor will determine whether an individual is progressing faster than the individual trajectory. The time shift determines whether the individual is lagging behind or ahead of the average model. Therefore, the random effects of the model will allow to determine, among a group of individuals, who are fast or slow progressing individuals and whether a given individual might develop the disease earlier (early-onset) or later (late-onset) than the estimated reference time
of the affine subject-specific reparametrization provide informations on the dynamical evolution of a given subject with respect to the average model: the acceleration factor will determine whether an individual is progressing faster than the individual trajectory. The time shift determines whether the individual is lagging behind or ahead of the average model. Therefore, the random effects of the model will allow to determine, among a group of individuals, who are fast or slow progressing individuals and whether a given individual might develop the disease earlier (early-onset) or later (late-onset) than the estimated reference time 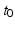 .
.
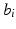 , which characterizes the distribution of the measurement values at time
, which characterizes the distribution of the measurement values at time 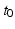 , by a time shift
, by a time shift 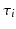 which measures the delay (or advance) in disease progression. We therefore consider the model :
which measures the delay (or advance) in disease progression. We therefore consider the model : 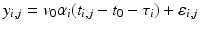 where
where 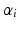 is a random effect log-normally distributed with mean equal to 1 and
is a random effect log-normally distributed with mean equal to 1 and 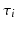 is the time shift random effect normally distributed with mean 0. The fixed effect
is the time shift random effect normally distributed with mean 0. The fixed effect 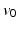 correspond to the slope of the mean trajectory and is the fixed effect associated to
correspond to the slope of the mean trajectory and is the fixed effect associated to 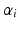 whereas
whereas 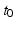 is now the fixed effect associated to the random effect
is now the fixed effect associated to the random effect 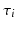 . If D denotes the straight line
. If D denotes the straight line 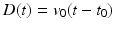 , the model writes :
, the model writes : 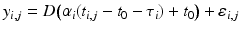 . As a consequence, the random effects
. As a consequence, the random effects 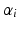 and
and 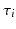 allow to define a subject-specific affine reparametrization of the straight line D, which can be thought of as an average trajectory. The acceleration factor
allow to define a subject-specific affine reparametrization of the straight line D, which can be thought of as an average trajectory. The acceleration factor 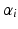 and the time shift
and the time shift 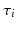 of the affine subject-specific reparametrization provide informations on the dynamical evolution of a given subject with respect to the average model: the acceleration factor will determine whether an individual is progressing faster than the individual trajectory. The time shift determines whether the individual is lagging behind or ahead of the average model. Therefore, the random effects of the model will allow to determine, among a group of individuals, who are fast or slow progressing individuals and whether a given individual might develop the disease earlier (early-onset) or later (late-onset) than the estimated reference time
of the affine subject-specific reparametrization provide informations on the dynamical evolution of a given subject with respect to the average model: the acceleration factor will determine whether an individual is progressing faster than the individual trajectory. The time shift determines whether the individual is lagging behind or ahead of the average model. Therefore, the random effects of the model will allow to determine, among a group of individuals, who are fast or slow progressing individuals and whether a given individual might develop the disease earlier (early-onset) or later (late-onset) than the estimated reference time 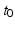 .
.Moreover, since the subject-specific trajectories are affine reparametrizations of an average trajectory, this model can easily be generalized to longitudinal measurements on a Riemannian manifold. The average trajectory may be replaced with a geodesic of the manifold and the subject-specific trajectories will remain geodesics on the manifold. As a matter of fact, longitudinal measurements arising from neuroimaging, neuropsychological tests or clinical examinations may belong to nonlinear spaces. The scores to a neuropsychological test often belong to a bounded interval. Riemannian manifolds offer a very flexible framework which includes the previous examples. The generalization of this statistical model to Riemannian manifold-valued observations could be used either to analyze shapes, cortical thickness measurements or neuropsychological assessment scores. After a proper renormalization, the ADAS-Cog 13 scores belong to the open unit inverval (0, 1) which, equipped with a specific metric, can be seen as a univariate Riemannian manifold. For this metric, the geodesics are logistic curves. The models presented in [2] and [3] do not generalize to manifold-valued data. In [9], Lorenzi et al. used Riemannian manifold techniques to estimate a model of the brain’s normal ageing from healthy individuals T1 MR scans. The model was used to compute a time shift, called morphological age shift, which corresponds to the actual anatomical age of the subject with respect to an estimated average age for healthy subjects. However, the subject-specific time shifts were not estimated as parameters of a statistical model. In [7], Datar et al. generalized a particular linear mixed-effects model to longitudinal shape analysis but the proposed model did not include time shifts to account for the variability in stages of disease progression among the population. Even though the model is used to analyze shapes (given by a set of points), the model is not described in a Riemannian manifold setting.
The work presented herein will generalize the model written above to a Riemannian manifold included in 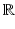 . In Sect. 2, we will introduce our model and we will present two particular cases of this model : the straight lines model and the logistic curves model. We also explain how the parameters of the model are estimated. In Sect. 3, the straight lines model and logistic curves model were used to analyze longitudinal ADAS-Cog and cortical thickness measurements from the ADNI database. We show that the estimated random effects of the model allowed to distinguish between slow versus fast progressing individuals and early versus late-onset individuals.
. In Sect. 2, we will introduce our model and we will present two particular cases of this model : the straight lines model and the logistic curves model. We also explain how the parameters of the model are estimated. In Sect. 3, the straight lines model and logistic curves model were used to analyze longitudinal ADAS-Cog and cortical thickness measurements from the ADNI database. We show that the estimated random effects of the model allowed to distinguish between slow versus fast progressing individuals and early versus late-onset individuals.
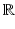 . In Sect. 2, we will introduce our model and we will present two particular cases of this model : the straight lines model and the logistic curves model. We also explain how the parameters of the model are estimated. In Sect. 3, the straight lines model and logistic curves model were used to analyze longitudinal ADAS-Cog and cortical thickness measurements from the ADNI database. We show that the estimated random effects of the model allowed to distinguish between slow versus fast progressing individuals and early versus late-onset individuals.
. In Sect. 2, we will introduce our model and we will present two particular cases of this model : the straight lines model and the logistic curves model. We also explain how the parameters of the model are estimated. In Sect. 3, the straight lines model and logistic curves model were used to analyze longitudinal ADAS-Cog and cortical thickness measurements from the ADNI database. We show that the estimated random effects of the model allowed to distinguish between slow versus fast progressing individuals and early versus late-onset individuals.2 A Mixed-Effects Model with Time Reparametrization for Manifold-Valued Observations
2.1 Model Description
Let us assume that we observe p different individuals. For each individual, we have 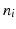 observations, obtained at times
observations, obtained at times 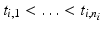 and the observations of the i-th individual are denoted by
and the observations of the i-th individual are denoted by 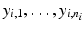 . We assume that each observation
. We assume that each observation 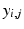 is a point on a one-dimensional Riemannian manifold (M, g) included in
is a point on a one-dimensional Riemannian manifold (M, g) included in 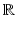 . In addition to this, we assume that the geodesics of M are defined on the entire real line.
. In addition to this, we assume that the geodesics of M are defined on the entire real line.
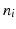 observations, obtained at times
observations, obtained at times 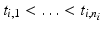 and the observations of the i-th individual are denoted by
and the observations of the i-th individual are denoted by 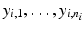 . We assume that each observation
. We assume that each observation 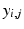 is a point on a one-dimensional Riemannian manifold (M, g) included in
is a point on a one-dimensional Riemannian manifold (M, g) included in 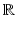 . In addition to this, we assume that the geodesics of M are defined on the entire real line.
. In addition to this, we assume that the geodesics of M are defined on the entire real line.Let 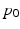 be a point in M,
be a point in M, 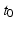 in
in 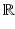 and
and 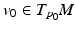 , a tangent vector to M at the point
, a tangent vector to M at the point 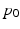 . The triplet
. The triplet 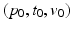 allows to define an average trajectory
allows to define an average trajectory 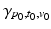 , the geodesic of M which passes through the point
, the geodesic of M which passes through the point 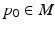 at time
at time 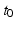 and with the velocity
and with the velocity 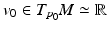 . This average trajectory summarises the progression of all the individuals and could be interpreted as the evolution of an “average subject”. While the average subject passes through the point
. This average trajectory summarises the progression of all the individuals and could be interpreted as the evolution of an “average subject”. While the average subject passes through the point 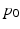 at time
at time 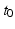 with the velocity
with the velocity 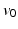 , we assume that the trajectory of the i-th subject is the geodesic
, we assume that the trajectory of the i-th subject is the geodesic 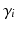 which passes through the point
which passes through the point 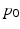 at time
at time 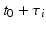 with velocity
with velocity 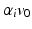 . The parameters
. The parameters 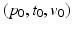 will be the fixed effects of the model whereas
will be the fixed effects of the model whereas 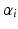 and
and 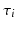 will be the random effects of the model. The point
will be the random effects of the model. The point 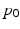 in M can be understood as an observation point. A simplistic interpretation of the role played by
in M can be understood as an observation point. A simplistic interpretation of the role played by 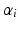 and
and 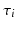 is the following : an observer standing at the point
is the following : an observer standing at the point 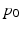 in M and aware that the average subject passes through the point at the time
in M and aware that the average subject passes through the point at the time 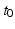 , with velocity
, with velocity 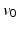 , will be able to tell whether the i-th subject passes through this point earlier or later than the average subject and whether he passes faster or slower. More precisely,
, will be able to tell whether the i-th subject passes through this point earlier or later than the average subject and whether he passes faster or slower. More precisely, 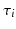 is a time shift which will provide an information on whether the progression of the i-th trajectory is ahead of the average trajectory or not and
is a time shift which will provide an information on whether the progression of the i-th trajectory is ahead of the average trajectory or not and 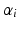 provides the information on whether the i-th subject is evolving faster or slower than the average subject. As a consequence, the random effects
provides the information on whether the i-th subject is evolving faster or slower than the average subject. As a consequence, the random effects 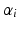 and
and 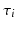 take into account the fact that two different subjects may be at very different stages of disease progression and allow for inter-subjects comparaisons. The description above makes the assumption that every subject-specific trajectory of disease progression will eventually reach a common value
take into account the fact that two different subjects may be at very different stages of disease progression and allow for inter-subjects comparaisons. The description above makes the assumption that every subject-specific trajectory of disease progression will eventually reach a common value 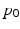 . This assumption does not make sense in a higher-dimensional Riemannian manifold. In order to generalize the proposed model to a higher-dimensional setting, one would need to add another random effect, associated to the fixed effect
. This assumption does not make sense in a higher-dimensional Riemannian manifold. In order to generalize the proposed model to a higher-dimensional setting, one would need to add another random effect, associated to the fixed effect 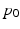 .
.
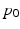 be a point in M,
be a point in M, 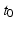 in
in 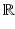 and
and 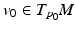 , a tangent vector to M at the point
, a tangent vector to M at the point 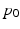 . The triplet
. The triplet 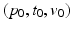 allows to define an average trajectory
allows to define an average trajectory 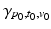 , the geodesic of M which passes through the point
, the geodesic of M which passes through the point 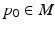 at time
at time 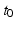 and with the velocity
and with the velocity 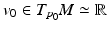 . This average trajectory summarises the progression of all the individuals and could be interpreted as the evolution of an “average subject”. While the average subject passes through the point
. This average trajectory summarises the progression of all the individuals and could be interpreted as the evolution of an “average subject”. While the average subject passes through the point 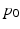 at time
at time 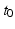 with the velocity
with the velocity 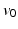 , we assume that the trajectory of the i-th subject is the geodesic
, we assume that the trajectory of the i-th subject is the geodesic 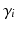 which passes through the point
which passes through the point 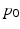 at time
at time 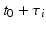 with velocity
with velocity 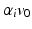 . The parameters
. The parameters 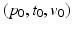 will be the fixed effects of the model whereas
will be the fixed effects of the model whereas 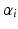 and
and 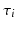 will be the random effects of the model. The point
will be the random effects of the model. The point 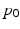 in M can be understood as an observation point. A simplistic interpretation of the role played by
in M can be understood as an observation point. A simplistic interpretation of the role played by 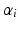 and
and 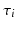 is the following : an observer standing at the point
is the following : an observer standing at the point 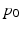 in M and aware that the average subject passes through the point at the time
in M and aware that the average subject passes through the point at the time 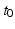 , with velocity
, with velocity 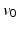 , will be able to tell whether the i-th subject passes through this point earlier or later than the average subject and whether he passes faster or slower. More precisely,
, will be able to tell whether the i-th subject passes through this point earlier or later than the average subject and whether he passes faster or slower. More precisely, 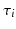 is a time shift which will provide an information on whether the progression of the i-th trajectory is ahead of the average trajectory or not and
is a time shift which will provide an information on whether the progression of the i-th trajectory is ahead of the average trajectory or not and 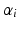 provides the information on whether the i-th subject is evolving faster or slower than the average subject. As a consequence, the random effects
provides the information on whether the i-th subject is evolving faster or slower than the average subject. As a consequence, the random effects 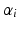 and
and 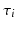 take into account the fact that two different subjects may be at very different stages of disease progression and allow for inter-subjects comparaisons. The description above makes the assumption that every subject-specific trajectory of disease progression will eventually reach a common value
take into account the fact that two different subjects may be at very different stages of disease progression and allow for inter-subjects comparaisons. The description above makes the assumption that every subject-specific trajectory of disease progression will eventually reach a common value 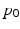 . This assumption does not make sense in a higher-dimensional Riemannian manifold. In order to generalize the proposed model to a higher-dimensional setting, one would need to add another random effect, associated to the fixed effect
. This assumption does not make sense in a higher-dimensional Riemannian manifold. In order to generalize the proposed model to a higher-dimensional setting, one would need to add another random effect, associated to the fixed effect 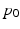 .
.Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree




