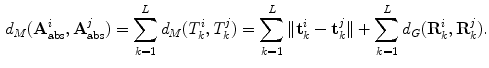consists of 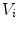 vertices
vertices 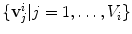 and
and 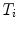 triangles.
triangles.
Further prior knowledge can be encoded into the surface meshes by labelling the individual triangles. An example is given in Fig. 1a. This labelling allows to easily derive certain vertebra characteristics directly from the mesh, e.g., distance between vertebral body surfaces. Finally, important anatomical landmarks can be annotated in the mesh as shown in Fig. 1b. As both surface labelling and landmark setting only need to be done once during model generation, manual annotation is typically done.
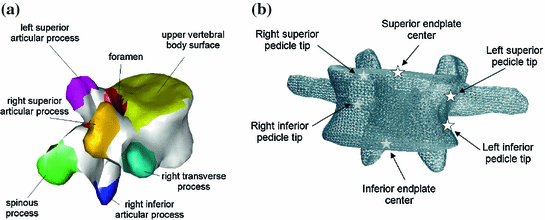

Fig. 1
Illustration of additional prior knowledge encoded into the shape models, a Labelling of anatomical regions. b Annotated anatomical landmarks
The surface descriptions can be embedded into a multi-resolution representation with different levels of complexity. In [20], three levels of polygonal mesh catalogues were created to speed up processing and allow for optimal convergence using a coarse-to-fine strategy during registration.
2.2 Statistical Shape Modelling
From the initial vertebra surface representations, we can build statistical vertebra shape models by adapting the surfaces to a set of images. During patient individualization, we carefully preserve the established vertex distribution of the generated vertebra surface representation. By using the adaptation algorithm from Chapter 5, the topology remains unchanged and the vertex distribution is constrained to be similar to the respective reference mesh, so that the 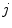 th landmark of the
th landmark of the 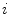 th mesh lies at approximately the same anatomical position for all cases. After segmentation of all vertebrae in a set of training images, a Procrustes co-registration is performed and finally a point distribution model can be obtained. In the following, we keep however only the mean surface models
th mesh lies at approximately the same anatomical position for all cases. After segmentation of all vertebrae in a set of training images, a Procrustes co-registration is performed and finally a point distribution model can be obtained. In the following, we keep however only the mean surface models 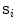 for each vertebra. Thus, the overall geometrical spine model can be expressed as
for each vertebra. Thus, the overall geometrical spine model can be expressed as 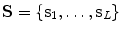 with
with 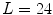 if all vertebrae are considered.
if all vertebrae are considered.
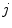 th landmark of the
th landmark of the 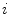 th mesh lies at approximately the same anatomical position for all cases. After segmentation of all vertebrae in a set of training images, a Procrustes co-registration is performed and finally a point distribution model can be obtained. In the following, we keep however only the mean surface models
th mesh lies at approximately the same anatomical position for all cases. After segmentation of all vertebrae in a set of training images, a Procrustes co-registration is performed and finally a point distribution model can be obtained. In the following, we keep however only the mean surface models 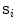 for each vertebra. Thus, the overall geometrical spine model can be expressed as
for each vertebra. Thus, the overall geometrical spine model can be expressed as 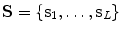 with
with 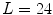 if all vertebrae are considered.
if all vertebrae are considered.2.3 Vertebra Coordinate System
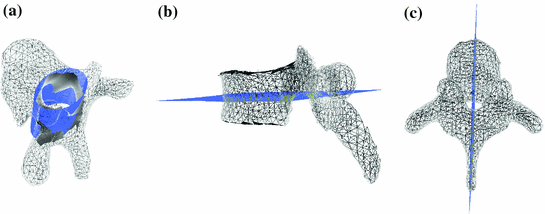
In addition to the surface representation, each vertebra model carries its own local vertebra coordinate system (VCS). This allows to express relative location and orientation of the individual vertebrae. In order to have similar definition of the VCS for the individual vertebrae along the spine, a VCS is typically defined by invariant object characteristics and different definitions have been proposed. In [23], we derived the VCS of all vertebra from the surface mesh representation including the labelling of anatomical regions (see Fig. 1a). For the vertebrae C3 to L5, the VCS was defined in the same way since these vertebrae show similar shape characteristics. The definition of the VCS was based on three object-related simplified representations: a cylinder fit to the vertebral foramen, the middle plane of the upper and lower vertebral body surfaces, and the sagittal symmetry plane of the vertebra (see Fig. 2). The definition of the VCS was as follows: The origin of the VCS was located in the mid-vertebral plane at the centre of the vertebral foramen. The normal vector of the middle plane defined the 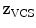 -axis, the
-axis, the 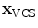 -axis was defined by the orthogonal component of the normal vector of the symmetry plane and the
-axis was defined by the orthogonal component of the normal vector of the symmetry plane and the 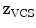 -axis. The cross product of
-axis. The cross product of 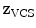 -axis and
-axis and 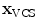 -axis resulted in the
-axis resulted in the 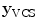 -axis [23]. For the unique definition of the VCS for C1 and C2, other characteristics were chosen. A vertex subset was chosen containing the vertices belonging to the inferior articular faces and the anterior tubercle. The axes of the specific VCSs are given by the covariance analysis of the subset. The eigenvector corresponding to the largest eigenvalue of the covariance matrix points to the lateral direction defining the
-axis [23]. For the unique definition of the VCS for C1 and C2, other characteristics were chosen. A vertex subset was chosen containing the vertices belonging to the inferior articular faces and the anterior tubercle. The axes of the specific VCSs are given by the covariance analysis of the subset. The eigenvector corresponding to the largest eigenvalue of the covariance matrix points to the lateral direction defining the 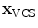 -axis, the second eigenvector pointing towards the anterior tubercle gives the
-axis, the second eigenvector pointing towards the anterior tubercle gives the 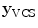 -axis, and finally, the third eigenvector points towards the direction of the spinal canal denoting the
-axis, and finally, the third eigenvector points towards the direction of the spinal canal denoting the 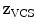 -axis. The barycentre of the subset defines the origin of the VCS.
-axis. The barycentre of the subset defines the origin of the VCS.
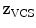 -axis, the
-axis, the 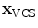 -axis was defined by the orthogonal component of the normal vector of the symmetry plane and the
-axis was defined by the orthogonal component of the normal vector of the symmetry plane and the 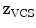 -axis. The cross product of
-axis. The cross product of 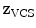 -axis and
-axis and 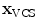 -axis resulted in the
-axis resulted in the 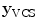 -axis [23]. For the unique definition of the VCS for C1 and C2, other characteristics were chosen. A vertex subset was chosen containing the vertices belonging to the inferior articular faces and the anterior tubercle. The axes of the specific VCSs are given by the covariance analysis of the subset. The eigenvector corresponding to the largest eigenvalue of the covariance matrix points to the lateral direction defining the
-axis [23]. For the unique definition of the VCS for C1 and C2, other characteristics were chosen. A vertex subset was chosen containing the vertices belonging to the inferior articular faces and the anterior tubercle. The axes of the specific VCSs are given by the covariance analysis of the subset. The eigenvector corresponding to the largest eigenvalue of the covariance matrix points to the lateral direction defining the 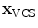 -axis, the second eigenvector pointing towards the anterior tubercle gives the
-axis, the second eigenvector pointing towards the anterior tubercle gives the 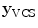 -axis, and finally, the third eigenvector points towards the direction of the spinal canal denoting the
-axis, and finally, the third eigenvector points towards the direction of the spinal canal denoting the 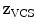 -axis. The barycentre of the subset defines the origin of the VCS.
-axis. The barycentre of the subset defines the origin of the VCS.
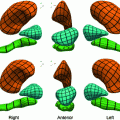
Fig. 2
Invariant features of vertebrae used to define a VCS: Cylinder fit to vertebral foramen (a), middle plane of upper and lower vertebral body surface (b) as well as sagittal symmetry plane (c)
2.4 Gradient Model
For vertebra detection, we further created generalised Hough transform models of each vertebra. The generalised Hough transform (GHT) [6] is a robust and powerful method to detect arbitrary shapes in an image undergoing geometric transformations. During GHT learning, description of the shape is encoded into a reference table also called R-table. Its entries are vectors pointing from the shape boundary to a reference point being commonly the gravity centre of the shape. During detection, the gradient orientation is measured at each edge voxel of the new image yielding an index for an entry of the R-table. Then, the positions pointed by all vectors under this entry are incremented in an accumulator array. Finally, the shape is given by the highest peak in the accumulator array. Usually, the GHT is trained for one single reference shape of an object class. In addition to specific GHT models for C1 to L5 we build general cervical, thoracic and lumbar GHT models. The general models can be applied if the field of view of the available image is unknown while the more specific models can be used if some indication for a certain area of the spine is given.


Fig. 3
Gradient model representation of sixth thoracic vertebra in axial and sagittal view showing the model points. The model has been created from ten samples
For model generation, shape models adapted to a set of training images are superimposed based on the VCSs and the obtained aligned shapes are used to build up the R-table. Note that the orientation is not considered during GHT learning since all shapes were aligned via the respective VCS. In contrast to the above mentioned shape models, the GHT models do not only contain shape information but also gradient information. A gradient model for the sixth thoracic vertebra can be seen in Fig. 3. For more details about the gradient models, we refer to [24].
2.5 Appearance Model
Vertebra appearance models in this case are represented as average intensity volumes inside a bounding box around each vertebra without explicitly modeling the vertebra’s shape. The information covered in the model about expected appearance in the direct neighbourhood of each vertebra can be used to identify vertebrae in an image by comparing the similarity between model and image content. For model generation, shape models need to be adapted to a set of training images. Mean intensity volumes are then generated by aligning volumes around corresponding vertebrae and averaging the intensity values. Alignment is performed by registration of the vertebra shape models to their respective model space. The obtained transformations can then be applied on the respective voxel positions. Location and pose of the object in the volumes are expressed by the VCSs of the mean vertebra models that were used for alignment. Exemplarily, the appearance model of the sixth thoracic vertebra is shown in Fig. 4. Inter-patient variability becomes obvious by blurry object boundaries whereas the particular objects are still clearly delimited. More details can be found in [24].
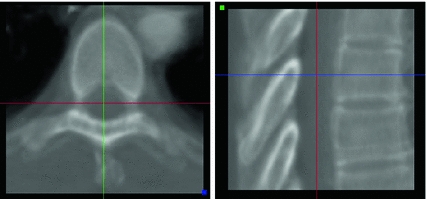

Fig. 4
Appearance model of sixth thoracic vertebra in axial and sagittal view generated from ten training images. The volume has a sample distance of 0.5 mm in each direction. The cross gives the origin of the VCS
3 Articulated Models
In the previous section, each vertebra has been represented seperately by a set of detailed models. However, in order to model the overall constellation of the spine, the articulation between the individual vertebrae has to be considered. In this section, we first introduce a general representation of the articulated spine model in Sect. 3.1. Based on this representation, statistical modeling of the spine can be done and two different methods are proposed in Sects. 3.2 and 3.3. In each case, it is furthermore shown how the articulated model can be individualized to a new patient.
3.1 Model Definition
As defined in Sect. 2, the geometric model of the spine is defined as 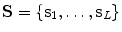 consisting of an interconnection of
consisting of an interconnection of 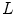 objects. Each local shape
objects. Each local shape 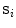 is represented as a triangulated mesh including a VCS to rigidly register each object to its upper neighbor.
is represented as a triangulated mesh including a VCS to rigidly register each object to its upper neighbor.
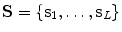 consisting of an interconnection of
consisting of an interconnection of 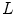 objects. Each local shape
objects. Each local shape 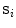 is represented as a triangulated mesh including a VCS to rigidly register each object to its upper neighbor.
is represented as a triangulated mesh including a VCS to rigidly register each object to its upper neighbor.The resulting rigid transforms are stored for each inter-object link. Hence, an articulated deformable model (ADM) is represented by a series of local inter-object rigid transformations 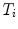 (translation and rotation) between neighbouring vertebrae resulting in
(translation and rotation) between neighbouring vertebrae resulting in
![$$\begin{aligned} {\mathbf {A}}=[T_1, T_2, \ldots , T_{L-1}]\,. \end{aligned}$$](/wp-content/uploads/2016/10/A312883_1_En_11_Chapter_Equ1.gif)
While 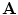 covers the individual inter-object transformations, the global shape of the spine shape can be expressed by converting
covers the individual inter-object transformations, the global shape of the spine shape can be expressed by converting 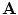 into an absolute representation
into an absolute representation
![$$\begin{aligned} {\mathbf {A}}_{\mathrm {abs}}=[T_1, T_1 \circ T_2, \ldots , T_1 \circ T_2 \circ \ldots \circ T_{L-1}] \end{aligned}$$](/wp-content/uploads/2016/10/A312883_1_En_11_Chapter_Equ2.gif)
using recursive compositions. The respective transformations are expressed in the VCS of the lower object.
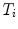 (translation and rotation) between neighbouring vertebrae resulting in
(translation and rotation) between neighbouring vertebrae resulting in![$$\begin{aligned} {\mathbf {A}}=[T_1, T_2, \ldots , T_{L-1}]\,. \end{aligned}$$](/wp-content/uploads/2016/10/A312883_1_En_11_Chapter_Equ1.gif)
(1)
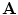 covers the individual inter-object transformations, the global shape of the spine shape can be expressed by converting
covers the individual inter-object transformations, the global shape of the spine shape can be expressed by converting 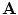 into an absolute representation
into an absolute representation![$$\begin{aligned} {\mathbf {A}}_{\mathrm {abs}}=[T_1, T_1 \circ T_2, \ldots , T_1 \circ T_2 \circ \ldots \circ T_{L-1}] \end{aligned}$$](/wp-content/uploads/2016/10/A312883_1_En_11_Chapter_Equ2.gif)
(2)
The relationship between the shape model 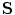 and the ADM is that the articulation vector
and the ADM is that the articulation vector 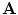 controls the position and orientation of the object constellation
controls the position and orientation of the object constellation 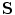 . The ADM can achieve deformation by modifying the vector of rigid transformations, which taken in its entirety, performs a global deformation of the spine [22].
. The ADM can achieve deformation by modifying the vector of rigid transformations, which taken in its entirety, performs a global deformation of the spine [22].
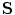 and the ADM is that the articulation vector
and the ADM is that the articulation vector 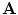 controls the position and orientation of the object constellation
controls the position and orientation of the object constellation 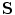 . The ADM can achieve deformation by modifying the vector of rigid transformations, which taken in its entirety, performs a global deformation of the spine [22].
. The ADM can achieve deformation by modifying the vector of rigid transformations, which taken in its entirety, performs a global deformation of the spine [22].The rigid transformations are the combination of a rotation matrix 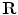 and a translation vector
and a translation vector 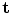 , while scaling is not considered. We formulate the rigid transformation
, while scaling is not considered. We formulate the rigid transformation 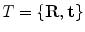 of a triangular mesh model as
of a triangular mesh model as 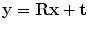 where
where 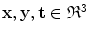 . Composition is given by
. Composition is given by 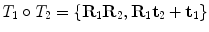 .
.
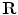 and a translation vector
and a translation vector 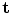 , while scaling is not considered. We formulate the rigid transformation
, while scaling is not considered. We formulate the rigid transformation 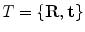 of a triangular mesh model as
of a triangular mesh model as 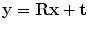 where
where 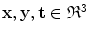 . Composition is given by
. Composition is given by 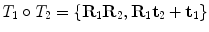 .
.Alternatively, a rigid transformation can be fully described by an axis of rotation supported by a unit vector 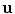 and an angle of rotation
and an angle of rotation 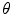 . The rotation vector
. The rotation vector 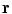 is defined as the product of
is defined as the product of 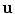 and
and 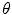 . Thus, a rigid transformation can be expressed as
. Thus, a rigid transformation can be expressed as 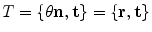 . The conversion between the two representations is simple, since the rotation vector can be converted into a rotation matrix using Rodrigues’ formula (see Appendix for more details).
. The conversion between the two representations is simple, since the rotation vector can be converted into a rotation matrix using Rodrigues’ formula (see Appendix for more details).
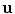 and an angle of rotation
and an angle of rotation 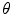 . The rotation vector
. The rotation vector 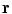 is defined as the product of
is defined as the product of 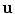 and
and 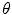 . Thus, a rigid transformation can be expressed as
. Thus, a rigid transformation can be expressed as 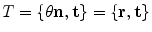 . The conversion between the two representations is simple, since the rotation vector can be converted into a rotation matrix using Rodrigues’ formula (see Appendix for more details).
. The conversion between the two representations is simple, since the rotation vector can be converted into a rotation matrix using Rodrigues’ formula (see Appendix for more details).3.2 Linear Model
3.2.1 Model Generation
In order to capture variations of the spine curve, statistics need to be applied on the articulated model. As defined in the previous section, the spine is expressed as a vector of rigid transformation and there is no addition or scalar multiplication defined between them. Thus, as the representation no longer belongs to a vector space, conventional statistics can not be applied. However, rigid transformations belong to a Riemannian manifold and Riemannian geometry concepts can be efficiently applied to generalize statistical notions to articulated shape models of the spine. The mathematical framework described in the following has been introduced by Boisvert et al. and explained, e.g., in [8–10].
Following the statistics for Riemannian manifolds, the generalization of the usual mean called the Fr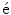 chet mean can be defined for a given distance measure as the element
chet mean can be defined for a given distance measure as the element 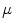 that minimizes the sum of the distances with a set of elements
that minimizes the sum of the distances with a set of elements 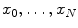 of the same manifold
of the same manifold 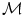 :
:
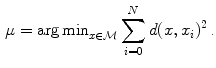
Since the mean is given as a minimization, the gradient descent method can be performed on the summation obtaining
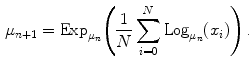
The functions Exp and Log are respectively the exponential map and the log map associated with the distance 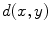 . The exponential map projects an element of the tangent plane on the manifold
. The exponential map projects an element of the tangent plane on the manifold 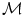 and the log map is the inverse function.
and the log map is the inverse function.
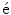 chet mean can be defined for a given distance measure as the element
chet mean can be defined for a given distance measure as the element 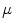 that minimizes the sum of the distances with a set of elements
that minimizes the sum of the distances with a set of elements 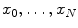 of the same manifold
of the same manifold 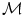 :
: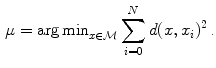
(3)
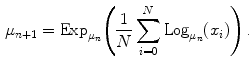
(4)
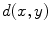 . The exponential map projects an element of the tangent plane on the manifold
. The exponential map projects an element of the tangent plane on the manifold 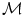 and the log map is the inverse function.
and the log map is the inverse function.The intuitive generalization of the variance is the expectation of the squared distance between the elements 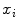 :
:
![$$\begin{aligned} \sigma ^2 = E[d(\mu , x)^2] = \frac{1}{N}\sum _{i=0}^{N}{d(\mu , x_i)^2}. \end{aligned}$$](/wp-content/uploads/2016/10/A312883_1_En_11_Chapter_Equ5.gif)
The covariance is usually defined as the expectation of the matricial product of the vectors from the mean to the elements on which the covariance is computed. The expression for Riemannian manifolds can thus be given by using again the Log map [8]:
![$$\begin{aligned} \varSigma _{xx} = E[{\mathrm {Log}}(\mu ^{-1}x)^T{\mathrm {Log}}(\mu ^{-1}x)] = \frac{1}{N}\sum _{i=0}^{N}{\mathrm {Log}}_\mu (x){\mathrm {Log}}_\mu (x)^T. \end{aligned}$$](/wp-content/uploads/2016/10/A312883_1_En_11_Chapter_Equ6.gif)
To use the Riemannian framework defined by Eqs. 3–6, a suitable distance needs to be defined first to find the structure of the geodesics on the manifold. For this purpose, we rely on the representation of transformation as a rotation vector as defined in Sect. 3.1. With this representation, the left-invariant distance definition between two rigid transformations can be defined [9]:
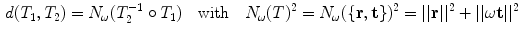
where 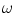 is used to weight the relative effect of rotation and translation,
is used to weight the relative effect of rotation and translation, 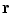 is the rotation vector, and
is the rotation vector, and 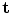 the translation vector. An appropriate value for the weight factor
the translation vector. An appropriate value for the weight factor 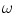 in the case of the spine is found to be 0.05 [8].
in the case of the spine is found to be 0.05 [8].
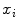 :
:![$$\begin{aligned} \sigma ^2 = E[d(\mu , x)^2] = \frac{1}{N}\sum _{i=0}^{N}{d(\mu , x_i)^2}. \end{aligned}$$](/wp-content/uploads/2016/10/A312883_1_En_11_Chapter_Equ5.gif)
(5)
![$$\begin{aligned} \varSigma _{xx} = E[{\mathrm {Log}}(\mu ^{-1}x)^T{\mathrm {Log}}(\mu ^{-1}x)] = \frac{1}{N}\sum _{i=0}^{N}{\mathrm {Log}}_\mu (x){\mathrm {Log}}_\mu (x)^T. \end{aligned}$$](/wp-content/uploads/2016/10/A312883_1_En_11_Chapter_Equ6.gif)
(6)
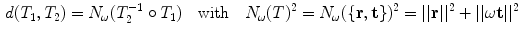
(7)
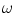 is used to weight the relative effect of rotation and translation,
is used to weight the relative effect of rotation and translation, 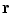 is the rotation vector, and
is the rotation vector, and 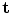 the translation vector. An appropriate value for the weight factor
the translation vector. An appropriate value for the weight factor 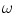 in the case of the spine is found to be 0.05 [8].
in the case of the spine is found to be 0.05 [8].
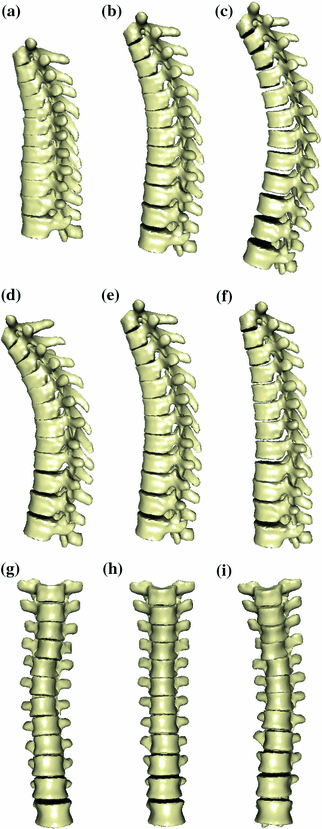
Fig. 5
First, second and third eigenmode of the statistical model on transformation between the local coordinate systems defined on the 12 thoracic vertebrae. Each row shows the mean transformation model 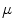 and the mean plus a particular eigenmode weighted by
and the mean plus a particular eigenmode weighted by 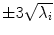 with
with 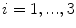 . The resulting transformations are applied to mean shape models based on 18 patient data sets, a
. The resulting transformations are applied to mean shape models based on 18 patient data sets, a 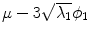 , b Mean
, b Mean 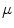 , c
, c 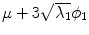 , d
, d 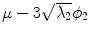 , e Mean
, e Mean 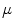 , f
, f 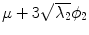 , g
, g 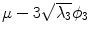 , h Mean
, h Mean 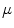 , i
, i 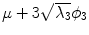
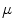 and the mean plus a particular eigenmode weighted by
and the mean plus a particular eigenmode weighted by 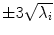 with
with 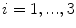 . The resulting transformations are applied to mean shape models based on 18 patient data sets, a
. The resulting transformations are applied to mean shape models based on 18 patient data sets, a 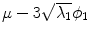 , b Mean
, b Mean 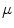 , c
, c 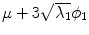 , d
, d 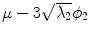 , e Mean
, e Mean 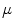 , f
, f 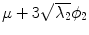 , g
, g 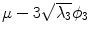 , h Mean
, h Mean 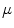 , i
, i 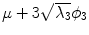
Finally, exponential and logarithmic map associated with the defined distance are the conversions between the rotation vector and the rotation matrix combined with a scaled version of the translation vector [8]
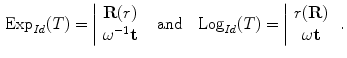
Given the articulated model of the spine is expressed as the multivariate vector ![$${\mathbf {A}}^T=[T_1, T_2, \ldots , T_L]^T$$](/wp-content/uploads/2016/10/A312883_1_En_11_Chapter_IEq63.gif) from Eq. 1 of
from Eq. 1 of 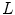 rigid transformations, we obtain for the mean and the covariance
rigid transformations, we obtain for the mean and the covariance
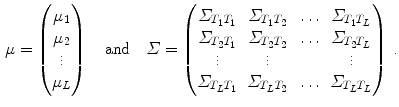
With Eq. 9, the formulation for the linear statistical spine model is given. In order to reduce the dimensionality of the model, principal component analysis (PCA) can be performed on the covariance matrix. As an example, Fig. 5 shows the first three eigenmodes after applying PCA to the statistics of transformations between the 12 thoracic vertebrae obtained from 18 patients.
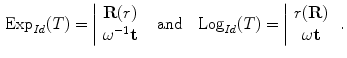
(8)
![$${\mathbf {A}}^T=[T_1, T_2, \ldots , T_L]^T$$](/wp-content/uploads/2016/10/A312883_1_En_11_Chapter_IEq63.gif) from Eq. 1 of
from Eq. 1 of  rigid transformations, we obtain for the mean and the covariance
rigid transformations, we obtain for the mean and the covariance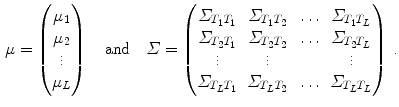
(9)
3.2.2 Model Adaption
The statistical spine model can be used to support image segmentation. It allows to consider the object constellation during segmentation instead of separate segmentation of the individual vertebrae, thus going from single object to multi-object segmentation. Such a framework has been presented in [25] for the segmentation of the spine in CT. Its general idea is to follow a two-scale adaptation approach. During a global adaptation step, the individual vertebrae are at first roughly positioned in the image. Afterwards, exact segmentation of the vertebrae is achieved by adaptation of the respective vertebra shape models. In this section, we focus on the adaptation of the global model, while details for deformable surface mesh adaptation are basically explained earlier in Chap. 5.
The idea of global adaptation is to determine the inter-object transformations 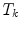 by minimizing an energy term
by minimizing an energy term 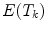 where an external energy
where an external energy 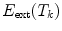 drives the vertebrae towards image features, while an internal energy
drives the vertebrae towards image features, while an internal energy 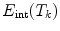 restricts attraction to a former learned constellation model
restricts attraction to a former learned constellation model
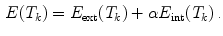
The parameter 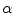 controls the trade-off between both energy terms which are explained in the following.
controls the trade-off between both energy terms which are explained in the following.
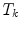 by minimizing an energy term
by minimizing an energy term 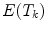 where an external energy
where an external energy 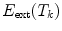 drives the vertebrae towards image features, while an internal energy
drives the vertebrae towards image features, while an internal energy 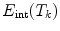 restricts attraction to a former learned constellation model
restricts attraction to a former learned constellation model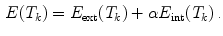
(10)
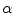 controls the trade-off between both energy terms which are explained in the following.
controls the trade-off between both energy terms which are explained in the following.The external energy attracts each vertebra towards its corresponding image structures. Thus, we first need to define a feature function such as
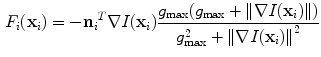
that evaluates for each vertebra independently the match between the vertebra surface mesh and the underlying image structure. The feature function is evaluated for each triangle of the surface mesh at the position of the triangle barycentre 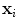 . The image gradient
. The image gradient 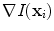 is projected onto the face normal
is projected onto the face normal 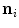 of each triangle and damped by
of each triangle and damped by 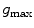 . The feature values of all triangles are summed up providing one value per vertebra for the current position.
. The feature values of all triangles are summed up providing one value per vertebra for the current position.
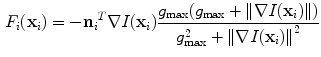
(11)
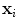 . The image gradient
. The image gradient 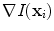 is projected onto the face normal
is projected onto the face normal 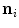 of each triangle and damped by
of each triangle and damped by 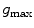 . The feature values of all triangles are summed up providing one value per vertebra for the current position.
. The feature values of all triangles are summed up providing one value per vertebra for the current position.The search for a new vertebra position is performed by testing various discrete locations inside a local neighborhood around a given position. For that purpose, a cartesian grid inside a bounding box around the current estimated vertebra location is defined. In order to not only cope with translations but also rotations, the original object is rotated in discrete steps around all axes obtaining 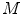 rotation matrices
rotation matrices 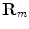 . At each of the
. At each of the 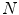 grid positions, the feature function from Eq. 11 is evaluated for the corresponding surface mesh translated by
grid positions, the feature function from Eq. 11 is evaluated for the corresponding surface mesh translated by 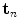 as well as its
as well as its 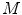 rotated versions. Due to the frequent presence of local minima, the exhaustive search of transformation parameters is preferred to other optimization strategies. It has to be noted again that this search aims at finding a new vertebra position while the original surface model is not deformed yet.
rotated versions. Due to the frequent presence of local minima, the exhaustive search of transformation parameters is preferred to other optimization strategies. It has to be noted again that this search aims at finding a new vertebra position while the original surface model is not deformed yet.
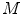 rotation matrices
rotation matrices 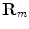 . At each of the
. At each of the 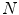 grid positions, the feature function from Eq. 11 is evaluated for the corresponding surface mesh translated by
grid positions, the feature function from Eq. 11 is evaluated for the corresponding surface mesh translated by 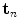 as well as its
as well as its 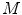 rotated versions. Due to the frequent presence of local minima, the exhaustive search of transformation parameters is preferred to other optimization strategies. It has to be noted again that this search aims at finding a new vertebra position while the original surface model is not deformed yet.
rotated versions. Due to the frequent presence of local minima, the exhaustive search of transformation parameters is preferred to other optimization strategies. It has to be noted again that this search aims at finding a new vertebra position while the original surface model is not deformed yet.The transformation resulting in the highest feature strength determines the new position of the object:
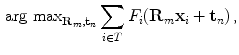
where 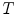 is the number of triangles per mesh.
is the number of triangles per mesh.
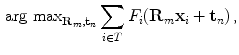
(12)
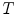 is the number of triangles per mesh.
is the number of triangles per mesh.After finding the most promising positions for a pair of neighboring objects 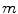 and
and 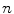 , we can define the global external energy for the corresponding
, we can define the global external energy for the corresponding 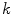 th transformation using the distance measure between transformations as introduced in Eq. 7:
th transformation using the distance measure between transformations as introduced in Eq. 7:
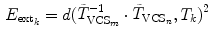
where 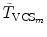 and
and 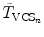 are the transformations of the corresponding VCSs at the new positions to the world coordinate system. Thus,
are the transformations of the corresponding VCSs at the new positions to the world coordinate system. Thus, 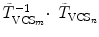 gives the transformation between the corresponding VCSs.
gives the transformation between the corresponding VCSs.
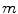 and
and 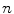 , we can define the global external energy for the corresponding
, we can define the global external energy for the corresponding 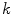 th transformation using the distance measure between transformations as introduced in Eq. 7:
th transformation using the distance measure between transformations as introduced in Eq. 7: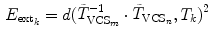
(13)
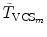 and
and 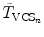 are the transformations of the corresponding VCSs at the new positions to the world coordinate system. Thus,
are the transformations of the corresponding VCSs at the new positions to the world coordinate system. Thus, 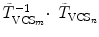 gives the transformation between the corresponding VCSs.
gives the transformation between the corresponding VCSs.Driving the model towards high image features as performed by the external energy is restricted by the internal energy to prevent false attraction. The internal energy preserves similarity of the ensemble towards an earlier learned constellation model. This is expressed by defining for each transformation 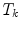
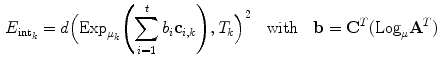
where the matrix of the individual eigenvectors 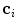 is denoted as
is denoted as 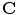 and
and 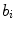 is the coordinate of the weight vector
is the coordinate of the weight vector 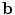 associated with the
associated with the 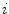 th principal component. The internal energy penalizes differences between the model and the current constellation. The closest constellation to the model is determined by projecting the given constellation
th principal component. The internal energy penalizes differences between the model and the current constellation. The closest constellation to the model is determined by projecting the given constellation 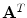 in the sub-space defined by the principal components.
in the sub-space defined by the principal components.
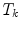
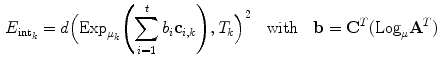
(14)
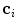 is denoted as
is denoted as 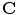 and
and 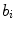 is the coordinate of the weight vector
is the coordinate of the weight vector 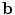 associated with the
associated with the 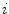 th principal component. The internal energy penalizes differences between the model and the current constellation. The closest constellation to the model is determined by projecting the given constellation
th principal component. The internal energy penalizes differences between the model and the current constellation. The closest constellation to the model is determined by projecting the given constellation 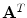 in the sub-space defined by the principal components.
in the sub-space defined by the principal components.After calculating the respective energy terms, the final transformations 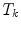 between the individual objects are determined by minimizing
between the individual objects are determined by minimizing
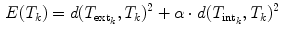
for each object separately. The transformations 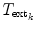 and
and 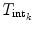 are obtained from the external and internal energy, respectively. The final transformation
are obtained from the external and internal energy, respectively. The final transformation 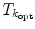 is found using a Downhill-Simplex optimizer. As the representation of the ensemble as a consecution of rigid transformations requires a reference VCS, the vertebra with the highest feature strength is taken as the reference in each iteration.
is found using a Downhill-Simplex optimizer. As the representation of the ensemble as a consecution of rigid transformations requires a reference VCS, the vertebra with the highest feature strength is taken as the reference in each iteration.
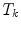 between the individual objects are determined by minimizing
between the individual objects are determined by minimizing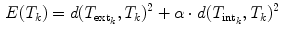
(15)
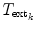 and
and 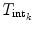 are obtained from the external and internal energy, respectively. The final transformation
are obtained from the external and internal energy, respectively. The final transformation 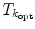 is found using a Downhill-Simplex optimizer. As the representation of the ensemble as a consecution of rigid transformations requires a reference VCS, the vertebra with the highest feature strength is taken as the reference in each iteration.
is found using a Downhill-Simplex optimizer. As the representation of the ensemble as a consecution of rigid transformations requires a reference VCS, the vertebra with the highest feature strength is taken as the reference in each iteration.After positioning the vertebra models using the global model adaptation, a local non-rigid free-form deformation similar to Chap. 5 of the individual surface meshes can be carried out. In order to improve segmentation, all vertebrae are adapted simultaneously with the individual shapes interacting on each other to prevent misadaptations. This has been realized in [25] by introducing a collision detection into feature search and decreasing the feature strength the deeper a target point lies inside another mesh.
3.3 Manifold Embedding
3.3.1 Model Generation
As an alternative to the linear statistical model proposed in the previous section, low-dimensional manifold embedding of the articulated model has been proposed in [20, 21].
For non-linear embedding, we rely on the absolute vector representation ![$${\mathbf {A}}_{\mathrm {abs}}=[T_1, T_1 \circ T_2, \ldots , T_1 \circ T_2 \circ \ldots \circ T_{L-1}]$$](/wp-content/uploads/2016/10/A312883_1_En_11_Chapter_IEq97.gif) as given in Eq. 2. Let us now consider
as given in Eq. 2. Let us now consider 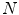 articulated shape models expressed by the feature vectors
articulated shape models expressed by the feature vectors 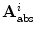 , of dimensionality
, of dimensionality 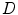 . The aim is to create a low-dimensional manifold consisting of
. The aim is to create a low-dimensional manifold consisting of 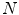 points
points ![$${\mathbf {Y}}_{i}, {\mathbf {Y}}_{i}\in \mathfrak {R}^{d}, i\in [1,N]$$](/wp-content/uploads/2016/10/A312883_1_En_11_Chapter_IEq102.gif) where
where 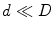 based on [35]. In such a framework, if an adequate number of data points is available, then the underlying manifold
based on [35]. In such a framework, if an adequate number of data points is available, then the underlying manifold 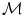 is considered to be “well-sampled”. Therefore, it can represent the underlying population structure. In the sub-cluster corresponding to a pathological population, each point of the training set and its neighbours would lie within a locally linear patch as illustrated in Fig. 6.
is considered to be “well-sampled”. Therefore, it can represent the underlying population structure. In the sub-cluster corresponding to a pathological population, each point of the training set and its neighbours would lie within a locally linear patch as illustrated in Fig. 6.
![$${\mathbf {A}}_{\mathrm {abs}}=[T_1, T_1 \circ T_2, \ldots , T_1 \circ T_2 \circ \ldots \circ T_{L-1}]$$](/wp-content/uploads/2016/10/A312883_1_En_11_Chapter_IEq97.gif) as given in Eq. 2. Let us now consider
as given in Eq. 2. Let us now consider 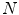 articulated shape models expressed by the feature vectors
articulated shape models expressed by the feature vectors 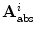 , of dimensionality
, of dimensionality 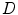 . The aim is to create a low-dimensional manifold consisting of
. The aim is to create a low-dimensional manifold consisting of 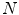 points
points ![$${\mathbf {Y}}_{i}, {\mathbf {Y}}_{i}\in \mathfrak {R}^{d}, i\in [1,N]$$](/wp-content/uploads/2016/10/A312883_1_En_11_Chapter_IEq102.gif) where
where 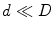 based on [35]. In such a framework, if an adequate number of data points is available, then the underlying manifold
based on [35]. In such a framework, if an adequate number of data points is available, then the underlying manifold 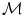 is considered to be “well-sampled”. Therefore, it can represent the underlying population structure. In the sub-cluster corresponding to a pathological population, each point of the training set and its neighbours would lie within a locally linear patch as illustrated in Fig. 6.
is considered to be “well-sampled”. Therefore, it can represent the underlying population structure. In the sub-cluster corresponding to a pathological population, each point of the training set and its neighbours would lie within a locally linear patch as illustrated in Fig. 6.
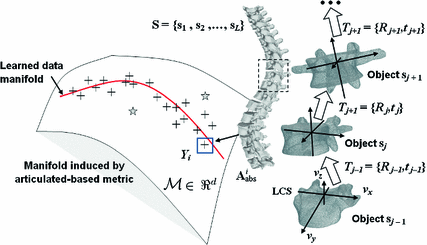
Fig. 6
Representation of inter-vertebral transformations in manifold space
The main limitation of embedding algorithms is the assumption of Euclidean metrics in the ambient space to evaluate similarity between sample points. Thus, similar to Sect. 3.2, a metric in the space of articulated structures is defined that accommodates for anatomical spine variability and adopts the intrinsic nature of the Riemannian manifold geometry allowing us to discern between articulated shape deformations in a topological invariant framework. For each point, the 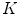 closest neighbours are selected using a distortion metric which is particularly suited for geodesics. The metric
closest neighbours are selected using a distortion metric which is particularly suited for geodesics. The metric 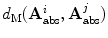 estimates the distance of articulated models
estimates the distance of articulated models 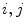 . The distance measure for absolute representations can therefore be expressed as a sum of articulation deviations
. The distance measure for absolute representations can therefore be expressed as a sum of articulation deviations
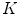 closest neighbours are selected using a distortion metric which is particularly suited for geodesics. The metric
closest neighbours are selected using a distortion metric which is particularly suited for geodesics. The metric 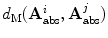 estimates the distance of articulated models
estimates the distance of articulated models 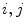 . The distance measure for absolute representations can therefore be expressed as a sum of articulation deviations
. The distance measure for absolute representations can therefore be expressed as a sum of articulation deviations