The relevance of the brainstem to the spinal anatomy is summarized in Fig. 1. The brainstem consists of the midbrain, pons and medulla oblongata; while it lies in the inferior part of the brain, the brainstem is structurally continuous with the spinal cord. Also, surgery planning and simulation of the spine require adequate modeling of critical tissues, the most important of which are spinal nerves, and in the cervical portion of the spine, three of these major nerves, the glossopharyngeal (IX), vagus (X) and accessory nerves (XI) run near spinal nerves, while nerve XI has both a cranial and a spinal portion with roots in the brainstem and spine, as depicted in Fig. 1.
Just as importantly, as seen in Fig. 2, the brainstem is extremely relevant to modeling the neuroanatomy of the skull base. In particular, the brainstem imbeds the nuclei and tracts of ten pairs of cranial nerves, nerves III to XII, and can be thought of as a twenty-legged spider. The olfactory (I) and ocular (II) nerves, emerge from the forebrain anteriorly and superiorly to the brainstem. So far, modeling that is conducive to the minimally supervised segmentation of cranial nerves has been neglected by the computer assisted surgery community.
1.2 Objectives and Clinical Motivation
The long-term clinical objective of this project is to provide a minimally supervised segmentation tool for patient-specific modeling of the brainstem. There are a number of digital atlases of the brain in open source, but these atlases neglect the brainstem: these atlases typically represent the whole brain, with little detail provided on the brainstem, or they concentrate on subcortical structures or the cerebellum, or alternately represent tractographic connectivity. The full-brain atlases include Harvard’s Surgical Planning Laboratory (SPL) Atlas, atlases available with Oxford’s FMRIB Software Library (FSL), which are listed on FSL’s wiki (FSL), and the Freesurfer software package [11, 12]. To our knowledge, none of these digital atlases is dedicated to the brainstem, which relates to the paucity of printed atlases that center on the brainstem, with the exception of the Duvernoy [20]. The only competing option is the Mai online atlas [19], but its brainstem is low-resolution and not as descriptive as the Duvernoy, while the printed version of the Mai atlas [18] does not include the brainstem.
The main clinical motivation for this minimally supervised segmentation tool of the brainstem is two-fold, to enable the production of patient-specific models of the cranial and spinal nerves in the torso, such as depicted in Fig. 1, and to produce models of the neuroanatomy of the skull base, including the intracranial portion of the cranial nerves depicted in Fig. 2. These models will fulfill an unmet requirement of descriptive neuroanatomy for surgery planning and simulation for cervical spine procedures as well as skull base procedures such as radiotherapy of brainstem gliomas and resection of pituitary adenomas and acoustic neuromas.
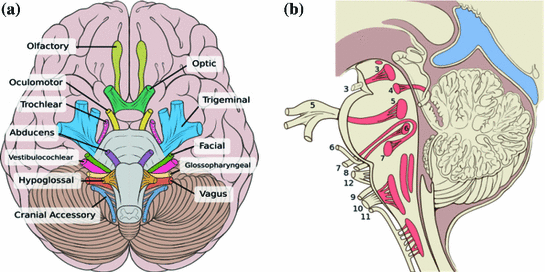

Fig. 2
Relevance to intracranial neuroanatomy: cranial nerves, with nerves III (oculomotor) to XII (hypoglossal) having nuclei within, and attachment points on, the brainstem; a inferior view; b sagittal view with cranial nerve nuclei and tracts inside the brainstem shaded red (reproduced from [9])
In particular, we plan on using probabilistic knowledge of the position of the tracts, or attachment points, of the cranial nerve in the brainstem to enable model-based identification of cranial nerves, in a manner analogous to the path of a clothesline being constrained by the position of the two poles at each end of it. Each attachment point on the brainstem equates with the inner pole of the clothesline, while the position of the corresponding foramen will provide the other, outer pole. Shape statistics of these nerves will provide information on the tortuosity of the clothesline.
The clinical importance of detailed, patient-specific modeling of cranial and cervical spinal nerves is multi-faceted. First, several complications have arisen in the past due to iatrogenic damage in the skull base and spine by surgery and radiotherapy, which could have been prevented by more descriptive surgery planning as well as surgery simulation that would have penalized gestures deleterious to these structures. Second, topological variability in the form of anastomoses, or unusual connections, can occur between cervical spinal nerves and cranial nerves, and patient-specific descriptive modeling of the anatomy for planning and simulation must cope with this variability [27].
Iatrogenic complications in neuro- and head-and-neck surgery, alluded to in the previous paragraph, still have an impact on patient outcome in a large number of cases. We argue strongly that improved surgery planning for experts and surgery simulation for residents would have probably improved patient outcome, at least in terms of morbidity and mortality statistics. Iatrogenic complications in neuro- and head-and-neck surgery include the following cases.
The spinal accessory nerve (SAN), which is depicted in Fig. 1b, has been described as susceptible to injury in head-and-neck surgery by several authors [5, 31]. Estimates of SAN injury incidence in diagnostic lymph node biopsies of the posterior triangle of the neck are 3–8 %.
In brain surgery procedures, a number of complications have been documented in relation to iatrogenic damage or compression of cranial nerves.
The susceptibility to injury of the optical and oculomotor nerves in pituitary surgery was reported in [7]. Amongst 939 neuro-surgeons surveyed, 179 reported post-operative visual loss in one or more patients.
The vulnerability of cranial nerves was noted in the case of an acoustic neuroma patient [23]. Her bone-embedded tumor was resected with an ultrasonic surgical aspirator at 80 % power. The patient experienced right-sided palsies of the 5th, 6th, 7th, and 12th cranial nerves.
As described in [4], oropharyngeal dysphagia, or swallowing disorder, can arise due to neurological dysfunction related to surgical complications of posterior fossa and skull base surgery.
As suggested above, in order to improve patient outcome in neuro- and head-and-neck surgery, surgical planning and simulation must model cranial and cervical nerves explicitly and on a patient-specific basis, which must exploit both modeling that integrates shape priors, i.e. a probabilistic digital atlas, as well as tractographic imaging of the nerves. MRI-based diffusion tensor imaging has been developed for cranial, spinal and peripheral nerves [16, 24, 25], although tractographic reconstruction of these images is still in its infancy, in contrast with tractography of the brain itself [2].
Moreover, to enable minimally supervised, highly descriptive, patient-specific identification of cranial and cervical nerves, we believe that a digital atlas for their most prevalent topology must first be developed, as a foundation for modeling variations such as those due to anastemoses [27]. One of the objectives of this brainstem atlas is to serve as cornerstone for the development of a cranial and cervical nerve atlas, which in turn will be used to stabilize the tractographic reconstruction of these nerves from diffusion imaging data, irrespective of their patient-specific topology.
Finally, treatment of brainstem tumors is still viewed as challenging, where surgical treatment is usually not an option, and chemotherapy is of limited utility. However, radiotherapy in the form of Gamma Knife radiosurgery (GKRS) has emerged as a promising treatment [22]. We suggest that atlas-based functional parcellation of brainstem could have the same potentiating effect on brainstem radiosurgery as the whole-brain functional atlas, further potentiated by fMRI, has had on the sparing of functionally important, eloquent areas in neurosurgery of the brain these past few years. As a result, it is not only the elaboration of cranial nerves that is clinically important in this project, but also the parcellation of the brainstem itself into functional regions.
1.3 Technical Motivation
This paper describes on-going work on the transposition to 3D digital format of a unique printed atlas of the brainstem [20]. This atlas, unlike the Mai atlas of the whole brain for example, does not offer intensity or color cues for regions that we can exploit to facilitate the segmentation. It only features closed contours with numbers imbedded in these regions, which are mostly without color. Moreover, the images also feature open contours that can penetrate some of these regions; a number of these contours coincide with embedded cranial nerves within the brainstem, while others represent symbols of medullary pyramids. At a minimum, these open contours must be purged from the closed contours to enable the labeling of the latter; however in many cases, we must model the embedded cranial nerves to make explicit the corresponding nucleus as well as the attachment point outside the brainstem.
Patient-specific anatomical modeling for neurosurgery planning and simulation entails medical image segmentation, which ideally is minimally supervised and describes the relationship between intensities in medical images, typically MRI or CT data, to anatomically or functionally relevant tissues or structures. Minimally supervised medical image segmentation generally falls under three categories: voxel, boundary and atlas-based, with some overlap being possible. In general, an atlas-based approach enables a functional or anatomical representation of tissues that is far more descriptive than is feasible with the other two methodologies.
Voxel-based approaches involve algorithms based on local properties at each point or voxel. Voxel-based methods tend to be limited to identifying a small number of tissues that they can differentiate, and to be vulnerable to bleeding effects in low contrast, given their paucity of model-based safeguards. The boundary-based approach exploits an active model featuring a trade-off between an internal representation of the tissue boundary, which typically favors a smooth result as well as probabilistic shape priors, and external influences based on intensity gradients or region homogeneity.
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree