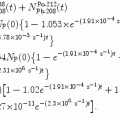(1)
Faculty of Medicine, Department, of Oncology and Medical Physics Unit, McGill University, Montreal, Québec, Canada
Abstract
Chapter 11 consists of 22 problems covering 13 sections that deal with most important modes of radioactive decay. Radioactive nuclides, either naturally occurring or artificially produced by nuclear reactions, are unstable and strive to reach more stable nuclear configurations through various processes of spontaneous radioactive decay that involve transformation to a more stable nuclide and emission of energetic particles. The early investigators of radioactivity explained the macroscopic kinetics of radioactive decay soon after Becquerel’s discovery of natural radioactivity in 1896 through the work of Marie Skłodowska-Curie, Pierre Curie, Ernest Rutherford and Frederick Soddy. However, it took several decades before the various radioactive decay modes were fully understood on a microscopic scale.
Currently, the most important modes of radioactive decay are: alpha, beta minus, beta plus, electron capture, gamma and internal conversion. In addition to these standard modes, questions in this chapter also cover proton and neutron decay as well as spontaneous fission as interesting examples of spontaneous radioactive decay despite their limited relevance to medical physics.
Section 11.1 of this chapter contains one problem covering a general introduction to radioactive decay processes, Sect. 11.2 covers theoretical and practical aspects of alpha decay, Sect. 11.3 deals with general aspects of beta decay, while Sects. 11.4 and 11.5 cover beta minus and beta plus decay, respectively.
Electron capture decay is addressed in Sect. 11.6. Sections 11.7 and 11.8, respectively, cover gamma decay and its competing process, internal conversion. Section 11.9 addresses spontaneous fission and Sects. 11.10 and 11.11 deal with proton emission decay and neutron emission decay, respectively. Next comes Sect. 11.12 that contains several problems concentrating on the Chart of Nuclides (also called Segrè chart) and the chapter concludes with problems in Sect. 11.13 that deal with a summary of issues related to radioactive decay modes.
Chapter 11 consists of 22 problems covering 13 sections that deal with most important modes of radioactive decay. Radioactive nuclides, either naturally occurring or artificially produced by nuclear reactions, are unstable and strive to reach more stable nuclear configurations through various processes of spontaneous radioactive decay that involve transformation to a more stable nuclide and emission of energetic particles. The early investigators of radioactivity explained the macroscopic kinetics of radioactive decay soon after Becquerel’s discovery of natural radioactivity in 1896 through the work of Marie Skłodowska-Curie, Pierre Curie, Ernest Rutherford and Frederick Soddy. However, it took several decades before the various radioactive decay modes were fully understood on a microscopic scale.
Currently, the most important modes of radioactive decay are: alpha, beta minus, beta plus, electron capture, gamma and internal conversion. In addition to these standard modes, questions in this chapter also cover proton and neutron decay as well as spontaneous fission as interesting examples of spontaneous radioactive decay despite their limited relevance to medical physics.
Section 11.1 of this chapter contains one problem covering a general introduction to radioactive decay processes, Sect. 11.2 covers theoretical and practical aspects of alpha decay, Sect. 11.3 deals with general aspects of beta decay, while Sects. 11.4 and 11.5 cover beta minus and beta plus decay, respectively.
Electron capture decay is addressed in Sect. 11.6. Sections 11.7 and 11.8, respectively, cover gamma decay and its competing process, internal conversion. Section 11.9 addresses spontaneous fission and Sects. 11.10 and 11.11 deal with proton emission decay and neutron emission decay, respectively. Next comes Sect. 11.12 that contains several problems concentrating on the Chart of Nuclides (also called Segrè chart) and the chapter concludes with problems in Sect. 11.13 that deal with a summary of issues related to radioactive decay modes.
11.1 Introduction to Radioactive Decay Processes
11.1.Q1 (224)
Radioactive nuclides, either naturally occurring or produced artificially by nuclear reactions, are unstable and strive to reach more stable nuclear configurations through various processes of spontaneous radioactive decay that involve nuclear transformation to a more stable nuclide and emission of energetic particles.
(a)
A closer look at radioactive decay processes reveals that they are divided into six main categories. Provide a list of the six main categories of nuclear decay.
(b)
Two of the six nuclear decay categories are divided into subcategories. Identify these two categories and list their subcategories.
(c)
On a microscopic scale there are nine major modes of radioactive decay. List the nine modes of nuclear decay.
(d)
For each of the major nine modes of nuclear decay identify the particle that is released in the nuclear decay mode.
(e)
List the most important physical quantities that must be conserved in nuclear decay.
(f)
For radioactive nuclear decay define the disintegration or decay energy that is often also referred to as Q value of radioactive decay.
(g)
Explain the meaning of terms: “neutron-rich” and “proton rich”.
SOLUTION:
(a) The six main categories of radioactive nuclear decay are:
(b) The two categories of radioactive nuclear decay that are divided into subcategories are:
(c) The nine major modes of radioactive nuclear decay are:
(d) In each mode of radioactive nuclear decay the parent P nucleus transforms into a daughter D nucleus that differs from the parent nucleus in one or more of the following parameters: atomic number Z, neutron number N, and atomic mass number A. In addition, in each mode of nuclear decay one or more particles are released, as listed in Table 11.1.
(1)
Alpha (α) decay
(2)
Beta (β) decay
(3)
Gamma (γ) decay
(4)
Spontaneous fission (SF)
(5)
Proton emission (PE) decay
(6)
Neutron emission (NE) decay
(1)
Beta (β) decay that is subdivided into: beta minus (β −) decay, beta plus (β +) decay, and electron capture (EC) decay.
(2)
Gamma (γ) decay that is subdivided into gamma emission (GE) decay and internal conversion (IC) decay.
(1)
α decay
(2)
β − decay
(3)
β + decay
(4)
Electron capture (EC)
(5)
γ emission decay
(6)
Internal conversion (IC)
(7)
Spontaneous fission (SF)
(8)
Proton emission decay
(9)
Neutron emission decay
Table 11.1
Modes of radioactive nuclear decay and particles released in nuclear decays
Mode of radioactive nuclear decay | Particles released in radioactive nuclear decay | |
|---|---|---|
(1) | α | α particle (helium nucleus) |
(2) | β − | Electron e− and electronic antineutrino 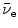 |
(3) | β + | Positron e+ and electronic neutrino ν e |
(4) | EC (electron capture) | Electronic neutrino ν e |
(5) | Gamma emission | γ ray photon |
(6) | IC (internal conversion) | Atomic orbital electron eorb |
(7) | SF (spontaneous fission) | Neutron and fission product nuclei |
(8) | Proton emission | Proton |
(9) | Neutron emission | Neutron |
(e) Most important physical quantities that must be conserved in radioactive nuclear decay are:
(f) Total energy of particles released by the nuclear transformation process is equal to the net decrease in the rest energy of the neutral atom, from parent P to daughter D. The disintegration (decay) energy, often referred to as Q value for the radioactive decay, is defined as follows
![$$ Q = \bigl\{ M(\mathrm{P}) - \bigl[M(\mathrm{D}) + m\bigr] \bigr \}c^{2}, $$](/wp-content/uploads/2016/04/A212719_1_En_11_Chapter_Equ1.gif)
where M(P), M(D), and m are the nuclear rest masses (in unified atomic mass units u) of the parent, daughter, and emitted particles, respectively. The energy equivalent of u is 931.5 MeV.
(1)
Total energy
(2)
Momentum
(3)
Total charge
(4)
Atomic number
(5)
Atomic mass number (number of nucleons)
![$$ Q = \bigl\{ M(\mathrm{P}) - \bigl[M(\mathrm{D}) + m\bigr] \bigr \}c^{2}, $$](/wp-content/uploads/2016/04/A212719_1_En_11_Chapter_Equ1.gif)
(11.1)
Often atomic masses rather than nuclear masses are used in calculations of Q values for radioactive decay. In many decay modes the electron masses cancel out, so that it makes no difference if atomic or nuclear masses are used in (11.1). On the other hand, there are situations where electron masses do not cancel out (e.g., β + decay) and there special care must be taken to account for all electrons involved when atomic rest masses are used in (11.1).
For radioactive decay to be energetically possible the Q value must be greater than zero. This means that spontaneous radioactive decay processes release energy and are called exoergic or exothermic. For Q>0, the energy equivalent of the Q value is shared as kinetic energy between the particles emitted in the decay process and the daughter product. Since the daughter has a much larger mass than the other emitted particles, the kinetic energy acquired by the daughter is usually negligibly small.
(g) In light (low atomic number) elements nuclear stability is achieved when the number of neutrons N and the number of protons Z is approximately equal (N≈Z). As the atomic number increases, the N/Z ratio for stable nuclei increases from 1 at low Z elements to about 1.5 for heavy stable elements.
(1)
If a nucleus has a N/Z ratio that is too low for nuclear stability, it has an excess of protons and is called proton-rich. It decays through conversion of a proton into a neutron and emits a positron and a neutrino (β + decay). Alternatively, the nucleus may capture an orbital electron, transform a proton into a neutron and emit a neutrino (electron capture). A direct emission of a proton is also possible, but less likely, unless the nuclear imbalance is very high.
(2)
If a nucleus has a N/Z ratio too high for nuclear stability, it has an excess of neutrons and is called neutron-rich. It decays through conversion of a neutron into a proton and emits an electron and anti-neutrino. This process is referred to as β − decay. If the N/Z ratio is extremely high, a direct emission of a neutron is possible.
11.2 Alpha Decay
11.2.Q1 (225)
Alpha (α) decay was the first mode of radioactive decay detected and investigated after Henri Becquerel discovered natural radioactivity in 1896. It played an important role in early modern physics experiments that lead to the currently accepted Rutherford-Bohr atomic model and is characterized by a nuclear transformation in which an unstable parent nucleus P attains a more stable nuclear configuration in daughter D through ejection of an α particle.
(a)
Briefly discuss the history of α decay and explain its historical significance for physics in particular and science in general.
(b)
List three methods that are used to calculate decay energy Q α (P) that is often also referred to as Q value of α decay
(c)
List and briefly describe the important features of α decay.
(d)
Q value of α decay is of similar magnitude but not equal to kinetic energy (E K) α of the α particle ejected in α decay. Explain the difference between the two energies.
(e)
(E K) α is often expressed as (E K) α ≈Q α (P)[1−4/A P]. Show and explain the derivation of this approximation.
SOLUTION:
(a) Alpha particles produced in natural α decay were used in one of the most important experiments in history of physics and science in general when Hans Geiger and Ernest Marsden carried out their momentous 1909 study of α particle scattering on a gold foil. Based on their experimental results that clearly contradicted the then-prevailing Thomson atomic model, Ernest Rutherford proposed a completely new atomic model with two main features:
Despite importance of α particles in early nuclear physics experiments, attempts to explain alpha decay theoretically were unsuccessful until 1928 when George Gamow unraveled its exact nature by introducing into physics the quantum-mechanical concept of tunneling of α particles through a potential barrier.
(1)
Mass and positive charge of the atom are concentrated in the atomic nucleus the size of which is of the order of 10−15 m=1 fm, i.e., 5 orders of magnitude smaller than the size of the atom.
(2)
Negatively charged electrons revolve about the nucleus in a cloud, the radius of which is of the order 10−10=1 Å.
(b) Similarly to the calculation of the Q value of a nuclear reaction in which a projectile strikes a nuclear target to produce two reaction products, in nuclear α decay of parent P nucleus that results in daughter D nucleus and emission of an α particle, the α decay Q value or Q α can be determined with three methods:
(c) The prominent features of α decay are summarized as follows:
(d) In α decay the principles of energy and momentum conservation must be upheld and as a result α decay energy Q α is shared between daughter atom and α particle. For a stationary parent nucleus the momentum before decay is zero, implying that the α particle and daughter atom together must have zero momentum after decay. This can be achieved only if the two decay products (α particle and daughter atom) acquire momenta opposite in direction and equal in magnitude
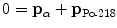
or
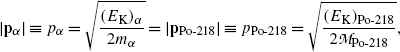
where p α and p D are vector momenta of the α particle and daughter atom, respectively, and |p α |≡p α and |p D|=p D are magnitudes of the momentum vectors of the α particle and daughter atom, respectively.
(1)
Atomic rest energy method in which one subtracts the sum of atomic rest energies of decay products after the α decay (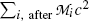 ) from atomic rest energy of the parent atom
) from atomic rest energy of the parent atom 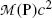
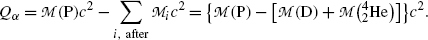
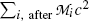 ) from atomic rest energy of the parent atom
) from atomic rest energy of the parent atom 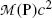
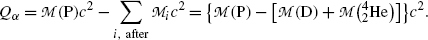
(11.2)
(2)
Nuclear rest energy method in which one subtracts the sum of nuclear rest energies of decay products after the decay (∑ i, after M i c 2) from the rest energy of the parent nucleus M(P)c 2
![$$ Q_{\alpha} = M(\mathrm{P})c^{2} - \sum _{i,\ \mathrm{after}} M_{i} c^{2} = \bigl\{ M(\mathrm{P}) - \bigl[M(\mathrm{D}) + m_{\alpha} \bigr]\bigr\} c^{2}. $$](/wp-content/uploads/2016/04/A212719_1_En_11_Chapter_Equ3.gif)
![$$ Q_{\alpha} = M(\mathrm{P})c^{2} - \sum _{i,\ \mathrm{after}} M_{i} c^{2} = \bigl\{ M(\mathrm{P}) - \bigl[M(\mathrm{D}) + m_{\alpha} \bigr]\bigr\} c^{2}. $$](/wp-content/uploads/2016/04/A212719_1_En_11_Chapter_Equ3.gif)
(11.3)
(3)
Nuclear binding energy method in which the binding energy E B(P) of the parent nucleus before decay is subtracted from the sum of binding energies of decay products after the decay (∑ i,after E B(P))
![$$ Q_{\alpha} = \sum_{i,\mathrm{after}} E_{\mathrm{B}}(i) - E_{\mathrm{B}}(\mathrm{P}) = \bigl[E_{\mathrm{B}}(\mathrm{D}) + E_{\mathrm{B}} \bigl({}_{2}^{4}\mathrm{He}\bigr)\bigr] - E_{\mathrm{B}}( \mathrm{P}). $$](/wp-content/uploads/2016/04/A212719_1_En_11_Chapter_Equ4.gif)
![$$ Q_{\alpha} = \sum_{i,\mathrm{after}} E_{\mathrm{B}}(i) - E_{\mathrm{B}}(\mathrm{P}) = \bigl[E_{\mathrm{B}}(\mathrm{D}) + E_{\mathrm{B}} \bigl({}_{2}^{4}\mathrm{He}\bigr)\bigr] - E_{\mathrm{B}}( \mathrm{P}). $$](/wp-content/uploads/2016/04/A212719_1_En_11_Chapter_Equ4.gif)
(11.4)
(1)
In α decay, the number of protons Z and the number of neutrons N is conserved by producing a 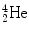 nucleus (α particle) and lowering the parent’s atomic mass number A P by 4 and parent’s atomic number Z P by 2 to get a daughter with A D=A P−4 and Z D=Z P−2, i.e.,
nucleus (α particle) and lowering the parent’s atomic mass number A P by 4 and parent’s atomic number Z P by 2 to get a daughter with A D=A P−4 and Z D=Z P−2, i.e.,
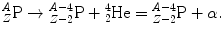
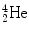 nucleus (α particle) and lowering the parent’s atomic mass number A P by 4 and parent’s atomic number Z P by 2 to get a daughter with A D=A P−4 and Z D=Z P−2, i.e.,
nucleus (α particle) and lowering the parent’s atomic mass number A P by 4 and parent’s atomic number Z P by 2 to get a daughter with A D=A P−4 and Z D=Z P−2, i.e.,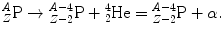
(11.5)
(2)
The energetic α particle emitted in α decay slows down in moving through the absorber medium and eventually captures two electrons from its surroundings to become a neutral 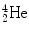 atom.
atom.
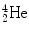 atom.
atom.(3)
Typical kinetic energies of α particles released by naturally occurring radionuclides are between 4 MeV and 9 MeV, corresponding to a range in air of about 1 cm to 10 cm, respectively, and in tissue of about 10−3 cm and 10−2 cm, respectively.
(4)
α decay occurs commonly in nuclei with Z>82 because in this range of atomic number Z decay energies Q α determined in (b) are positive and of the order of ∼4 MeV to ∼9 MeV.
(5)
Total decay energy Q α must be positive for α decay to occur and the Q α >0 results mainly from the high total binding energy of the 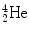 nucleus (29.3 MeV) that is significantly higher than for nuclei of
nucleus (29.3 MeV) that is significantly higher than for nuclei of 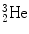 ,
, 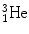 , and
, and 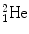 for which spontaneous ejection from parent nuclei energetically is not feasible.
for which spontaneous ejection from parent nuclei energetically is not feasible.
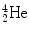 nucleus (29.3 MeV) that is significantly higher than for nuclei of
nucleus (29.3 MeV) that is significantly higher than for nuclei of 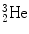 ,
, 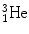 , and
, and 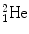 for which spontaneous ejection from parent nuclei energetically is not feasible.
for which spontaneous ejection from parent nuclei energetically is not feasible.(6)
Ejection of a heavy nucleus from the parent nucleus is energetically possible (large Q value); however, the effect of tunneling through the potential barrier is then also much more difficult for the heavy nucleus in comparison with tunneling for the α particle.
(7)
Emission of heavy particles from parent nuclei with Z>92 is possible and represents a mode of radioactive decay competing with α decay and referred to as spontaneous fission.
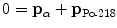
(11.6)
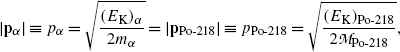
(11.7)
Considering total energy conservation we recognize that kinetic energies of decay products in α decay are relatively small allowing us to use classical mechanics for expression of energy conservation to get the following expression for the decay energy Q α (P)
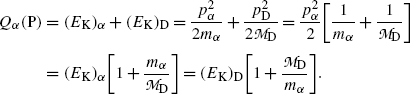
From (11.8) we extract the following expressions for kinetic energies (E K) α and (E K)D of α decay products
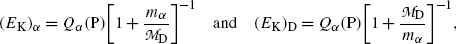
where Q α (P) is the α decay energy (Q value) determined through one of the three methods introduced in (b). Noting that in α decay 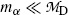 , (11.9) suggests that the α particle and daughter D atom will share the decay energy Q α (P) in the inverse proportion of their masses, resulting in a large portion of the available energy Q α going to the α particle and only a small percentage of Q α transferred to the daughter atom.
, (11.9) suggests that the α particle and daughter D atom will share the decay energy Q α (P) in the inverse proportion of their masses, resulting in a large portion of the available energy Q α going to the α particle and only a small percentage of Q α transferred to the daughter atom.
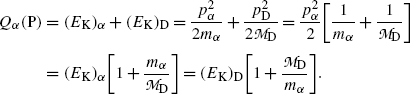
(11.8)
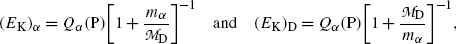
(11.9)
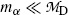 , (11.9) suggests that the α particle and daughter D atom will share the decay energy Q α (P) in the inverse proportion of their masses, resulting in a large portion of the available energy Q α going to the α particle and only a small percentage of Q α transferred to the daughter atom.
, (11.9) suggests that the α particle and daughter D atom will share the decay energy Q α (P) in the inverse proportion of their masses, resulting in a large portion of the available energy Q α going to the α particle and only a small percentage of Q α transferred to the daughter atom.(e) Equations (11.9) for kinetic energies (E K) α and (E K)D of the α particle and daughter atom, respectively, can be approximated as follows provided that 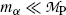
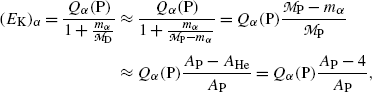
where A P is the atomic mass number of the parent nucleus and A He=4 is the atomic mass number of the helium nucleus.
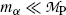
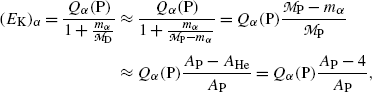
(11.10)
Similarly, we get the following approximation for the recoil kinetic energy (E K)D of the daughter atom D
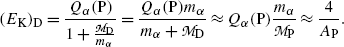
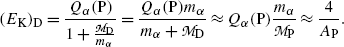
(11.11)
11.2.Q2 (226)
Radon is an inert noble gas that mixes with air and has 36 known isotopes, all radioactive. It occurs naturally as the decay product of uranium or thorium, and its most common isotope is radon-222 which is a daughter product of radium-226 decay. Radon daughters are solids that attach themselves to dust particles in air and pose a radiation risk to humans when inhaled causing bronchial and lung tissue damage possibly leading to lung cancer.
(a)
Determine decay energy Q α for the α decay of radon-222 into polonium-218. Use and compare three methods for Q α calculation: (1) Atomic rest energy method, (2) Nuclear rest energy method, and (3) Nuclear binding energy method. All required atomic and nuclear data are provided in Appendix A.
(b)
Determine kinetic energy (E K) α of the α particle emitted in the Rn-222 α decay.
(c)
Determine recoil kinetic energy (E K)Po-218 of polonium-218 daughter in Rn-222 α decay.
(d)
Find a decay scheme of radon-222 in the literature and verify whether or not your result of (b) agrees with the decay scheme you found in the literature.
SOLUTION:
(a) Decay energy or Q value of the radioactive nuclear α decay can be calculated with three methods and all three are expected to give the same result (see T11.1). The three methods are: (1) Atomic rest energy method (T11.3), (2) Nuclear rest energy method (T11.3), and (3) Nuclear binding energy method (T11.4).
(b) We now use the principles of (1) total energy conservation and (2) momentum conservation to determine kinetic energy (E K) α of the α particle ejected in the α decay of radon-222 and recoil energy (E K)Po-218 of the polonium-218 daughter product. The two conservation principles are for α decay expressed as follows:
where
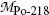
Using (11.15) we can now express the conservation of energy as
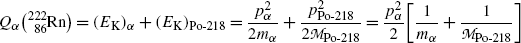
from where it follows that
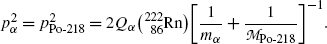
Inserting (11.19) into (11.18) we now get the following expressions for (E K) α and (E K)Po-218
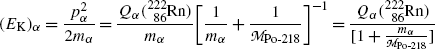
![$$\begin{aligned} =& \frac{5.59\ \mathrm{MeV}}{ [ 1 + \frac{3727.3791}{203074.0564} ]} = \frac{5.59\ \mathrm{MeV}}{1.0184} = 5.49\ \mathrm{MeV} \end{aligned}$$](/wp-content/uploads/2016/04/A212719_1_En_11_Chapter_Equ21.gif)
and
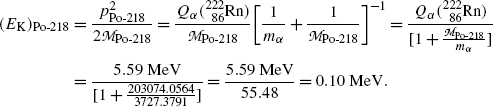
Same results can be obtained with the approximations presented in (T11.7) as
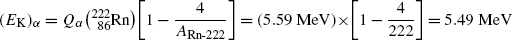
and
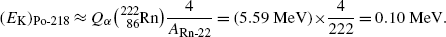
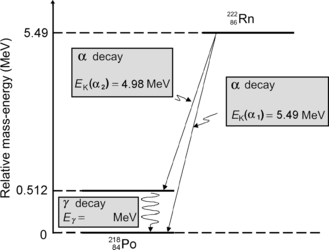
(d) In Fig. 11.1 we show the energy level diagram we found in the literature for α decay of radon-222 into polonium-218. Our calculated kinetic energy (E K) α =5.49 MeV of the α particle that radon-222 emits in its decay into polonium-218 agrees well with the published data.
(1)
Atomic rest energy method:
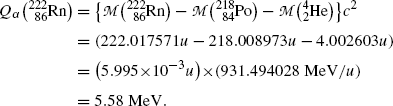
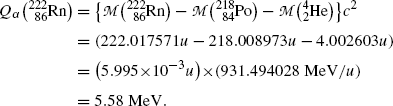
(11.12)
(2)
Nuclear rest energy method:
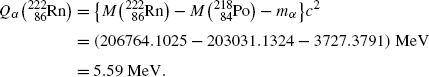
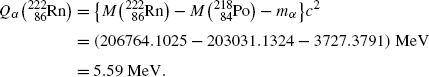
(11.13)
(3)
Nuclear binding energy method:
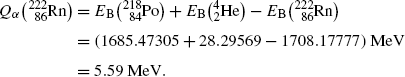
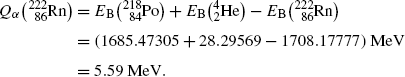
(11.14)
(1)
For total energy conservation we recognize that kinetic energies in α decay are relatively small allowing us to use classical mechanics for expression of energy conservation
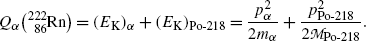
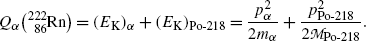
(11.15)
(2)
For momentum conservation we note that momentum before α decay is zero causing the two momenta p α and p Po-218 after the α decay to be opposite in direction and equal in magnitude
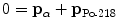
or
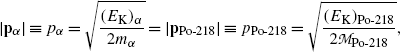
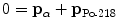
(11.16)
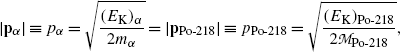
(11.17)
p α
is the magnitude of α particle momentum.
p Po-218
is the magnitude of the polonium-218 atomic recoil momentum.
m α
is the rest mass of the α particle.
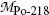
is the rest mass of the polonium-218 atom
(218.008973 u)×(931.494028 MeV/u)=203074.0564 MeV/c 2.
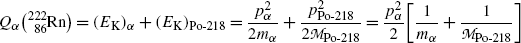
(11.18)
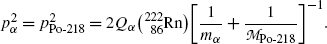
(11.19)
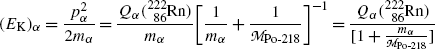
(11.20)
![$$\begin{aligned} =& \frac{5.59\ \mathrm{MeV}}{ [ 1 + \frac{3727.3791}{203074.0564} ]} = \frac{5.59\ \mathrm{MeV}}{1.0184} = 5.49\ \mathrm{MeV} \end{aligned}$$](/wp-content/uploads/2016/04/A212719_1_En_11_Chapter_Equ21.gif)
(11.21)
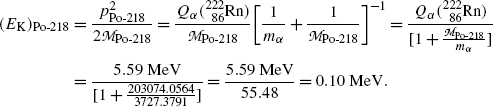
(11.22)
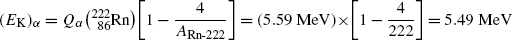
(11.23)
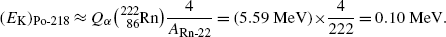
(11.24)

Fig. 11.1
Energy level diagram for α decay of radon-222 into polonium-218. The relative mass-energy levels for the ground states of the two radionuclides are calculated for the respective atomic masses of the two radionuclides given in Appendix A
11.3 Beta Decay
11.3.Q1 (227)
The term beta decay encompasses 3 modes of radioactive decay in which the atomic number Z between the parent and the daughter nuclide changes by one unit (±1), while the atomic mass number A remains constant. Thus, the number of nucleons and the total charge are both conserved in the beta decay processes and one can say that the daughter D is an isobar of the parent P, since the two contain the same number of nucleons.
(a)
List and briefly discuss the three radioactive decay processes that belong to the beta decay category.
(b)
Often a β decay process of the parent is accompanied by emission of characteristic x rays or Auger electrons emitted by the daughter nucleus. Describe the mechanisms of these events.
(c)
In α decay the emitted α particles are mono-energetic for a given α decay process. In β decay, however, β particles (electrons in β − decay or positrons in β + decay) are emitted with a spectral distribution. Explain why this is so and sketch a typical β emission spectrum for electrons and positrons.
(d)
In β − and β + decay the daughter D recoils with kinetic energy (E K)D ranging from 0 to a maximum value. Explain the conditions under which (1) (E K)D=0 and (2) (E K)D=max.
(e)
Q value of β decay (also referred to as decay energy Q β ) can be expressed as the sum of kinetic energies of β decay products after β decay. Derive an expression for Q β the as a function of the maximum energy (E β )max of the beta particle after β decay.
(f)
From the result for Q β in (e) express (E β )max as a function of Q β and show that in the first approximation (E β )max≈Q β (1−η β ), where η β is a very small correction factor. Determine the correction factor η β .
SOLUTION:
(a) Three processes fall into the category of β decay:
(b) In many cases, β decay of a parent nucleus does not lead directly to the ground state of the daughter nucleus; rather it leads to an unstable or even metastable excited state of the daughter. The excited state de-excites through emission of gamma rays or through emission of internal conversion electrons. Of course, the orbital shell vacancies produced by the electron capture or internal conversion process will be followed by emission of discrete characteristic photons or Auger electrons, as is the case with all atomic shell vacancies no matter how they are produced.
(1)
Beta minus (β −) decay with the following characteristics: Z→Z+1; A=const.
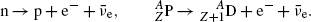
A neutron-rich radioactive nucleus transforms a neutron into proton and ejects an electron and an antineutrino. Free (extra-nuclear) neutrons actually decay into protons through the β − decay process with a lifetime τ of 11.24 min. This decay is possible since the neutron rest mass exceeds that of the proton.
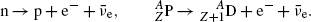
(11.25)
(2)
Beta plus (β +) decay with the following characteristics: Z→Z−1; A=const.
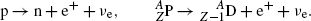
A proton-rich radioactive nucleus transforms a proton into neutron and ejects a positron and a neutrino. Free (extra-nuclear) protons cannot decay into neutrons through a β + decay process because the rest mass of the proton is smaller than that of the neutron.
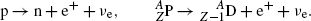
(11.26)
(3)
Electron capture with the following characteristics: Z→Z−1; A=const.
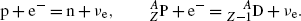
A proton-rich radioactive nucleus captures an inner shell orbital electron (usually K shell), transforms a proton into a neutron, and ejects a neutrino.
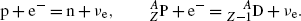
(11.27)
Beta decay can only take place when the binding energy of the daughter nucleus E B(D) exceeds the binding energy of the parent nucleus E B(P).
(c) For a given β decay, similarly to the situation in α decay, the β-decay energy is uniquely defined by the difference in mass-energy between the parent and daughter nuclei. However, in contrast to the α decay where the energy of the emitted α particles is also uniquely defined, the β particles emitted in β decay are not mono-energetic, rather they exhibit a continuous spectral kinetic energy distribution with only the maximum kinetic energy (E e)max corresponding to the β decay energy.
This apparent contravention of the energy conservation law was puzzling physicists for many years until in 1930 Wolfgang Pauli postulated the existence of the neutrino to explain the continuous spectrum of electrons emitted in β decay. In 1934 Enrico Fermi expanded on Pauli’s neutrino idea and developed a theory of β − and β + decay. The theory includes the neutrino or the antineutrino as the third particle sharing the available decay energy and momentum with the β particle and the recoil nucleus. With the emission of a third particle, the neutrino or antineutrino, the momentum and energy can be conserved in β decay.
Typical shapes of β − and β + spectra are shown in Fig. 11.2. In general, the spectra exhibit low values at small kinetic energies, reach a maximum at a certain kinetic energy, and then decrease with kinetic energy until they reach zero at a maximum energy [(E K) β ]max that corresponds to the β decay energy Q β , if we neglect the small recoil energy acquired by the daughter nucleus.
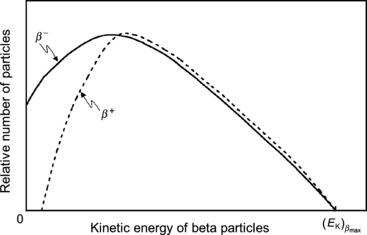

Fig. 11.2
Typical β particle energy spectra for β − and β + decay normalized to the maximum energy of the β particles
The shapes of β − and β + spectra differ at low kinetic energies owing to the charge of the β particles: electrons in β − decay are attracted to the nucleus; positrons in β + decay are repelled by the nucleus. The charge effects cause an energy shift to lower energies for electrons and to higher energies for positrons, as is clearly shown in Fig. 11.2.
For use in internal dosimetry calculations of β sources the effective energy [(E K) β ]eff of β decay spectra is usually estimated as
![$$ \bigl[(E_{\mathrm{K}})_{\beta} \bigr]_{\mathrm{eff}} = \frac{1}{3} \bigl[(E_{\mathrm{K}})_{\beta} \bigr]_{\max }. $$](/wp-content/uploads/2016/04/A212719_1_En_11_Chapter_Equ28.gif)
(d) Because of the presence of the third decay product (the elusive neutrino or antineutrino) in β decay that shares the available decay energy Q β , the recoil energy (E K)D can take on values between zero and a maximum value.
![$$ \bigl[(E_{\mathrm{K}})_{\beta} \bigr]_{\mathrm{eff}} = \frac{1}{3} \bigl[(E_{\mathrm{K}})_{\beta} \bigr]_{\max }. $$](/wp-content/uploads/2016/04/A212719_1_En_11_Chapter_Equ28.gif)
(11.28)
(1) Recoil kinetic energy of the daughter decay product is zero, i.e., (E K)D=0, when the electron and antineutrino in β − decay or positron and neutrino in β + decay are emitted with the same momentum but in opposite directions.
(2) Maximum recoil kinetic energy (E K)D=[(E K)D]max=max of the daughter, on the other hand, occurs when either one of the two light decay particles (electron or antineutrino in β − decay; positron or neutrino in β + decay) is emitted with the maximum available kinetic energy [(E K) β ]max.
(e) Q value of β decay or β-decay energy Q β is expressed as the sum of kinetic energies of decay products after the β decay. For simplicity we use [(E K)D]max and (E K)max in the sum to get
![$$ Q_{\beta} = \bigl[(E_{\mathrm{K}})_{\mathrm{D}}\bigr]_{\max } + \bigl[(E_{\mathrm{K}})_{\beta} \bigr]_{\max } $$](/wp-content/uploads/2016/04/A212719_1_En_11_Chapter_Equ29.gif)
and then express [(E K)D]max in terms of [(E K) β ]max.
![$$ Q_{\beta} = \bigl[(E_{\mathrm{K}})_{\mathrm{D}}\bigr]_{\max } + \bigl[(E_{\mathrm{K}})_{\beta} \bigr]_{\max } $$](/wp-content/uploads/2016/04/A212719_1_En_11_Chapter_Equ29.gif)
(11.29)
Maximum recoil kinetic energy of the daughter [(E K)D]max is determined using the principles of energy and momentum conservation and accounting for the relativistic mass changes of the β particle (electron or positron) and using classical mechanics for recoil kinetic energy [(E K)D]max of the daughter.
Since the parent momentum before β decay is zero, the total momentum shared by the daughter D and the β particle e± (under the special condition of neutrino or antineutrino energy equaling zero) must also equal to 0 after the β decay and this means that the two vector momenta p D and 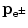 after β decay must be opposite in direction and equal in magnitude. The magnitudes of the two momenta are thus related as follows
after β decay must be opposite in direction and equal in magnitude. The magnitudes of the two momenta are thus related as follows
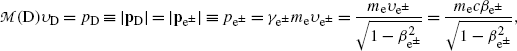
where
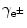
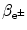
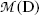
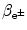
Maximum recoil kinetic energy [(E E)D]max of the daughter is expressed as follows
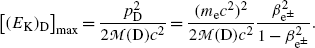
From the standard expression for ![$[(E_{\mathrm{K}})_{\beta} ]_{\max } = (\gamma _{\mathrm{e}^{ \pm}} - 1)m_{\mathrm{e}}c^{2}$](/wp-content/uploads/2016/04/A212719_1_En_11_Chapter_IEq20.gif) we determine the following expression for
we determine the following expression for 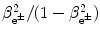
![$$ \frac{\beta _{\mathrm{e}^{ \pm}} ^{2}}{1 - \beta _{\mathrm{e}^{ \pm}} ^{2}} = \frac{2[(E_{\mathrm{K}})_{\beta} ]_{\max }}{m_{\mathrm{e}}c^{2}} + \biggl[ \frac{[(E_{\mathrm{K}})_{\beta} ]_{\max }}{m_{\mathrm{e}}c^{2}} \biggr]^{2}. $$](/wp-content/uploads/2016/04/A212719_1_En_11_Chapter_Equ32.gif)
Inserting (11.32) into (11.31) we obtain the following result for the maximum recoil kinetic energy of the daughter D after β decay
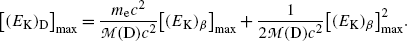
Beta decay energy Q β is now given by the following expression
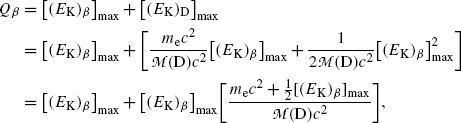
showing clearly that in beta minus decay as well as in beta plus decay by far the larger energy component is the component [(E K) β ]max that is shared between the electron and antineutrino in beta minus decay and by the positron and neutrino in beta plus decay. Recoil energy [(E K)D]max given to the daughter, even at its maximum spelled out in (11.33), is extremely small and generally neglected in comparison with [(E K) β ]max.
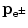 after β decay must be opposite in direction and equal in magnitude. The magnitudes of the two momenta are thus related as follows
after β decay must be opposite in direction and equal in magnitude. The magnitudes of the two momenta are thus related as follows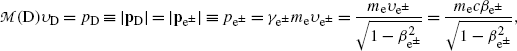
(11.30)
m e
is the rest mass of the β particle (electron or positron): m e=0.511 MeV/c 2.
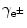
is the Lorentz factor of the beta particle: 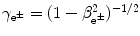 .
.
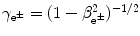 .
.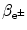
is the velocity 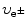 of the β particle normalized to speed of light c.
of the β particle normalized to speed of light c.
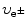 of the β particle normalized to speed of light c.
of the β particle normalized to speed of light c.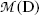
is the atomic rest mass of the daughter β decay product.
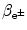
is the velocity of the daughter D after β decay.
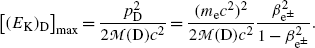
(11.31)
![$[(E_{\mathrm{K}})_{\beta} ]_{\max } = (\gamma _{\mathrm{e}^{ \pm}} - 1)m_{\mathrm{e}}c^{2}$](/wp-content/uploads/2016/04/A212719_1_En_11_Chapter_IEq20.gif) we determine the following expression for
we determine the following expression for 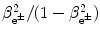
![$$ \frac{\beta _{\mathrm{e}^{ \pm}} ^{2}}{1 - \beta _{\mathrm{e}^{ \pm}} ^{2}} = \frac{2[(E_{\mathrm{K}})_{\beta} ]_{\max }}{m_{\mathrm{e}}c^{2}} + \biggl[ \frac{[(E_{\mathrm{K}})_{\beta} ]_{\max }}{m_{\mathrm{e}}c^{2}} \biggr]^{2}. $$](/wp-content/uploads/2016/04/A212719_1_En_11_Chapter_Equ32.gif)
(11.32)
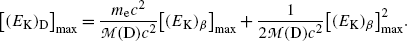
(11.33)
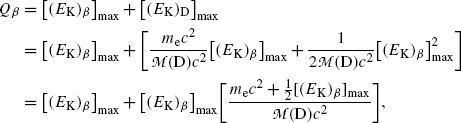
(11.34)
Equation (11.34) can be written in the form of a quadratic equation for [(E K) β ]max as a function of Q β
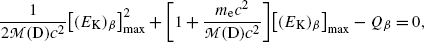
with the following physically-relevant solution [note: [(E K) β ]max>0]
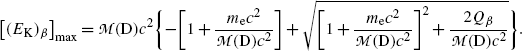
(f) To evaluate (11.36) further we write it in the following form
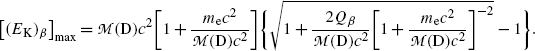
The second term under the square root is obviously much smaller than 1 since it is governed by the ratio 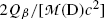 , allowing us to expand the square root into a series and keeping only the first two terms to get
, allowing us to expand the square root into a series and keeping only the first two terms to get
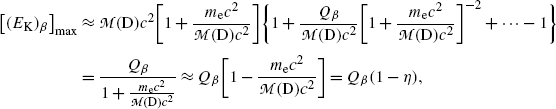
where η β is a small correction factor for β decay given as 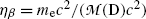 and this ratio multiplied by Q β is actually the maximum recoil kinetic energy [(E K)D]max of the daughter after the β decay
and this ratio multiplied by Q β is actually the maximum recoil kinetic energy [(E K)D]max of the daughter after the β decay
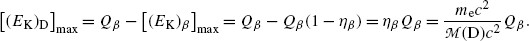
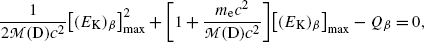
(11.35)
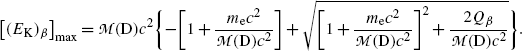
(11.36)
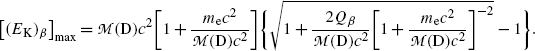
(11.37)
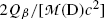 , allowing us to expand the square root into a series and keeping only the first two terms to get
, allowing us to expand the square root into a series and keeping only the first two terms to get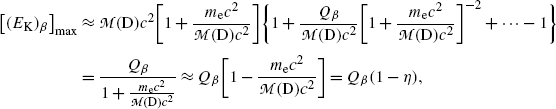
(11.38)
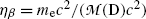 and this ratio multiplied by Q β is actually the maximum recoil kinetic energy [(E K)D]max of the daughter after the β decay
and this ratio multiplied by Q β is actually the maximum recoil kinetic energy [(E K)D]max of the daughter after the β decay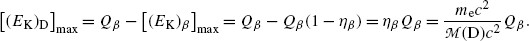
(11.39)
11.4 Beta Minus Decay
11.4.Q1 (228)
Several radionuclides decaying by beta minus (β −) decay are used in medicine for external beam radiotherapy, brachytherapy, and nuclear imaging. Parent P radionuclide decays by β − decay into excited daughter D that instantaneously or through metastable decay, decays into its ground state and emits the excitation energy in the form gamma rays.
(a)
State expressions for β − decay energy 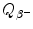 (Q value of β − decay) based on: (1) nuclear rest energy of parent P and daughter D; (2) atomic rest energy of parent P and daughter D.
(Q value of β − decay) based on: (1) nuclear rest energy of parent P and daughter D; (2) atomic rest energy of parent P and daughter D.
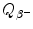 (Q value of β − decay) based on: (1) nuclear rest energy of parent P and daughter D; (2) atomic rest energy of parent P and daughter D.
(Q value of β − decay) based on: (1) nuclear rest energy of parent P and daughter D; (2) atomic rest energy of parent P and daughter D.(b)
Decay energy 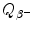 for β − decay can be written as the sum of maximum recoil kinetic energy [(E K)D]max of the daughter and maximum kinetic energy [(E K) β ]max of the β − particle (electron) ejected from the nucleus in β − decay. State the expressions for [(E K)D]max and [(E K) β ]max in terms of
for β − decay can be written as the sum of maximum recoil kinetic energy [(E K)D]max of the daughter and maximum kinetic energy [(E K) β ]max of the β − particle (electron) ejected from the nucleus in β − decay. State the expressions for [(E K)D]max and [(E K) β ]max in terms of 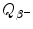 .
.
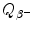 for β − decay can be written as the sum of maximum recoil kinetic energy [(E K)D]max of the daughter and maximum kinetic energy [(E K) β ]max of the β − particle (electron) ejected from the nucleus in β − decay. State the expressions for [(E K)D]max and [(E K) β ]max in terms of
for β − decay can be written as the sum of maximum recoil kinetic energy [(E K)D]max of the daughter and maximum kinetic energy [(E K) β ]max of the β − particle (electron) ejected from the nucleus in β − decay. State the expressions for [(E K)D]max and [(E K) β ]max in terms of 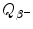 .
.(c)
Decay of a free (extra-nuclear) neutron into a proton p, electron e, and electronic anti-neutrino 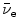 is the simplest example of β − decay. Calculate the Q value
is the simplest example of β − decay. Calculate the Q value 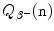 of a neutron undergoing β − decay. Appropriate rest energies of neutron, proton, and electron are available in Appendix A.
of a neutron undergoing β − decay. Appropriate rest energies of neutron, proton, and electron are available in Appendix A.
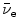 is the simplest example of β − decay. Calculate the Q value
is the simplest example of β − decay. Calculate the Q value 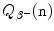 of a neutron undergoing β − decay. Appropriate rest energies of neutron, proton, and electron are available in Appendix A.
of a neutron undergoing β − decay. Appropriate rest energies of neutron, proton, and electron are available in Appendix A.(d)
For β − decay of neutron determine the maximum kinetic energy [(E K) β ]max of the ejected electron and the maximum recoil kinetic energy [(E K)D]max of the proton.
SOLUTION:
(a) Beta minus (β −) decay is characterized by a spontaneous transformation of a neutron into a proton in a neutron-rich nucleus concurrently with ejection of an electron and antineutrino
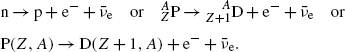
Similarly to the case of nuclear reaction and the case of α decay, the decay energy 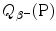 for beta minus decay can be determined either with (1) nuclear rest energy method or (2) atomic rest energy method.
for beta minus decay can be determined either with (1) nuclear rest energy method or (2) atomic rest energy method.
For the β − decay to occur, as stated in (11.42), 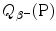 must be positive, and we conclude from (11.42) that, in terms of atomic masses, the atomic mass of the parent
must be positive, and we conclude from (11.42) that, in terms of atomic masses, the atomic mass of the parent 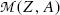 must exceed the atomic mass of the daughter
must exceed the atomic mass of the daughter 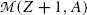 ; i.e.,
; i.e., 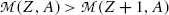 , in contrast consideration of nuclear masses where, as stated in (11.41), the rest mass of parent nucleus M(Z,A) must exceed the mass of the daughter nucleus M(Z+1,A) by more than one electron rest mass m e for β − decay to be feasible.
, in contrast consideration of nuclear masses where, as stated in (11.41), the rest mass of parent nucleus M(Z,A) must exceed the mass of the daughter nucleus M(Z+1,A) by more than one electron rest mass m e for β − decay to be feasible.
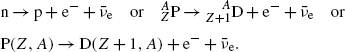
(11.40)
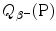 for beta minus decay can be determined either with (1) nuclear rest energy method or (2) atomic rest energy method.
for beta minus decay can be determined either with (1) nuclear rest energy method or (2) atomic rest energy method.(1)
In the nuclear rest energy method, one subtracts the sum of rest energies of decay products after the β − decay (daughter D, electron e−, and antineutrino 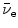 ) from the rest energy of the parent nucleus M(P)c 2. Decay energy
) from the rest energy of the parent nucleus M(P)c 2. Decay energy 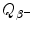 for the β − decay process must be positive for β − decay to occur and is given in terms of nuclear rest mass M as follows
for the β − decay process must be positive for β − decay to occur and is given in terms of nuclear rest mass M as follows
![$$ Q_{\beta^-}(\mathrm{P})= M(\mathrm{P})c^2-\sum _{i,\ \mathrm{after}}M_ic^2 =\bigl\{M(Z,A)- \bigl[M(Z+1,A)+m_{\mathrm{e}}+0\bigr]\bigr\}c^2, $$](/wp-content/uploads/2016/04/A212719_1_En_11_Chapter_Equ41.gif)
where the term in square brackets represents the sum of nuclear rest masses of decay products: daughter M(Z+1,A), electron m e, and 0 representing the rest mass of antineutrino. However, in terms of nuclear rest masses, the condition ![$Q_{\beta^{-}}>0$” src=”/wp-content/uploads/2016/04/A212719_1_En_11_Chapter_IEq32.gif”></SPAN> is a necessary but not sufficient condition for <SPAN class=EmphasisTypeItalic>β</SPAN> <SUP>−</SUP> decay to occur. As indicated in (<SPAN class=InternalRef><A href=]() 11.41), β − decay can occur to a neutron-rich unstable parent nucleus only when the mass M(Z,A) of the parent P nucleus exceeds the mass M(Z+1,A) of the daughter D nucleus by more than one electron rest mass m e, i.e., M(Z,A)>M(Z+1,A)+m e.
11.41), β − decay can occur to a neutron-rich unstable parent nucleus only when the mass M(Z,A) of the parent P nucleus exceeds the mass M(Z+1,A) of the daughter D nucleus by more than one electron rest mass m e, i.e., M(Z,A)>M(Z+1,A)+m e.
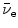 ) from the rest energy of the parent nucleus M(P)c 2. Decay energy
) from the rest energy of the parent nucleus M(P)c 2. Decay energy 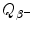 for the β − decay process must be positive for β − decay to occur and is given in terms of nuclear rest mass M as follows
for the β − decay process must be positive for β − decay to occur and is given in terms of nuclear rest mass M as follows![$$ Q_{\beta^-}(\mathrm{P})= M(\mathrm{P})c^2-\sum _{i,\ \mathrm{after}}M_ic^2 =\bigl\{M(Z,A)- \bigl[M(Z+1,A)+m_{\mathrm{e}}+0\bigr]\bigr\}c^2, $$](/wp-content/uploads/2016/04/A212719_1_En_11_Chapter_Equ41.gif)
(11.41)
(2)
Adding and subtracting Zm e c 2 to the right-hand side of (11.41) and neglecting the electron binding energies to the nucleus we obtain
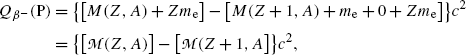
where 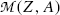 and
and 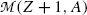 represent the atomic rest masses of the parent and daughter, respectively, noting that the following expressions link atomic and nuclear masses,
represent the atomic rest masses of the parent and daughter, respectively, noting that the following expressions link atomic and nuclear masses, 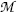 and M, respectively
and M, respectively
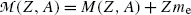
and
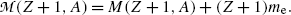
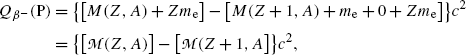
(11.42)
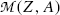 and
and 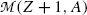 represent the atomic rest masses of the parent and daughter, respectively, noting that the following expressions link atomic and nuclear masses,
represent the atomic rest masses of the parent and daughter, respectively, noting that the following expressions link atomic and nuclear masses, 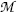 and M, respectively
and M, respectively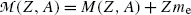
(11.43)
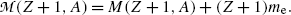
(11.44)
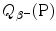 must be positive, and we conclude from (11.42) that, in terms of atomic masses, the atomic mass of the parent
must be positive, and we conclude from (11.42) that, in terms of atomic masses, the atomic mass of the parent 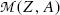 must exceed the atomic mass of the daughter
must exceed the atomic mass of the daughter 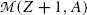 ; i.e.,
; i.e., 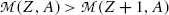 , in contrast consideration of nuclear masses where, as stated in (11.41), the rest mass of parent nucleus M(Z,A) must exceed the mass of the daughter nucleus M(Z+1,A) by more than one electron rest mass m e for β − decay to be feasible.
, in contrast consideration of nuclear masses where, as stated in (11.41), the rest mass of parent nucleus M(Z,A) must exceed the mass of the daughter nucleus M(Z+1,A) by more than one electron rest mass m e for β − decay to be feasible.(b) Expressions for maximum kinetic energy [(E K) β ]max of the electron ejected in β − decay were derived in Prob. 227 (11.37) and can be restated in relativistic format as follows
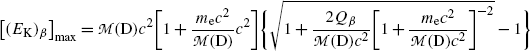
and, after recognizing that 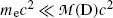 , (11.45) is simplified greatly to read
, (11.45) is simplified greatly to read
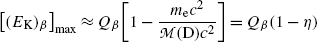
and provides the following result for maximum recoil kinetic energy [(E K)D]max of the daughter
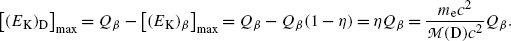
(c) Decay energy 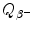 of neutron undergoing β − decay is calculated using either the nuclear rest energy method of (11.41) or atomic rest energy method of (11.42). In the nuclear energy method the rest energy of the parent (neutron) must exceed the rest energy of the daughter (proton) by more than one electronic rest mass m e c 2=0.5110 MeV.
of neutron undergoing β − decay is calculated using either the nuclear rest energy method of (11.41) or atomic rest energy method of (11.42). In the nuclear energy method the rest energy of the parent (neutron) must exceed the rest energy of the daughter (proton) by more than one electronic rest mass m e c 2=0.5110 MeV.
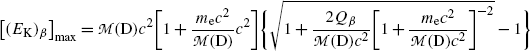
(11.45)
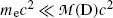 , (11.45) is simplified greatly to read
, (11.45) is simplified greatly to read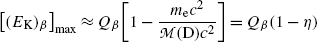
(11.46)
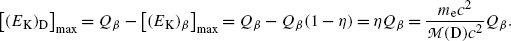
(11.47)
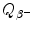 of neutron undergoing β − decay is calculated using either the nuclear rest energy method of (11.41) or atomic rest energy method of (11.42). In the nuclear energy method the rest energy of the parent (neutron) must exceed the rest energy of the daughter (proton) by more than one electronic rest mass m e c 2=0.5110 MeV.
of neutron undergoing β − decay is calculated using either the nuclear rest energy method of (11.41) or atomic rest energy method of (11.42). In the nuclear energy method the rest energy of the parent (neutron) must exceed the rest energy of the daughter (proton) by more than one electronic rest mass m e c 2=0.5110 MeV.As shown in Appendix A, M(Z,A)c 2=m n c 2=939.5654 MeV and M(Z+1,A)c 2=m p c 2=938.2720 MeV, leading us to the conclusion that the parent nucleus (neutron) rest energy exceeds the daughter nucleus (proton) rest energy by 1.2934 MeV, an amount larger that the minimum of one electron rest mass required for β − decay to be feasible.
(1) Using the nuclear rest energy method (11.41) we obtain the following result for 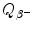
![$$\begin{aligned} Q_{\beta^-}(\mathrm{n}) =& \bigl\{M(Z,A)-\bigl[M(Z+1,A)+m_{\mathrm{e}} \bigr]\bigr\} =m_{\mathrm{n}}c^2-m_{\mathrm{p}}c^2-m_{\mathrm{e}}c^2 \\ =&939.5654~\mathrm{MeV}-938.2720~\mathrm{MeV}-0.5110~\mathrm{MeV}= 0.7824~ \mathrm{MeV}. \end{aligned}$$](/wp-content/uploads/2016/04/A212719_1_En_11_Chapter_Equ48.gif)
(2) Same result will be obtained using the atomic rest energy method (11.42) by assuming that the daughter product is the hydrogen atom
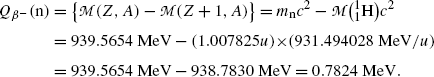
(d) Maximum kinetic energy [(E K) β ]max of the beta particle and maximum recoil energy [(E K)D]max of the daughter nucleus are calculated from (11.46) and (11.47), respectively, as follows
![$$\begin{aligned} \bigl[(E_{\mathrm{K}})_{\beta}\bigr]_{\max} =&Q_{\beta^-}( \mathrm{n}) \biggl[1-\frac{m_{\mathrm{e}}c^2}{m_{\mathrm{p}}c^2}\biggr]= (0.7824~\mathrm{MeV}){\times} \biggl[1-\frac{0.5110}{938.272}\biggr] \\ =&0.7820~\mathrm{MeV} \end{aligned}$$](/wp-content/uploads/2016/04/A212719_1_En_11_Chapter_Equ50.gif)
and
![$$\begin{aligned} \bigl[(E_{\mathrm{K}})_{\mathrm{D}} \bigr]_{\max} =& Q_{\beta^-}(\mathrm{n})- \bigl[(E_{\mathrm{K}})_{\beta} \bigr]_{\max} =Q_{\beta^-}(\mathrm{n}) \biggl[\frac{m_{\mathrm{e}}c^2}{m_{\mathrm{p}}c^2}\biggr] \\ =&(0.7824~\mathrm{MeV}){\times}\biggl[\frac{0.5110}{938.272}\biggr]=4{\times} 10^{-4}~\mathrm{MeV}. \end{aligned}$$](/wp-content/uploads/2016/04/A212719_1_En_11_Chapter_Equ51.gif)
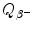
![$$\begin{aligned} Q_{\beta^-}(\mathrm{n}) =& \bigl\{M(Z,A)-\bigl[M(Z+1,A)+m_{\mathrm{e}} \bigr]\bigr\} =m_{\mathrm{n}}c^2-m_{\mathrm{p}}c^2-m_{\mathrm{e}}c^2 \\ =&939.5654~\mathrm{MeV}-938.2720~\mathrm{MeV}-0.5110~\mathrm{MeV}= 0.7824~ \mathrm{MeV}. \end{aligned}$$](/wp-content/uploads/2016/04/A212719_1_En_11_Chapter_Equ48.gif)
(11.48)
(11.49)
![$$\begin{aligned} \bigl[(E_{\mathrm{K}})_{\beta}\bigr]_{\max} =&Q_{\beta^-}( \mathrm{n}) \biggl[1-\frac{m_{\mathrm{e}}c^2}{m_{\mathrm{p}}c^2}\biggr]= (0.7824~\mathrm{MeV}){\times} \biggl[1-\frac{0.5110}{938.272}\biggr] \\ =&0.7820~\mathrm{MeV} \end{aligned}$$](/wp-content/uploads/2016/04/A212719_1_En_11_Chapter_Equ50.gif)
(11.50)
![$$\begin{aligned} \bigl[(E_{\mathrm{K}})_{\mathrm{D}} \bigr]_{\max} =& Q_{\beta^-}(\mathrm{n})- \bigl[(E_{\mathrm{K}})_{\beta} \bigr]_{\max} =Q_{\beta^-}(\mathrm{n}) \biggl[\frac{m_{\mathrm{e}}c^2}{m_{\mathrm{p}}c^2}\biggr] \\ =&(0.7824~\mathrm{MeV}){\times}\biggl[\frac{0.5110}{938.272}\biggr]=4{\times} 10^{-4}~\mathrm{MeV}. \end{aligned}$$](/wp-content/uploads/2016/04/A212719_1_En_11_Chapter_Equ51.gif)
(11.51)
In neutron β − decay the proton (daughter product) acquires only a minute fraction that amounts to at most [(E K)D]max=4×10−4 MeV of the total decay energy 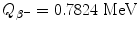 . The rest of the decay energy (0.7820 MeV) is carried away by the ejected beta particle and antineutrino in random proportions; however, the sum of kinetic energies carried by the two particles (electron and neutrino) must be equal to the maximum kinetic energy available for the two particles [(E K) β ]max=0.7820 MeV. Note: Kinetic energy of the two particles (0.7820 MeV) plus recoil kinetic energy of the daughter product (0.0004 MeV) is equal to the decay energy
. The rest of the decay energy (0.7820 MeV) is carried away by the ejected beta particle and antineutrino in random proportions; however, the sum of kinetic energies carried by the two particles (electron and neutrino) must be equal to the maximum kinetic energy available for the two particles [(E K) β ]max=0.7820 MeV. Note: Kinetic energy of the two particles (0.7820 MeV) plus recoil kinetic energy of the daughter product (0.0004 MeV) is equal to the decay energy 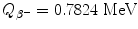 .
.
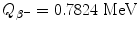 . The rest of the decay energy (0.7820 MeV) is carried away by the ejected beta particle and antineutrino in random proportions; however, the sum of kinetic energies carried by the two particles (electron and neutrino) must be equal to the maximum kinetic energy available for the two particles [(E K) β ]max=0.7820 MeV. Note: Kinetic energy of the two particles (0.7820 MeV) plus recoil kinetic energy of the daughter product (0.0004 MeV) is equal to the decay energy
. The rest of the decay energy (0.7820 MeV) is carried away by the ejected beta particle and antineutrino in random proportions; however, the sum of kinetic energies carried by the two particles (electron and neutrino) must be equal to the maximum kinetic energy available for the two particles [(E K) β ]max=0.7820 MeV. Note: Kinetic energy of the two particles (0.7820 MeV) plus recoil kinetic energy of the daughter product (0.0004 MeV) is equal to the decay energy 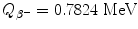 .
.11.4.Q2 (229)
Most notable β − emitters of significance in medical physics are: cobalt-60  , cesium-137
, cesium-137  , and europium-152
, and europium-152 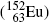 as radiation sources for external beam radiotherapy and iodine-131
as radiation sources for external beam radiotherapy and iodine-131 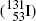 for thyroid nuclear imaging and thyroid ablation.
for thyroid nuclear imaging and thyroid ablation.
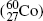 , cesium-137
, cesium-137 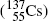 , and europium-152
, and europium-152 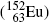 as radiation sources for external beam radiotherapy and iodine-131
as radiation sources for external beam radiotherapy and iodine-131 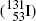 for thyroid nuclear imaging and thyroid ablation.
for thyroid nuclear imaging and thyroid ablation.Calculate for the following radionuclides:
(1)
Cobalt-60.
(2)
Iodine-131.
(3)
Cesium-137.
(4)
Europium-152.
(a)
Specific activity a.
(b)
Binding energy per nucleon E B/A.
(c)
Decay energy 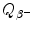 . Use both the atomic and nuclear rest energy method in the calculation of
. Use both the atomic and nuclear rest energy method in the calculation of 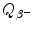 . Appropriate nuclear and atomic data are provided in Appendix A.
. Appropriate nuclear and atomic data are provided in Appendix A.
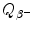 . Use both the atomic and nuclear rest energy method in the calculation of
. Use both the atomic and nuclear rest energy method in the calculation of 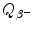 . Appropriate nuclear and atomic data are provided in Appendix A.
. Appropriate nuclear and atomic data are provided in Appendix A.(d)
Summarize in a tabular format your results obtained in (a), (b), and (c).
SOLUTION:
(a) Specific activity a of a radionuclide is defined as activity 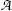 per unit mass m
per unit mass m
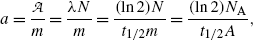
where, for a given radionuclide, λ is the decay constant [λ=(ln2)/t 1/2] with t 1/2 the half-life, N A is the Avogadro number (6.022×1023 mol−1), and A is the atomic mass. From (11.52) we note that specific activity a is inversely proportional to both the half-life t 1/2 as well as atomic mass A.
(b) The sum of masses of individual components of a nucleus that contains Z protons and A−Z neutrons is larger than the actual mass of the nucleus. This difference in mass is called the mass defect (deficit) Δm and its energy equivalent Δmc 2 is called the total binding energy E B of the given nucleus (Z,A). The binding energy per nucleon E B/A of a nucleus, i.e., the total binding energy of a nucleus E B divided by the number of nucleons A, varies with the number of nucleons, is of the order of ∼8 MeV/nucleon, and is determined as follows
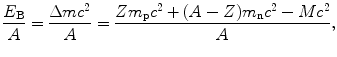
where m p c 2 is the proton rest energy (938.272013 MeV), m n c 2 is the neutron rest energy (939.565346 MeV), and Mc 2 is the rest energy of nucleus (Z,A).
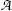 per unit mass m
per unit mass m
(11.52)
(1)
Specific activity a of cobalt-60 (t 1/2=5.26 a):
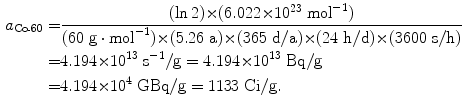
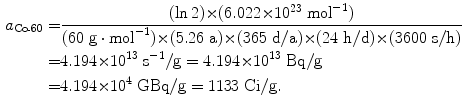
(11.53)
(2)
Specific activity a of iodine-131 (t 1/2=8.02 d):
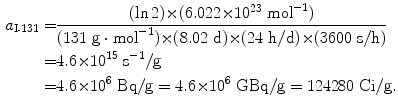
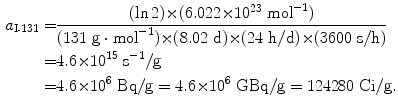
(11.54)
(3)
Specific activity a of cesium-137 (t 1/2=30 a)
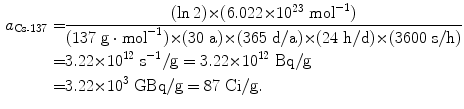
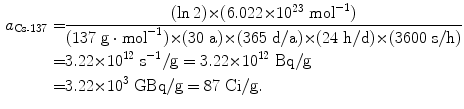
(11.55)
(4)
Specific activity a of europium-152 (t 1/2=13.52 a):
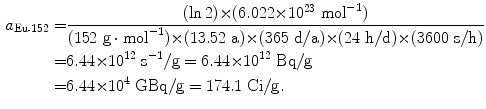
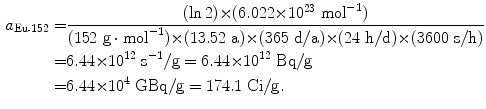
(11.56)
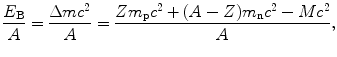
(11.57)
(1)
Binding energy per nucleon of cobalt-60 (Z=27, A=60):
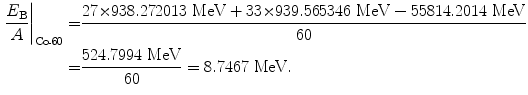
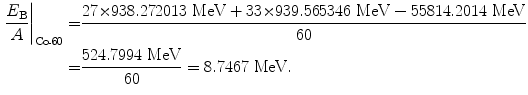
(11.58)
(2)
Binding energy per nucleon of iodine-131 (Z=53, A=131):
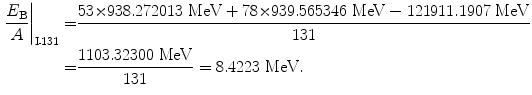
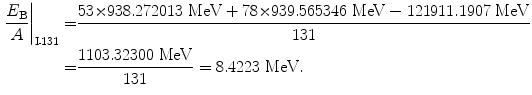
(11.59)
(3)
Binding energy per nucleon of cesium-137 (Z=55, A=137):
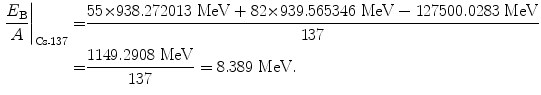
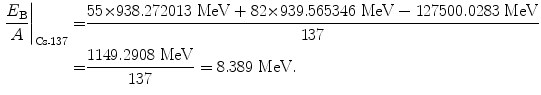
(11.60)
(4)
Binding energy per nucleon of europium-152 (Z=63, A=152):
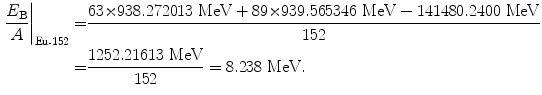
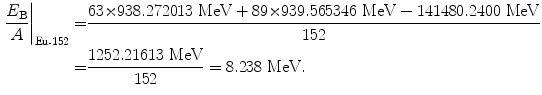
(11.61)
Figure 11.3 plots binding energy per nucleon against atomic mass number A in the range of A from 1 to 250. Results calculated in (b) for Co-60, I-131, Cs-137, and Eu-152 are also shown. In general, the larger is the binding energy per nucleon E B/A of an atom, the larger is the stability of its nucleus. Thus, the most stable nuclei in nature are the ones with A≈60 (iron, cobalt, and nickel).
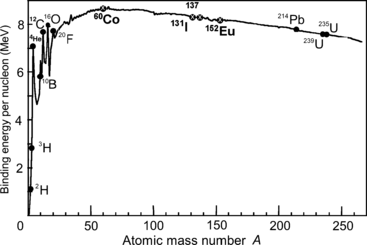

Fig. 11.3
Binding energy per nucleon E B/A in MeV/nucleon against atomic mass number A
(c) Beta minus Q value also known as β − decay energy 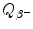 can be determined either with the atomic rest energy method or with the nuclear rest energy method, which, respectively, can be expressed as follows
can be determined either with the atomic rest energy method or with the nuclear rest energy method, which, respectively, can be expressed as follows
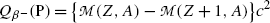
and
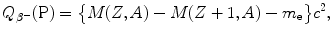
where P stands for parent nucleus with atomic number Z and atomic mass number A, M stands for nuclear rest mass, 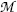 stands for atomic rest mass, and m e is the rest mass of the electron.
stands for atomic rest mass, and m e is the rest mass of the electron.
Beta minus decay energy 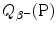 was calculated for four radionuclides (Co-60, I-131, Cs-137, and Eu-152) that decay with β − decay and are of importance in medical physics, three of them (Co-60, Cs-137, and Eu-152) as radiation sources for external beam radiotherapy and I-131 for thyroid imaging or ablation. Europium-152 has not been used clinically yet, however, studies have shown its potential usefulness as radiation source. In addition to β − decay (27.9 %), Eu-152 also decays with electron capture (72.1 %) and β + decay (0.03 %). The other three radionuclides decay only through β − decay (100 %).
was calculated for four radionuclides (Co-60, I-131, Cs-137, and Eu-152) that decay with β − decay and are of importance in medical physics, three of them (Co-60, Cs-137, and Eu-152) as radiation sources for external beam radiotherapy and I-131 for thyroid imaging or ablation. Europium-152 has not been used clinically yet, however, studies have shown its potential usefulness as radiation source. In addition to β − decay (27.9 %), Eu-152 also decays with electron capture (72.1 %) and β + decay (0.03 %). The other three radionuclides decay only through β − decay (100 %).
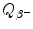 can be determined either with the atomic rest energy method or with the nuclear rest energy method, which, respectively, can be expressed as follows
can be determined either with the atomic rest energy method or with the nuclear rest energy method, which, respectively, can be expressed as follows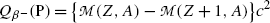
(11.62)
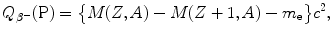
(11.63)
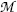 stands for atomic rest mass, and m e is the rest mass of the electron.
stands for atomic rest mass, and m e is the rest mass of the electron.(1)
Beta minus decay energy 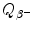 for cobalt-60 decay into nickel-60 (t 1/2=5.26 a)
for cobalt-60 decay into nickel-60 (t 1/2=5.26 a)
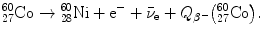
Atomic rest energy method
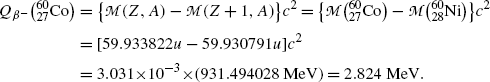
Nuclear rest energy method
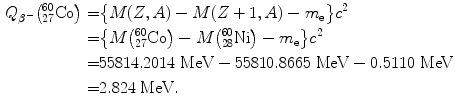
 for cobalt-60 decay into nickel-60 (t 1/2=5.26 a)
for cobalt-60 decay into nickel-60 (t 1/2=5.26 a)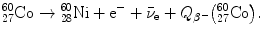
(11.64)
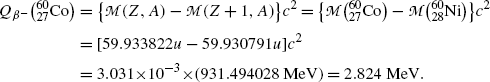
(11.65)
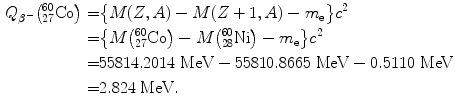
(11.66)
(2)
Beta minus decay energy 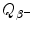 for iodine-131 decay into xenon-131 (t 1/2=8.02 d)
for iodine-131 decay into xenon-131 (t 1/2=8.02 d)
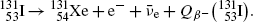
Atomic rest energy method
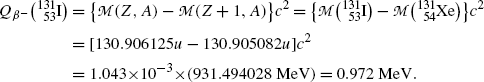
Nuclear rest energy method
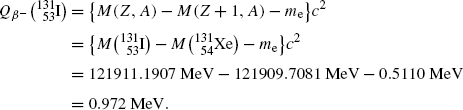
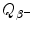 for iodine-131 decay into xenon-131 (t 1/2=8.02 d)
for iodine-131 decay into xenon-131 (t 1/2=8.02 d)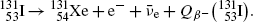
(11.67)
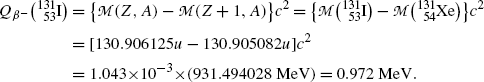
(11.68)
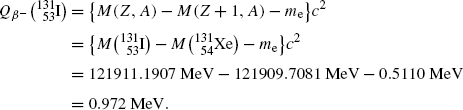
(11.69)
(3)
Beta minus decay energy 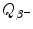 for cesium-137 decay into barium-137 (t 1/2=30 a)
for cesium-137 decay into barium-137 (t 1/2=30 a)
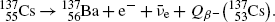
Atomic rest energy method
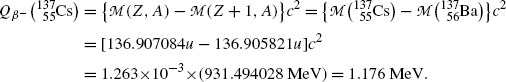
Nuclear rest energy method
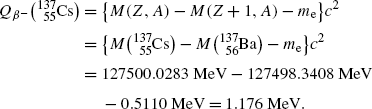
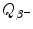 for cesium-137 decay into barium-137 (t 1/2=30 a)
for cesium-137 decay into barium-137 (t 1/2=30 a)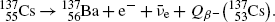
(11.70)
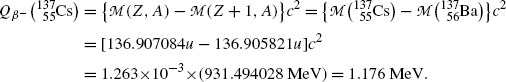
(11.71)
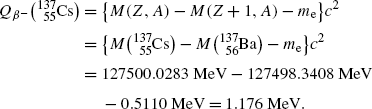
(11.72)
(4)
Beta minus decay energy 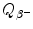 for europium-152 decay into gadolinium-152 (t 1/2=13.52 a)
for europium-152 decay into gadolinium-152 (t 1/2=13.52 a)
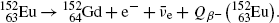
Atomic rest energy method
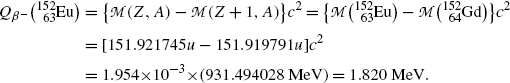
Nuclear rest energy method
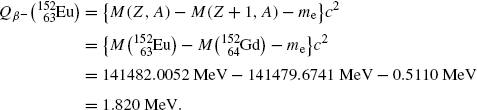
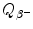 for europium-152 decay into gadolinium-152 (t 1/2=13.52 a)
for europium-152 decay into gadolinium-152 (t 1/2=13.52 a)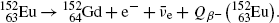
(11.73)
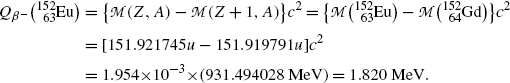
(11.74)
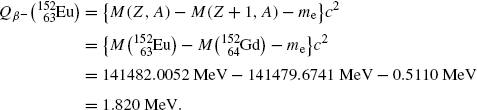
(11.75)
 was calculated for four radionuclides (Co-60, I-131, Cs-137, and Eu-152) that decay with β − decay and are of importance in medical physics, three of them (Co-60, Cs-137, and Eu-152) as radiation sources for external beam radiotherapy and I-131 for thyroid imaging or ablation. Europium-152 has not been used clinically yet, however, studies have shown its potential usefulness as radiation source. In addition to β − decay (27.9 %), Eu-152 also decays with electron capture (72.1 %) and β + decay (0.03 %). The other three radionuclides decay only through β − decay (100 %).
was calculated for four radionuclides (Co-60, I-131, Cs-137, and Eu-152) that decay with β − decay and are of importance in medical physics, three of them (Co-60, Cs-137, and Eu-152) as radiation sources for external beam radiotherapy and I-131 for thyroid imaging or ablation. Europium-152 has not been used clinically yet, however, studies have shown its potential usefulness as radiation source. In addition to β − decay (27.9 %), Eu-152 also decays with electron capture (72.1 %) and β + decay (0.03 %). The other three radionuclides decay only through β − decay (100 %).Decay energies  for the four radionuclides were calculated with the atomic rest energy method and with the nuclear rest energy method. For a given radionuclide both methods gave identical results, as shown above.
for the four radionuclides were calculated with the atomic rest energy method and with the nuclear rest energy method. For a given radionuclide both methods gave identical results, as shown above.
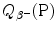 for the four radionuclides were calculated with the atomic rest energy method and with the nuclear rest energy method. For a given radionuclide both methods gave identical results, as shown above.
for the four radionuclides were calculated with the atomic rest energy method and with the nuclear rest energy method. For a given radionuclide both methods gave identical results, as shown above.(d) Summary of results on specific activity a, binding energy per nucleon E B/A, and β − decay energy 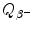 for radionuclides: cobalt-60, iodine-131, cesium-137, and europium-152 is presented in Table 11.2.
for radionuclides: cobalt-60, iodine-131, cesium-137, and europium-152 is presented in Table 11.2.
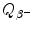 for radionuclides: cobalt-60, iodine-131, cesium-137, and europium-152 is presented in Table 11.2.
for radionuclides: cobalt-60, iodine-131, cesium-137, and europium-152 is presented in Table 11.2.Table 11.2
Various nuclear parameters for four radionuclides of importance to medical physics
(1) | Radionuclide | Specific activity a (Ci/g) | Binding energy per nucleon E B/A (MeV) | Beta minus decay energy 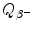 (MeV) (MeV) |
|---|---|---|---|---|
(2) | Cobalt-60 | 1133 | 8.75 | 2.824 |
(3) | Iodine-131 | 124280 | 8.42 | 0.972 |
(4) | Cesium-137 | 87 | 8.39 | 1.176 |
(5) | Europium-152 | 174 | 8.24 | 1.820 |
11.5 Beta Plus Decay
11.5.Q1 (230)
Beta plus (β +) decay is characterized by the production of positrons that appear in a spectral distribution with maximum positron energy specific to the particular β + decay. As in the β − decay, the daughter recoil kinetic energy in β + decay is essentially negligible. Radionuclides undergoing β + decay are often called positron emitters and are used in medicine for functional imaging with a special imaging technique called positron emission tomography (PET).
(a)
List at least 5 positron emitting radionuclides that can be attached to biological markers and used in PET imaging.
(b)
Briefly discuss the main characteristics of PET imaging:
(1)
Information that it provides.
(2)
Production of radionuclides for use in PET studies.
(3)
Acquisition of PET scans.
(c)
State expressions for β + decay energy 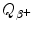 (Q value of β + decay) based on:
(Q value of β + decay) based on:
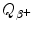 (Q value of β + decay) based on:
(Q value of β + decay) based on:(1)
Nuclear rest energy of parent P and daughter D.
(2)
Atomic rest energy of parent P and daughter D.
(d)
Show a schematic representation of a typical radioactive beta plus β + decay transition from a parent nucleus P(Z,A) to ground state of a daughter nucleus D(Z−1,A) based on:
Appropriate atomic and nuclear data are available from Appendix A. Show the correspondence between the two graphs.
(1)
Atomic rest energies.
(2)
Nuclear rest energies.
SOLUTION:
The most frequently used positron emitters are: carbon-11 (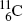 ); nitrogen-13 (
); nitrogen-13 (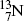 ); oxygen-15 (
); oxygen-15 (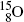 ); fluorine-18 (
); fluorine-18 (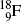 ); and rubidium-82 (
); and rubidium-82 (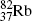 ).
).
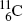 ); nitrogen-13 (
); nitrogen-13 (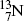 ); oxygen-15 (
); oxygen-15 (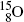 ); fluorine-18 (
); fluorine-18 (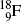 ); and rubidium-82 (
); and rubidium-82 (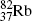 ).
).Of these, fluorine-18 is the most frequently used radionuclide in PET scanning. It is applied for labeling the deoxyglucose biological marker thereby forming the radiopharmaceutical fluorodeoxyglucose (FDG) for use in studies involving glucose metabolism in cancer diagnosis.
(b) Main characteristics of PET imaging are as follows:
(c) Beta plus (β +) decay is characterized by a spontaneous transformation of a proton into a neutron in a proton-rich nucleus concurrently with ejection of a positron and electronic neutrino
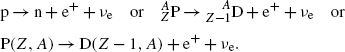
Similarly to the case of nuclear reaction, α decay, and β − decay, the decay energy 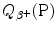 for beta plus decay can be determined either with (1) nuclear rest energy method or (2) atomic rest energy method.
for beta plus decay can be determined either with (1) nuclear rest energy method or (2) atomic rest energy method.
(d) From (11.77) and (11.78) we note that 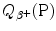 can be expressed in terms of nuclear masses M or in terms of atomic masses
can be expressed in terms of nuclear masses M or in terms of atomic masses 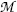 of parent P(Z,A) and daughter D(Z−1,A) as follows
of parent P(Z,A) and daughter D(Z−1,A) as follows
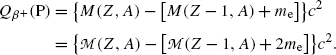
(1)
PET is a nuclear medicine molecular imaging technique that provides information on metabolic function of organs or tissues by detecting how cells process certain compounds such as, for example, glucose. Cancer cells metabolize glucose at a much higher rate than normal tissues. By detecting increased radiolabelled glucose metabolism with a high degree of sensitivity, PET identifies cancerous cells, even at an early stage when other imaging modalities may miss them.
(2)
The radionuclides used in PET studies are most commonly produced by bombardment of an appropriate stable nuclide with protons from a cyclotron thereby producing positron-emitting radionuclides that are subsequently used for labeling biochemical substances and producing radioactive tracers. Another means of production of proton-rich radionuclides is by using a suitable generator, such as, for example, a rubidium-82 generator containing strontium-82 that decays by electron capture into positron emitting rubidium-82.
(3)
In a PET study one administers a positron-emitting radionuclide by injection or inhalation. The radionuclide circulates through the bloodstream to reach a particular organ. The positrons emitted by the radionuclide have a very short range in tissue (of the order of 1 mm) and undergo annihilation with an available atomic orbital electron typically at the end of their tracks. This process generally results in emission of two gamma photons called annihilation quanta, each with energy of 0.511 MeV, moving away from the point of production in nearly opposite directions.
(4)
Decay events are detected by coincidence detection of the annihilation quanta with a timing window of the order of few nanoseconds. Typical detectors are scintillators coupled with a photomultiplier tube (PMT) or photodiode and arranged in a ring about the patient. The line connecting the two detectors triggered in coincidence is called the coincidence line and many such lines are formed during acquisition of a PET scan. Spatial activity distribution in the organ of interest within the field-of-view is reconstructed from the measured projections with the help of mathematical algorithms.
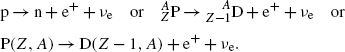
(11.76)
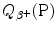 for beta plus decay can be determined either with (1) nuclear rest energy method or (2) atomic rest energy method.
for beta plus decay can be determined either with (1) nuclear rest energy method or (2) atomic rest energy method.(1)
In the nuclear rest energy method, one subtracts the sum of rest energies of decay products after the β + decay (daughter D, positron e+, and electronic neutrino ν e) from the rest energy of the parent nucleus M(P)c 2. Decay energy 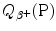 for the β + decay process must be positive for β + decay to occur and is given in terms of nuclear rest mass M as follows
for the β + decay process must be positive for β + decay to occur and is given in terms of nuclear rest mass M as follows
![$$ Q_{\beta ^{ +}} (\mathrm{P}) = M(\mathrm{P})c^{2} - \sum _{i} M_{i} c^{2} = \bigl\{ M(Z,A) - \bigl[M(Z - 1,A) + m_{\mathrm{e}} + 0\bigr]\bigr\} c^{2}, $$](/wp-content/uploads/2016/04/A212719_1_En_11_Chapter_Equ77.gif)
where the term in square brackets represents the sum of nuclear rest masses of decay products: daughter M(Z−1,A), positron m e, and 0 representing the rest mass of neutrino. However, in terms of nuclear rest masses, the condition ![$Q_{\beta ^{ +}} > 0$” src=”/wp-content/uploads/2016/04/A212719_1_En_11_Chapter_IEq70.gif”></SPAN> is a necessary but not sufficient condition for <SPAN class=EmphasisTypeItalic>β</SPAN> <SUP>+</SUP> decay to occur.</DIV><br />
<DIV class=Para>As indicated in (<SPAN class=InternalRef><A href=]() 11.77), β + decay can occur to a proton-rich unstable parent nucleus only when the mass M(Z,A) of the parent P nucleus exceeds the mass M(Z−1,A) of the daughter D nucleus by more than one positron rest mass m e, i.e., M(Z,A)>M(Z−1,A)+m e.
11.77), β + decay can occur to a proton-rich unstable parent nucleus only when the mass M(Z,A) of the parent P nucleus exceeds the mass M(Z−1,A) of the daughter D nucleus by more than one positron rest mass m e, i.e., M(Z,A)>M(Z−1,A)+m e.
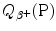 for the β + decay process must be positive for β + decay to occur and is given in terms of nuclear rest mass M as follows
for the β + decay process must be positive for β + decay to occur and is given in terms of nuclear rest mass M as follows![$$ Q_{\beta ^{ +}} (\mathrm{P}) = M(\mathrm{P})c^{2} - \sum _{i} M_{i} c^{2} = \bigl\{ M(Z,A) - \bigl[M(Z - 1,A) + m_{\mathrm{e}} + 0\bigr]\bigr\} c^{2}, $$](/wp-content/uploads/2016/04/A212719_1_En_11_Chapter_Equ77.gif)
(11.77)
(2)
Adding and subtracting Zm e c 2 to the right-hand side of (11.77) and neglecting the electron binding energies to the nucleus we obtain the following expression for 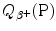 for the atomic rest energy method
for the atomic rest energy method
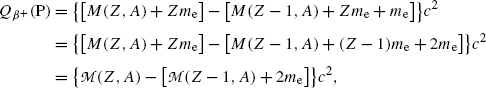
where M(Z,A) and M(Z−1,A) stand for nuclear rest masses of the parent and daughter, respectively, and 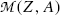 and
and 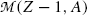 stand for atomic rest masses of the parent and daughter, respectively, noting that the following expressions link atomic and nuclear masses,
stand for atomic rest masses of the parent and daughter, respectively, noting that the following expressions link atomic and nuclear masses, 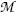 and M, respectively
and M, respectively
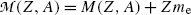
and
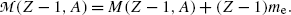
From (11.78) a conclusion can be made that, for β + decay to occur, the atomic mass of the parent 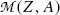 must exceed the atomic mass of the daughter
must exceed the atomic mass of the daughter 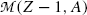 by more than two positron rest masses, or, in terms of rest energies
by more than two positron rest masses, or, in terms of rest energies
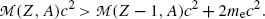
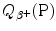 for the atomic rest energy method
for the atomic rest energy method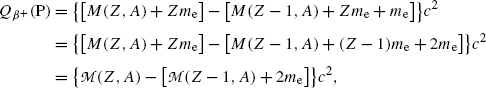
(11.78)
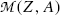 and
and 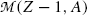 stand for atomic rest masses of the parent and daughter, respectively, noting that the following expressions link atomic and nuclear masses,
stand for atomic rest masses of the parent and daughter, respectively, noting that the following expressions link atomic and nuclear masses, 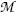 and M, respectively
and M, respectively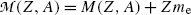
(11.79)
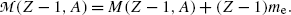
(11.80)
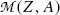 must exceed the atomic mass of the daughter
must exceed the atomic mass of the daughter 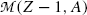 by more than two positron rest masses, or, in terms of rest energies
by more than two positron rest masses, or, in terms of rest energies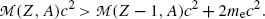
(11.81)
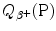 can be expressed in terms of nuclear masses M or in terms of atomic masses
can be expressed in terms of nuclear masses M or in terms of atomic masses 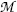 of parent P(Z,A) and daughter D(Z−1,A) as follows
of parent P(Z,A) and daughter D(Z−1,A) as follows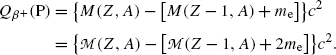
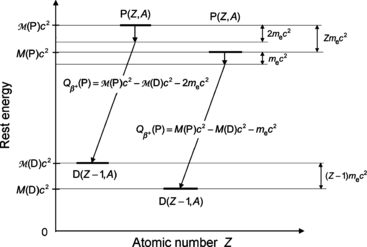
(11.82)
A schematic diagram of β + decay is shown in Fig. 11.4 using atomic masses on the left and nuclear masses on the right for the parent P(Z,A) and daughter D(Z−1,A). Of course, both methods must yield identical results for 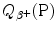 , as evident from the two energy level diagrams in Fig. 11.4. The magnitude of
, as evident from the two energy level diagrams in Fig. 11.4. The magnitude of 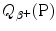 resulting from the atomic rest energy method in the left diagram is identical to that resulting from the nuclear rest energy method shown in the right diagram.
resulting from the atomic rest energy method in the left diagram is identical to that resulting from the nuclear rest energy method shown in the right diagram.
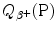 , as evident from the two energy level diagrams in Fig. 11.4. The magnitude of
, as evident from the two energy level diagrams in Fig. 11.4. The magnitude of 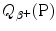 resulting from the atomic rest energy method in the left diagram is identical to that resulting from the nuclear rest energy method shown in the right diagram.
resulting from the atomic rest energy method in the left diagram is identical to that resulting from the nuclear rest energy method shown in the right diagram.
Fig. 11.4
Schematic diagram for β + decay; atomic rest energy on the left and nuclear rest energy on the right
11.5.Q2 (231)
The most frequently used positron emitters in clinical studies with PET scanners are: carbon-11 (C-11), nitrogen-13 (N-13), oxygen-15 (O-15), fluorine-18 (F-18), and rubidium-82 (Rb-82).
Get Clinical Tree app for offline access
(a)
Determine the beta plus decay energy 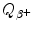 (also known as the Q value for β + decay) for the five most frequently used positron emitters: C-11, N-13, O-15, F-18, and Rb-82. In your calculation of
(also known as the Q value for β + decay) for the five most frequently used positron emitters: C-11, N-13, O-15, F-18, and Rb-82. In your calculation of 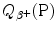 use both the atomic rest energy method as well as the nuclear rest energy method and convince yourself that both methods provide the identical results for a given radionuclide. Appropriate atomic and nuclear data are provided in Appendix A.
use both the atomic rest energy method as well as the nuclear rest energy method and convince yourself that both methods provide the identical results for a given radionuclide. Appropriate atomic and nuclear data are provided in Appendix A.
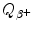 (also known as the Q value for β + decay) for the five most frequently used positron emitters: C-11, N-13, O-15, F-18, and Rb-82. In your calculation of
(also known as the Q value for β + decay) for the five most frequently used positron emitters: C-11, N-13, O-15, F-18, and Rb-82. In your calculation of 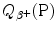 use both the atomic rest energy method as well as the nuclear rest energy method and convince yourself that both methods provide the identical results for a given radionuclide. Appropriate atomic and nuclear data are provided in Appendix A.
use both the atomic rest energy method as well as the nuclear rest energy method and convince yourself that both methods provide the identical results for a given radionuclide. Appropriate atomic and nuclear data are provided in Appendix A.(b)
Determine the maximum energy [(E K) β ]max of the positron emitted in β + decay of positron emitters listed in (a).
(c)
Prepare a table in which you list for the 5 most frequently used positron emitters of (a) and (b) the following parameters: Row (1): positron emitter; row (2): atomic number Z; row (3): atomic mass number A; row (4): half-life t 1/2; row (5): daughter product; row (6): decay energy 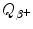 ; row (7): maximum positron energy [(E K) β ]max
; row (7): maximum positron energy [(E K) β ]max




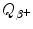 ; row (7): maximum positron energy [(E K) β ]max
; row (7): maximum positron energy [(E K) β ]max
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree