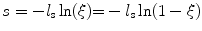(3.1)
where N(d) is the number of the unscattered photons at depth d, and N(0) is the number of incident photons [3].
For a given number of photons incident to a turbid medium the free path length between two consecutive interactions of the photons is given as
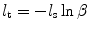
where 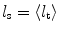 is the time averaged scattering mean free path length , and β is a random number which is evenly chosen between 0 and 1 and satisfies the probability function in (3.1).
is the time averaged scattering mean free path length , and β is a random number which is evenly chosen between 0 and 1 and satisfies the probability function in (3.1).
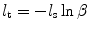
(3.2)
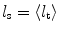 is the time averaged scattering mean free path length , and β is a random number which is evenly chosen between 0 and 1 and satisfies the probability function in (3.1).
is the time averaged scattering mean free path length , and β is a random number which is evenly chosen between 0 and 1 and satisfies the probability function in (3.1).In the Monte Carlo model developed for microscopic imaging systems [3], five independent variables are needed in order to simulate a multi-dimensional photon distribution; these include three spatial coordinates x, y, and z and two angular coordinates (a polar angle, θ and an azimuthal angle, ϕ). Figure 3.1 illustrates the coordinate system for a spherical scattering particle. These five independent variables are not necessarily set to zero for a microscopic imaging system and the method used for determining their initial values is outlined in Sect. 3.2.
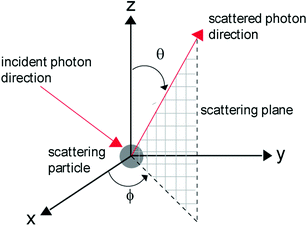

Fig. 3.1
Light scattering by a spherical particle
Each time a photon interacts with a scattering particle in the simulation model, new coordinates are determined. The new polar angle, θ, is equated to the scattering angle, θ s, which is chosen based on the Henyey–Greenstein (H–G) probability distribution [5]
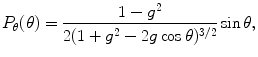
where g is the anisotropy value, calculated from (2.9). The scattering polar angle, θ s, can therefore be obtained from [5]
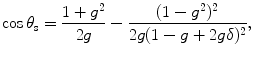
where δ is another evenly distributed random number from 0 to 1. The new azimuthal angle, ϕ, is randomly chosen between 0 and 2π, while the spatial coordinates, x, y, and z are determined by the sample and illumination conditions. In Sect. 3.3, we will describe the detail of photons migration through a layer of a turbid medium.
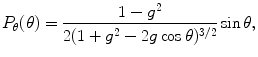
(3.3)
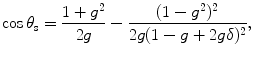
(3.4)
3.2 Microscopic Imaging
Because of the angular distribution of propagating photons through an objective in a microscope (see Fig. 3.2), the initial values of the three spatial coordinates x, y, and z and two angular coordinates θ and ϕ for a photon entering a turbid medium are not necessarily set to be 0. Figure 3.2 illustrates the geometric arrangement between the incident photons originating from a thin lens and a turbid medium. The origin, O, of the x–y–z coordinate system is defined as the point on the outer surface of the turbid medium that aligns through the focus and the center of the lens. With this convention the penetration depth, d′, into the turbid sample can be directly determined.
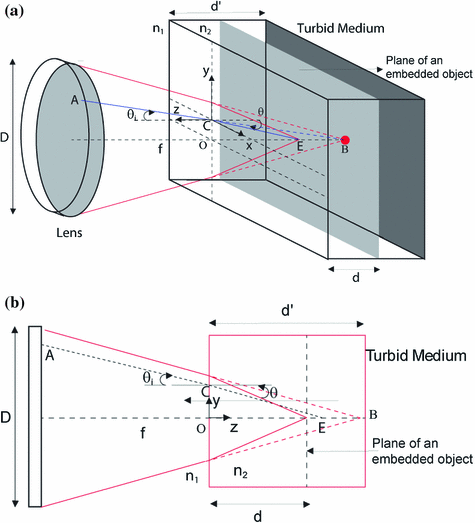

Fig. 3.2
Schematic for photon migration through an objective. a Three-dimensional view; b two-dimensional view in the meridian plane. The full projection space for photons is illustrated in black, while the incident projection of a single photon is given in gray. The figure illustrates the case when n 1 > n 2
The x–y coordinate of the starting point A of the incident ray in the lens aperture is determined by a normalized two-dimensional circle random number generator which is scaled to the aperture diameter, D, of the lens [6]. The z-coordinate of the starting point A is given by the difference between the penetration depth , d′, and the focal length, f, of the lens, which is derived for a given lens of numerical aperture (NA) and aperture diameter, D 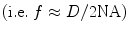 . It should be noted that the z-coordinate of point A is a constant less than 0, for a given lens, since all photon rays originate from the same x–y plane in the lens (see the shaded gray plane on the lens in Fig. 3.2). The ending point of the incident ray is given by point B, with its x–y–z coordinate defined as the geometric focus of the imaging lens (i.e., coordinates (0, 0, d′)).
. It should be noted that the z-coordinate of point A is a constant less than 0, for a given lens, since all photon rays originate from the same x–y plane in the lens (see the shaded gray plane on the lens in Fig. 3.2). The ending point of the incident ray is given by point B, with its x–y–z coordinate defined as the geometric focus of the imaging lens (i.e., coordinates (0, 0, d′)).
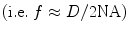 . It should be noted that the z-coordinate of point A is a constant less than 0, for a given lens, since all photon rays originate from the same x–y plane in the lens (see the shaded gray plane on the lens in Fig. 3.2). The ending point of the incident ray is given by point B, with its x–y–z coordinate defined as the geometric focus of the imaging lens (i.e., coordinates (0, 0, d′)).
. It should be noted that the z-coordinate of point A is a constant less than 0, for a given lens, since all photon rays originate from the same x–y plane in the lens (see the shaded gray plane on the lens in Fig. 3.2). The ending point of the incident ray is given by point B, with its x–y–z coordinate defined as the geometric focus of the imaging lens (i.e., coordinates (0, 0, d′)). Due to a change in the refractive index between the surrounding and turbid media, the focal plane defined by point B (see the dark gray plane in the turbid medium in Fig. 3.2) only represents the imaginary depth, d′, into the turbid medium. This means that the true focal plane, d, defined by point E, into the turbid sample must be determined with the aid of Snell’s law [4]:
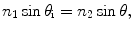
where n 1 and n 2 are the refractive indices of the surrounding and turbid media, respectively. θ i is the incident angle at which the ray of a projected photon, defined by points A and B, intersects with the turbid medium boundary at position C (see Fig. 3.2). It should be noted that in the Monte Carlo model spherical aberration is ignored. The convergent focal spot is determined from the maximum incident angle, θ i, i.e., the marginal ray of the imaging lens.
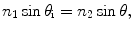
(3.5)
Reflection and transmission on the interface between a turbid medium and its surrounding medium (see point C in Fig. 3.2) are also considered in this simulation. A weighting factor, f p, is assigned to each photon to represent its contribution weighting. Initially the weighting factor, f p, is equal to 1. When a photon passes through a dielectric interface, the weighting of the photon in the transmitted (T) and reflected (R) directions are decided according to the Fresnel formulae [4]
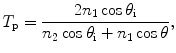
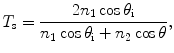
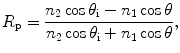
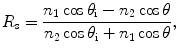
where the subscripts p and s represent parallel and perpendicular polarization components, respectively, while subscripts 1 and 2 represent the surrounding and turbid media, respectively.
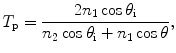
(3.6)
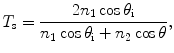
(3.7)
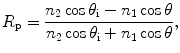
(3.8)
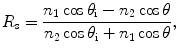
(3.9)
The initial values of the five parameters for a single photon (ray) incident to the turbid medium at point C are therefore obtained as follows: the spatial coordinates, x and y, and the angular coordinate, ϕ, are derived from the geometry in Fig. 3.2, while θ is obtained from Snell’s law (3.5). The spatial coordinate, z, is set to zero since all photons originate from the same boundary surface (z-plane) of the turbid medium. It should be noted that for transillumination modeling the values of z and θ are initially set to zero, since a parallel beam probe with respect to the turbid media is used.
Two typical scanning optical microscope arrangements used in Chaps. 5 and 6 can be simulated using the Monte Carlo model in Sect. 3.1. They are the transmission scanning optical microscope (Fig. 3.3a) and the reflection scanning optical microscope (Fig. 3.3b). For the transmission optical microscope illustrated in Fig. 3.3a, a parallel beam is incident upon the imaging lens L1, which has its focus on the embedded object. A separate collection lens L2 which has its focus overlapped with the imaging lens L1 is used to collect the light originating from a simulated turbid medium. The collection lens L2 is also used to focus the collected light onto the detector D. It should be noted that only the photons that fall within the collection cone of lens L2 will be traced to the detector plane by geometric optics . The simulated embedded object is placed at the center of the turbid medium in this optical arrangement. The simulated samples embedded within the turbid medium for the transmission arrangement are considered to have 100 % absorption. That is, when an incident photon hits the embedded object it ceases to be simulated. For the reflection microscope illustrated in Fig. 3.3b a parallel beam is incident upon the imaging lens L1 which has its focus on an embedded object. A collection lens L2 then focuses the collected light originating from the turbid medium onto the detector D. It should be noted that only the photons that fall within the collection cone of lens L2 are traced to the detector plane by geometric optics. In this arrangement the embedded object is placed on the back surface of the turbid medium. The simulated samples embedded within the turbid medium for the reflection arrangement are considered to have 100 % reflectivity. With this arrangement the reflection microscope is equivalent to folding the transmission microscope arrangement, at the embedded object, onto itself. It should be noted that the size of the detector used in the detection of the light originating from the simulated turbid media is determined by the effective size of the used pinhole , P (see Fig. 3.3).
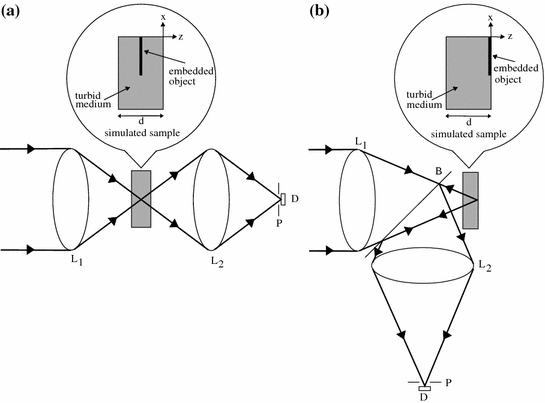

Fig. 3.3
Schematic diagram of the modeled transmission (a) and reflection (b) scanning optical microscopes. B beamsplitter; D detector; L lenses; P pinhole
3.3 Effect of Polarization
According to the Stokes vector theory in Sect. 2.3, once the scattering parameters, S 1(θ) and S 2(θ) in (2.24) and (2.25) are known, all elements of the scattering matrix, M, defined in (2.18) and (2.19), can be calculated. Thus the polarization gating mechanism that will be discussed in Chap. 6 can be modeled using the Monte Carlo simulation method.
Since calculating the scattering parameters, S 1(θ) and S 2(θ), is a time-consuming task, an approximation is used in the calculation of the scattering matrix , M, at each scattering event. Before simulation starts [7], the scattering angle, θ, between 0 and π is first divided into 1,000 equal intervals and the scattering parameters, S 1(θ) and S 2(θ), corresponding to those scattering angles are calculated. All the calculated scattering angles, θ, and the scattering parameters, S 1(θ) and S 2(θ), are stored in a database file. To employ polarization gating in the Monte Carlo simulation, Stokes parameters are defined for each incident photon in addition to the five existing parameters (x, y, z, θ and ϕ). At each scattering event in the Monte Carlo simulation [7] the scattering parameters, S 1(θ) and S 2(θ), are obtained by matching the scattering angle, θ s (determined by the Henyey–Greenstein probability distribution defined in (3.4)), with the closest scattering angle, θ, stored in the lookup database file. Then according to the chosen scattering angle, θ, and its corresponding scattering parameters, S 1(θ) and S 2(θ), all the elements of the scattering matrix, M, are calculated using (2.19)–(2.25). Therefore, a new Stokes vector can be calculated from (2.18).
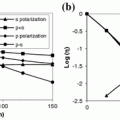
By monitoring the change of the polarization state of each photon at every scattering event, the depolarization of the light propagating through a turbid medium can be evaluated. The degree of polarization, γ, of the detected scattered light in this book is defined as
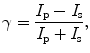
where I p and I s are the light intensity detected with the analyzer parallel and perpendicular to the incident polarization direction, respectively. Assuming that the incident light is linearly polarized in the x-direction, the parallel polarization intensity, I p, and the perpendicular polarization intensity, I s, can be calculated as
![$$I_{\text{p}} = I_{\text{scat}} \cdot \left[ {\begin{array}{*{20}c} 1 & 1 & 0 & 0 \\ \end{array} } \right],$$](/wp-content/uploads/2016/09/A71851_1_En_3_Chapter_Equ11.gif)
and
![$$I_{\text{s}} = I_{\text{scat}} \cdot \left[ {\begin{array}{*{20}c} 1 & { - 1} & 0 & 0 \\ \end{array} } \right].$$](/wp-content/uploads/2016/09/A71851_1_En_3_Chapter_Equ12.gif)
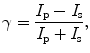
(3.10)
![$$I_{\text{p}} = I_{\text{scat}} \cdot \left[ {\begin{array}{*{20}c} 1 & 1 & 0 & 0 \\ \end{array} } \right],$$](/wp-content/uploads/2016/09/A71851_1_En_3_Chapter_Equ11.gif)
(3.11)
![$$I_{\text{s}} = I_{\text{scat}} \cdot \left[ {\begin{array}{*{20}c} 1 & { - 1} & 0 & 0 \\ \end{array} } \right].$$](/wp-content/uploads/2016/09/A71851_1_En_3_Chapter_Equ12.gif)
(3.12)
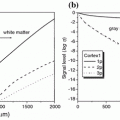
The polarization gating mechanisms used in Chap. 6 [7] are parallel (conventional) polarization-gating, based on the signal intensity (I p) detected with an analyzer parallel to the direction of the incident polarization, and perpendicular polarization-gating, based on the signal intensity (I s) detected with an analyzer perpendicular to the direction of the incident polarization. The third method of polarization-gating considered is differential polarization gating , which is based on the subtraction of the conventional polarization-gated intensity, I p, and the perpendicular polarization-gated intensity, I s [7].
3.4 Effect of Pulsed Illumination
To describe the pulse propagation through a turbid in the Monte Carlo model [3, 8], we need to include the difference of the photon propagation caused by time-of-flight in a pulsed beam. An ultrashort pulsed beam with pulse width, Δτ 0, has a finite distribution of wavelength (frequency) components. According to Mie scattering theory (see Sect. 2.2), the scattering coefficients , a i and b i , are related to the ratio between the radius of a scattering particle, a, and the wavelength of light, λ (see (2.1) to (2.4)). Therefore, for a given scattering particle radius, a, the scattering coefficients, a i and b i , for each wavelength component, λ, are different. Hence the scattering cross-section, σ s, and the anisotropy value, g, need to be determined for each individual wavelength component, λ, for an illumination pulse.
The effect of the broad spectrum of an ultrashort pulse on the scattering efficiency, Q s, and the anisotropy value, g, becomes more pronounced as the pulse width, Δτ 0, becomes shorter. Let us consider that the intensity of an illumination source is a Gaussian-shaped pulse given as [9]
![$$U_{0} (t) = \exp ( - i\omega_{0} t)\exp \left[ { - \left( \frac{t}{T} \right)^{2} } \right],$$](/wp-content/uploads/2016/09/A71851_1_En_3_Chapter_Equ13.gif)
where t is the local time coordinate, T is related to the pulse width ∆τ 0 via 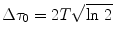 , and ω 0 is the central frequency. The corresponding Fourier spectrum for the Gaussian-shaped pulse is then given as [9]
, and ω 0 is the central frequency. The corresponding Fourier spectrum for the Gaussian-shaped pulse is then given as [9]
![$$V_{0} (\Delta \varOmega ) = \sqrt \pi T\exp \left[ { - \left( {\frac{T\Delta \varOmega }{2}} \right)^{2} } \right],$$](/wp-content/uploads/2016/09/A71851_1_En_3_Chapter_Equ14.gif)
where ∆Ω is the spectral width which is defined as the total bandwidth between two positions at which the intensity drops to one half of its peak value. The relationship between the pulse width ∆τ 0, and the spectral width ∆Ω for the pulse is then given as [8]
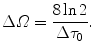
For example, a 10-fs pulse with a central wavelength, λ 0 of 700 nm, has a corresponding spectral width, ∆Ω, of approximately 0.206. Note that in this case the spectral width, ∆Ω, is normalized by the central frequency, ω 0 (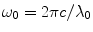 , where c = 3 × 108 m/s).
, where c = 3 × 108 m/s).
![$$U_{0} (t) = \exp ( - i\omega_{0} t)\exp \left[ { - \left( \frac{t}{T} \right)^{2} } \right],$$](/wp-content/uploads/2016/09/A71851_1_En_3_Chapter_Equ13.gif)
(3.13)
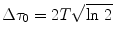 , and ω 0 is the central frequency. The corresponding Fourier spectrum for the Gaussian-shaped pulse is then given as [9]
, and ω 0 is the central frequency. The corresponding Fourier spectrum for the Gaussian-shaped pulse is then given as [9]![$$V_{0} (\Delta \varOmega ) = \sqrt \pi T\exp \left[ { - \left( {\frac{T\Delta \varOmega }{2}} \right)^{2} } \right],$$](/wp-content/uploads/2016/09/A71851_1_En_3_Chapter_Equ14.gif)
(3.14)
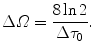
(3.15)
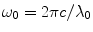 , where c = 3 × 108 m/s).
, where c = 3 × 108 m/s).To understand the effect of the spectral width, ∆Ω, on the scattering efficiency , Q s, and the anisotropy value, g, we define two parameters,
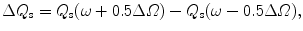
and
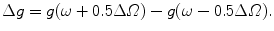
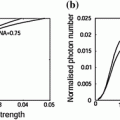
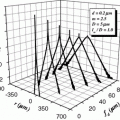
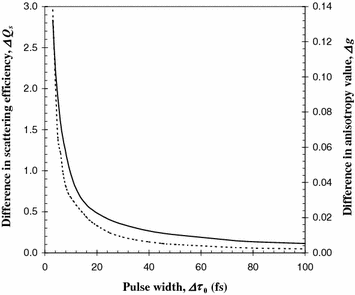
Since the pulse width, ∆τ 0, can be directly related to the frequency bandwidth , ∆Ω we can plot the difference in the scattering efficiency, ∆Q s and the difference in the anisotropy value, ∆g, as a function of the pulse width ∆τ 0. Figure 3.4 is the effect of the pulse width, ∆τ 0, on the difference in the scattering efficiency, ∆Q s and the difference in anisotropy value, ∆g, for a central wavelength, λ 0, of 700 nm and a scattering particle radius, a, of 0.518 μm [3]. It is seen that the difference in the scattering efficiency, ∆Q s, and the difference in the anisotropy value , ∆g, both increase as the pulse width, ∆t 0, decreases. For the pulse width, ∆τ 0, less than 20 fs the difference in the scattering efficiency, ∆Q s, and the difference in the anisotropy value, ∆g, become more pronounced, indicating that the effect of the frequency bandwidth is more significant in this region.
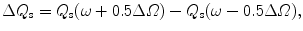
(3.16)
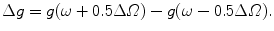
(3.17)

Fig. 3.4
Difference in the scattering efficiency, ΔQ s, (solid curve) and the difference in the anisotropy value, Δg, (dashed curve) as a function of the pulse width, Δτ 0 (n 1 = 1.33 and n 2 = 1.59)
With the help of Fig. 3.4, the illumination of an ultrashort pulse can be incorporated into the Monte Carlo simulation by describing that the temporal distribution of incident photons is given by the following Gaussian profile [3]:
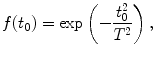
where t 0 is the departure time of a photon. The departure time, t 0, of photons in the pulse is randomly chosen according to the temporal distribution in (3.18).
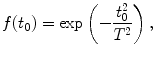
(3.18)
3.5 Photon Migration Through a Layer of a Turbid Medium
In the case of Monte Carlo simulation of photon propagation through a layer of a scattering medium, photons are simply treated as particles without any wave feature. Individual photons suffer events of scattering and absorption, which is related to the local optical properties of the turbid medium characterized by scattering coefficient μ s and absorption coefficient μ a (Fig. 3.5). This 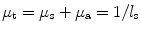 . The Monte Carlo simulation is performed by a numerical step-by-step tracing of the random migration of the photons within the scattering medium until their annihilation or escapement [10, 11].
. The Monte Carlo simulation is performed by a numerical step-by-step tracing of the random migration of the photons within the scattering medium until their annihilation or escapement [10, 11].
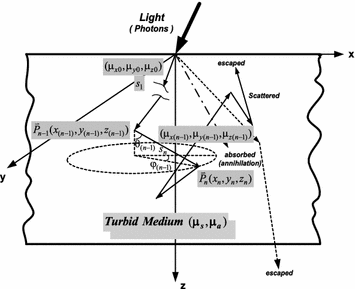
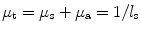 . The Monte Carlo simulation is performed by a numerical step-by-step tracing of the random migration of the photons within the scattering medium until their annihilation or escapement [10, 11].
. The Monte Carlo simulation is performed by a numerical step-by-step tracing of the random migration of the photons within the scattering medium until their annihilation or escapement [10, 11].
Fig. 3.5
Schematic diagram of the Monte Carlo simulation in dealing with the photon propagation through a later of s scattering medium
It is clear that each step a photon may take from the position 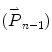 to the next position
to the next position 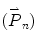 can be easily traced by three random variables in a three-dimensional dynamic spherical coordinate system according to Fig. 3.5, they are the step length (s), the deflection angle (0 ≤ θ < π), and the azimuthal angle (0 < φ < 2π), which, respectively, describe the distance a photon takes between two successive photon–medium interaction sites, the angle of deflection between the photon propagation direction from the z axis and the corresponding azimuthal angle when a scattering event occurs.
can be easily traced by three random variables in a three-dimensional dynamic spherical coordinate system according to Fig. 3.5, they are the step length (s), the deflection angle (0 ≤ θ < π), and the azimuthal angle (0 < φ < 2π), which, respectively, describe the distance a photon takes between two successive photon–medium interaction sites, the angle of deflection between the photon propagation direction from the z axis and the corresponding azimuthal angle when a scattering event occurs.
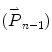 to the next position
to the next position 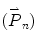 can be easily traced by three random variables in a three-dimensional dynamic spherical coordinate system according to Fig. 3.5, they are the step length (s), the deflection angle (0 ≤ θ < π), and the azimuthal angle (0 < φ < 2π), which, respectively, describe the distance a photon takes between two successive photon–medium interaction sites, the angle of deflection between the photon propagation direction from the z axis and the corresponding azimuthal angle when a scattering event occurs.
can be easily traced by three random variables in a three-dimensional dynamic spherical coordinate system according to Fig. 3.5, they are the step length (s), the deflection angle (0 ≤ θ < π), and the azimuthal angle (0 < φ < 2π), which, respectively, describe the distance a photon takes between two successive photon–medium interaction sites, the angle of deflection between the photon propagation direction from the z axis and the corresponding azimuthal angle when a scattering event occurs.The value distributions of the variables such as the step length (s) and the scattering angles (θ, φ) are determined by their corresponding physically described probability density functions p(s), p(θ), p(φ), based on the following sampling rules:
![$$\left\{ {\begin{array}{*{20}l} {\int\limits_{a}^{b} {p(x) = 1} } \hfill & {\text{for}} \hfill & {x \in [a,b]} \hfill \\ {\int\limits_{a}^{{x_{1} }} {p(x) = \xi_{1} } } \hfill & {\text{for}} \hfill & {\xi_{1} \in [0,1]} \hfill \\ \end{array} } \right.$$](/wp-content/uploads/2016/09/A71851_1_En_3_Chapter_Equ19.gif)
where x represents any of the random variables s, θ, or φ and ξ 1 are one of the uniformly distributed random numbers within 0–1.
![$$\left\{ {\begin{array}{*{20}l} {\int\limits_{a}^{b} {p(x) = 1} } \hfill & {\text{for}} \hfill & {x \in [a,b]} \hfill \\ {\int\limits_{a}^{{x_{1} }} {p(x) = \xi_{1} } } \hfill & {\text{for}} \hfill & {\xi_{1} \in [0,1]} \hfill \\ \end{array} } \right.$$](/wp-content/uploads/2016/09/A71851_1_En_3_Chapter_Equ19.gif)
(3.19)
The probability function p(s) can be derived Beer’s law and the Henyey and Greenstein function , as shown in Sect. 3.1. Therefore, the choice for s, cos θ and φ can be expressed as