MRI scans 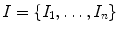 where each 3D MRI scan
where each 3D MRI scan 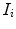 has a corresponding real number clinical score
has a corresponding real number clinical score 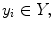 and a corresponding spinal cord segmentation
and a corresponding spinal cord segmentation 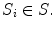 The dimensions of
The dimensions of 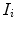 and
and 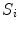 are the same. Each voxel in
are the same. Each voxel in 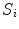 has a value between 0 and 1, where 0 represents the background and 1 represents the spinal cord. Voxels in
has a value between 0 and 1, where 0 represents the background and 1 represents the spinal cord. Voxels in 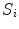 that are on the boundary of the spinal cord are assigned a fuzzy value between 0 and 1 that represents an estimated percentage of the voxel that contains spinal cord (i.e., partial volume) [15].
that are on the boundary of the spinal cord are assigned a fuzzy value between 0 and 1 that represents an estimated percentage of the voxel that contains spinal cord (i.e., partial volume) [15].
Our objective is to create a model 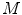 , using the images
, using the images 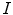 and segmentations
and segmentations 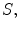 capable of predicting the patients’ clinical scores
capable of predicting the patients’ clinical scores 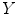 from novel MR images. We extract a set of features
from novel MR images. We extract a set of features 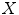 from
from 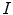 and
and 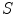 that are transformed by model
that are transformed by model 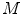 into values
into values 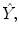 such that these predicted values
such that these predicted values 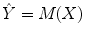 estimate the corresponding clinical scores
estimate the corresponding clinical scores 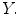
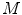 , using the images
, using the images 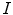 and segmentations
and segmentations 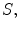 capable of predicting the patients’ clinical scores
capable of predicting the patients’ clinical scores 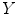 from novel MR images. We extract a set of features
from novel MR images. We extract a set of features 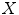 from
from 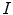 and
and 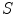 that are transformed by model
that are transformed by model 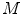 into values
into values 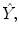 such that these predicted values
such that these predicted values 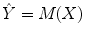 estimate the corresponding clinical scores
estimate the corresponding clinical scores 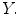
One approach is to set 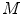 as a simple linear regression model with the spinal cord volume as the single explanatory variable
as a simple linear regression model with the spinal cord volume as the single explanatory variable 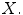 This is similar to the existing literature where a Pearson’s correlation coefficient is computed to measure the linear dependency between the spinal cord volume and clinical score. However, as mentioned in the introduction, this linear dependency using spinal cord volume does not always reveal a strong clinical relationship. We improve on this by deriving new morphological and MRI-based appearance features
This is similar to the existing literature where a Pearson’s correlation coefficient is computed to measure the linear dependency between the spinal cord volume and clinical score. However, as mentioned in the introduction, this linear dependency using spinal cord volume does not always reveal a strong clinical relationship. We improve on this by deriving new morphological and MRI-based appearance features 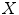 and examining ways to combine them in more descriptive models
and examining ways to combine them in more descriptive models 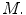
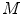 as a simple linear regression model with the spinal cord volume as the single explanatory variable
as a simple linear regression model with the spinal cord volume as the single explanatory variable 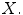 This is similar to the existing literature where a Pearson’s correlation coefficient is computed to measure the linear dependency between the spinal cord volume and clinical score. However, as mentioned in the introduction, this linear dependency using spinal cord volume does not always reveal a strong clinical relationship. We improve on this by deriving new morphological and MRI-based appearance features
This is similar to the existing literature where a Pearson’s correlation coefficient is computed to measure the linear dependency between the spinal cord volume and clinical score. However, as mentioned in the introduction, this linear dependency using spinal cord volume does not always reveal a strong clinical relationship. We improve on this by deriving new morphological and MRI-based appearance features 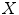 and examining ways to combine them in more descriptive models
and examining ways to combine them in more descriptive models 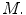
2.2 Candidate Features
We describe simple candidate morphological and appearance features 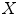 that are potentially sensitive to spinal cord changes. This is not meant to be a comprehensive set of features, but is sufficient to explore the potential of going beyond measuring cord size to predict disability. We first define the commonly used spinal cord volume, which is computed by summing all voxels, including the partial volumes
that are potentially sensitive to spinal cord changes. This is not meant to be a comprehensive set of features, but is sufficient to explore the potential of going beyond measuring cord size to predict disability. We first define the commonly used spinal cord volume, which is computed by summing all voxels, including the partial volumes ![$$S_i(j)\in [0,1],$$](/wp-content/uploads/2016/03/A323246_1_En_6_Chapter_IEq26.gif) in the segmentation,
in the segmentation, 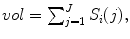 where
where 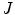 is the total number of voxels in
is the total number of voxels in 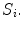 While spinal cord volume captures a global measure of spinal cord atrophy, we are also interested in features that vary at least partly independently from area or volume, and that are sensitive to spinal cord changes at a local scale.
While spinal cord volume captures a global measure of spinal cord atrophy, we are also interested in features that vary at least partly independently from area or volume, and that are sensitive to spinal cord changes at a local scale.
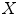 that are potentially sensitive to spinal cord changes. This is not meant to be a comprehensive set of features, but is sufficient to explore the potential of going beyond measuring cord size to predict disability. We first define the commonly used spinal cord volume, which is computed by summing all voxels, including the partial volumes
that are potentially sensitive to spinal cord changes. This is not meant to be a comprehensive set of features, but is sufficient to explore the potential of going beyond measuring cord size to predict disability. We first define the commonly used spinal cord volume, which is computed by summing all voxels, including the partial volumes ![$$S_i(j)\in [0,1],$$](/wp-content/uploads/2016/03/A323246_1_En_6_Chapter_IEq26.gif) in the segmentation,
in the segmentation, 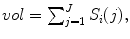 where
where 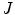 is the total number of voxels in
is the total number of voxels in 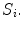 While spinal cord volume captures a global measure of spinal cord atrophy, we are also interested in features that vary at least partly independently from area or volume, and that are sensitive to spinal cord changes at a local scale.
While spinal cord volume captures a global measure of spinal cord atrophy, we are also interested in features that vary at least partly independently from area or volume, and that are sensitive to spinal cord changes at a local scale.
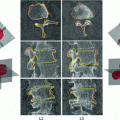
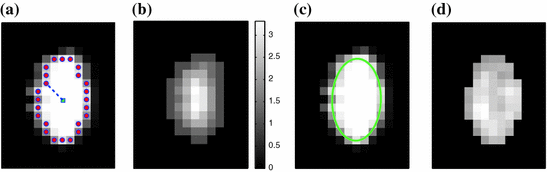
Fig. 1
Illustrations of the proposed features. a The distances (dashed line) from the center-of-mass (center box) to the boundary voxels (circles) make up 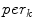 . b The distances to the nearest boundary point from the voxels inside the cord give
. b The distances to the nearest boundary point from the voxels inside the cord give 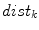 (brighter implies farther). c An ellipse is fit to the cord. d The normalized intensities of the cord are considered in
(brighter implies farther). c An ellipse is fit to the cord. d The normalized intensities of the cord are considered in 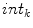
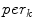 . b The distances to the nearest boundary point from the voxels inside the cord give
. b The distances to the nearest boundary point from the voxels inside the cord give 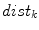 (brighter implies farther). c An ellipse is fit to the cord. d The normalized intensities of the cord are considered in
(brighter implies farther). c An ellipse is fit to the cord. d The normalized intensities of the cord are considered in 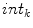
Our first proposed feature is designed to be more sensitive to local changes in the spinal cord’s boundary. On each 2D axial slice of the segmentation 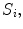 we find voxels on the boundary between the spinal cord and background by considering voxels in
we find voxels on the boundary between the spinal cord and background by considering voxels in 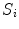 with a partial volume greater than 0.5 to be spinal cord. This results in a 2D binary image that we use to extract the cord’s boundary voxels. For the
with a partial volume greater than 0.5 to be spinal cord. This results in a 2D binary image that we use to extract the cord’s boundary voxels. For the 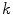 th 2D axial slice of the spinal cord, we take the Euclidean distance between the center-of-mass
th 2D axial slice of the spinal cord, we take the Euclidean distance between the center-of-mass 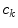 of the cord’s
of the cord’s 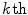 cross section, and the spinal cord boundary/perimeter voxels
cross section, and the spinal cord boundary/perimeter voxels 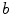 computed as,
computed as, 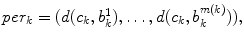 where
where 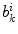 represents the
represents the 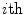 boundary voxel on the
boundary voxel on the 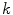 th slice, and
th slice, and 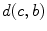 computes the Euclidean distance between the two coordinates (Fig. 1a). The number of boundary voxels
computes the Euclidean distance between the two coordinates (Fig. 1a). The number of boundary voxels 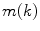 can change for each 2D slice. We find the minimum distance from the center-of-mass to the boundary voxels in each 2D slice averaged over
can change for each 2D slice. We find the minimum distance from the center-of-mass to the boundary voxels in each 2D slice averaged over 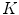 2D slices,
2D slices,
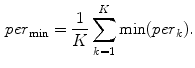
In a similar way, to compute additional features we replace the “min” function from (1) with the mean (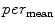 ), standard deviation (
), standard deviation (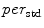 ), and the max (
), and the max (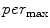 ) functions.
) functions.
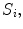 we find voxels on the boundary between the spinal cord and background by considering voxels in
we find voxels on the boundary between the spinal cord and background by considering voxels in 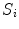 with a partial volume greater than 0.5 to be spinal cord. This results in a 2D binary image that we use to extract the cord’s boundary voxels. For the
with a partial volume greater than 0.5 to be spinal cord. This results in a 2D binary image that we use to extract the cord’s boundary voxels. For the 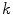 th 2D axial slice of the spinal cord, we take the Euclidean distance between the center-of-mass
th 2D axial slice of the spinal cord, we take the Euclidean distance between the center-of-mass 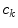 of the cord’s
of the cord’s 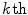 cross section, and the spinal cord boundary/perimeter voxels
cross section, and the spinal cord boundary/perimeter voxels 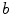 computed as,
computed as, 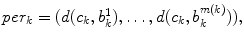 where
where 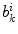 represents the
represents the 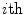 boundary voxel on the
boundary voxel on the 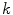 th slice, and
th slice, and 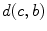 computes the Euclidean distance between the two coordinates (Fig. 1a). The number of boundary voxels
computes the Euclidean distance between the two coordinates (Fig. 1a). The number of boundary voxels 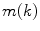 can change for each 2D slice. We find the minimum distance from the center-of-mass to the boundary voxels in each 2D slice averaged over
can change for each 2D slice. We find the minimum distance from the center-of-mass to the boundary voxels in each 2D slice averaged over 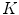 2D slices,
2D slices,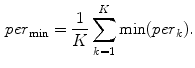
(1)
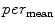 ), standard deviation (
), standard deviation (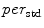 ), and the max (
), and the max (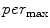 ) functions.
) functions.We define a related measure that focuses on local changes in 3D by calculating a 3D distance transform from the surface of the segmented spinal cord masked by (or restricted to) the interior region of the cord. To compute the distance transform, we calculate the Euclidean distance between voxels inside the spinal cord and the nearest boundary voxel in 3D. To further differentiate this feature from the 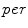 features, we consider voxels that contain any partial volume to be spinal cord, which changes the boundary voxels. The distance transform for slice
features, we consider voxels that contain any partial volume to be spinal cord, which changes the boundary voxels. The distance transform for slice 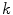 with
with 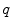 voxels inside the cord is represented as
voxels inside the cord is represented as 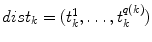 where
where 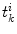 is the distance from the
is the distance from the 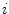 th voxel inside the cord on the
th voxel inside the cord on the 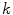 th slice to the nearest 3D boundary coordinate (Fig. 1b). The number of voxels inside the cord,
th slice to the nearest 3D boundary coordinate (Fig. 1b). The number of voxels inside the cord, 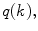 can change for each 2D slice. In a similar fashion to (1), we replace
can change for each 2D slice. In a similar fashion to (1), we replace 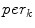 with
with 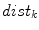 and the “min” function with the mean (
and the “min” function with the mean ( ), max (
), max (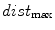 ), standard deviation (
), standard deviation (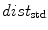 ) and the max divided by the mean distance (
) and the max divided by the mean distance (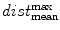 ) function averaged over the
) function averaged over the 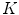 2D slices. For clarity we formally define,
2D slices. For clarity we formally define,
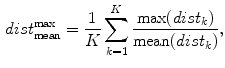
which averages the ratio of the furthest boundary distance by the mean distance.
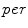 features, we consider voxels that contain any partial volume to be spinal cord, which changes the boundary voxels. The distance transform for slice
features, we consider voxels that contain any partial volume to be spinal cord, which changes the boundary voxels. The distance transform for slice 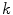 with
with 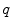 voxels inside the cord is represented as
voxels inside the cord is represented as 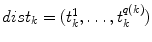 where
where 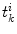 is the distance from the
is the distance from the 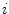 th voxel inside the cord on the
th voxel inside the cord on the 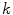 th slice to the nearest 3D boundary coordinate (Fig. 1b). The number of voxels inside the cord,
th slice to the nearest 3D boundary coordinate (Fig. 1b). The number of voxels inside the cord, 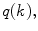 can change for each 2D slice. In a similar fashion to (1), we replace
can change for each 2D slice. In a similar fashion to (1), we replace 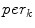 with
with 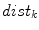 and the “min” function with the mean (
and the “min” function with the mean ( ), max (
), max (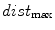 ), standard deviation (
), standard deviation (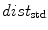 ) and the max divided by the mean distance (
) and the max divided by the mean distance (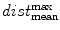 ) function averaged over the
) function averaged over the 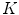 2D slices. For clarity we formally define,
2D slices. For clarity we formally define,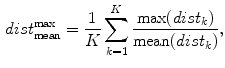
(2)
To compute features that are more robust to local noise, such as small segmentation errors, we fit an ellipse (Fig. 1c) to each 2D cross-sectional slice of the segmented spinal cord and compute the eccentricity (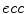 ), minor axis (
), minor axis (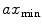 ), and major axis (
), and major axis (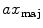 ), averaged over the length the cord.
), averaged over the length the cord.
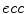 ), minor axis (
), minor axis (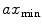 ), and major axis (
), and major axis (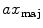 ), averaged over the length the cord.
), averaged over the length the cord.All the features proposed so far are dependent on the geometrical characteristics of the cord, but we also include features based on the intensities found within the MRI. As the intensity values can vary widely in different MRI scans, we normalize a scan’s intensities by its overall 3D scan intensities to produce z-scores. We extract the z-scores of those voxels that are labelled as spinal cord (partial volume 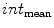 ) and standard deviation (
) and standard deviation (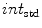 ) of the spinal cord intensity values averaged over the
) of the spinal cord intensity values averaged over the 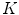 2D slices (Fig. 1d).
2D slices (Fig. 1d).
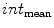 ) and standard deviation (
) and standard deviation (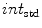 ) of the spinal cord intensity values averaged over the
) of the spinal cord intensity values averaged over the 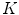 2D slices (Fig. 1d).
2D slices (Fig. 1d).2.3 Regression Models
Linear regression employs a linear function to model the relationship between the explanatory variable (e.g. spinal cord volume) and a response variable (clinical score). The parameters of this model are the coefficients 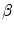 of the explanatory variables and the error term
of the explanatory variables and the error term 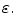 These coefficients can be estimated from the data by applying a least-squares fitting that minimizes the differences between the response variable and the fitted explanatory variable. A model with only a single explanatory variable
These coefficients can be estimated from the data by applying a least-squares fitting that minimizes the differences between the response variable and the fitted explanatory variable. A model with only a single explanatory variable 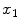 , is known as simple linear regression, and is one of the simplest models to analyze. Given a dataset with
, is known as simple linear regression, and is one of the simplest models to analyze. Given a dataset with 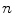 observations, this produces a straight line,
observations, this produces a straight line, 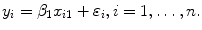 Multiple linear regression builds on this by adding
Multiple linear regression builds on this by adding 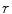 explanatory variables to the model,
explanatory variables to the model, 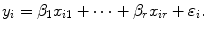
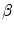 of the explanatory variables and the error term
of the explanatory variables and the error term 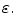 These coefficients can be estimated from the data by applying a least-squares fitting that minimizes the differences between the response variable and the fitted explanatory variable. A model with only a single explanatory variable
These coefficients can be estimated from the data by applying a least-squares fitting that minimizes the differences between the response variable and the fitted explanatory variable. A model with only a single explanatory variable 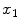 , is known as simple linear regression, and is one of the simplest models to analyze. Given a dataset with
, is known as simple linear regression, and is one of the simplest models to analyze. Given a dataset with 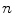 observations, this produces a straight line,
observations, this produces a straight line, 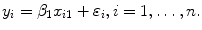 Multiple linear regression builds on this by adding
Multiple linear regression builds on this by adding 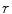 explanatory variables to the model,
explanatory variables to the model, 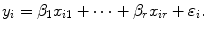
While these models assume a linearity of the underlying relations, we also explore a more flexible, non-linear, non-parametric model, known as a regression forest. A regression forest significantly differs from the previously described models as it is completely learned from the data and makes no assumptions about the underlying distributions [2].
2.4 Training and Testing the Models
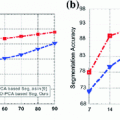
The models in Sect. 2.3, are described in order of increasing complexity. With this added complexity, we increase the potential to accurately model the underlying function, but also increase the difficulty in intuitively understanding the model and increase the likelihood of over-fitting the model to the training data. To reduce the possibility of over-fitting, we divide our data into a training and testing set. Given the relatively small size of our dataset, we use leave-one-out cross-validation. This is repeated for all samples to give us an indication of the robustness and generalizability of our regression model and chosen features.
2.5 Clinical Scores
As discussed in the introduction, the EDSS and the MSFC scores, which we aim to predict from 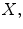 are commonly used to quantify clinical disability. We choose to focus on the MSFC score rather than the EDSS score because the MSFC captures disability to which the EDSS score is relatively insensitive, such as arm/hand function. In addition, the EDSS scores tend to exhibit a poor distribution due to the non-linearity of the scale, with many patients clustered between 4.5 and 6.5 (Fig. 2a).
are commonly used to quantify clinical disability. We choose to focus on the MSFC score rather than the EDSS score because the MSFC captures disability to which the EDSS score is relatively insensitive, such as arm/hand function. In addition, the EDSS scores tend to exhibit a poor distribution due to the non-linearity of the scale, with many patients clustered between 4.5 and 6.5 (Fig. 2a).
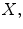 are commonly used to quantify clinical disability. We choose to focus on the MSFC score rather than the EDSS score because the MSFC captures disability to which the EDSS score is relatively insensitive, such as arm/hand function. In addition, the EDSS scores tend to exhibit a poor distribution due to the non-linearity of the scale, with many patients clustered between 4.5 and 6.5 (Fig. 2a).
are commonly used to quantify clinical disability. We choose to focus on the MSFC score rather than the EDSS score because the MSFC captures disability to which the EDSS score is relatively insensitive, such as arm/hand function. In addition, the EDSS scores tend to exhibit a poor distribution due to the non-linearity of the scale, with many patients clustered between 4.5 and 6.5 (Fig. 2a).The MSFC score tests for: upper extremity function, determined by a 9-hole peg test (9-HPT); walking speed, measured by a timed 25-foot walk (T25W); and cognitive function, evaluated by a paced auditory serial addition test (PASAT). These three tests are shown to vary relatively independently, be sensitive to changes over time, and capture aspects of MS that are not captured in the EDSS score [3




Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree