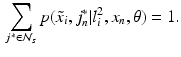given an observed image 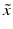 from a different imaging modality and a database of N previously observed image pairs
from a different imaging modality and a database of N previously observed image pairs 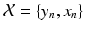 , indexed by n. Note that the technique can be easily extended to more than 2 modalities. The process of collapsing all the available information from
, indexed by n. Note that the technique can be easily extended to more than 2 modalities. The process of collapsing all the available information from 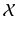 into one single estimate
into one single estimate ![$$E[\tilde{y}]$$](/wp-content/uploads/2016/09/A339424_1_En_2_Chapter_IEq5.gif) ignores both the fact that generating
ignores both the fact that generating 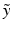 is an uncertain process an that
is an uncertain process an that 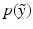 can be multimodal. Thus, contrary to [2, 4], where only the expected image
can be multimodal. Thus, contrary to [2, 4], where only the expected image ![$$E[\tilde{y}]$$](/wp-content/uploads/2016/09/A339424_1_En_2_Chapter_IEq8.gif) is generated, we characterise
is generated, we characterise 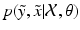 , i.e. the joint probability of observing the image pair
, i.e. the joint probability of observing the image pair 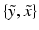 given a set of N previously observed templates
given a set of N previously observed templates 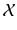 and the model parameters
and the model parameters 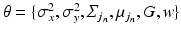 .
.
From an intuitive point of view, the main difference between the proposed method and previous approaches pertains with the idea that the process of image synthesis is uncertain. Thus, rather than trying to find the expected observation y from an observation x, we estimate what is the probability of observing different values of y when observing x.
2.1 The Observation Model
In order to estimate 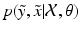 one has to first note that, due to the presence of pathology or imaging artefacts, not all intensity pairs
one has to first note that, due to the presence of pathology or imaging artefacts, not all intensity pairs 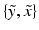 will be likely given a certain set of previously observed images. Thus, it is important to model the possible presence of outliers – intensity pairs that deviate from previous templates. This does not mean that one would be able to predict unseen pathological intensity pairs. Instead, the model assumes that imaging data can fall outside the predictable intensity patterns.
will be likely given a certain set of previously observed images. Thus, it is important to model the possible presence of outliers – intensity pairs that deviate from previous templates. This does not mean that one would be able to predict unseen pathological intensity pairs. Instead, the model assumes that imaging data can fall outside the predictable intensity patterns.
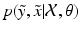 one has to first note that, due to the presence of pathology or imaging artefacts, not all intensity pairs
one has to first note that, due to the presence of pathology or imaging artefacts, not all intensity pairs 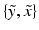 will be likely given a certain set of previously observed images. Thus, it is important to model the possible presence of outliers – intensity pairs that deviate from previous templates. This does not mean that one would be able to predict unseen pathological intensity pairs. Instead, the model assumes that imaging data can fall outside the predictable intensity patterns.
will be likely given a certain set of previously observed images. Thus, it is important to model the possible presence of outliers – intensity pairs that deviate from previous templates. This does not mean that one would be able to predict unseen pathological intensity pairs. Instead, the model assumes that imaging data can fall outside the predictable intensity patterns.With this aim in mind, the proposed generative model assumes that the observed data is generated from a mixture of 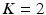 classes labeled by
classes labeled by 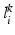 , i.e. an inlier class, derived from previous observations, and an outlier class, modelled by a uniform distribution. The probability
, i.e. an inlier class, derived from previous observations, and an outlier class, modelled by a uniform distribution. The probability 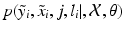 of observing an intensity pair
of observing an intensity pair 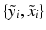 , a transformation j and label l at location i, is then defined as
, a transformation j and label l at location i, is then defined as
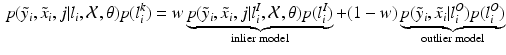 In this model, the distribution of the pair
In this model, the distribution of the pair 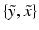 for the outlier class (
for the outlier class (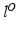 ) is given by an uniform distribution
) is given by an uniform distribution 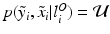 , an inlier class (
, an inlier class (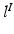 ) describing the similarity between the observed pair
) describing the similarity between the observed pair 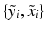 and the previously observed pairs
and the previously observed pairs 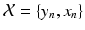 , a coordinate mapping
, a coordinate mapping 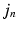 , a prior distribution
, a prior distribution 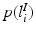 and
and 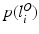 over the labelling
over the labelling 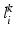 , and a global mixing weight w.
, and a global mixing weight w.
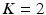 classes labeled by
classes labeled by 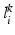 , i.e. an inlier class, derived from previous observations, and an outlier class, modelled by a uniform distribution. The probability
, i.e. an inlier class, derived from previous observations, and an outlier class, modelled by a uniform distribution. The probability 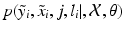 of observing an intensity pair
of observing an intensity pair 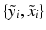 , a transformation j and label l at location i, is then defined as
, a transformation j and label l at location i, is then defined as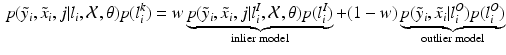
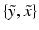 for the outlier class (
for the outlier class (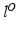 ) is given by an uniform distribution
) is given by an uniform distribution 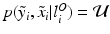 , an inlier class (
, an inlier class (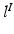 ) describing the similarity between the observed pair
) describing the similarity between the observed pair 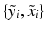 and the previously observed pairs
and the previously observed pairs 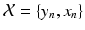 , a coordinate mapping
, a coordinate mapping 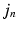 , a prior distribution
, a prior distribution 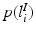 and
and 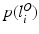 over the labelling
over the labelling 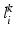 , and a global mixing weight w.
, and a global mixing weight w.In this work, given N previously observed images, the inlier model is defined as a mixture model given by
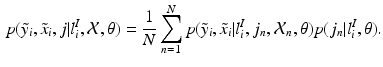 i.e., the probability of observing a certain pair of intensities
i.e., the probability of observing a certain pair of intensities 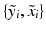 is a equally-weighted mixture of the N probabilities of observing the pair given a previously observed pair
is a equally-weighted mixture of the N probabilities of observing the pair given a previously observed pair 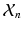 .
.
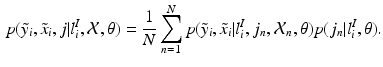
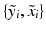 is a equally-weighted mixture of the N probabilities of observing the pair given a previously observed pair
is a equally-weighted mixture of the N probabilities of observing the pair given a previously observed pair 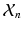 .
.As in the Non-Local STAPLE algorithm [6], we assume that 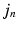 is unknown, or at least uncertain, as the coordinate mapping problem is ill posed [7]. As in Simpson et al. [7],
is unknown, or at least uncertain, as the coordinate mapping problem is ill posed [7]. As in Simpson et al. [7], 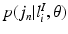 is a multivariate Gaussian distribution with parameters
is a multivariate Gaussian distribution with parameters 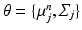 . Here, the expectation of the mapping
. Here, the expectation of the mapping 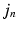 , i.e.
, i.e. 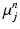 , is estimated using a multimodal pairwise b-spline parameterised registration between the observed image pair and the n-th image pair. A multichannel locally normalised cross correlation is used as an image similarity for registration purposes. In addition, the precision matrix
, is estimated using a multimodal pairwise b-spline parameterised registration between the observed image pair and the n-th image pair. A multichannel locally normalised cross correlation is used as an image similarity for registration purposes. In addition, the precision matrix 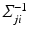 at location i, represents the inverse of the local directional estimate of registration uncertainty as described in [7]. In this work,
at location i, represents the inverse of the local directional estimate of registration uncertainty as described in [7]. In this work, 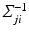 is approximated using the local second-moment matrix, also known as the structure tensor [8], of the observed image
is approximated using the local second-moment matrix, also known as the structure tensor [8], of the observed image 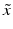 in a cubic convolution region of size
in a cubic convolution region of size 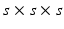 (empirically set to
(empirically set to 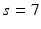 voxels). This covariance uncertainty approximation assumes that the registration in more uncertain along the edges of the image than across them. Thus,
voxels). This covariance uncertainty approximation assumes that the registration in more uncertain along the edges of the image than across them. Thus, 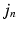 is less likely if it deviates from
is less likely if it deviates from 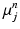 in a direction orthogonal to the image edges. In future work, this approximation will be replaced by a local covariance estimate as provided by Simpson et al. [7].
in a direction orthogonal to the image edges. In future work, this approximation will be replaced by a local covariance estimate as provided by Simpson et al. [7].
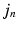 is unknown, or at least uncertain, as the coordinate mapping problem is ill posed [7]. As in Simpson et al. [7],
is unknown, or at least uncertain, as the coordinate mapping problem is ill posed [7]. As in Simpson et al. [7], 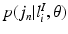 is a multivariate Gaussian distribution with parameters
is a multivariate Gaussian distribution with parameters 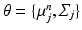 . Here, the expectation of the mapping
. Here, the expectation of the mapping 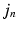 , i.e.
, i.e. 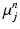 , is estimated using a multimodal pairwise b-spline parameterised registration between the observed image pair and the n-th image pair. A multichannel locally normalised cross correlation is used as an image similarity for registration purposes. In addition, the precision matrix
, is estimated using a multimodal pairwise b-spline parameterised registration between the observed image pair and the n-th image pair. A multichannel locally normalised cross correlation is used as an image similarity for registration purposes. In addition, the precision matrix 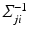 at location i, represents the inverse of the local directional estimate of registration uncertainty as described in [7]. In this work,
at location i, represents the inverse of the local directional estimate of registration uncertainty as described in [7]. In this work, 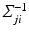 is approximated using the local second-moment matrix, also known as the structure tensor [8], of the observed image
is approximated using the local second-moment matrix, also known as the structure tensor [8], of the observed image 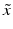 in a cubic convolution region of size
in a cubic convolution region of size 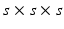 (empirically set to
(empirically set to 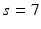 voxels). This covariance uncertainty approximation assumes that the registration in more uncertain along the edges of the image than across them. Thus,
voxels). This covariance uncertainty approximation assumes that the registration in more uncertain along the edges of the image than across them. Thus, 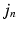 is less likely if it deviates from
is less likely if it deviates from 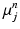 in a direction orthogonal to the image edges. In future work, this approximation will be replaced by a local covariance estimate as provided by Simpson et al. [7].
in a direction orthogonal to the image edges. In future work, this approximation will be replaced by a local covariance estimate as provided by Simpson et al. [7].Similarly to [6], as 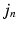 is unknown,
is unknown, 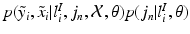 is approximated by its expected value given a multivariate Gaussian distribution on the patch
is approximated by its expected value given a multivariate Gaussian distribution on the patch 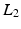 norm and a multivariate Gaussian distribution over the mapping
norm and a multivariate Gaussian distribution over the mapping 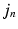
![$$\begin{aligned} p(\tilde{y}_i,\tilde{x}_i|l^I_{i},j_n,\mathcal {X}, \mathcal {\theta })p(j_n|l^I_{i},\mathcal {\theta })&\approx E[p(\tilde{y}_i,\tilde{x}_i|l^I_{i},j_n,\mathcal {X}, \mathcal {\theta })p(j_n|l^I_{i},\mathcal {\theta })]\nonumber \\&=\sum _{j^*\in \mathcal {N}_s}p(\tilde{y}_i,\tilde{x}_i|l^I_{i},j^*_n,\mathcal {X}, \mathcal {\theta })p(j^*_n|l^I_{i},\mathcal {\theta }). \end{aligned}$$](/wp-content/uploads/2016/09/A339424_1_En_2_Chapter_Equ1.gif)
Under this approximation and under the assumption of conditional independence between 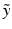 and
and 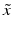 , then
, then  is defined as
is defined as
under the assumption of conditional independence between x and y, and
In Eq. (1),  is an integration neighbourhood of size
is an integration neighbourhood of size 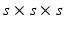 (again with
(again with 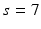 voxels) of an image similarity component (Eq. 2) and the registration uncertainty distance component (Eq. 3). In Eq. 2,
voxels) of an image similarity component (Eq. 2) and the registration uncertainty distance component (Eq. 3). In Eq. 2, 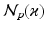 is a patch of size
is a patch of size 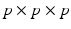 (with
(with 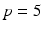 voxels) centred at location
voxels) centred at location 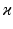 , and in Eq. 3,
, and in Eq. 3, 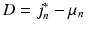 is a
is a 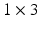 vector characterising the 3-dimensional components of a displacement from
vector characterising the 3-dimensional components of a displacement from 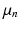 . Both the parameters
. Both the parameters 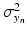 and
and 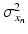 denote the sum of a local and a global normally distributed noise model (iid) between the observation
denote the sum of a local and a global normally distributed noise model (iid) between the observation 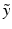 and the template
and the template 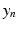 , defined as
, defined as
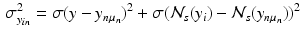 and equivalently for
and equivalently for 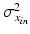 , with
, with 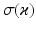 representing the standard deviation of
representing the standard deviation of 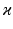 . Note that the
. Note that the 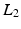 of the patch can here be used as all images
of the patch can here be used as all images 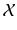 have been histogram matched to
have been histogram matched to 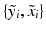 using a
using a 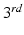 order polynomial fit after non-rigid registration. Finally,
order polynomial fit after non-rigid registration. Finally, 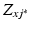 is a partition function enforcing
is a partition function enforcing
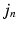 is unknown,
is unknown, 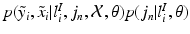 is approximated by its expected value given a multivariate Gaussian distribution on the patch
is approximated by its expected value given a multivariate Gaussian distribution on the patch 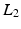 norm and a multivariate Gaussian distribution over the mapping
norm and a multivariate Gaussian distribution over the mapping 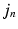
![$$\begin{aligned} p(\tilde{y}_i,\tilde{x}_i|l^I_{i},j_n,\mathcal {X}, \mathcal {\theta })p(j_n|l^I_{i},\mathcal {\theta })&\approx E[p(\tilde{y}_i,\tilde{x}_i|l^I_{i},j_n,\mathcal {X}, \mathcal {\theta })p(j_n|l^I_{i},\mathcal {\theta })]\nonumber \\&=\sum _{j^*\in \mathcal {N}_s}p(\tilde{y}_i,\tilde{x}_i|l^I_{i},j^*_n,\mathcal {X}, \mathcal {\theta })p(j^*_n|l^I_{i},\mathcal {\theta }). \end{aligned}$$](/wp-content/uploads/2016/09/A339424_1_En_2_Chapter_Equ1.gif)
(1)
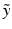 and
and 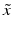 , then
, then 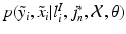 is defined as
is defined as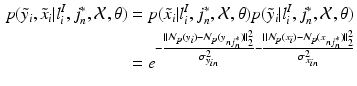
(2)
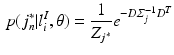
(3)
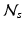 is an integration neighbourhood of size
is an integration neighbourhood of size 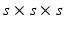 (again with
(again with 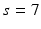 voxels) of an image similarity component (Eq. 2) and the registration uncertainty distance component (Eq. 3). In Eq. 2,
voxels) of an image similarity component (Eq. 2) and the registration uncertainty distance component (Eq. 3). In Eq. 2, 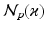 is a patch of size
is a patch of size 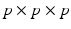 (with
(with 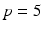 voxels) centred at location
voxels) centred at location 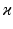 , and in Eq. 3,
, and in Eq. 3, 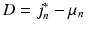 is a
is a 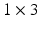 vector characterising the 3-dimensional components of a displacement from
vector characterising the 3-dimensional components of a displacement from 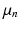 . Both the parameters
. Both the parameters 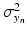 and
and 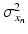 denote the sum of a local and a global normally distributed noise model (iid) between the observation
denote the sum of a local and a global normally distributed noise model (iid) between the observation 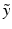 and the template
and the template 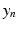 , defined as
, defined as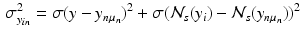
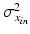 , with
, with 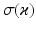 representing the standard deviation of
representing the standard deviation of 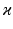 . Note that the
. Note that the 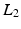 of the patch can here be used as all images
of the patch can here be used as all images 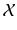 have been histogram matched to
have been histogram matched to 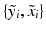 using a
using a 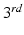 order polynomial fit after non-rigid registration. Finally,
order polynomial fit after non-rigid registration. Finally, 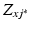 is a partition function enforcing
is a partition function enforcing