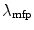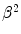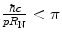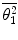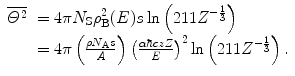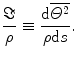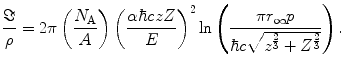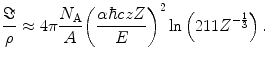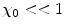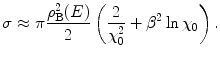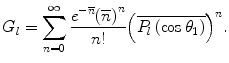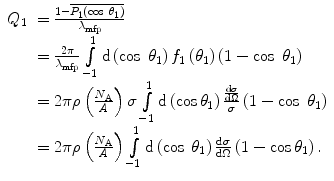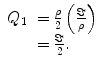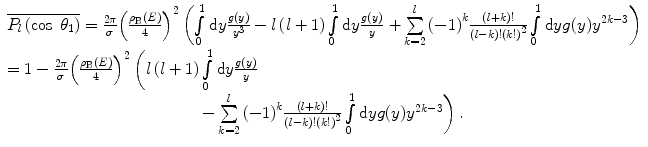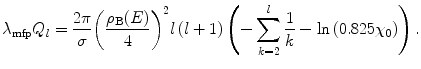(1)
Amersham, Buckinghamshire, UK
6.1 Introduction
6.3.1 Introduction
6.3.3 Scattering Power
6.3.6 Williams Theory
6.3.7 Fermi–Eyges Theory
6.3.8 Molière Theory
Abstract
In the two previous chapters, we have considered singular scatter events only. However, the results of our derivations from these, whether for unscreened or screened charges, have shown that scatter is preferentially forward directed. As a consequence, when we consider the transport of a charged particle within a medium made up of multiple-scattering centres, we realise that a parallel beam of charged particles entering such a medium will generate an angular spectrum upon exiting. This is a consequence of multiple and primarily forward-directed scatters. We can, up to a point, assume that all of the scatters are forward directed and, providing a sufficient number of elastic scatters have occurred, apply the central-limit theorem and conclude that the spatial/angular distribution of projectiles after traversing a finite distance of medium is Gaussian. However, we cannot neglect the small, but non-negligible, contributions of large-angle multiple scatter which will add ‘tails’ to the Gaussian.
In this chapter, we consider the statistics of multiple elastic Coulomb scatter, introduce the concept of the scattering power and begin investigations of the contributions of atomic electrons to the multiple scattering of charged projectiles from atoms. The focus on the chapter will be upon our detailed derivation and examination of four theories which derive multiple scatter probability distribution functions: those of Goudsmit and Saunderson, Williams, Fermi and Eyges and the most advanced, that of Molière.
Note
For this chapter only, we will alter the nomenclature for the scattering angle: 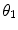 signifies the scattering angle after a single-scattering event, and
signifies the scattering angle after a single-scattering event, and 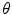 signifies the cumulative scattering angle after multiple single-scattering events.
signifies the cumulative scattering angle after multiple single-scattering events.
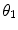 signifies the scattering angle after a single-scattering event, and
signifies the scattering angle after a single-scattering event, and 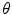 signifies the cumulative scattering angle after multiple single-scattering events.
signifies the cumulative scattering angle after multiple single-scattering events.6.1 Introduction
We have demonstrated that Coulomb elastic scatter from a bare, or unscreened, target leads to a 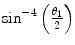 angular dependence which diverges as
angular dependence which diverges as 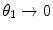 . This divergence was removed when we considered the more realistic case of the target being screened by a surrounding charge, as with the nucleus of the atom. This led to a
. This divergence was removed when we considered the more realistic case of the target being screened by a surrounding charge, as with the nucleus of the atom. This led to a 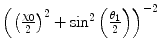 angular dependence, where
angular dependence, where 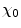 is the atomic electron screening angle. Despite the finite result of the latter, in both cases, the differential cross section is preferentially forward peaked, although it is the screened cross section that remains finite as
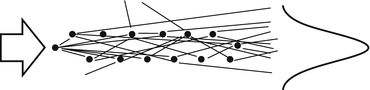
is the atomic electron screening angle. Despite the finite result of the latter, in both cases, the differential cross section is preferentially forward peaked, although it is the screened cross section that remains finite as 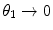 or, from (4.20), a large impact parameter. We shall now progress to the case of scattering within a medium containing multiple-scattering centres. These multiple interactions, combined with the forward-directed angular dependence of the scattering cross section, will lead to the overall tendency for charged particles traversing a medium to be scattered through repeated small scattering angles with the net scattering angle being described by a probability distribution function (pdf). This is shown conceptually in Fig. 6.1.
or, from (4.20), a large impact parameter. We shall now progress to the case of scattering within a medium containing multiple-scattering centres. These multiple interactions, combined with the forward-directed angular dependence of the scattering cross section, will lead to the overall tendency for charged particles traversing a medium to be scattered through repeated small scattering angles with the net scattering angle being described by a probability distribution function (pdf). This is shown conceptually in Fig. 6.1.
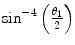 angular dependence which diverges as
angular dependence which diverges as 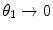 . This divergence was removed when we considered the more realistic case of the target being screened by a surrounding charge, as with the nucleus of the atom. This led to a
. This divergence was removed when we considered the more realistic case of the target being screened by a surrounding charge, as with the nucleus of the atom. This led to a  angular dependence, where
angular dependence, where  is the atomic electron screening angle. Despite the finite result of the latter, in both cases, the differential cross section is preferentially forward peaked, although it is the screened cross section that remains finite as
is the atomic electron screening angle. Despite the finite result of the latter, in both cases, the differential cross section is preferentially forward peaked, although it is the screened cross section that remains finite as 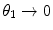 or, from (4.20), a large impact parameter. We shall now progress to the case of scattering within a medium containing multiple-scattering centres. These multiple interactions, combined with the forward-directed angular dependence of the scattering cross section, will lead to the overall tendency for charged particles traversing a medium to be scattered through repeated small scattering angles with the net scattering angle being described by a probability distribution function (pdf). This is shown conceptually in Fig. 6.1.
or, from (4.20), a large impact parameter. We shall now progress to the case of scattering within a medium containing multiple-scattering centres. These multiple interactions, combined with the forward-directed angular dependence of the scattering cross section, will lead to the overall tendency for charged particles traversing a medium to be scattered through repeated small scattering angles with the net scattering angle being described by a probability distribution function (pdf). This is shown conceptually in Fig. 6.1.
Fig. 6.1
Conceptual representation of multiple Coulomb scatter for a beam of charged projectiles incident from the left to an array of scattering centres. As a consequence of the angular distribution of the scattering, the tendency will be for multiple small-angle scatters for which the overall effect can be described by a probability distribution function as shown. Coulomb scatters through large angles are almost certainly, as a result of the low probability of large-angle scatter, due to a singular interaction between the charged particle and the scattering centre rather than a series of scatters of increasingly greater scatter angles with a negligible net probability of occurring
A charged particle observed to have been scattered through a large angle will have been almost exclusively due to a single interaction as the product of the probabilities of individual backscatters through smaller angles becomes insignificant. Hence, particles with a small net angular deviation from the initial direction are considered to have undergone multiple scatter. The pdf of the net scattering angle for multiple scatter is to be shown to be Gaussian, as would be expected from the central-limit theorem, with a width that is derivable from a fundamental single-scattering theory. On the other hand, those events observed at large scattering angles are considered to have undergone single scatter. The intermediate state is that of plural scatter which while consisting of multiple-scattering events, the number of events being insufficient to yield the Gaussian pdf. Thus, the transitions from multiple to plural to single scatter follow with increasing scattering angles.
This chapter investigates the phenomenon of multiple elastic Coulomb scatter and its role in charged particle transport. The nature of multiple interactions between a moving charged particle and the atoms of a medium leads inevitably to a statistical description of the resultant distribution of charged particle directions. These interactions will occur at various distances along the paths and which are dependent upon the properties of the medium and particle and the probability of interaction, the latter described by the total cross section. The mean value of these distances, defined as the mean free path length is derived followed by the derivation of the descriptive statistics of multiple scatter. The mean-square scattering angle following a single scatter is calculated and then extended to that for multiple scatter on the basis of the central-limit theorem which assumes a Gaussian distribution function describing multiple scatter. This is then followed by the presentation of the scattering power, which describes the change in mean-square scattering angle per unit distance travelled in a medium.
Upon these foundations, the theory of multiple elastic Coulomb scatter is investigated in detail. Although there have been many theoretical descriptions of multiple scatter, four which have played roles in medical radiation dosimetry calculations are developed. The first is the Goudsmit–Saunderson theory which describes the scattering probability distribution function as a Legendre polynomial expansion. The second is that of Williams which is based upon the central-limit theorem as a descriptor of multiple scatter and incorporates a single-scatter pdf to model the ‘tails’ reflecting large-angle scattering events. The third, and one which has been used most prominently in radiotherapy dose calculations, is the Fermi–Eyges theory. This is based upon an explicit solution by Fermi to the diffusion equation describing multiple scatter, but which excluded the effects of the energy lost by the charged particles through collisions and which yielded a Gaussian pdf. Eyges subsequently modified this result to account for the effects of energy transfer at each scattering event and which affects the multiple scatter distribution as a function of depth. Finally, we conclude with the comprehensive Molière theory which describes in a single form the combination of multiple, plural and single scattering of charged particles.
As previously performed, numerical examples of 100 keV electrons and 250 MeV protons incident to carbon and calcium will be provided so as to establish the ranges of magnitudes of the discussed effects of relevance to medical applications.
6.2 Mean Free Path Length for Elastic Coulomb Scatter
6.2.1 Definition of the Mean Free Path Length
Consider a charged particle traversing a medium of physical density 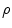 and atomic mass number A. We define the number density of scattering centres, i.e. the number of scattering centres (i.e. atoms) per unit volume, as
and atomic mass number A. We define the number density of scattering centres, i.e. the number of scattering centres (i.e. atoms) per unit volume, as
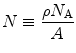
where N A is Avogadro’s number. The probability per unit path length of an interaction occurring between a charged particle and an atom of the medium is proportional to the number of scattering centres, 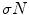 , where the constant of proportionality,
, where the constant of proportionality, 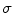 , is the total cross section of the interaction. For our discussion, the total cross section will be that for elastic Coulomb scatter only. There will be a statistical distribution of path lengths due to the stochastic nature of these interactions and the mean free path length is the reciprocal of the probability per unit path length:
, is the total cross section of the interaction. For our discussion, the total cross section will be that for elastic Coulomb scatter only. There will be a statistical distribution of path lengths due to the stochastic nature of these interactions and the mean free path length is the reciprocal of the probability per unit path length:
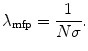
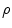 and atomic mass number A. We define the number density of scattering centres, i.e. the number of scattering centres (i.e. atoms) per unit volume, as
and atomic mass number A. We define the number density of scattering centres, i.e. the number of scattering centres (i.e. atoms) per unit volume, as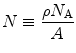
(6.1)
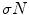 , where the constant of proportionality,
, where the constant of proportionality, 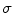 , is the total cross section of the interaction. For our discussion, the total cross section will be that for elastic Coulomb scatter only. There will be a statistical distribution of path lengths due to the stochastic nature of these interactions and the mean free path length is the reciprocal of the probability per unit path length:
, is the total cross section of the interaction. For our discussion, the total cross section will be that for elastic Coulomb scatter only. There will be a statistical distribution of path lengths due to the stochastic nature of these interactions and the mean free path length is the reciprocal of the probability per unit path length: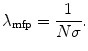
(6.2)
6.2.2 Mean Free Path Length Between Elastic Coulomb Scatters
The total elastic Coulomb scattering cross section is given by
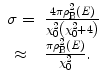
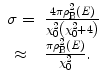
(6.3)
Substituting (6.3) into (6.2) yields the expression for the mean free path length between elastic Coulomb scatters from atoms (including the effects of atomic electron screening),
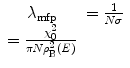
or by expanding the definitions of the atomic electron screening angle, scattering centre density and the Bohr collision diameter, we obtain the nonrelativistic result
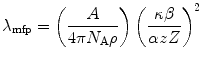
where 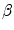 is the projectile velocity normalised to that of light. Looking at the functional dependence of (6.5), we see that the mean free path length increases with increasing screening and decreases with increased Coulomb interaction with the scattering centre. Figure 6.2 shows the variation of
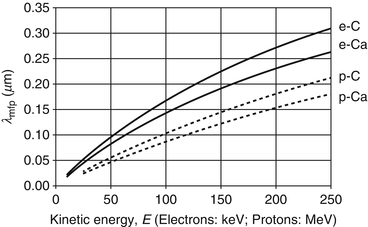
is the projectile velocity normalised to that of light. Looking at the functional dependence of (6.5), we see that the mean free path length increases with increasing screening and decreases with increased Coulomb interaction with the scattering centre. Figure 6.2 shows the variation of 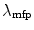 as a function of kinetic energy for nonrelativistic electrons and protons in carbon and calcium.
as a function of kinetic energy for nonrelativistic electrons and protons in carbon and calcium.
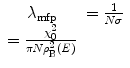
(6.4)
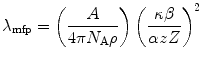
(6.5)
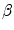 is the projectile velocity normalised to that of light. Looking at the functional dependence of (6.5), we see that the mean free path length increases with increasing screening and decreases with increased Coulomb interaction with the scattering centre. Figure 6.2 shows the variation of
is the projectile velocity normalised to that of light. Looking at the functional dependence of (6.5), we see that the mean free path length increases with increasing screening and decreases with increased Coulomb interaction with the scattering centre. Figure 6.2 shows the variation of 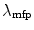 as a function of kinetic energy for nonrelativistic electrons and protons in carbon and calcium.
as a function of kinetic energy for nonrelativistic electrons and protons in carbon and calcium.
Fig. 6.2
Mean free path lengths between elastic Coulomb scatters from atoms for electrons and protons in carbon and calcium
It can be seen from Fig. 6.2 that the traversing of even 1 cm of tissue will result in several thousands of Coulomb interactions. This mean number of interactions will be calculated explicitly shortly.
6.3 Multiple Elastic Coulomb Scatter
6.3.1 Introduction
The transport of charged particles within a medium is, as a result of the forward-directed elastic Coulomb scatter and the variation of the mean free path length with energy, described stochastically due to multiple scattering from atoms. Hence, a pdf in scattering angle (or its projection onto orthogonal planes) is used to characterise the nature of this scattering. In this section, we consider four statistical multiple-scattering theories that have played, and some continue to play, significant roles in medical radiation practice. Their foundations all lie within the Rutherford cross section with additional considerations limited to atomic electron screening.
As shown in our previous derivation of the total elastic Coulomb scatter cross section, the role of finite nuclear size is often limited for medical radiation applications. The interested reader can find an examination of its effect in the paper by Cooper and Rainwater (1955).
6.3.2 Scattering Angle Statistics
6.3.2.1 Normalised Single-Scatter Distribution
As multiple scatter is the result of large numbers of single-scattering events, we look first at the descriptive statistics of single scatter. Two major quantities of interest in the description of multiple scatter will be the mean-square scattering angle, 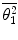 , and the root-mean-square scattering angle,
, and the root-mean-square scattering angle, 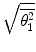 . In order to evaluate these, we first define the normalised single-scatter angular distribution,
. In order to evaluate these, we first define the normalised single-scatter angular distribution,
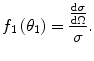
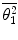 , and the root-mean-square scattering angle,
, and the root-mean-square scattering angle, 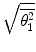 . In order to evaluate these, we first define the normalised single-scatter angular distribution,
. In order to evaluate these, we first define the normalised single-scatter angular distribution,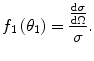
(6.6)
6.3.2.2 Mean-Square, Root-Mean Square and Mean Scattering Angles
The mean-square single-scattering angle is given by the integral of the square of the scattering angle weighted by the single-scatter distribution function,
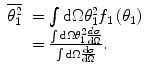
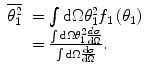
(6.7)
We will use the unscreened (Rutherford) differential cross section and account for atomic electron screening through the imposition of the atomic electron screening angle 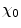 as the lower limit to the integration. Further, as the scattering cross section is very highly peaked for
as the lower limit to the integration. Further, as the scattering cross section is very highly peaked for 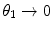 , we can use the small-angle approximation1 (i.e. the differential cross section is proportional to
, we can use the small-angle approximation1 (i.e. the differential cross section is proportional to 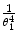 and
and 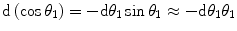 ). We now consider an expression for the upper integration limit which will be dictated by the finite nuclear size as suggested in our earlier discussion of the nuclear form factor in Chap. 5. For all natures of distributed charges,
). We now consider an expression for the upper integration limit which will be dictated by the finite nuclear size as suggested in our earlier discussion of the nuclear form factor in Chap. 5. For all natures of distributed charges, 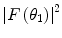 drops off rapidly with the dimensionless variable which is proportional to the 3-vector momentum transfer,
drops off rapidly with the dimensionless variable which is proportional to the 3-vector momentum transfer, 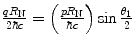 , so one could approximate the upper limit of the integral with the ratio
, so one could approximate the upper limit of the integral with the ratio 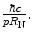 For low-energy electrons, the value of
For low-energy electrons, the value of 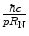 can be very large, e.g.
can be very large, e.g. 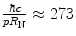 for 100 keV electrons incident to carbon. On the other hand, for 250 MeV protons incident to carbon, this upper limit angle is three orders-of-magnitude smaller,
for 100 keV electrons incident to carbon. On the other hand, for 250 MeV protons incident to carbon, this upper limit angle is three orders-of-magnitude smaller,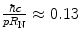 . As an alternative, we can set the upper limit of the integration over
. As an alternative, we can set the upper limit of the integration over 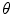 as equal to
as equal to 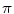 , reflecting the maximum scattering angle. Rossi (1952) has even suggested that one can set the upper limit to 1. In other calculations, the upper limit of other angular integrals has been set equal to
, reflecting the maximum scattering angle. Rossi (1952) has even suggested that one can set the upper limit to 1. In other calculations, the upper limit of other angular integrals has been set equal to 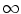 for mathematical convenience. Then, the mean-square single-scattering angle in the small-angle approximation is
for mathematical convenience. Then, the mean-square single-scattering angle in the small-angle approximation is
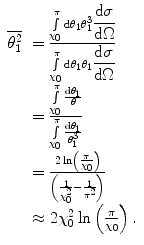
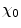 as the lower limit to the integration. Further, as the scattering cross section is very highly peaked for
as the lower limit to the integration. Further, as the scattering cross section is very highly peaked for 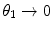 , we can use the small-angle approximation1 (i.e. the differential cross section is proportional to
, we can use the small-angle approximation1 (i.e. the differential cross section is proportional to 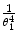 and
and 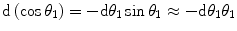 ). We now consider an expression for the upper integration limit which will be dictated by the finite nuclear size as suggested in our earlier discussion of the nuclear form factor in Chap. 5. For all natures of distributed charges,
). We now consider an expression for the upper integration limit which will be dictated by the finite nuclear size as suggested in our earlier discussion of the nuclear form factor in Chap. 5. For all natures of distributed charges, 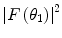 drops off rapidly with the dimensionless variable which is proportional to the 3-vector momentum transfer,
drops off rapidly with the dimensionless variable which is proportional to the 3-vector momentum transfer, 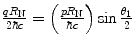 , so one could approximate the upper limit of the integral with the ratio
, so one could approximate the upper limit of the integral with the ratio 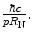 For low-energy electrons, the value of
For low-energy electrons, the value of 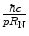 can be very large, e.g.
can be very large, e.g. 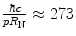 for 100 keV electrons incident to carbon. On the other hand, for 250 MeV protons incident to carbon, this upper limit angle is three orders-of-magnitude smaller,
for 100 keV electrons incident to carbon. On the other hand, for 250 MeV protons incident to carbon, this upper limit angle is three orders-of-magnitude smaller,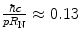 . As an alternative, we can set the upper limit of the integration over
. As an alternative, we can set the upper limit of the integration over 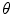 as equal to
as equal to 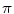 , reflecting the maximum scattering angle. Rossi (1952) has even suggested that one can set the upper limit to 1. In other calculations, the upper limit of other angular integrals has been set equal to
, reflecting the maximum scattering angle. Rossi (1952) has even suggested that one can set the upper limit to 1. In other calculations, the upper limit of other angular integrals has been set equal to 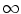 for mathematical convenience. Then, the mean-square single-scattering angle in the small-angle approximation is
for mathematical convenience. Then, the mean-square single-scattering angle in the small-angle approximation is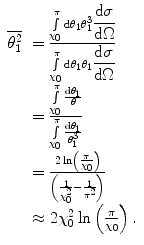
(6.8)
Using the Bohr form of the screening parameter from Table 5.1, the screening angle is, for the atomic number of the projectile much less than that of the target.2
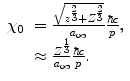
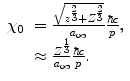
(6.9)
Substituting this into (6.8) gives
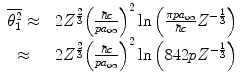
where the 3-vector momentum 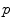 is given in units of
is given in units of 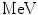 . This result contains an explicit momentum dependence within the argument of the logarithm. It would be useful if this dependence were not present. If, instead of using
. This result contains an explicit momentum dependence within the argument of the logarithm. It would be useful if this dependence were not present. If, instead of using 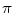 as the upper limit of integration, we were to replace it with
as the upper limit of integration, we were to replace it with 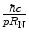 , then these momentum terms cancel
, then these momentum terms cancel
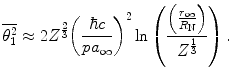
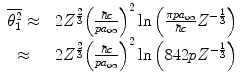
(6.10)
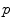 is given in units of
is given in units of 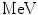 . This result contains an explicit momentum dependence within the argument of the logarithm. It would be useful if this dependence were not present. If, instead of using
. This result contains an explicit momentum dependence within the argument of the logarithm. It would be useful if this dependence were not present. If, instead of using 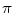 as the upper limit of integration, we were to replace it with
as the upper limit of integration, we were to replace it with 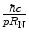 , then these momentum terms cancel
, then these momentum terms cancel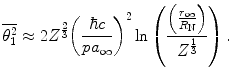
(6.11)
We can simplify the argument of the logarithm further by noting that the nuclear radius can be approximated by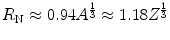 (in units of
(in units of 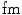 ), where we have used the approximation of
), where we have used the approximation of 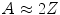 for light nuclei. In this case, (6.11) will reduce to
for light nuclei. In this case, (6.11) will reduce to
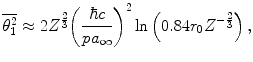
for which the Bohr radius is in units of fm. Then, In 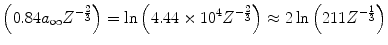 , which leads to
, which leads to
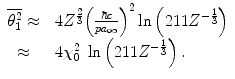
 (in units of
(in units of  ), where we have used the approximation of
), where we have used the approximation of 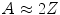 for light nuclei. In this case, (6.11) will reduce to
for light nuclei. In this case, (6.11) will reduce to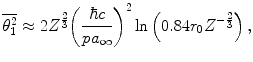
(6.12)
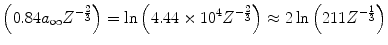 , which leads to
, which leads to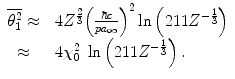
(6.13)
As has been noted by Jackson (1999), the multiplier within the logarithm of (6.13) varies between the derivations provided by different authors. Whereas our result has a value of 211, he derived a value of 204, and Rossi (1952) quoted a value of 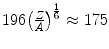 also with the approximation of
also with the approximation of 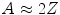 . However, as all of these multipliers reside within the argument of the logarithm, the differences between the magnitudes of the mean-square angles calculated with these multipliers are about only 4 % for elements with the low atomic numbers typical of tissue.
. However, as all of these multipliers reside within the argument of the logarithm, the differences between the magnitudes of the mean-square angles calculated with these multipliers are about only 4 % for elements with the low atomic numbers typical of tissue.
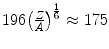 also with the approximation of
also with the approximation of 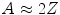 . However, as all of these multipliers reside within the argument of the logarithm, the differences between the magnitudes of the mean-square angles calculated with these multipliers are about only 4 % for elements with the low atomic numbers typical of tissue.
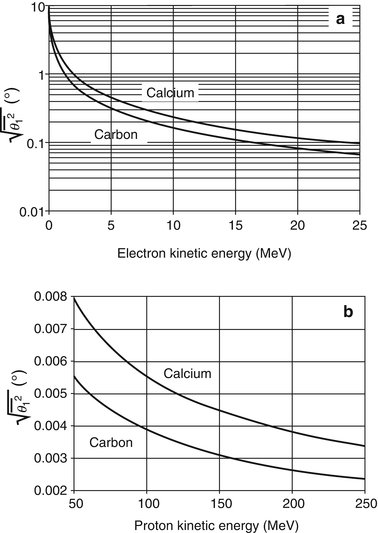
. However, as all of these multipliers reside within the argument of the logarithm, the differences between the magnitudes of the mean-square angles calculated with these multipliers are about only 4 % for elements with the low atomic numbers typical of tissue.Figure 6.3 shows the root-mean-square (RMS) single-scattering angle (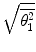 ) as a function of electron and proton kinetic energies typical of medical use in carbon and calcium as calculated from (6.13).3 There are a number of factors to note from this Figure. First,
) as a function of electron and proton kinetic energies typical of medical use in carbon and calcium as calculated from (6.13).3 There are a number of factors to note from this Figure. First, 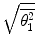 for both projectiles is higher for calcium than carbon, reflecting the atomic number dependence of the scattering cross section. Second,
for both projectiles is higher for calcium than carbon, reflecting the atomic number dependence of the scattering cross section. Second, 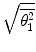 decreases with increasing energy as slower particles are more easily deflected. Third,
decreases with increasing energy as slower particles are more easily deflected. Third, 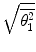 is markedly higher for electrons than for protons as lighter particles are more easily deflected.
is markedly higher for electrons than for protons as lighter particles are more easily deflected.
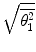 ) as a function of electron and proton kinetic energies typical of medical use in carbon and calcium as calculated from (6.13).3 There are a number of factors to note from this Figure. First,
) as a function of electron and proton kinetic energies typical of medical use in carbon and calcium as calculated from (6.13).3 There are a number of factors to note from this Figure. First, 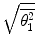 for both projectiles is higher for calcium than carbon, reflecting the atomic number dependence of the scattering cross section. Second,
for both projectiles is higher for calcium than carbon, reflecting the atomic number dependence of the scattering cross section. Second, 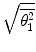 decreases with increasing energy as slower particles are more easily deflected. Third,
decreases with increasing energy as slower particles are more easily deflected. Third, 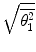 is markedly higher for electrons than for protons as lighter particles are more easily deflected.
is markedly higher for electrons than for protons as lighter particles are more easily deflected.
Fig. 6.3
Root-mean-square scattering angles for elastic Coulomb single scatter calculated for (a) electrons and (b) protons in carbon and calcium at kinetic energies typical of medical applications. Note that the ordinate of the plot in (a) is logarithmic
The mean single-scattering angle is
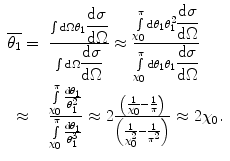
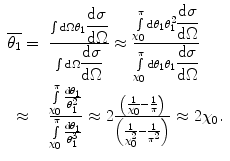
(6.14)
We will now anticipate our later derivations of the multiple-scattering theories and note that as the successive collisions are statistically independent,4 following 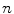 scatters with n large, the central-limit theorem leads to the result that the distribution in scattering angle approaches the Gaussian with a variance given by
scatters with n large, the central-limit theorem leads to the result that the distribution in scattering angle approaches the Gaussian with a variance given by 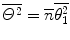 , where
, where 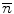 is the mean number of scatterings. From the definition of the probability of an elastic Coulomb scatter occurring per unit path length, one can calculate the mean number of such scatters, while traversing a medium of thickness s and physical density
is the mean number of scatterings. From the definition of the probability of an elastic Coulomb scatter occurring per unit path length, one can calculate the mean number of such scatters, while traversing a medium of thickness s and physical density 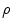 is
is
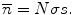
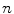 scatters with n large, the central-limit theorem leads to the result that the distribution in scattering angle approaches the Gaussian with a variance given by
scatters with n large, the central-limit theorem leads to the result that the distribution in scattering angle approaches the Gaussian with a variance given by 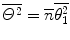 , where
, where 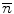 is the mean number of scatterings. From the definition of the probability of an elastic Coulomb scatter occurring per unit path length, one can calculate the mean number of such scatters, while traversing a medium of thickness s and physical density
is the mean number of scatterings. From the definition of the probability of an elastic Coulomb scatter occurring per unit path length, one can calculate the mean number of such scatters, while traversing a medium of thickness s and physical density 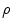 is
is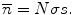
(6.15)
We now derive two expressions for 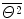 which will depend upon the nature of the
which will depend upon the nature of the 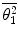 selected. For the case of
selected. For the case of 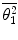 given by (6.8) :
given by (6.8) :
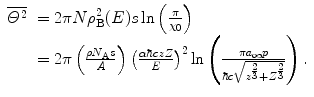
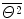 which will depend upon the nature of the
which will depend upon the nature of the 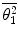 selected. For the case of
selected. For the case of 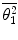 given by (6.8) :
given by (6.8) :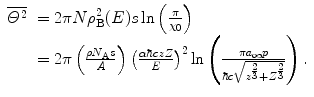
(6.16)
Although we will return to this discussion later, there are two functional dependencies that should be noted from these results:
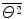 increases linearly with s. This observation shall need to be considered in the context of the fact that as the charged particle moves through the medium, it loses energy along its path and this linearity will be lost eventually along large path lengths as E in the denominator will decrease. For short path lengths and non-negligible energy loss, one can calculate for the arithmetic mean of the kinetic energy along the path length. For thicker path lengths, integration accounting for energy loss is required. This is performed in the Fermi–Eyges multiple-scattering theory to be considered later in this chapter.
increases linearly with s. This observation shall need to be considered in the context of the fact that as the charged particle moves through the medium, it loses energy along its path and this linearity will be lost eventually along large path lengths as E in the denominator will decrease. For short path lengths and non-negligible energy loss, one can calculate for the arithmetic mean of the kinetic energy along the path length. For thicker path lengths, integration accounting for energy loss is required. This is performed in the Fermi–Eyges multiple-scattering theory to be considered later in this chapter.
By ignoring the small contribution from the logarithmic term,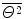 increases linearly with Z 2 as high atomic number media induce greater degrees of multiple scattering. This dependence upon the target’s atomic number will be investigated shortly as it neglects the separate contributions of the nucleus and of the atomic electrons to the scattering interaction. A more thorough examination is provided at the end of this chapter.
increases linearly with Z 2 as high atomic number media induce greater degrees of multiple scattering. This dependence upon the target’s atomic number will be investigated shortly as it neglects the separate contributions of the nucleus and of the atomic electrons to the scattering interaction. A more thorough examination is provided at the end of this chapter.
6.3.3 Scattering Power
6.3.3.1 Introduction
The above discussion considered the mean-square scattering angle associated with a single scatter and the resultant cumulative mean-square angle after traversing a given thickness of medium. What is often of practical interest in radiation transport and dosimetry calculations is the rate of change in the mean-square scattering angle with distance. As noted before, this will be the consequence of large numbers of single-scattering events which are each considered to be statistically independent.
There are two metrics that are useful in describing this change in mean-square scattering angle over distance travelled. The first is the linear scattering power defined as the derivative of the mean-square angle with total distance travelled, s,
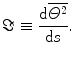
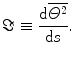
(6.18)
6.3.3.2 Spin-0 Projectiles
6.3.3.3 Spin-½ I: Mott Scattering of Electrons
In Chap. 4, we derived the differential cross section for the electric Coulomb scatter of an electron from an electrostatic field and which accounted for the intrinsic spin-½ of the electron. It was noted that the derivation would be the same for the positron.5 The resulting differential cross section in the small-angle limit is
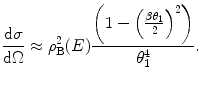
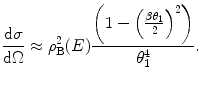
(6.22)
The Mott mean-square single-scattering angle is
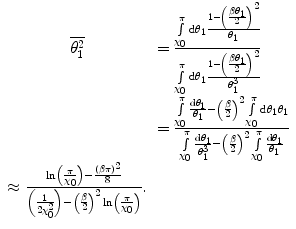
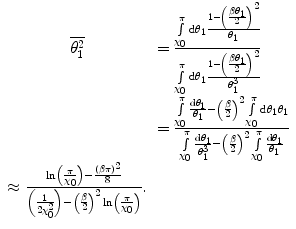
(6.23)
As expected, this result reduces to the spin-0 result of (6.8) for 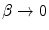 .
.
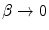 .
.The Mott total cross section is straightforward to derive and only the highlights are presented here,6
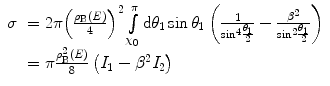
where
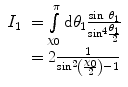
and
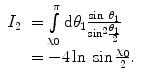
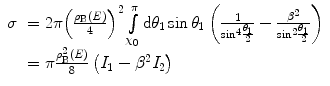
(6.24)
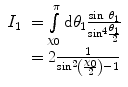
(6.25)
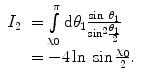
(6.26)
Note that in the nonrelativistic case, the Mott total cross section of (6.27) is in agreement with that of the spinless projectile given by (6.3). The Mott mass scattering power is
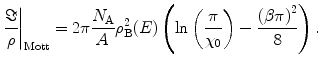
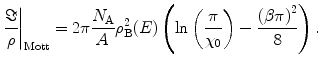
(6.28)
We can see that this result reduces to the previously derived spinless case of (6.20) as 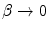 . Using the previous arguments regarding the argument of the logarithm, we can rewrite this result as
. Using the previous arguments regarding the argument of the logarithm, we can rewrite this result as
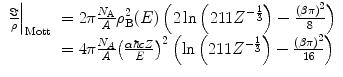
where, as the projectile is an electron, 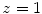 .
.
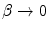 . Using the previous arguments regarding the argument of the logarithm, we can rewrite this result as
. Using the previous arguments regarding the argument of the logarithm, we can rewrite this result as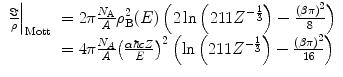
(6.29)
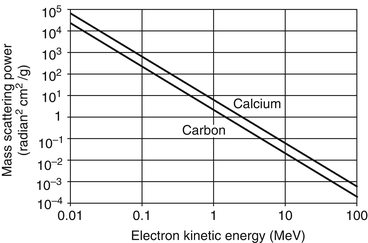
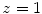 .
.The mass scattering power for electrons in carbon and calcium as a function of electron kinetic energy, as calculated from (6.29), is plotted in Fig. 6.4. As the ordinate and abscissa scales are both logarithmic, the linear appearances and negative slopes show that the 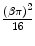 term, due to the electron’s intrinsic spin-½, has quite little influence upon the magnitude of the mass scattering power. This is evident by noting that
term, due to the electron’s intrinsic spin-½, has quite little influence upon the magnitude of the mass scattering power. This is evident by noting that 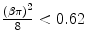 and that the magnitude of the term
and that the magnitude of the term 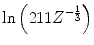 is equal to 4.75 and 4.35 for carbon and calcium, respectively.
is equal to 4.75 and 4.35 for carbon and calcium, respectively.
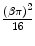 term, due to the electron’s intrinsic spin-½, has quite little influence upon the magnitude of the mass scattering power. This is evident by noting that
term, due to the electron’s intrinsic spin-½, has quite little influence upon the magnitude of the mass scattering power. This is evident by noting that 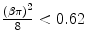 and that the magnitude of the term
and that the magnitude of the term 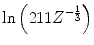 is equal to 4.75 and 4.35 for carbon and calcium, respectively.
is equal to 4.75 and 4.35 for carbon and calcium, respectively.
Fig. 6.4
Electron mass scattering power for carbon and calcium calculated from Eq. (6.29). Note that the contributions of the target’s atomic electrons are not included
A comparison of the magnitudes of the mass scattering powers of Fig. 6.4 with those calculated by the author (McParland 2010) using the exact expressions (i.e. without assumptions of 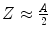 , small-angle approximation) and a different screening angle expression will show that there are differences in the numerical results of the scattering power calculations and that these are significant only at low energies.
, small-angle approximation) and a different screening angle expression will show that there are differences in the numerical results of the scattering power calculations and that these are significant only at low energies.
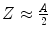 , small-angle approximation) and a different screening angle expression will show that there are differences in the numerical results of the scattering power calculations and that these are significant only at low energies.
, small-angle approximation) and a different screening angle expression will show that there are differences in the numerical results of the scattering power calculations and that these are significant only at low energies.6.3.4 Contributions of Atomic Electrons I
The above derivations have not considered the contribution to the elastic Coulomb scatter cross section that can be made by the atomic electrons (this is not the same as the screening of the nuclear electrostatic field by these electrons). These will increase the net electric charge and, hence, ‘effective’ atomic number seen by the projectile. An approximate method of allowing for this effect was suggested by Williams (1940) and Kulchitsky and Latyshev (1942) through the replacement of Z by 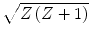 which reflects a coherent summation of
which reflects a coherent summation of 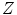 charges each with a single electric charge,
charges each with a single electric charge, 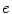 (i.e. the electron). This approximation will increase the scattering powers of carbon and calcium by 17 % and 5 %, respectively. This approach, however, assumes implicitly that the scattering cross sections for nuclear and electronic targets are the same which, clearly, they are not. Moreover, it implicitly assumes that the recoil kinetic energy far exceeds the atomic electron’s binding energy. A refinement proposed by Fano (1954), which allows for these effects, will be discussed later in this chapter in the context of the Molière multiple-scattering theory.
(i.e. the electron). This approximation will increase the scattering powers of carbon and calcium by 17 % and 5 %, respectively. This approach, however, assumes implicitly that the scattering cross sections for nuclear and electronic targets are the same which, clearly, they are not. Moreover, it implicitly assumes that the recoil kinetic energy far exceeds the atomic electron’s binding energy. A refinement proposed by Fano (1954), which allows for these effects, will be discussed later in this chapter in the context of the Molière multiple-scattering theory.
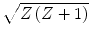 which reflects a coherent summation of
which reflects a coherent summation of 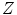 charges each with a single electric charge,
charges each with a single electric charge, 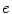 (i.e. the electron). This approximation will increase the scattering powers of carbon and calcium by 17 % and 5 %, respectively. This approach, however, assumes implicitly that the scattering cross sections for nuclear and electronic targets are the same which, clearly, they are not. Moreover, it implicitly assumes that the recoil kinetic energy far exceeds the atomic electron’s binding energy. A refinement proposed by Fano (1954), which allows for these effects, will be discussed later in this chapter in the context of the Molière multiple-scattering theory.
(i.e. the electron). This approximation will increase the scattering powers of carbon and calcium by 17 % and 5 %, respectively. This approach, however, assumes implicitly that the scattering cross sections for nuclear and electronic targets are the same which, clearly, they are not. Moreover, it implicitly assumes that the recoil kinetic energy far exceeds the atomic electron’s binding energy. A refinement proposed by Fano (1954), which allows for these effects, will be discussed later in this chapter in the context of the Molière multiple-scattering theory.6.3.5 Goudsmit–Saunderson Theory
6.3.5.1 Introduction
The charged particle of significant interest in medical dosimetry is the electron as it is set into motion through photon–matter interactions (i.e. photoelectric effect, Compton scatter, pair/triplet production) in tissue and is itself used directly as a means of therapy. As the electron has little mass, it will be subject to considerable magnitudes of scatter as was demonstrated in Fig. 6.3. Hence, it is appropriate that we begin our discussion of multiple-scattering theories with that by Goudsmit and Saunderson (1940) as it is exclusive to electrons and extends from our previous discussion of multiple, statistically independent scatters.
In the Goudsmit–Saunderson theory, the scattering angle is assumed to be sufficiently small so that the electron’s path length is equal to the thickness of the scatterer (in other words, the result is strictly valid only for thin foils or short discrete steps in a Monte Carlo simulation). The energy losses occurring through these collisions are neglected as the scatters are assumed to be perfectly elastic. One significant property of the Goudsmit–Saunderson theory is that it is not restricted to any underlying single-scattering differential cross section. As such, it uses the normalised single-scatter angle distribution of (6.6) from where we begin. Our derivation of the Goudsmit–Saunderson multiple-scattering pdf will follow the following three steps:
The pdf will be written as an expansion (infinite series) of Legendre polynomials with the series coefficients incorporate the Poisson distribution describing the probability of a given number of scatters occurring within a given path length (thus, using our previous derivation of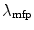 ).
).
The coefficients of this series are then determined using the screened Coulomb elastic single-scattering cross section as input.
The Goudsmit–Saunderson result is shown to be well represented by a Gaussian pdf with a variance evaluated in terms of the series.
6.3.5.2 Legendre Polynomial Expansions
Prior to the derivation, we first recall a property of the Legendre polynomials derived in Appendix C.2. As these polynomials are orthogonal, we can expand the scattering distribution into a series of Legendre polynomials. Consider the electron to have been scattered 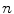 times, after which it is following a net direction given by an angle
times, after which it is following a net direction given by an angle 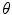 to its original trajectory. An additional property of the Legendre polynomial is that, if the scattering has azimuthal symmetry, the mean value of the Legendre polynomial after
to its original trajectory. An additional property of the Legendre polynomial is that, if the scattering has azimuthal symmetry, the mean value of the Legendre polynomial after 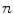 scatters will be equal to the nth power of its mean value following a single scatter. This can be shown readily by considering two sequential scatters. Let the electron be first scattered through an angle of deflection
scatters will be equal to the nth power of its mean value following a single scatter. This can be shown readily by considering two sequential scatters. Let the electron be first scattered through an angle of deflection 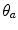 with a corresponding azimuthal angle,
with a corresponding azimuthal angle, 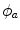 . The electron then undergoes a second scatter with an atom through the corresponding pair of angles
. The electron then undergoes a second scatter with an atom through the corresponding pair of angles 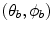 . The net scattering angle is thus
. The net scattering angle is thus 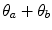 and
and
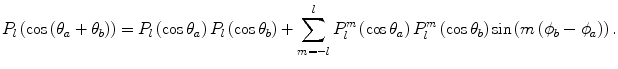
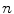 times, after which it is following a net direction given by an angle
times, after which it is following a net direction given by an angle 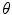 to its original trajectory. An additional property of the Legendre polynomial is that, if the scattering has azimuthal symmetry, the mean value of the Legendre polynomial after
to its original trajectory. An additional property of the Legendre polynomial is that, if the scattering has azimuthal symmetry, the mean value of the Legendre polynomial after 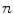 scatters will be equal to the nth power of its mean value following a single scatter. This can be shown readily by considering two sequential scatters. Let the electron be first scattered through an angle of deflection
scatters will be equal to the nth power of its mean value following a single scatter. This can be shown readily by considering two sequential scatters. Let the electron be first scattered through an angle of deflection 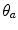 with a corresponding azimuthal angle,
with a corresponding azimuthal angle, 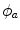 . The electron then undergoes a second scatter with an atom through the corresponding pair of angles
. The electron then undergoes a second scatter with an atom through the corresponding pair of angles 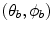 . The net scattering angle is thus
. The net scattering angle is thus 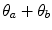 and
and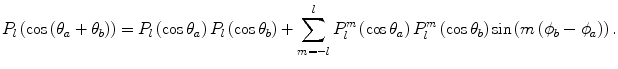
(6.30)
Averaging both sides gives
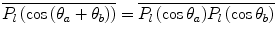
where, because of the axial symmetry, averaging over 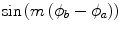 yields zero. As this result is for two sequential scatters, it can be extended to n sequential scatters to give the general result,
yields zero. As this result is for two sequential scatters, it can be extended to n sequential scatters to give the general result,
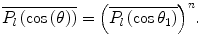
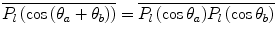
(6.31)
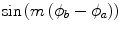 yields zero. As this result is for two sequential scatters, it can be extended to n sequential scatters to give the general result,
yields zero. As this result is for two sequential scatters, it can be extended to n sequential scatters to give the general result,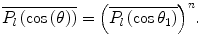
(6.32)
Recall our original introduction of the normalised single-scatter angular distribution of 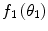 . This distribution may be conveniently expanded in a series of Legendre polynomials:
. This distribution may be conveniently expanded in a series of Legendre polynomials:
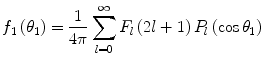
where the coefficients are given by
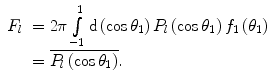
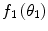 . This distribution may be conveniently expanded in a series of Legendre polynomials:
. This distribution may be conveniently expanded in a series of Legendre polynomials: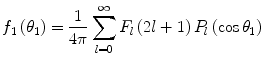
(6.33)
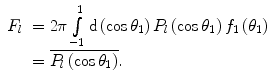
(6.34)
6.3.5.3 Multiple-Scattering Probability Distribution Function
Following the above expansion, one is then able to write the Goudsmit–Saunderson multiple scatter pdf as
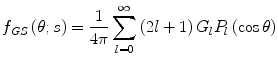
where 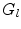 is the mean of the lth-order Legendre polynomial after the case of all possible values of n scatters, leading to the net scattering angle of
is the mean of the lth-order Legendre polynomial after the case of all possible values of n scatters, leading to the net scattering angle of  . 7 This is denoted as
. 7 This is denoted as
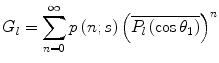
where 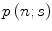 is the Poisson probability of n scatters occurring while the electron traverses a thickness s of the medium. (6.35) is normalised such that
is the Poisson probability of n scatters occurring while the electron traverses a thickness s of the medium. (6.35) is normalised such that
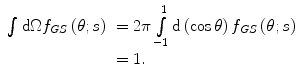
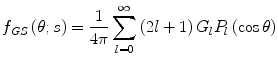
(6.35)
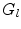 is the mean of the lth-order Legendre polynomial after the case of all possible values of n scatters, leading to the net scattering angle of
is the mean of the lth-order Legendre polynomial after the case of all possible values of n scatters, leading to the net scattering angle of 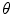 . 7 This is denoted as
. 7 This is denoted as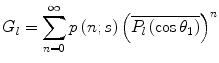
(6.36)
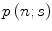 is the Poisson probability of n scatters occurring while the electron traverses a thickness s of the medium. (6.35) is normalised such that
is the Poisson probability of n scatters occurring while the electron traverses a thickness s of the medium. (6.35) is normalised such that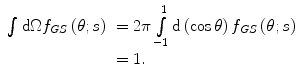
(6.37)
The mean of the lth-order Legendre polynomial term is
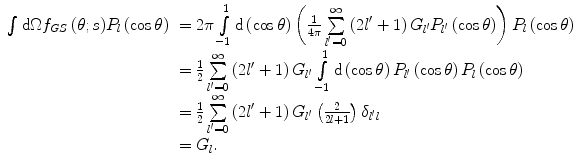
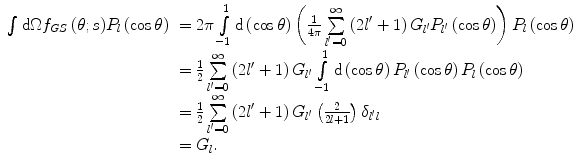
(6.38)
Hence, once the parameters 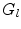 are known, all angular averages of the scattering distribution can be evaluated. Two examples of this result are
are known, all angular averages of the scattering distribution can be evaluated. Two examples of this result are
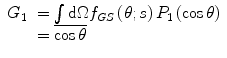 and
and
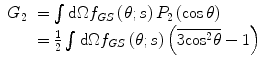 from which one obtains
from which one obtains
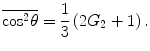
 are known, all angular averages of the scattering distribution can be evaluated. Two examples of this result are
are known, all angular averages of the scattering distribution can be evaluated. Two examples of this result are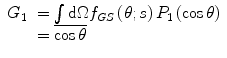
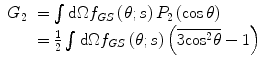
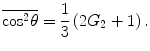
As a result, the evaluation of the scattering distribution 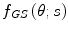 has been reduced to the evaluation of the mean values of the Legendre polynomials. However, it is necessary to recall that the definition of
has been reduced to the evaluation of the mean values of the Legendre polynomials. However, it is necessary to recall that the definition of 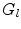 incorporates the probability of the electron undergoing n collisions, which is described by the associated Poisson distribution,
incorporates the probability of the electron undergoing n collisions, which is described by the associated Poisson distribution, 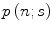 . In order to evaluate this probability, we recall the definition of the mean number of collisions,
. In order to evaluate this probability, we recall the definition of the mean number of collisions, 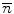 , over the thickness s given by (6.15).
, over the thickness s given by (6.15).
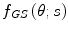 has been reduced to the evaluation of the mean values of the Legendre polynomials. However, it is necessary to recall that the definition of
has been reduced to the evaluation of the mean values of the Legendre polynomials. However, it is necessary to recall that the definition of 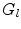 incorporates the probability of the electron undergoing n collisions, which is described by the associated Poisson distribution,
incorporates the probability of the electron undergoing n collisions, which is described by the associated Poisson distribution, 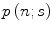 . In order to evaluate this probability, we recall the definition of the mean number of collisions,
. In order to evaluate this probability, we recall the definition of the mean number of collisions, 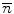 , over the thickness s given by (6.15).
, over the thickness s given by (6.15).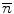 must be large in order to have the condition of multiple scattering be valid through the central-limit theorem. The probability that an electron will undergo n collisions while traversing s is
must be large in order to have the condition of multiple scattering be valid through the central-limit theorem. The probability that an electron will undergo n collisions while traversing s is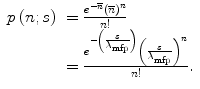
(6.39)
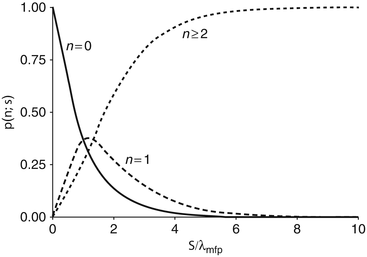
The probabilities of electron elastic scatter for 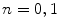 and
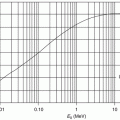
and 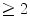 scatters are provided in Fig. 6.5 as functions of the ratio of the path length to the elastic scatter mean free path. The probability that no elastic scattering occurs becomes negligible for a thickness of
scatters are provided in Fig. 6.5 as functions of the ratio of the path length to the elastic scatter mean free path. The probability that no elastic scattering occurs becomes negligible for a thickness of 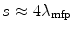 and greater, whereas the probability of
and greater, whereas the probability of 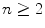 scatters approaches unity for
scatters approaches unity for 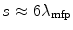 at about the same thickness. Both of these probabilities are monotonic functions of the ratio
at about the same thickness. Both of these probabilities are monotonic functions of the ratio 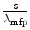 . To the contrary, the probability of a single scatter occurring is non-monotonic and reaches a maximum of about 0.35 at
. To the contrary, the probability of a single scatter occurring is non-monotonic and reaches a maximum of about 0.35 at 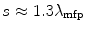 .
.
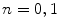 and
and 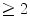 scatters are provided in Fig. 6.5 as functions of the ratio of the path length to the elastic scatter mean free path. The probability that no elastic scattering occurs becomes negligible for a thickness of
scatters are provided in Fig. 6.5 as functions of the ratio of the path length to the elastic scatter mean free path. The probability that no elastic scattering occurs becomes negligible for a thickness of 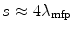 and greater, whereas the probability of
and greater, whereas the probability of 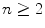 scatters approaches unity for
scatters approaches unity for 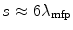 at about the same thickness. Both of these probabilities are monotonic functions of the ratio
at about the same thickness. Both of these probabilities are monotonic functions of the ratio 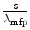 . To the contrary, the probability of a single scatter occurring is non-monotonic and reaches a maximum of about 0.35 at
. To the contrary, the probability of a single scatter occurring is non-monotonic and reaches a maximum of about 0.35 at 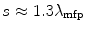 .
.
Fig. 6.5
The probability of electron elastic scatter occurring for n = 0, 1 and ≥2 scatters as a function of the ratio of the path length s to the elastic Coulomb scatter mean free path, λ mfp
By recalling the series expansion of the exponential, 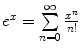 , we can rewrite (6.40) as
, we can rewrite (6.40) as
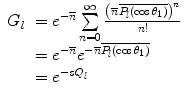
where we have defined the 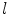 th-order transport coefficient as
th-order transport coefficient as
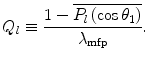
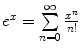 , we can rewrite (6.40) as
, we can rewrite (6.40) as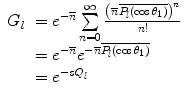
(6.41)
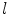 th-order transport coefficient as
th-order transport coefficient as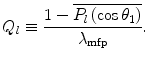
(6.42)
The Goudsmit–Saunderson scattering distribution is now of the form
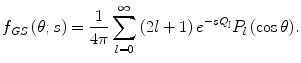
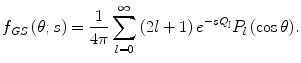
(6.43)
By assuming the unscreened Rutherford cross section, we refine further the integral of (6.44) by invoking the small-angle approximations of 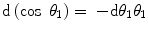 and
and 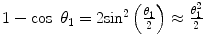 and setting the lower limit to be equal to the atomic electron screening angle,
and setting the lower limit to be equal to the atomic electron screening angle, 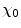 , to yield the expression
, to yield the expression
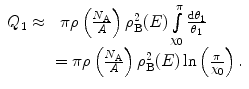
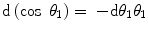 and
and 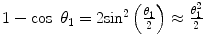 and setting the lower limit to be equal to the atomic electron screening angle,
and setting the lower limit to be equal to the atomic electron screening angle, 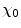 , to yield the expression
, to yield the expression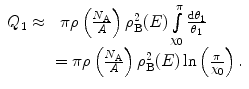
(6.45)
That is, the first-order transport coefficient is equal to one-half of the linear scattering power.
We now consider the fundamental single-scattering law that is introduced as input to the Goudsmit–Saunderson theory. We use the exponential-screening form derived in Chap. 5:
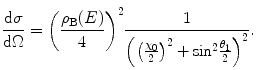
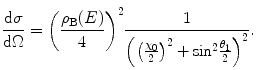
We will simplify the following derivations by defining the variable
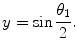
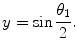
(6.47)
In this case, the total cross section for the single-scatter case can be written as
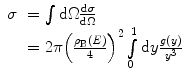
where 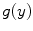 is the multiplicative factor accounting for atomic electron screening which, in our model, is
is the multiplicative factor accounting for atomic electron screening which, in our model, is
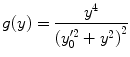
where 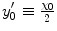 .
.
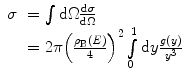
(6.48)
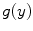 is the multiplicative factor accounting for atomic electron screening which, in our model, is
is the multiplicative factor accounting for atomic electron screening which, in our model, is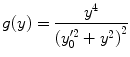
(6.49)
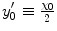 .
.We first evaluate the average values of the Legendre polynomials following a single collision and which are used in the transport coefficient. This is performed by the following expansion of the lth-order Legendre polynomial (taken by expanding the Rodrigues’ formula of (C.62)):
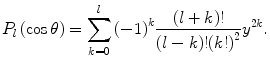
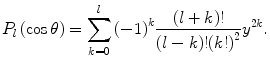
(6.50)
The average value after a single collision will be
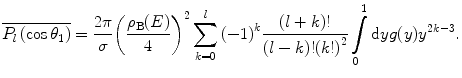
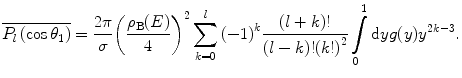
(6.51)
Recalling the definition of the transport coefficient, we have
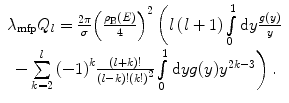
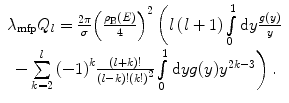
(6.53)
As the major contributions to the integral would be those from scattering events associated with large 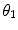 (i.e. small impact parameters and those cases of
(i.e. small impact parameters and those cases of  ), then
), then
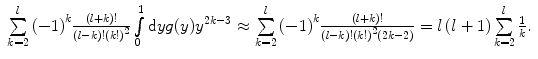
 (i.e. small impact parameters and those cases of
(i.e. small impact parameters and those cases of 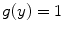 ), then
), then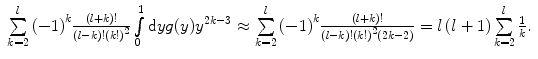
(6.54)
While Goudsmit and Saunderson provided the result of (6.54) without proof, Bethe (1953) provided a derivation of the expression. For convenience and interest, this proof is provided at the end of this chapter in a more transparent manner as part of our derivation of the Molière pdf.
However, the condition of 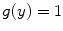 will not be met for very large values of
will not be met for very large values of 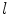 (corresponding to small
(corresponding to small 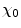 ). To demonstrate this, we crudely model the screening function in a discontinuous form
). To demonstrate this, we crudely model the screening function in a discontinuous form
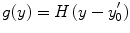
where 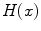 is the Heaviside function and
is the Heaviside function and 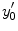 reflects the effect of the finite radial extent of the atom. Then,
reflects the effect of the finite radial extent of the atom. Then,
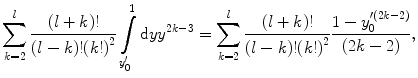
leading to the requirement of 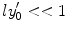 . Substituting (6.54) into (6.53) gives
. Substituting (6.54) into (6.53) gives
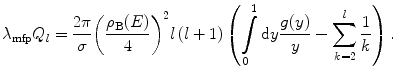
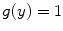 will not be met for very large values of
will not be met for very large values of 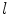 (corresponding to small
(corresponding to small 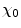 ). To demonstrate this, we crudely model the screening function in a discontinuous form
). To demonstrate this, we crudely model the screening function in a discontinuous form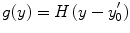
(6.55)
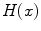 is the Heaviside function and
is the Heaviside function and 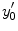 reflects the effect of the finite radial extent of the atom. Then,
reflects the effect of the finite radial extent of the atom. Then,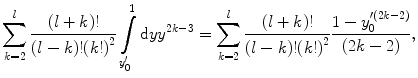
(6.56)
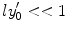 . Substituting (6.54) into (6.53) gives
. Substituting (6.54) into (6.53) gives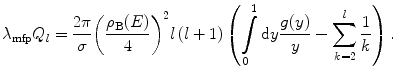
(6.57)
We now solve for the integral
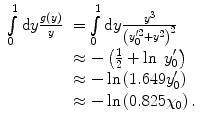
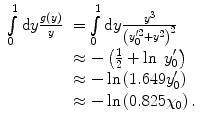
(6.58)
From these, the mean value of the Legendre polynomials following multiple scattering after a total path length s,
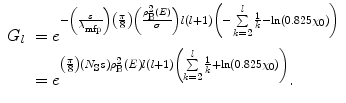
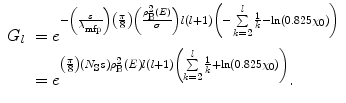
(6.60)
Thus, the Goudsmit–Saunderson scattering probability distribution function is
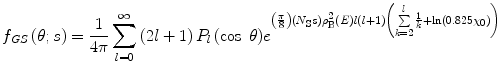
where 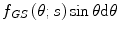 is the number of charged particles between
is the number of charged particles between 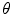 and
and 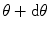 . The path length s means the distance travelled by the charged particle and does not consider the difference between it and the thickness of the medium that the particle traverses. This result is valid for not too large values of l and is also subject to the requirement that
. The path length s means the distance travelled by the charged particle and does not consider the difference between it and the thickness of the medium that the particle traverses. This result is valid for not too large values of l and is also subject to the requirement that
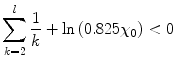
in order that the exponent of (6.61) remains necessarily negative.
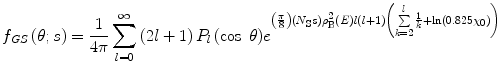
(6.61)
 is the number of charged particles between
is the number of charged particles between  and
and 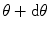 . The path length s means the distance travelled by the charged particle and does not consider the difference between it and the thickness of the medium that the particle traverses. This result is valid for not too large values of l and is also subject to the requirement that
. The path length s means the distance travelled by the charged particle and does not consider the difference between it and the thickness of the medium that the particle traverses. This result is valid for not too large values of l and is also subject to the requirement that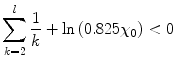
(6.62)
We note here that the general form of the Goudsmit–Saunderson result is
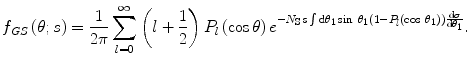
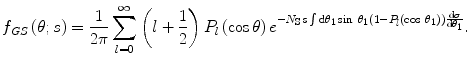
(6.63)
If we use the approximation, 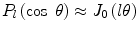 for
for ![$$ l>>1 $$” src=”/wp-content/uploads/2016/04/A306762_1_En_6_Chapter_IEq0006114.gif”></SPAN></p>
<div class='tao-gold-member'>
<div>Only gold members can continue reading. <a href='/login'>Log In</a> or <a href='/register'>Register</a> to continue</div>
</div>
<p></p>
<div class=]()
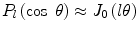 for
for Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree