, are usually observed and/or normalized in a large number of locations of a common space, denoted by 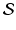 , across multiple time points
, across multiple time points 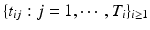 . Also,
. Also, 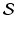 is often a compact subset of Euclidean space.
is often a compact subset of Euclidean space.
Methodology to handle longitudinal image data is still in its infancy, and further theoretical and practical development is much needed. Most existing methods focus on the analysis of univariate (or multivariate) variables measured longitudinally [4]. Many parametric mixed effects models including both fixed and random effects are the predominant approach for characterizing both the temporal correlations and random individual variations. Although there is a great interest in the analysis of functional data with various levels of hierarchical structures [7, 11, 18], only a handful of them [6, 17, 21] focused on the development of linear mixed models for longitudinal image data. Recently, there was some attempt on the development of hierarchical geodesic models on diffeomorphism for longitudinal shape analysis [15].
Specifically, FNMEM contains two major components including a random nonlinear association map for characterizing dynamic association between image data and covariates, and a spatial-temporal process for capturing large subject variation across both spatial and temporal domains. Because of its greater flexibility, FNMEM is generally more interpretable and parsimonious, and the predictions obtained from FNMEM extend more reliably outside the observed range of the data. We explicitly incorporate the spatial-temporal smoothness into our estimation procedure in order to accurately estimate the nonlinear association map and the spatial-temporal covariance operator. We also propose a global test statistic for testing the association map and construct its asymptotic simultaneous confidence band.
2 Method
2.1 Functional Nonlinear Mixed Effects Model
A functional nonlinear mixed effects model consists of two major components. The first one is a pointwise nonlinear mixed effects model given by
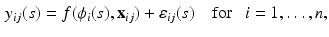
where 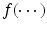 is a real-valued, differentiable nonlinear association map,
is a real-valued, differentiable nonlinear association map, 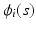 is a
is a 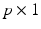 vector of subject-specific functions,
vector of subject-specific functions, 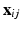 is p-dimensional covariate of interest, and
is p-dimensional covariate of interest, and 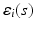 is the corresponding random error process. It is assumed that f has continuous second-order derivative with respect to
is the corresponding random error process. It is assumed that f has continuous second-order derivative with respect to 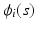 . For image data, it is typical that after normalization,
. For image data, it is typical that after normalization, 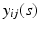 are measured at the same location for all subjects and exhibit both the within curve and between-curve dependence structure. Thus, without loss of generality, it is assumed that
are measured at the same location for all subjects and exhibit both the within curve and between-curve dependence structure. Thus, without loss of generality, it is assumed that 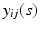 are observed on the M same grid points
are observed on the M same grid points ![$$\mathcal {S}_0=[0, 1]=\{s_m, 0=s_1\le s_2\cdots \le s_M=1\}$$](/wp-content/uploads/2016/09/A339424_1_En_63_Chapter_IEq13.gif) for all subjects and time points.
for all subjects and time points.
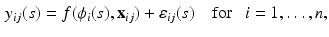
(1)
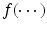 is a real-valued, differentiable nonlinear association map,
is a real-valued, differentiable nonlinear association map, 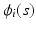 is a
is a 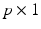 vector of subject-specific functions,
vector of subject-specific functions, 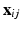 is p-dimensional covariate of interest, and
is p-dimensional covariate of interest, and 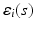 is the corresponding random error process. It is assumed that f has continuous second-order derivative with respect to
is the corresponding random error process. It is assumed that f has continuous second-order derivative with respect to 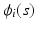 . For image data, it is typical that after normalization,
. For image data, it is typical that after normalization, 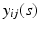 are measured at the same location for all subjects and exhibit both the within curve and between-curve dependence structure. Thus, without loss of generality, it is assumed that
are measured at the same location for all subjects and exhibit both the within curve and between-curve dependence structure. Thus, without loss of generality, it is assumed that 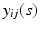 are observed on the M same grid points
are observed on the M same grid points ![$$\mathcal {S}_0=[0, 1]=\{s_m, 0=s_1\le s_2\cdots \le s_M=1\}$$](/wp-content/uploads/2016/09/A339424_1_En_63_Chapter_IEq13.gif) for all subjects and time points.
for all subjects and time points.The second one is a spatial-temporal process for modeling large variations across subject-specific functions 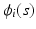 . Specifically,
. Specifically, 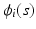 is modeled as
is modeled as
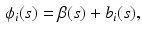
where 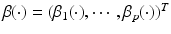 is a
is a 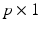 vector of fixed effect functions and
vector of fixed effect functions and 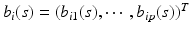 is a
is a 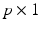 vector of random effect functions. In addition,
vector of random effect functions. In addition, 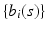 and
and 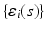 are independent and identical copies of SP(0,
are independent and identical copies of SP(0, 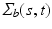 ) and SP(0,
) and SP(0, 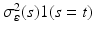 ) respectively, where SP(
) respectively, where SP(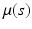 ,
, 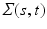 ) is a stochastic process (e.g., Gaussian process) with mean function
) is a stochastic process (e.g., Gaussian process) with mean function 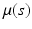 and covariance function
and covariance function 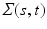 .
.
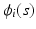 . Specifically,
. Specifically, 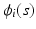 is modeled as
is modeled as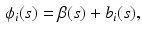
(2)
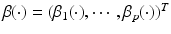 is a
is a 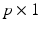 vector of fixed effect functions and
vector of fixed effect functions and 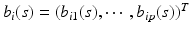 is a
is a 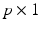 vector of random effect functions. In addition,
vector of random effect functions. In addition, 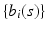 and
and 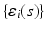 are independent and identical copies of SP(0,
are independent and identical copies of SP(0, 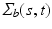 ) and SP(0,
) and SP(0, 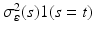 ) respectively, where SP(
) respectively, where SP(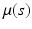 ,
, 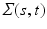 ) is a stochastic process (e.g., Gaussian process) with mean function
) is a stochastic process (e.g., Gaussian process) with mean function 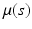 and covariance function
and covariance function 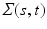 .
.2.2 An Example
Recently, nonlinear mixed effects models based on the Gompertz function have been used to characterize longitudinal white matter development during early childhood [3, 9, 14] The Gompertz function can be written as
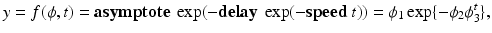 where
where 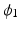 is asymptote,
is asymptote, 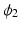 is delay, and
is delay, and 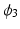 is
is 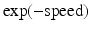 . Specifically, in [14], a nonlinear mixed effects model based on the Gompertz function is given by
. Specifically, in [14], a nonlinear mixed effects model based on the Gompertz function is given by
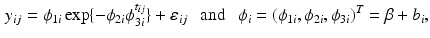
where 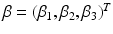 are fixed effects and
are fixed effects and 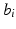 are random effects. For image data, an extension of model (3) is to consider a FNMEM as
are random effects. For image data, an extension of model (3) is to consider a FNMEM as
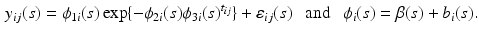
We will use model (4) to characterize the spatial-temporal dynamics of white-matter fiber tracts.
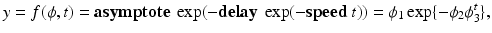
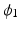 is asymptote,
is asymptote, 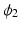 is delay, and
is delay, and 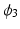 is
is 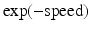 . Specifically, in [14], a nonlinear mixed effects model based on the Gompertz function is given by
. Specifically, in [14], a nonlinear mixed effects model based on the Gompertz function is given by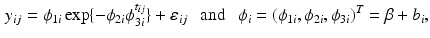
(3)
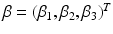 are fixed effects and
are fixed effects and 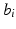 are random effects. For image data, an extension of model (3) is to consider a FNMEM as
are random effects. For image data, an extension of model (3) is to consider a FNMEM as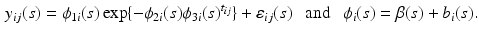
(4)
2.3 Estimation Procedure
The next interesting question is how to estimate the fixed effect and random effect functions of FNMEM. It should be noted that the estimation procedures used in [6, 17, 21] are not directly applicable here due to the nonlinear association map in (1).
Estimating the Fixed Effect Functions. At each grid point 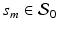 , we treat model (1) as a traditional nonlinear mixed effects model as
, we treat model (1) as a traditional nonlinear mixed effects model as
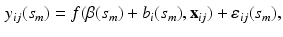
where 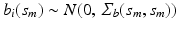 and
and 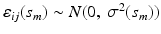 . Then, we calculate the maximum likelihood estimator of
. Then, we calculate the maximum likelihood estimator of 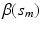 , denoted by
, denoted by 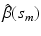 , across all
, across all 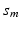 . Define
. Define 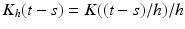 as the kernel function, where K is the Epanechnikov kernel, and
as the kernel function, where K is the Epanechnikov kernel, and 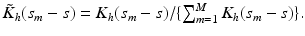 We calculate a kernel estimator of
We calculate a kernel estimator of 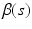 as:
as:
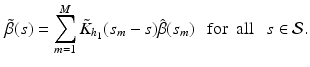
The bandwidth 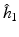 is selected using a leave-one-out cross-validation method.
is selected using a leave-one-out cross-validation method.
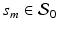 , we treat model (1) as a traditional nonlinear mixed effects model as
, we treat model (1) as a traditional nonlinear mixed effects model as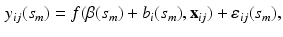
(5)
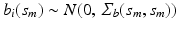 and
and 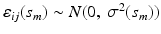 . Then, we calculate the maximum likelihood estimator of
. Then, we calculate the maximum likelihood estimator of 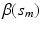 , denoted by
, denoted by 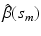 , across all
, across all 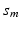 . Define
. Define 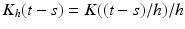 as the kernel function, where K is the Epanechnikov kernel, and
as the kernel function, where K is the Epanechnikov kernel, and 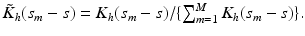 We calculate a kernel estimator of
We calculate a kernel estimator of 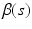 as:
as: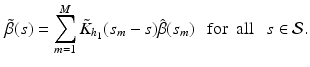
(6)
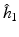 is selected using a leave-one-out cross-validation method.
is selected using a leave-one-out cross-validation method.Estimating the Covariance Operators. Under certain smoothness conditions on 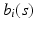 , we use local linear regression technique to estimate all
, we use local linear regression technique to estimate all 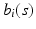 . Specifically, by using Taylor expansion for
. Specifically, by using Taylor expansion for 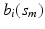 at
at 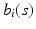 , we have
, we have
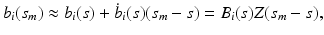 where
where 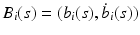 is a
is a 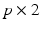 matrix and
matrix and 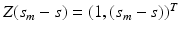 is a p dimensional vector, in which
is a p dimensional vector, in which 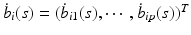 and
and 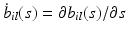 for
for 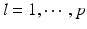 . For each i and s, we estimate
. For each i and s, we estimate 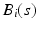 by minimizing the weighted nonlinear least squares [19]:
by minimizing the weighted nonlinear least squares [19]:
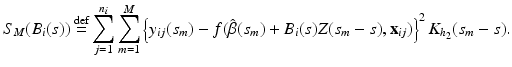 The optimal bandwidth
The optimal bandwidth 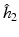 is selected using a leave-one-out cross-validation method, and an iteration algorithm is proposed to get the estimators. Finally, let
is selected using a leave-one-out cross-validation method, and an iteration algorithm is proposed to get the estimators. Finally, let 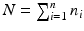 , we estimate
, we estimate 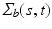 by using
by using
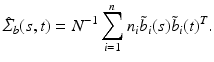 Functional Principal Component Analysis. With the empirical covariance
Functional Principal Component Analysis. With the empirical covariance 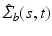 , we follow [13] and calculate the spectral decomposition as
, we follow [13] and calculate the spectral decomposition as
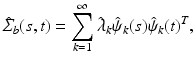 where
where 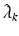 are estimated eigenvalues and
are estimated eigenvalues and 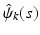 are their corresponding estimated eigenfunctions. Moreover, the k-th functional principal component scores can be computes by
are their corresponding estimated eigenfunctions. Moreover, the k-th functional principal component scores can be computes by 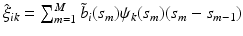 for
for 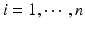 .
.
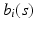 , we use local linear regression technique to estimate all
, we use local linear regression technique to estimate all 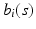 . Specifically, by using Taylor expansion for
. Specifically, by using Taylor expansion for 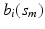 at
at 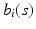 , we have
, we have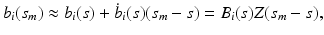
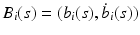 is a
is a  matrix and
matrix and 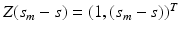 is a p dimensional vector, in which
is a p dimensional vector, in which 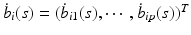 and
and 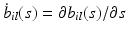 for
for 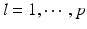 . For each i and s, we estimate
. For each i and s, we estimate 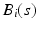 by minimizing the weighted nonlinear least squares [19]:
by minimizing the weighted nonlinear least squares [19]: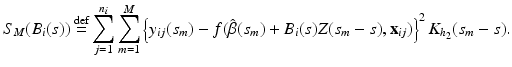
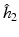 is selected using a leave-one-out cross-validation method, and an iteration algorithm is proposed to get the estimators. Finally, let
is selected using a leave-one-out cross-validation method, and an iteration algorithm is proposed to get the estimators. Finally, let  , we estimate
, we estimate  by using
by using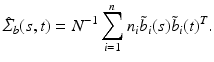
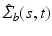 , we follow [13] and calculate the spectral decomposition as
, we follow [13] and calculate the spectral decomposition as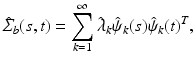
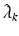 are estimated eigenvalues and
are estimated eigenvalues and 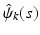 are their corresponding estimated eigenfunctions. Moreover, the k-th functional principal component scores can be computes by
are their corresponding estimated eigenfunctions. Moreover, the k-th functional principal component scores can be computes by 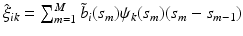 for
for  .
.2.4 Inference Procedure
The next interesting question is how to make statistical inference on the fixed effect functions of FNMEM.
Hypothesis Test. We focus on the linear hypothesis of 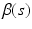 as follows
as follows
 where R is a
where R is a 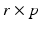 matrix with rank r, and
matrix with rank r, and 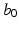 is a given
is a given 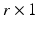 vector of functions. A global test statistic
vector of functions. A global test statistic 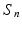 is given by
is given by
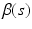 as follows
as follows
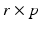 matrix with rank r, and
matrix with rank r, and 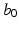 is a given
is a given 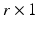 vector of functions. A global test statistic
vector of functions. A global test statistic 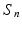 is given by
is given by
![$$ S_n=\int _0^1 \mathbf {d}(s)^T[R\hat{\varSigma }(s,s)R^T]^{-1}\mathbf {d}(s)ds, $$](/wp-content/uploads/2016/09/A339424_1_En_63_Chapter_Equ13.gif)




