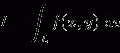(1)
Radiation Monitoring Devices Research Nuclear Medicine, Water town, Massachusetts, USA
1.1 Introduction
1.4 Definition
1.4.1 Roentgen
1.4.2 Fluence
1.4.3 Quality Factor
1.4.4 Radiation Dose
1.4.5 Rem
1.4.6 Energy
1.4.8 Radioactivity
1.4.9 Radioactive Decay
1.4.10 Positron
1.5.1 Alpha (α) Particle
1.5.2 Beta (β) Particles
1.5.3 Gamma (γ) Rays
1.7 Half-Value Layer
1.8 Neutrons
1.9.1 Elastic Scattering
1.9.3 Inelastic Scattering
1.11 Thermal Neutrons
1.12 Neutron Sources
1.13 Neutron Shielding
1.14 X-Rays
1.14.2 Beam Quality
1.16 Photoelectric Effect
1.17 Pair Production
1.19 Radionuclides
1.20.1 Cyclotron
1.20.2 Reactor
1.22 Summary
Abstract
The history of nuclear medicine—a branch of medicine dealing with radioactive materials and chemicals/die—is rich with the contributions from gifted scientists across different disciplines: physics, chemistry, engineering, and medicine [1–5]. The multidisciplinary nature of nuclear medicine makes it difficult for medical historians to determine the birth date of nuclear medicine. Many historians, however, consider the discovery of artificially produced radioisotopes, used for nuclear radiation therapy, which is a part of nuclear radiation physics as the most significant milestone in nuclear medicine. Indeed, nuclear radiation physics made a dramatic entry into medicine with the discovery of X-rays and natural radioactivity more than a century ago, and the potential for medical imaging and therapy based on these discoveries was very quickly recognized [6]. Nuclear radiation associated with nuclear energy is referred to as ionizing radiation. Figure 1.1 shows the schematic of nonionizing radiation and ionizing radiation and their uses in different fields.
1.1 Introduction
The history of nuclear medicine—a branch of medicine dealing with radioactive materials and chemicals/die—is rich with the contributions from gifted scientists across different disciplines: physics, chemistry, engineering, and medicine [1–5]. The multidisciplinary nature of nuclear medicine makes it difficult for medical historians to determine the birth date of nuclear medicine. Many historians, however, consider the discovery of artificially produced radioisotopes, used for nuclear radiation therapy, which is a part of nuclear radiation physics as the most significant milestone in nuclear medicine. Indeed, nuclear radiation physics made a dramatic entry into medicine with the discovery of X-rays and natural radioactivity more than a century ago, and the potential for medical imaging and therapy based on these discoveries was very quickly recognized [6]. Nuclear radiation associated with nuclear energy is referred to as ionizing radiation. Figure 1.1 shows the schematic of nonionizing radiation and ionizing radiation and their uses in different fields.
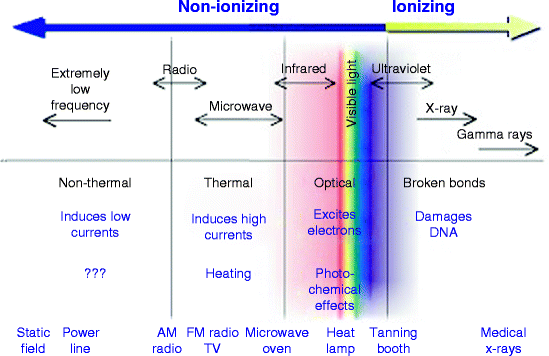

Fig. 1.1
The schematic of nonionizing and ionizing radiation (Courtesy: EPA, US)
All nuclear radiations are ionizing radiations, but the reverse is not true. As for example, X-ray is included among ionizing radiations even though it does not originate as a result of the disintegration of the atomic nuclei. On the other hand, during various nuclear processes, electromagnetic radiation is emitted from atomic nucleus [7]. Ionizing radiation, even though very small in energy compared to nonionizing radiation, is very damaging to life. As for example, both gamma rays and X-rays are ionizing radiation, and they can do great damage to cells in living organisms, disrupting cell function. Microwave, on the other hand, cannot cause ionization and cannot break atoms or molecular bonds typical of the molecules found in living things, but can excite the movements of atoms and molecules which is equivalent to heating the samples. Theoretical calculation shows that 1.5 million joules of nonionizing radiation will be required to kill a man. On the other hand, ionizing radiation like gamma rays and X-rays will be able to kill a man with a dose of only 300 J.
Everything on Earth is exposed to some sort of radiation either natural or man-made. 85.5 % of the total radiation (natural and artificial) is made up of 71 % telluric radiation and about 14.5 % cosmic radiation. Radiation particularly associated with nuclear medicine and the use of nuclear energy, along with X-rays, is ionizing. However, all the radiation sources do not have sufficient energy to interact with matter, especially the human body, and produce ions. Table 1.1 shows some of the rays that human beings encountered.
Table 1.1
Different radiation sources with respective frequencies and energies
Radiation | Typical frequency (s−1) | Typical energy (kJ/mol) |
|---|---|---|
Alpha (α) particles | 4.1 × 108 | |
Electromagnetic radiation | ||
Cosmic rays | 6 × 1021 s−1 | 2.4 × 109 ionizing radiation |
Gamma (γ) rays | 3 × 1020 s−1 | 1.2 × 108 ionizing radiation |
X-rays | 3 × 1017 s−1 | 1.2 × 105 |
Ultraviolet (UV) | 3 × 1015 s−1 | 1,200 nonionizing radiation |
Visible | 5 × 1014 s−1 | 200 nonionizing radiation |
Infrared (IR) | 3 × 1013 s−1 | 12 nonionizing radiation |
Microwaves | 3 × 109 s−1 | 1.2 × 10−3 nonionizing radiation |
Radio waves | 3 × 107 s−1 | 1.2 × 10−5 nonionizing radiation |
1.2 Ionizing Radiation and Consequences
The ionizing radiation, which has sufficient energy to interact with matter, especially in the human body is capable of producing ions, that is, it can eject an electron from an atom of the DNA (deoxyribonucleic acid) [8–11]. As a result, the bonding properties of the DNA atom change, causing a physical change of the DNA. Figure 1.2 shows the damaged molecule of DNA that regulates vital cell process.
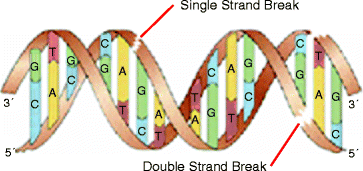

Fig. 1.2
The damaged molecules of DNA that regulates vital cell process (Courtesy: Canadian Nuclear Association Canada)
Thus the activity or the radioactivity of an ionizing radiation is very damaging to life. Therefore, the biological impact of terrestrial cosmic rays has been studied primarily to evaluate the damage to human body in air and space travel [12, 13]. Indeed, the detection of the ionizing radiation in nuclear medicine had been the primary goal of the research community since the discovery of artificial radioactivity in 1934 and the production of radionuclides in 1946.
1.3 Visual Demonstration of Radiation
1.
Spark Chamber: An ideal instrument for visual demonstration of the electrically charged particles from ionizing radiation is a spark chamber. The device is used mostly in particle physics for detecting electrically charged particles. It consists of metal plates placed in a sealed box filled with helium or neon or the mixture of the two. As charged particle moves through detector, it ionizes the gas between the plates. However, ionization remains invisible until a high voltage is applied between the plates. The high voltage creates a spark along the trajectory taken by the cosmic ray. Figure 1.3 shows a proton–antiproton interaction at 540 GeV. The picture shows particle tracks inside a spark chamber.


Fig. 1.3
A proton–antiproton interaction at 540 GeV, showing particle tracks inside a spark chamber (Photo courtesy: Wikimedia Commons)
2.
Bubble Chamber: Bubble chamber, invented by Donald Glaser, is a device to demonstrate the interactions of the charged particles received from an invisible radiation source. It is basically a vessel filled with superheated liquid. The trajectories of the energetic particles passing through the superheated liquid can be made visible and photographed [14]. Figure 1.4 shows the schematic of a simple bubble chamber conception.
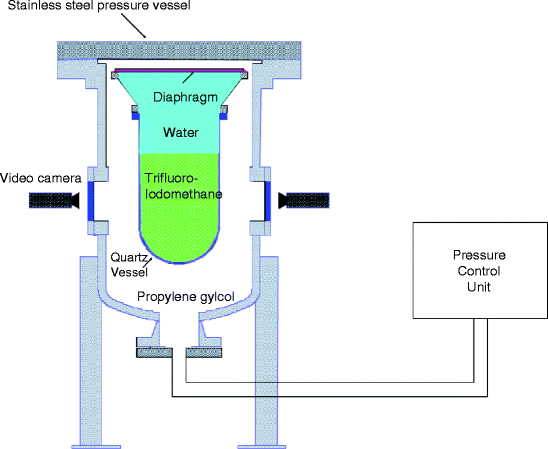

Fig. 1.4
The schematic of a simple bubble chamber conception (Courtesy: Fermi Lab. Chicago, IL.)
3.
Cloud Chamber: Another early invention to demonstrate the electrically charged particle track through a supersaturated gas of water or alcohol is the cloud chamber or the C.T.R. Wilson chamber. Energetic particles like alpha and beta when interact with supersaturated gas to form ions. A small electrostatic gradient is provided to sweep out ions between gas expansions. The apparatus in the modified form makes tracks of visible nuclear bullets in the form of cloud; hence, it is called a cloud chamber (shown in Fig. 1.5).


Fig. 1.5
The cloud-chamber photograph of very fast electron colliding with a stationary one (Courtesy: WIKI)
1.4 Definition
1.4.1 Roentgen
Roentgen (R) is defined as the energy dissipated by ionizing radiation in air. It is equivalent to the dissipation of 87.6 ergs per gram of dry air, which results in the generation of one electrostatic unit of charge per 0.001293 g (1 cm3 STP) of air.
The exposure value is expressed in coulomb per kilogram (C/kg), and the unit roentgen (R) is related to exposure as
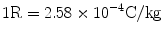
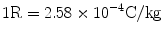
(1.1)
Therefore, we can say that the exposure is the effect of a given flux of gamma (γ) rays on a test volume of air. It is a function of the intensity of the source, geometry between the source and the test volume, and attenuation of the gamma rays that may take place between the two. The exposure of X-rays and γ-rays is measured on the assumptions that (a) the source is very small, (b) there is no attenuation in air between the source and the measured point, and (c) there is negligible scattering. When all of these conditions are satisfied, we can write the rate (dQ/dt) as
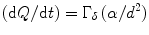
where Γ δ is defined as the exposure rate constant for the specific radioisotope of interest, α is the activity of the source and d is the distance in centimeter between the source and the measuring point, and the subscript δ applies to the energy of either that of the X-rays or γ-rays emitted by the source which has sufficient penetration energy [15]. The unit of exposure rate constant is expressed in (R∙cm2)/(h∙mCi). The value of Γ δ for some common isotope gamma-ray sources for δ = 0 is given in Table 1.2.
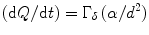
(1.2)
Table 1.2
Exposure rate constant for some radioisotope gamma-ray sources
Nuclide | Γ0 |
|---|---|
Antimony (Sb124) | 9.8 |
Cesium (Cs137) | 3.3 |
Cobalt (Co57) | 0.9 |
Cobalt (Co60) | 13.2 |
Iodine (I125) | ~0.7 |
Iodine (I131) | 2.2 |
Manganese (Mn54) | 4.7 |
Radium (Ra226) | 8.25 |
Sodium (Na22) | 12.0 |
Sodium (Na24) | 18.4 |
Technetium (Te99m) | 1.2 |
Zinc (Zn65) | 2.7 |
1.4.2 Fluence
Next we want to establish a relation between fluence and dose [17, 18]. The effective dose equivalent (H eq) can be written as
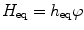
where ϕ = N/4πd 2. N is the number of photons or neutrons emitted by the source, d is the distance from the source, and h eq is the fluence to dose equivalent factor. However, the International Commission on Radiation Protection (ICRP) in its report 60 has introduced the definition of equivalent dose as H T,R which relates to the absorbed dose (D T,R) averaged over a tissue or organ T due to radiation R multiplied by a radiation weighting factor W R and can be expressed as
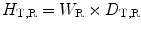
If there is a mixed radiation, then the total equivalent dose H T is given by
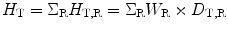
And the effective dose can be expressed in terms of equivalent dose H T and weighting factor as
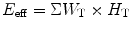
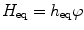
(1.3)
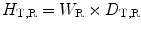
(1.4)
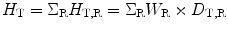
(1.5)
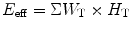
(1.6)
1.4.3 Quality Factor
Quality factor (QF) is defined as the relative damage per each radiation. Mathematically, it can be expressed as
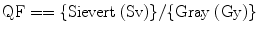
The SI unit of rad is gray (Gy), which is equivalent to 100 rads, and 1 Sv is equal to 100 rem. In nuclear medicine, 1 rad is equivalent to 100 ergs of energy per absorbed per gram of tissue. Different types of radiation do different amounts of biological damage, and we do need to know the effectiveness of an absorbed dose. The values for the Q-factors recommended by the International Commission on Radiological Protection (ICRP) are given in Table II [19].
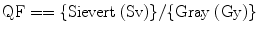
(1.7)
1.4.4 Radiation Dose
It is a measure of how much energy is deposited in a material from a source of radiation. The unit of dose is called rad. However, meaning of dose in nuclear medicine is different from the dose we mean during radiation, because in the former case, it records radiation emitting from within the body rather than radiation that is generated by external source.
1.4.5 Rem
In order to account for the differences in biological damage and risk among different types of radiation, a measurement unit called rem is established. Rem is defined as the amount of biological damage caused by ionization in human body. One rem of alpha (α) exposure is qualitatively same as 1 rem of beta (β) or gamma (γ) radiation. A committed dose equivalent (in rem) considers all of the dose equivalents caused by a radionuclide during 50 years of following intake. A committed dose equivalent is defined as a dose, which has occurred and will continue to occur because of radioactive material that has been taken into the body [20].
The other unit of ionizing radiation measurement is called curie (Ci), which is a measure of the number of atomic disintegration (3.7 × 1010) in a unit time. In other way, it can be defined as the activity of 1 g of pure radium (226Ra). However, the SI unit becquerel (Bq) is a more convenient practical unit used in the literature instead of curie (1 Bq = 2.073 × 10−11 Ci).
1.4.6 Energy
The radiation energy is measured in electron volt (eV). It is defined as the kinetic energy gained by an electron by its acceleration through a potential difference of 1 V. The SI unit of energy is expressed in joule (J).
One joule is equivalent to 6.241 × 1018 eV. The energy of radiation (E) can be related to wavelength (λ) of the photon as
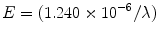
where λ is in meters and E is in eV. Table 1.3 presents the quality factors of different radiation and adsorbed dose.
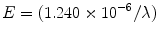
(1.8)
Table 1.3
For the Q-factors
Types of radiation | Quality factor | Adsorbed dose equal to a unit dose equivalent |
|---|---|---|
X-ray or gamma rays | 1 | 1 |
Beta particles | 1 | |
Neutrons and protons of unknown energy | 10 | 0.1 |
Singly charged particles of unknown energy with rest mass greater than 1 amu | 10 | |
Alpha particle | 20 | 0.05 |
Particles of multiple or unknown charge of unknown energy | 20 |
Table 1.4 presents the SI units of ionizing radiation, their conversion units, and the equivalence.
Table 1.4
Conversion unit
SI unit | Conversional unit | Equivalence |
|---|---|---|
Becquerel (Bq) | Curie (Ci) | 1 Bq =2.703 × 10−11 |
Gray (Gy) | Rad | 1 Gy =100 rad |
Coulombs per kilogram (C/kg) | Roentgen (R) | 1 C/kg = 3.9 × 103 R |
Sievert (Sv) | Rem | 1 Sv = 100 rem |
1.4.7 Relationship Between Kerma, Exposure, and Absorbed Dose
Kerma in medical science is defined as the kinetic energy which is released in the medium [21]. Or in other words, it is the ratio of the sum of the initial kinetic energy (KE) dE of all the charged ionizing particles (electrons and positrons) to the liberated by uncharged particles (photons) in a material of mass m. Mathematically, we can express kerma as
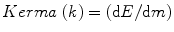
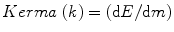
(1.9)
The kerma (k) is again related to the fluence (ϕ) of the photons and is expressed mathematically as
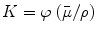
where 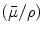 is the mass energy transfer coefficient for the medium averaged over the energy fluence spectrum of photons.
is the mass energy transfer coefficient for the medium averaged over the energy fluence spectrum of photons.
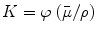
(1.10)
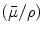 is the mass energy transfer coefficient for the medium averaged over the energy fluence spectrum of photons.
is the mass energy transfer coefficient for the medium averaged over the energy fluence spectrum of photons.The exposure (Χ r) [22] is defined as the ionization equivalent of the collision kerma (Κ) in air, and these two quantities are related as
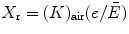
where e is the electronic charge (1.602 × 10−19 J) and 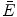 is the mean energy required to produce an ion pair in dry air. The SI unit of X r is coulomb (C) per kilogram (kg) (X r = C/kg) and the special unit is roentgen (R), where 1 R = 2.58 × 10−4 (C/kg).
is the mean energy required to produce an ion pair in dry air. The SI unit of X r is coulomb (C) per kilogram (kg) (X r = C/kg) and the special unit is roentgen (R), where 1 R = 2.58 × 10−4 (C/kg).
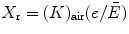
(1.11)
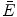 is the mean energy required to produce an ion pair in dry air. The SI unit of X r is coulomb (C) per kilogram (kg) (X r = C/kg) and the special unit is roentgen (R), where 1 R = 2.58 × 10−4 (C/kg).
is the mean energy required to produce an ion pair in dry air. The SI unit of X r is coulomb (C) per kilogram (kg) (X r = C/kg) and the special unit is roentgen (R), where 1 R = 2.58 × 10−4 (C/kg).Next, we want to find out a relation between the absorbed dose D and the fluence and hence to kerma. The dose D is closely approximated by
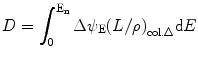
where ψ E is the differential distribution of fluence (ϕ) and is equal to (dψ E/dE) and (L/ρ)col.Δ is the restricted mass collision stopping power of a material [23, 24].
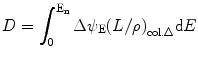
(1.12)
1.4.8 Radioactivity
Nuclear radiation can occur when a radioactive substance with unstable nucleus disintegrates. The nucleus is supposed to contain proton A and (A–Z) electrons and neutrons. Protons are positively charged, while the electrons are negatively charged. However, the nucleus cannot be composed of protons alone, since A is always equal to Z. Therefore, there must be some new particles, which together with protons constitute the nucleus. These particles are called neutrons, and they are neutral, having masses equal to 2.5m e, where m e is the mass of an electron. Neutrons are heavier than protons and 1.5m e heavier than the sum of the masses of proton and electron.
The discovery of neutrons and the investigation of its interaction with matter led to one of the most significant achievements in nuclear physics. In nuclear medicine, the ionizing radiation, which can damage the living tissues, is cleverly applied to diagnose (medical imaging) and damage (nuclear therapy) the cancerous cells without damaging the healthy tissues [25, 26].
All nuclei contain two types of elementary particles or nucleons, namely, protons and neutrons. A nuclide is a nucleus, which contains specified numbers of neutrons and protons. Therefore, nuclides are composite particles of nucleons. Nuclides that have the same number of protons but different numbers of neutrons are called isotopes. Certain combinations of neutrons and protons are unstable and break up spontaneously, a process referred to as radioactive decay. Such nuclides are called radionuclides or radioisotopes [27].
1.4.9 Radioactive Decay
All unstable nuclei, as well as nuclei in excited states, undergo spontaneous transformations leading to a change in their composition and/or internal energy of the nucleus. Such spontaneous nuclear processes are called radioactive processes since the radioactive decay [28] is governed by a fundamental law and is expressed mathematically as
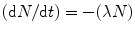
where (dN/dt) is differential equation of the number of radioactive nuclei N with time t in second and λ is the decay constant. The decay of a given isotope may lead to a daughter product. The average lifetime τ of a radioactive nucleus is the reciprocal of the disintegration constant λ [29].
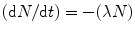
(1.13)
Another unit called as specific activity is also used to define the activity of a radioactive source per unit mass. It is expressed as
where M is molecular weight of the sample, A v is Avogadro’s number (=6.02 × 1023 nuclei/mol), and λ is radioactive decay constant (=(ln 2)/(half-life)).
(1.14)
Figure 1.6 shows the arrangements of protons (positively charged, red), neutrons (neutral, blue), and electrons (negatively charged, outside circle) in a helium atom. Helium atom (4He2) has 4 nucleon numbers (protons and neutrons together) and 2 nuclear charge number (proton number).
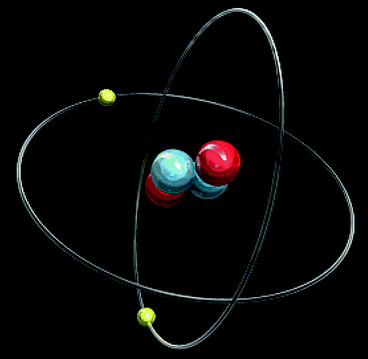

Fig. 1.6
The arrangements of protons, neutrons, and electrons (outside the orbit) in a helium atom (4He2)
The radioactive nucleus or the radioisotope (or radionuclide, a specific nucleus with given mass number A and electric charge Z, is sometimes called nuclide) normally decays by spontaneous emission of a particle from the nucleus. The emission may be alpha (α) particle, in which case we call it α-decay or the emission may emit an electron and we refer the case as β-decay. All these decays are statistical in character (Fig. 1.7).
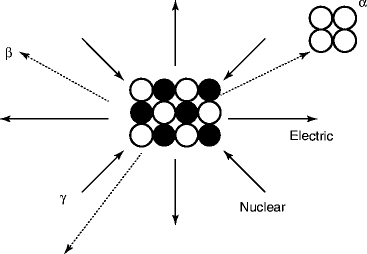

Fig. 1.7
The schematic of radioactive decay
In the beginning of the nineteenth century, the radioisotopes utilized were naturally occurring ones, such as radium-226 (226Ra), radium-224 (224Ra), radon-222 (222Rn), polonium-210 (210Po), tritium (hydrogen-3), and carbon-14 (14C). Joseph Hamilton was the first to use radioactive tracers to study circulatory physiology in the year 1937, and then in 1939 iodine-131 (131I) was used as radioisotope in nuclear medicine followed by technetium-99m (99mTc). In 1940, the first particle accelerator was built, and a number of radioisotopes were available.
All atomic nuclei can be broadly divided into two groups as stable and unstable or radioactive nuclei. The excess of neutrons in heavy nuclei 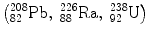 can be explained by Coulomb repulsion of protons. For β-stable nuclei, the relation between Z and A is described by the empirical formula
can be explained by Coulomb repulsion of protons. For β-stable nuclei, the relation between Z and A is described by the empirical formula
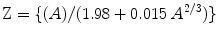
where Z is the charge number and A is the atomic number of the element. Nucleus in which this relation is violated is called a β-radioactive element. A β-radioactive element in course of time can decay a beta particle (an electron, β−, or a positron, β+). Neutron-rich nuclei, on the other hand, can emit an electron while proton rich nuclei can emit a positron [30].
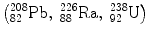 can be explained by Coulomb repulsion of protons. For β-stable nuclei, the relation between Z and A is described by the empirical formula
can be explained by Coulomb repulsion of protons. For β-stable nuclei, the relation between Z and A is described by the empirical formula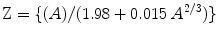
(1.15)
1.4.10 Positron
Positrons are antiparticles of electrons with identical mass and charge. It can also be identified as positively charged electron (β+). An unstable nucleus of some radioisotopes can emit positron due to excess number of protons and a positive charge, and then it can stabilize itself through the conversion of a proton to a neutron. Figure 1.8 shows a schematic of a positron-emitting radioisotope.


Fig. 1.8
A schematic of a positron-emitting radioisotope (Photo courtesy: Tutorial UCLA, CA)
When a positron comes in contact with an electron, the two particles annihilate and the mass of the two particles turned into two 511-keV gamma rays (γ-rays), and they are emitted on the two sides of the event (Fig. 1.9). One of the attractive aspects of e+–e− annihilation is the relative simplicity of the interaction. The two-body system decays into two back-to-back photons, each carrying an energy m e c 2. This feature has provided the basis of medical imaging techniques called positron emission tomography (PET). In PET, a positron-emitting radioisotope is introduced usually by injection, which promptly combines with a nearby electron resulting in the simultaneous emission of two identifiable gamma (γ) rays in opposite directions. These two gamma rays are detected in a PET camera.
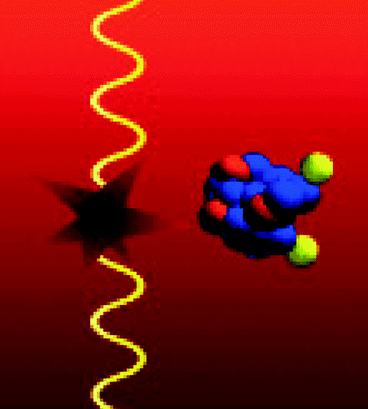

Fig. 1.9
The schematic of the 511-keV gamma rays emitted at 180° to each other (Photo courtesy Tutorial UCLA, CA)
According to quantum theory, the annihilation of positrons with electrons can produce high-energy photons—gamma quanta. Annihilation can take place directly or via the formation of positronium I, a state in which an electron and a positron form a light hydrogen atom bound by Coulomb attraction [31, 32]. In condensed matter, the interactions between positronium and the substrate can provide information about the details of the substrate structure via the effects on the momentum distribution at the instant of annihilation [33].
Figure 1.9 shows the conversion of two light energy photons in the form of γ-rays. The γ-rays on two opposite sides can easily escape from the human body and can be recorded by external detector/s [34]. Compact gamma (γ)-ray imager based on a silicon drift detector (SDD) coupled to a single scintillator crystal is very much in use in medical imaging system [35].
In medical imaging system, radiation detectors are used to diagnose cancerous cell. The benefit of a medical imaging examination in terms of its ability to yield an accurate diagnosis depends upon the quality of both the image acquisition and the image interpretation [36]. The special branch of the science dealing with medical imaging [37] and the diagnosis of the cancerous cells is called radiology, and the treatment for curative or adjuvant cancer treatment with radiation is called radiotherapy [38]. During the past century, both radiology and radiotherapy have grown tremendously due to the advances in image detector systems and computer technology [39].
1.5 Sources of Nuclear Radiation
Nuclear radiation arises from hundreds of different kinds of unstable atoms, and many of them exist in nature. As a matter of fact, in major cases under certain conditions, nuclear radiation is observed during nuclear reactions. Indeed, ionizing radiation, which damages living tissues, is emitted during the spontaneous decay of different kinds of atoms [40]. The principal kinds of ionizing radiation are (1) alpha (α) particles, (2) beta (β) particles, (3) gamma (γ) rays, and (4) X-rays.
1.5.1 Alpha (α) Particle
Alpha particles consist of two protons and two neutrons bound together into a helium particle identical to a helium nucleus, which is produced in the process of alpha decay. It has a very large mass (more than 700 times the mass of beta particle), charge, a very short range (less than a tenth of a millimeter inside the body), and a great destructive power of damaging fast-growing membrane and living cells [41]. Alpha decay is a radioactive process, which occurs in very heavy elements such as uranium (U), thorium (Th), and radium (Ra). The nuclei of these atoms are very neutron rich that make the emission of the alpha particle possible. When an atom emits an alpha particle during alpha decay, the mass number of the atom is decreased by four due to loss of the four nucleons in the alpha particle. The atomic number of the atom goes down exactly by two, as a result of the loss of two protons, and the atom becomes a new element. In contrast to beta decay, the fundamental interactions responsible for alpha decay are a balance between the electromagnetic force and nuclear force. Alpha decay results from Coulomb repulsion between alpha particle and the rest of the nucleus. Figure 1.10 shows alpha decay with two protons and two neutrons from a parent nucleus.
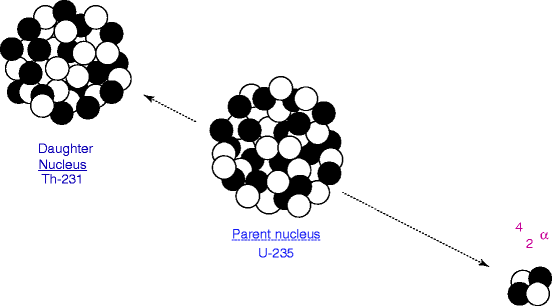

Fig. 1.10
Radiation of alpha particle
Heavy nuclei are energetically unstable against spontaneous emission of an alpha (α) particle (or 4He nucleus). The decay process proceeds as
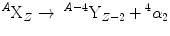
where X and Y are the initial and final nuclear species; A, the atomic number; and Z, the atomic weight. For each distinct transition between initial and final nucleus, a fixed energy difference (E b–E e, where E b is binding energy of the incident particle and E e is the binding energy of escaping—particles relative to the compound nucleus) or Q-value characterizes the decay.
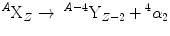
(1.16)
It has been found that there is a strong correlation between alpha (α) particle energy and half-life of the parent isotope and the particle with the shortest half-life has the highest energy. The most common calibration source of α-particle is americium-241 (241Am). Monoenergetic α-particle sources are prepared in very thin layers, because α-particle loses energy very rapidly in materials.
Alpha particles, like helium nuclei, have a net spin of zero and have a classical total energy of about 5 MeV. These particles are highly ionized and have low penetration depth. Currently alpha (α)-emitting radioisotopes are finding much interest in nuclear medicine for radiotherapy and imaging [42] (Table 1.5). Isotope emitting alpha particle causes more damage to the body cells compared to the other ionizing particles due to their high relative biological effectiveness.
Table 1.5
Alpha-emitting radioisotopes of current interest
Radioisotope | Energy of the emitting α-particle (MeV) | Half-life | Production method |
|---|---|---|---|
Terbium-149 (149Tb) | 3.9 | 4.1 h | Accelerator |
Astatine-211 (211At) | 6.8 | 7.2 h | Accelerator |
Bismuth-212 (212Bi) | 7.8 | 60.5 min | Decay of lead-212 (212Pb) |
Bismuth-213 (213Bi) | 5.8 | 45 min | Decay of actimium-225 (225Ac) |
The binding energy of α-particle is variable and can go from zero to as high as 28.3 MeV. This contrasts with the binding energy of helium-3 (3He) which is only 8.0 MeV. Because of its high mass and energy, it interacts with the matter very heavily, and thus it has the shortest range among the three main particles (α, β, and γ) which are of importance in the field of nuclear medicine.
Figure 1.11 shows the penetrating capabilities of different radiation sources. From Fig. 1.11, it is clear that γ-particle has the highest penetrating power. In order to prevent unwanted nuclear radiation, shielding materials are very frequently used [43].


Fig. 1.11
The penetrating capabilities of different radiation sources
Shielding materials that are frequently used to protect from nuclear radiation are lead (Pb), concrete, and steel [44, 45]. Lead has the highest atomic number (82) and has highest density (11.32 g/cm3) among the shielding materials that are frequently used. It is mostly used in the form of rectangular blocks in the construction of gamma-ray shielding. Solid-shaped lead cast can also be used as shielding material. However, these solid cast materials sometimes contain voids and are not suitable for shielding.
Ordinary lead normally contains significant amount of natural activity due to low-level contaminants. Therefore, lead is specially refined to use as shielding material. Even when it is refined, it shows detectable radioactivity due to impurities from natural fallout. Sometimes lead mixed with plastic or epoxy compositions is used as shielding material. The photoelectric absorption cross section predominates up to gamma-ray energies as high as 0.5 MeV.
Iron or steel shielding is also used when lead shielding alone becomes expensive. In such circumstances, lead with a steel outer lining is used. However, the density and atomic number of iron is lower than lead (Pb). As a result, to make steel or iron shielding as effective as lead, the thickness of the steel shielding is made several tens of centimeters thicker than lead.
Concrete is also used as a shielding material. Because of its low cost, outer lining of concrete with inner lining of lead or steel is used. A special formulation of the concrete known as barytes concrete is preferably used as the material is much more effective in gamma-ray shielding. Table 1.6 shows the absorption coefficients of the radiation sources used in nuclear medicine. The absorption coefficients of the radiated sources are calculated on the basis of 511-keV photons [46].
Table 1.6
Absorption coefficients of the radiation sources used in nuclear medicine
Shielding material | α (cm−1) | β (cm−1) | γ (cm−1) |
|---|---|---|---|
Lead | 1.7772 | −0.5228 | 0.5457 |
Concrete | 0.1539 | −0.1161 | 2.0752 |
Steel | 0.5704 | −0.3063 | 0.6326 |
1.5.2 Beta (β) Particles
β-particles are just high-energy electrons ejected from the nucleus. Because of its higher energy than the energy of alpha (α) particle, it penetrates more inside the body tissue compared to the equal mass of α-particle. Beta (β) emission is accompanied by the emission of electron antineutrino which shares the momentum and energy of the decay. The emission of the electron’s antiparticle, the positron, is also called beta decay. The β−-decay can be represented by
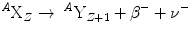
where X is the mother nucleus, Y is the final nucleus, and ν − is the antineutrino [47, 48]. The neutrinos and antineutrinos are extremely small, and their interaction probability with matter is undetectable. The recoil nucleus Y passes almost zero energy, and the total energy is shared between the beta (β) particle and the invisible neutrino with no mass and charge. The β-particle, on the other hand, changes its energy from decay to decay, which can range from zero to the end-point energy. A fixed decay energy or Q-value characterizes each specific β-decay.
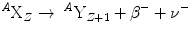
(1.17)
β-decay is relatively a slow process and may lead to population of the excited state in the daughter nucleus having a shorter average lifetime. The excited daughter nucleus can come down to the ground state (non-excited state) through the emission of gamma-ray (γ-ray) photon whose energy is essentially equal to the difference in energy between the initial and final nuclear states. The fact that β-decay involves emission of electrons, that is, particles constituting the atom, from the nucleus stems has been established from the following considerations:
(a)
The mass and charge of β−-particles are identical to those of atomic electrons.
(b)
β+-particles are annihilated by the atomic electrons.
(c)
Atomic electrons are captured by the nuclei.
(d)
Pauli’s exclusion principle is valid for mixed ensemble of particles contains atomic electrons and β−-particles.
Figure 1.12 shows the decay of cobalt-60 (60Co27) to nickel-60 (60Ni28). Another example of gamma (γ)-ray radiation is the formation of neptunium-237 (237Np) from americium-241 (241Am) during α-decay. In some cases, the γ-emission spectrum is simple, for example, 60Co/60Ni. But in 241Am/237Np and 192Ir/192Pt, the γ-emission spectra are complex, and they reveal the existence of a series of nuclear energy levels. The fact that an α-spectrum can have a series of different peaks with different energies reinforces the idea that several nuclear energy levels are possible. But it is completely different when γ-ray is accompanied by β-particle emission [49, 50]. It has been found that the β-spectrum never shows a sharp peak, because a β-decay is accompanied by the emission of a neutrino, which carries away the energy (Fig. 1.13) [51, 52]. The transmission curve for β-particles emitted by a radioisotope differs significantly because of continuous distribution of their energies.
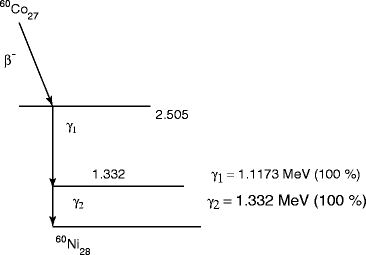
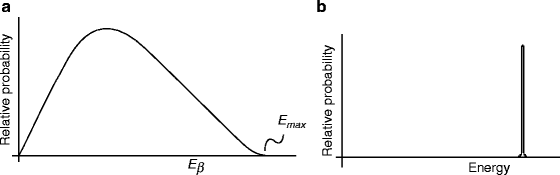

Fig. 1.12
Decay of cobalt-60 (60Co27)

Fig. 1.13
(a) The peak of an alpha spectrum and (b) beta spectrum without a sharp peak
The absorption coefficient (α) of a specific absorber is defined as
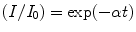 or
or
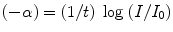
where I is the initial counting rate, I 0 the final counting rates with absorber, and t the thickness of the absorber in g/cm2. It has been found that the value of α correlates very well with the end-point energy of the β-emitter for a specific absorber. The energy deposited within the absorber can be represented mathematically by
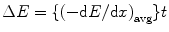
where (−dE/dx) is the linear stopping power averaged over the energy of the particle and t is the thickness of the absorber. If the energy loss within the absorber is small, the stopping power does not change much; otherwise, it is difficult to obtain a properly weighted (−dE/dx)avg value directly from the data. On the other hand, the stopping time (t stop) required to stop the charged particles within an absorber can be written as
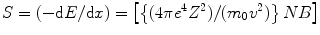
where Z is the atomic number, N the density of the absorber, e the electronic charge, m 0 the rest mass, and B = Z{ln (2m 0 v 2/I)– ln (1 − v 2/c 2) − (v 2/c 2)}, where I is the average excitation and ionization potential of the absorber. The expression for B shows that it varies slowly with particle energy.
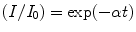
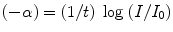
(1.18)
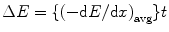
(1.19)
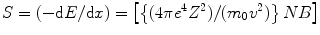
(1.21)
1.5.3 Gamma (γ) Rays
Gamma (γ) ray is a short wavelength electromagnetic radiation of nuclear origin, having energy varying from 10 keV to 5 MeV. It is the spontaneous emission of gamma (γ) quanta by the nucleus and was discovered by a French chemist and physicist, Paul Ulrich Villard, in 1900. The γ-quanta emitted by the nucleus during transition to a lower energy state may carry different angular momenta.
The γ-rays are the highest range of energetic form of electromagnetic radiation and are more energetic than alpha (α) and beta (β) radiation but less than the energy possessed by an ionizing radiation. They damage the body tissues and skin, similar to that caused by X-rays, such as burns, cancer, and genetic mutation. Gamma rays are produced by the nuclear transitions, while X-rays are produced by energy transitions due to accelerating electrons. Both of these rays are used in nuclear medicine for diagnosis and therapy of the abnormal cells.
The major interactions of γ rays with matter that play an important role in the measurements of radiation are photoelectric effect, Compton effect, and pair production. Photoelectric effect is due to the low-energy interactions of γ-rays with the absorber material of high atomic number (Z). The photoelectric effect is the dominant energy transfer mechanism for X-rays and γ-rays with photon energies below 50 keV.
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree