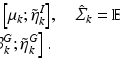Fig. 1.
Illustration of the proposed method. The atlas space is first defined using images of the first time frame (TF). All the time sequences are transformed into the atlas space and the initial spatio-temporal atlas is constructed at each time frame independently. To circumvent the temporal mismatch as shown in TF 10 of subject N, we regroup each time frame based on the Lipschitz norm on diffeomorphisms between each subject and the initial atlas. For example, TF 10 of subject N is included at TF 11 in the final atlas construction. Note that the different widths of the line represent the variations in tongue shape over time.
Recent advances in tongue imaging methods such as magnetic resonance imaging (MRI) have accelerated new advances in image and motion analysis, including segmentation [1, 2], motion tracking [3], motion clustering [4], and registration [5, 6]. However, despite the popularity of an atlas in other organs (e.g., the brain [7, 8] or the heart [9]), research on the tongue or vocal tract atlas is still in its infancy; recently the first vocal tract atlas and statistical model have been published in [10], where structural MRI from normal subjects were used to build the atlas. However, to the best of our knowledge, there has been no spatio-temporal atlas of the tongue during speech or swallowing to date.
In order to create such a spatio-temporal atlas, finding accurate mappings of subjects of a population into a common space is essential. In particular, it is of critical importance to encode both intra-subject motion characteristics and inter-subject difference in the constructed spatio-temporal atlas. Several attempts have been made to address this for the brain and the cardiac applications by performing groupwise registration with kernel regression [8, 11] or with an individual subject’s growth model [12] or by aligning jointly subject image sequences to a template sequence [13]. In the similar context, Lorenzi et al. [14] presented the Schild’s Ladder framework to transport longitudinal deformations in time series of images in a common space using diffeomorphic registration.
In this work, motivated by the works above, we propose to construct an unbiased spatio-temporal atlas of the tongue for the first time to characterize the dynamic tongue motion changes given a specific speech task, based on cine-MRI from eighteen normal speakers. In contrast to the other works above, changes in tongue motion and anatomy are much more variable and complex. Therefore, we develop a framework based on diffeomorphic registration that can capture large and complex deformations in its spatial and temporal tongue shape changes while maintaining topological properties of the tongue. In addition, in our application, the number of time frames for each subject is the same but each time sequence may not be accurately aligned temporally as shown in Fig. 1 (see time frame 10). To address this, the proposed framework consists of multiple steps, which formulates both spatial and temporal alignment problems independently. We attempted to find the minimum distance on diffeomorphisms and proposed an algorithm to solve this problem using the atlas of the reference time frame and the Lipschitz norm on diffeomorphisms, respectively. We evaluated and compared the different configurations such as the similarity measure to build the atlas. We will detail each step and the evaluation in the following sections.
2 Materials and Methods
2.1 Data Acquisition
MRI Instrumentation and Data Collection. In our study, MRI scanning was performed on a Siemens 3.0 T Trim Treo system (Siemens Medical Solutions, Malvern, PA) with a 16-channel head and neck coil. When the subject speaks a pre-trained speech task in repeated utterances, cine MR images were acquired as a sequence of image frames at multiple parallel slice locations that cover a region of interest encompassing the tongue and the surrounding structures. To optimize the spatial resolution in all three planes, the three orthogonal stacks including axial, coronal, and sagittal orientations were acquired. Each dataset had a 1 s duration, 26 time frames per second, 6 mm slice thickness and 1.8 mm in-plane resolution. Other sequence parameters were repetition time (TR) 36 ms, echo time (TE) 1.47 ms, flip angle 6 , and turbo factor 11.
, and turbo factor 11.
 , and turbo factor 11.
, and turbo factor 11.Speech Task. The MRI speech task was “a geese”. This phrase begins with a neutral vocal tract configuration (schwa). The tongue body motion is simple because it moves only anteriorly, and the word uses little to no jaw motion, thus increasing the potential for tongue deformation. There are four distinctive frames /ə/, /g/, /i/, and /s/ in this word.
2.2 Preliminaries
Preprocessing. Our study uses T2-weighted multi-slice 2D dynamic cine-MRI at a frame rate of 26 frames per second. To maintain high signal-to-noise ratio (SNR) while minimizing the blurred effect due to involuntary motion such as swallowing, three orthogonal volumes with axial, sagittal, and coronal orientations are acquired one after the other. Each orientation, however, cannot be used directly for further atlas construction. In order to create a single volume with an isotropic resolution, a super-resolution volume reconstruction technique using all three stacks is employed [2, 15]. In brief, multiple preprocessing tasks including motion correction, intensity normalization, etc. are carried out, which precedes a region-based Maximum A Posteriori-Markov Random Field (MAP-MRF) method incorporating edge-preserving regularization to reconstruct a single volume termed a super-volume with improved SNR and resolution (1.8 mm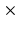 1.8 mm
1.8 mm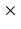 1.8 mm).
1.8 mm).
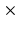 1.8 mm
1.8 mm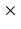 1.8 mm).
1.8 mm).Diffeomorphic Image Registration. Diffeomorphic image registration is the key technique to construct the atlas. In particular, we are interested in the well-known Large Deformation Diffeomorphic Metric Mapping (LDDMM) algorithm [16]. The ANTs open source software library [17] is used in our implementation. Let the images 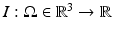 and
and 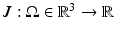 , defined on the open and bounded domain
, defined on the open and bounded domain 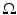 , be the template and target images. We cast image registration as the problem of finding a diffeomorphic transformation,
, be the template and target images. We cast image registration as the problem of finding a diffeomorphic transformation, 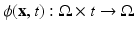 , parameterized over time, which is a differentiable mapping with a differentiable inverse. The
, parameterized over time, which is a differentiable mapping with a differentiable inverse. The 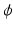 can be computed by integrating a time-dependent velocity field
can be computed by integrating a time-dependent velocity field 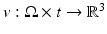 , as given by
, as given by
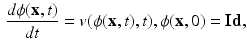
where the diffeomorphic mapping can be obtained through integration of Eq. (1):
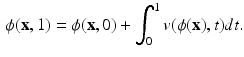
The diffeomorphic, inexact image matching energy functional in a variational framework can be given by
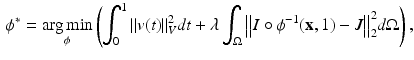
where the energy functional consists of the regularization term (the first term on the right), the data fidelity term or similarity measure (the second term on the right), V is a Reproducing Kernel Hilbert Space (RKHS) of vector fields on the domain 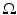 , and
, and 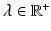 is a balancing term. In recent years, new improvements have been made in the original LDDMM formulation [16]. The first is the generalization of the similarity measures to include mutual information (MI) or cross correlation (CC) in order to accommodate intensity differences [7]. The second is the use of a symmetric alternative, utilizing the fact that the diffeomorphism,
is a balancing term. In recent years, new improvements have been made in the original LDDMM formulation [16]. The first is the generalization of the similarity measures to include mutual information (MI) or cross correlation (CC) in order to accommodate intensity differences [7]. The second is the use of a symmetric alternative, utilizing the fact that the diffeomorphism, 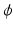 , can be decomposed into a pair of diffeormorphisms
, can be decomposed into a pair of diffeormorphisms 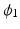 and
and 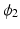 [7]. The formulation incorporating the two new features is
[7]. The formulation incorporating the two new features is
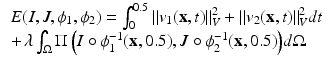
where 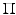 denotes a similarity measure depending on the considered application. In this work, we use the CC as our similarity metric. The optimal
denotes a similarity measure depending on the considered application. In this work, we use the CC as our similarity metric. The optimal 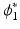 and
and 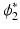 can be obtained via minimizing the energy functional from t = 0 and t = 1, respectively, thus leading to a symmetric and inverse consistent mapping.
can be obtained via minimizing the energy functional from t = 0 and t = 1, respectively, thus leading to a symmetric and inverse consistent mapping.
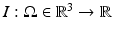 and
and 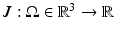 , defined on the open and bounded domain
, defined on the open and bounded domain 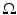 , be the template and target images. We cast image registration as the problem of finding a diffeomorphic transformation,
, be the template and target images. We cast image registration as the problem of finding a diffeomorphic transformation, 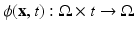 , parameterized over time, which is a differentiable mapping with a differentiable inverse. The
, parameterized over time, which is a differentiable mapping with a differentiable inverse. The 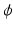 can be computed by integrating a time-dependent velocity field
can be computed by integrating a time-dependent velocity field 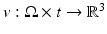 , as given by
, as given by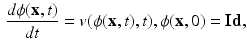
(1)
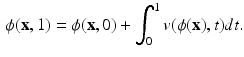
(2)
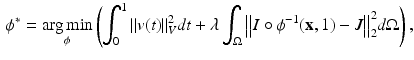
(3)
 , and
, and 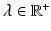 is a balancing term. In recent years, new improvements have been made in the original LDDMM formulation [16]. The first is the generalization of the similarity measures to include mutual information (MI) or cross correlation (CC) in order to accommodate intensity differences [7]. The second is the use of a symmetric alternative, utilizing the fact that the diffeomorphism,
is a balancing term. In recent years, new improvements have been made in the original LDDMM formulation [16]. The first is the generalization of the similarity measures to include mutual information (MI) or cross correlation (CC) in order to accommodate intensity differences [7]. The second is the use of a symmetric alternative, utilizing the fact that the diffeomorphism, 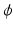 , can be decomposed into a pair of diffeormorphisms
, can be decomposed into a pair of diffeormorphisms 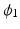 and
and 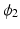 [7]. The formulation incorporating the two new features is
[7]. The formulation incorporating the two new features is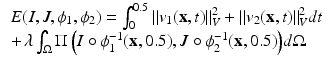
(4)
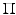 denotes a similarity measure depending on the considered application. In this work, we use the CC as our similarity metric. The optimal
denotes a similarity measure depending on the considered application. In this work, we use the CC as our similarity metric. The optimal 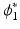 and
and 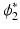 can be obtained via minimizing the energy functional from t = 0 and t = 1, respectively, thus leading to a symmetric and inverse consistent mapping.
can be obtained via minimizing the energy functional from t = 0 and t = 1, respectively, thus leading to a symmetric and inverse consistent mapping.Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree