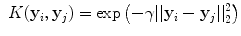. The energy function of the CRF defines a posterior probability distribution 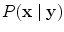 for a set of class labels
for a set of class labels 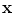 for the superpixels, given a set of features
for the superpixels, given a set of features 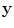 describing the superpixels. The energy function can be written as a sum of first- and second-order potential functions in the form
describing the superpixels. The energy function can be written as a sum of first- and second-order potential functions in the form
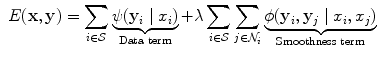
(1)
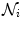 is the set of neighbours of superpixel
is the set of neighbours of superpixel 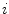 . The constant
. The constant 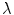 controls the relative importance of the data and smoothness terms. The CRF formulation enables maximum a posteriori (MAP) inference of the labels
controls the relative importance of the data and smoothness terms. The CRF formulation enables maximum a posteriori (MAP) inference of the labels 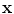 to be carried out efficiently using graph cuts. We use the min-cut/max-flow algorithm of [4] to find the optimal solution.
to be carried out efficiently using graph cuts. We use the min-cut/max-flow algorithm of [4] to find the optimal solution.We define the potential functions of (1) by using supervised learning on labelled superpixel features and deriving constraints using the resulting trained models. Sections 3 and 4 describe the superpixel features used to learn the constraints and how they are incorporated into the CRF potential functions.
3 Superpixels
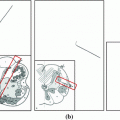
We use the Simple Linear Iterative Clustering (SLIC) [1, 16] algorithm to partition the image into superpixels. As shown in Fig. 1, boundaries of superpixels tend to coincide with boundaries of anatomical objects, enabling an accurate pixel-level segmentation to be recovered from the classified superpixels. The primary advantages of using superpixels are twofold: firstly, as the number of nodes in the graph decreases significantly from a pixel-level graph, there is a corresponding reduction in computational complexity. Secondly, multiple features can be extracted from the superpixel regions which can help to discriminate between the classes more effectively.
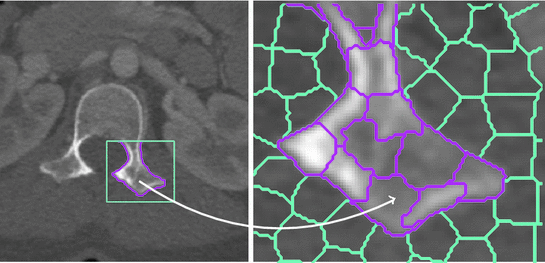

Fig. 1
The left figure shows a CT slice with ground truth contour (magenta) for a section of the vertebra. The right figure shows boundaries for superpixels assigned to the vertebra class (magenta) and background class (cyan). The superpixels preserve the boundary detail of the vertebrae (color figure online)
We aim to characterise the superpixels by extracting multiple features from them that incorporate information about intensity, texture, location and edge response. As described in the next section, these features are used to discriminate between the vertebra and background superpixels by learning a classifier and distance metric on a set of ground truth images. We emphasise that this training occurs only once, after which the trained models can be used in the CRF potential functions for any further images.
The superpixel features are summarised in Table 1. The feature vector for a superpixel 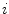 is a concatenation of the individual features:
is a concatenation of the individual features:
![$$\begin{aligned} \begin{aligned} \mathbf {y}_i = [\mathbf {y}_i^T, \mathbf {y}_i^L, \mathbf {y}_i^E]^{\top }. \end{aligned} \end{aligned}$$](/wp-content/uploads/2016/10/A331518_1_En_6_Chapter_Equ2.gif)
We exhaustively tested different subsets of the features, but found that the best performance was obtained by combining all features. The features were chosen in part for their generality and as a consequence are directly applicable to different imaging modalities such as MRI [9].
 is a concatenation of the individual features:
is a concatenation of the individual features:Table 1
Superpixel features (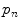 denotes the
denotes the 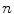 th percentile)
th percentile)
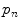 denotes the
denotes the 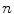 th percentile)
th percentile)Feature | Description | Dimension |
|---|---|---|
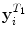 | Concatenation of intensity histogram from superpixel 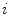 and average histogram from neighbours and average histogram from neighbours 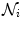 | 20 |
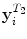 | SIFT descriptor calculated at the centroid of superpixel 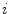 | 128 |
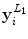 | Mean, 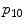 and and 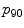 of the row and column pixel coordinates in the superpixel, centred on the matched contour region of the row and column pixel coordinates in the superpixel, centred on the matched contour region | 6 |
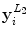 | Mean, 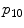 and and 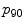 of the matched contour distance transform gradient in the superpixel, in both the horizontal and vertical direction of the matched contour distance transform gradient in the superpixel, in both the horizontal and vertical direction | 6 |
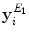 | Mean, 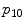 and and 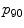 of the LoG response within the superpixel, taken over 4 scales of the LoG response within the superpixel, taken over 4 scales | 12 |
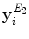 | Mean, 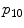 and and 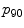 of the structure tensor eigenvalues of the superpixel, taken over 4 scales of the structure tensor eigenvalues of the superpixel, taken over 4 scales | 24 |
![$$\begin{aligned} \begin{aligned} \mathbf {y}_i = [\mathbf {y}_i^T, \mathbf {y}_i^L, \mathbf {y}_i^E]^{\top }. \end{aligned} \end{aligned}$$](/wp-content/uploads/2016/10/A331518_1_En_6_Chapter_Equ2.gif)
(2)
The first set of features 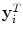 characterise the intensity and textural properties of the superpixels. They take the form of normalised intensity histograms over the pixels within each superpixel and SIFT [14, 16] descriptors of a fixed size calculated at the superpixel centroids.
characterise the intensity and textural properties of the superpixels. They take the form of normalised intensity histograms over the pixels within each superpixel and SIFT [14, 16] descriptors of a fixed size calculated at the superpixel centroids.
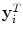 characterise the intensity and textural properties of the superpixels. They take the form of normalised intensity histograms over the pixels within each superpixel and SIFT [14, 16] descriptors of a fixed size calculated at the superpixel centroids.
characterise the intensity and textural properties of the superpixels. They take the form of normalised intensity histograms over the pixels within each superpixel and SIFT [14, 16] descriptors of a fixed size calculated at the superpixel centroids.The location features are based on a local coordinate system for each vertebra. This helps segmentation by providing features that describe the superpixel’s relative location. The local coordinates are obtained by matching a contour to the top of the vertebral body. We do this by first (automatically) cropping the ground truth segmentation contours above their centroids, so that the resulting contour set  corresponds to the upper, roughly semi-circular, boundary of each vertebral body in the ground truth set. Each ground truth image is therefore associated with a single contour
corresponds to the upper, roughly semi-circular, boundary of each vertebral body in the ground truth set. Each ground truth image is therefore associated with a single contour  and our goal is to find the best matching contour of the set for a new image. We use a Laplacian of Gaussian (LoG) filter to detect the outer boundary of the vertebra and search over the image to find the point where the average LoG response along the contour is greatest. The best match is the contour with the maximum response of the set. Features are derived from the matched contour region by centring the pixel coordinates at the region’s centroid and computing the gradient of the distance transform [9]. While the matching process depends on the presence of an adequate number of ground truth contours, in practice only an approximate match to the vertebra is required to derive the location features. Using a set of generated synthetic contours is a possibility in cases where the ground truth data is very limited.
and our goal is to find the best matching contour of the set for a new image. We use a Laplacian of Gaussian (LoG) filter to detect the outer boundary of the vertebra and search over the image to find the point where the average LoG response along the contour is greatest. The best match is the contour with the maximum response of the set. Features are derived from the matched contour region by centring the pixel coordinates at the region’s centroid and computing the gradient of the distance transform [9]. While the matching process depends on the presence of an adequate number of ground truth contours, in practice only an approximate match to the vertebra is required to derive the location features. Using a set of generated synthetic contours is a possibility in cases where the ground truth data is very limited.
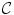 corresponds to the upper, roughly semi-circular, boundary of each vertebral body in the ground truth set. Each ground truth image is therefore associated with a single contour
corresponds to the upper, roughly semi-circular, boundary of each vertebral body in the ground truth set. Each ground truth image is therefore associated with a single contour 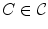 and our goal is to find the best matching contour of the set for a new image. We use a Laplacian of Gaussian (LoG) filter to detect the outer boundary of the vertebra and search over the image to find the point where the average LoG response along the contour is greatest. The best match is the contour with the maximum response of the set. Features are derived from the matched contour region by centring the pixel coordinates at the region’s centroid and computing the gradient of the distance transform [9]. While the matching process depends on the presence of an adequate number of ground truth contours, in practice only an approximate match to the vertebra is required to derive the location features. Using a set of generated synthetic contours is a possibility in cases where the ground truth data is very limited.
and our goal is to find the best matching contour of the set for a new image. We use a Laplacian of Gaussian (LoG) filter to detect the outer boundary of the vertebra and search over the image to find the point where the average LoG response along the contour is greatest. The best match is the contour with the maximum response of the set. Features are derived from the matched contour region by centring the pixel coordinates at the region’s centroid and computing the gradient of the distance transform [9]. While the matching process depends on the presence of an adequate number of ground truth contours, in practice only an approximate match to the vertebra is required to derive the location features. Using a set of generated synthetic contours is a possibility in cases where the ground truth data is very limited.Finally, the features in 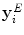 are distinctive of superpixels at the edges and corners of the vertebrae and help to separate the vertebra and background classes around the boundary. We take the LoG response within the superpixel over 4 different scales to form the first feature vector. The second feature vector is formed from the eigenvalues of the structure tensor [12] within the superpixel, taken over 4 scales.
are distinctive of superpixels at the edges and corners of the vertebrae and help to separate the vertebra and background classes around the boundary. We take the LoG response within the superpixel over 4 different scales to form the first feature vector. The second feature vector is formed from the eigenvalues of the structure tensor [12] within the superpixel, taken over 4 scales.
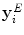 are distinctive of superpixels at the edges and corners of the vertebrae and help to separate the vertebra and background classes around the boundary. We take the LoG response within the superpixel over 4 different scales to form the first feature vector. The second feature vector is formed from the eigenvalues of the structure tensor [12] within the superpixel, taken over 4 scales.
are distinctive of superpixels at the edges and corners of the vertebrae and help to separate the vertebra and background classes around the boundary. We take the LoG response within the superpixel over 4 different scales to form the first feature vector. The second feature vector is formed from the eigenvalues of the structure tensor [12] within the superpixel, taken over 4 scales.4 Potential Functions
We next describe the potential functions used in (1). Both the data and smoothness terms of the CRF are based on the characteristics learned from superpixel training examples.
We first convert the pixel-level ground truth labels into superpixel-level labels by assigning each superpixel to the class with the majority vote; as Fig. 1 illustrates, there is little ambiguity in this assignment. We then use the superpixel feature/label examples to train a support vector machine (SVM) [5] using an RBF kernel, given by