vertebrae (T4-L5) from one normal and one scoliotic magnetic resonance (MR) spine image using six manual and two computerized measurements. Manual measurements were performed by superior and inferior tangents, anterior and posterior tangents, and mid-endplate and mid-wall lines. Computerized measurements were performed by automatically evaluating the symmetry of vertebral anatomy in sagittal cross-sections and volumetric images. The mid-wall lines were the manual measurements with the lowest intra- and inter-observer variability (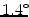 and
and 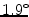 standard deviation, SD). The strongest inter-method agreement was found between the mid-wall lines and posterior tangents (
standard deviation, SD). The strongest inter-method agreement was found between the mid-wall lines and posterior tangents (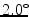 SD). Computerized measurements did not yield intra- and inter-observer variability (
SD). Computerized measurements did not yield intra- and inter-observer variability (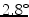 and
and 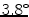 SD) as low as the mid-wall lines, but were still comparable to the intra- and inter-observer variability of the superior (
SD) as low as the mid-wall lines, but were still comparable to the intra- and inter-observer variability of the superior (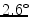 and
and 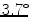 SD) and inferior (
SD) and inferior (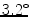 and
and 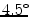 SD) tangents.
SD) tangents.
1 Introduction
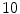 radiographs of L4/L5 and L5/S1 segments. The manual and computer-assisted measurements proved to be equivalent in terms of variability, the Cobb angle and posterior tangents were the least variable, and the anterior tangents were the most reliable measurements. Street et al. [15] evaluated the reliability of measuring kyphosis manually from different imaging modalities in the case of thoracolumbar fractures. For the Cobb angle measurements, they concluded that plain radiographs were the most reliable measurement modality, followed by computed tomography (CT) and finally by magnetic resonance (MR) imaging.
radiographs of L4/L5 and L5/S1 segments. The manual and computer-assisted measurements proved to be equivalent in terms of variability, the Cobb angle and posterior tangents were the least variable, and the anterior tangents were the most reliable measurements. Street et al. [15] evaluated the reliability of measuring kyphosis manually from different imaging modalities in the case of thoracolumbar fractures. For the Cobb angle measurements, they concluded that plain radiographs were the most reliable measurement modality, followed by computed tomography (CT) and finally by magnetic resonance (MR) imaging.2 Methodology
2.1 Manual Measurements
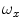 of SVI, measured against reference horizontal or vertical lines that are parallel to the coordinate system of the 3D image.
of SVI, measured against reference horizontal or vertical lines that are parallel to the coordinate system of the 3D image.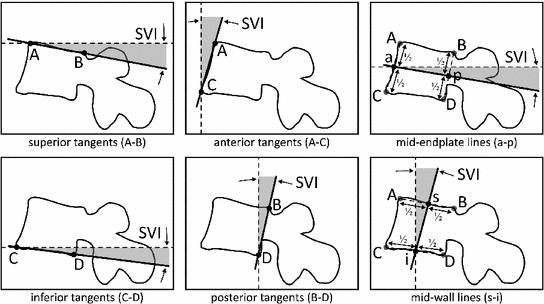
2.2 Computerized Measurements
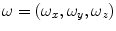 of rotation of the local vertebral coordinate system
of rotation of the local vertebral coordinate system  (defined by Cartesian unit vectors
(defined by Cartesian unit vectors 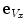 ,
, 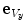 and
and 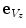 ) around the axes of the global image coordinate system
) around the axes of the global image coordinate system 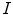 (defined by Cartesian unit vectors
(defined by Cartesian unit vectors 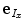 ,
, 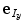 and
and 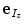 ). Both
). Both 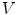 and
and 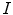 are right-hand Cartesian coordinate systems, representing left-to-right (
are right-hand Cartesian coordinate systems, representing left-to-right (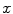 -axis), anterior-to-posterior (
-axis), anterior-to-posterior (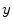 -axis) and cranial-to-caudal (
-axis) and cranial-to-caudal (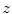 -axis) direction. The angles
-axis) direction. The angles 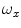 (i.e. SVI),
(i.e. SVI), 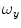 (i.e. coronal vertebral inclination) and
(i.e. coronal vertebral inclination) and 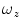 (i.e. axial vertebral rotation) then represent the rotation of the vertebral coordinate system
(i.e. axial vertebral rotation) then represent the rotation of the vertebral coordinate system 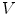 around vectors
around vectors 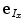 (pitch),
(pitch), 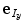 (roll) and
(roll) and 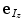 (yaw), respectively. If the origin of
(yaw), respectively. If the origin of 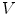 is located at the vertebral centroid and
is located at the vertebral centroid and 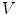 is rotationally aligned with the vertebra in
is rotationally aligned with the vertebra in 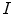 , anatomically corresponding symmetrical parts of the vertebra can be observed within volumes of interest (VOIs) along positive/negative directions of each axis
, anatomically corresponding symmetrical parts of the vertebra can be observed within volumes of interest (VOIs) along positive/negative directions of each axis 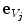 ,
, 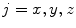 . The angles
. The angles 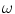 of vertebral rotation can be therefore determined by finding the planes of maximal symmetry, which divide the whole vertebra into symmetrical left/right (
of vertebral rotation can be therefore determined by finding the planes of maximal symmetry, which divide the whole vertebra into symmetrical left/right (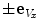 ) halves, and the vertebral body into symmetrical anterior/posterior (
) halves, and the vertebral body into symmetrical anterior/posterior (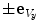 ) and cranial/caudal (
) and cranial/caudal (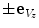 ) halves. For each axis
) halves. For each axis 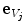 ,
, 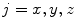 , the symmetrical correspondences of the two halves (
, the symmetrical correspondences of the two halves (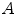 and
and 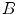 ) of a VOI are measured by
) of a VOI are measured by 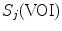 :
: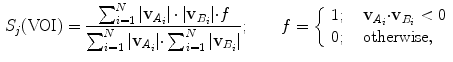
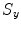 ), shown for a symmetrical pair of points
), shown for a symmetrical pair of points 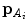 and
and 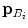 inside
inside 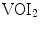 . b The vertebral coordinate system
. b The vertebral coordinate system 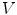 and the observed volumes of interest (
and the observed volumes of interest (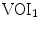 encompasses the whole vertebra,
encompasses the whole vertebra, 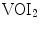 encompasses the vertebral body)
encompasses the vertebral body)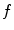 is the weighting function, and
is the weighting function, and 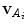 and
and 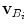 are the projections of the intensity gradient vectors
are the projections of the intensity gradient vectors 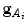 and
and 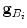 in the coordinate system
in the coordinate system 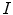 to the unit vector
to the unit vector 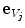 ,
, 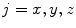 , of the coordinate system
, of the coordinate system 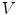 at symmetrical pair of points
at symmetrical pair of points 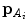 and
and 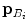 , respectively, and
, respectively, and 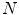 is the number of point pairs inside each VOI (Fig. 2a). By projecting the gradient vectors to
is the number of point pairs inside each VOI (Fig. 2a). By projecting the gradient vectors to 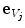 ,
, 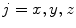 , and by applying the weighting function
, and by applying the weighting function 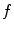 , we retain the gradient components
, we retain the gradient components 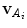 and
and 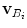 that are relevant for defining the vertebral symmetry in the direction of
that are relevant for defining the vertebral symmetry in the direction of 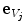 . Two variations of the computerized method were applied for each vertebra. The measurements in 3D automatically evaluated the vertebral rotation in 3D images by maximizing symmetrical correspondences:
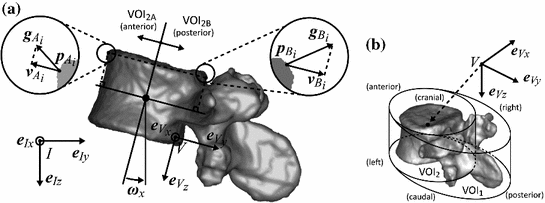
. Two variations of the computerized method were applied for each vertebra. The measurements in 3D automatically evaluated the vertebral rotation in 3D images by maximizing symmetrical correspondences: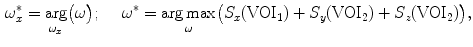
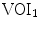 , and the VOI that encompasses the vertebral body is denoted by
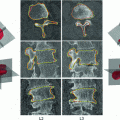
, and the VOI that encompasses the vertebral body is denoted by 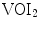 (Fig. 2b). On the other hand, the measurements in 2D automatically evaluated SVI in the same 2D oblique sagittal cross-sections that were used for manual measurements (Fig. 3) by considering only
(Fig. 2b). On the other hand, the measurements in 2D automatically evaluated SVI in the same 2D oblique sagittal cross-sections that were used for manual measurements (Fig. 3) by considering only 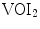 that encompasses the vertebral body and reducing its dimensionality to the area of interest (AOI), and maximizing the remaining symmetrical correspondences:
that encompasses the vertebral body and reducing its dimensionality to the area of interest (AOI), and maximizing the remaining symmetrical correspondences: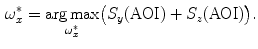
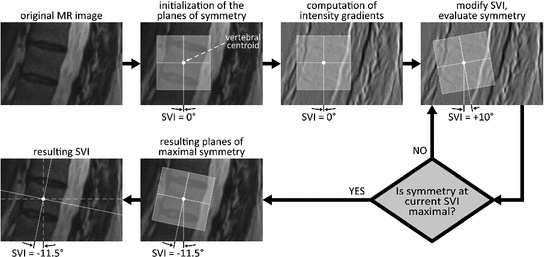
 mm in size to encompass the whole vertebral body of thoracic and lumbar segments. By rotating these planes in 3D, the rotation angles
mm in size to encompass the whole vertebral body of thoracic and lumbar segments. By rotating these planes in 3D, the rotation angles 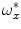 are obtained from the inclination of the planes, and the current symmetrical correspondences are evaluated by mirroring the edges of vertebral anatomical structures (obtained from image intensity gradients) over each plane and comparing them to the edges on the opposite side of that plane in an optimization procedure.
are obtained from the inclination of the planes, and the current symmetrical correspondences are evaluated by mirroring the edges of vertebral anatomical structures (obtained from image intensity gradients) over each plane and comparing them to the edges on the opposite side of that plane in an optimization procedure.3 Experiments and Results
3.1 Images and Observers
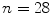 vertebrae between segments T4 and L5 from one normal (
vertebrae between segments T4 and L5 from one normal (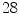 -year male,
-year male,  frontal Cobb angle) and one scoliotic (
frontal Cobb angle) and one scoliotic (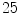 -year male,
-year male, 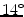 frontal Cobb angle) spine image were included in this study. The T2-weighted MR scans (mean repetition and echo time TR
frontal Cobb angle) spine image were included in this study. The T2-weighted MR scans (mean repetition and echo time TR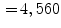
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree