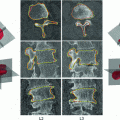
) was observed in comparison to a previous approach. An automatic classification based on torsion indices identified two groups: one with high torsion values (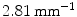 ) and one with low torsion values (
) and one with low torsion values (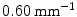 ), showing the existence of two sub-groups of 3D deformations stemming from the same 2Dclass.
), showing the existence of two sub-groups of 3D deformations stemming from the same 2Dclass.
Supported by the CHU Sainte-Justine Academic Research Chair in Spinal Deformities, the Canada Research Chair in Medical Imaging and Assisted Interventions and the 3D committee of the Scoliosis Research Society.
1 Introduction
Spinal deformity pathologies such as adolescent idiopathic scoliosis (AIS) are complex three-dimensional (3D) deformations of the trunk, described as a lateral deviation of the spine combined with asymmetric deformation of the vertebrae. Surgical treatment usually involves correction of the scoliotic curves with preshaped metal rods anchored in the vertebrae with screws and arthrodesis (bone fusion) of the intervertebral articulations. The most widely used classification paradigms for scoliosis are two-dimensional (2D) since they are based on spine X-rays in the sagittal and coronal planes. The Lenke classification [1] is one of the most accepted and widely used classification systems for AIS because it is easy to use and provides treatment recommendations. It offers a global evaluation of the scoliotic spine and offers better inter- as well as intra-observer reliability to previous systems [1–3]. However, it is still a 2D assessment of scoliosis that is based on the structurality and magnitude of Cobb angles in the proximal thoracic (PT), main thoracic (MT) as well as thoracolumbar/lumbar (TL/L) regions. Since 2D measurements and classification systems do not completely describe this 3D deformity, response to treatment for scoliosis can be at times difficult to accurately predict [4]. This is because 2D measurements are often measured on a plane of view that does not capture the position and orientation of the scoliosis curve in space. Consequently, two different scoliosis deformities may have similar 2D measurements. Applying similar treatments strategies based on similar 2D measurements may thus yield different surgical outcomes. Hence, there is a growing need to study scoliosis in 3D and develop 3D descriptors that will better characterize scoliosis and improve patient care.
Due to the 3D nature of AIS, the natural curvature properties of the spinal curve were also exploited with the goal of defining better indices to characterize the third dimension of scoliosis. Stokes et al. first introduced axial rotation (AR) as a local measure evaluated in the transverse plane to assess the effect of derotation maneuvers in surgical procedures [5]. Understanding how to classify and quantify 3D spinal deformities remains a difficult challenge in scoliosis. Recently, the Scoliosis Research Society (SRS) has recognized the need for 3D classification and mandated the 3D Scoliosis Committee to continue their efforts towards developing a 3D scheme for characterizing scoliosis. Duong et al. proposed an unsupervised fuzzy clustering technique in order to classify the 3D spine based on global shape descriptors [6]. Sangole et al. investigated the presence of subgroups within Lenke type-1 curves from 3D reconstructions of the spine, and proposed a new means to report 3D spinal deformities based on planes of maximal curvature (PMC) [7]. Recently, a multivariate analysis using manifold learning was able to identify four separate groups from the same cohort of thoracic deformities [8]. While these studies were able to identify different clusters of deformation using a series of 3D parameters, they were primarily qualitative and did not provide any quantifiable 3D measure to assess the severity of the deformation.
By using curved 3D line that passes through the thoracic and lumbar vertebra centroids to describe the general shape in the spine, several attempts have been made to measure the geometric torsion of the scoliotic curve. Geometric torsion is a property of a helicoidal line without specific relation to the rotation and deformation of the vertebrae themselve. Previous models demonstrated several limitations such as curve discontinuity caused by sequential modeling of the thoracic and lumbar segments or the inability to fit all types of scoliotic shapes. Therefore, geometric torsion was seldomly used as a reliable 3D geometric descriptor of scoliosis. To overcome this drawback, an approach was developed by Poncet et al. [9] to eliminate non-representative torsion spikes while minimizing the original geometric model deformity. This method was used to determine the amount of deviation (divergence) of the curved line from the plane determined by the tangent and normal vectors. These were then used to determine patterns of deformation based on torsion profiles. While the concept of scoliosis deformity was simplified using geometrical torsion by proposing a series of classification patterns, the method presented by Poncet et al. showed some limitations with respect to high sensitivity of inaccuracies in the 3D reconstruction, affecting the interpolated curvilinear shape of the spine. Furthermore, this measurement can only provide a local index at the vertebral level without a global measurement for an entire spinal segment. To circumvent these limitations, an alternative scheme for estimating curvature and torsion of planar and spatial curves was proposed, based on weighted least-square fitting and local arc-length approximation [10]. The method is simple enough to admit a convergence analysis that takes into account the effect of noise or inaccuracies in the 3D modeling of the spine.
In this paper, we propose a framework that infers the true 3D torsion parameter in AIS from biplanar X-rays images and automatically classifies patients in appropriate 3D sub-groups based on their torsion values. The general approach is described as follows. We first use a personalized 3D spine shape reconstructed from biplanar X-rays to obtain a landmark-based representation of the patient’s thoracic and lumbar spine. The spine is divided into three anatomical regions based on the spinal curve’s second derivatives. Geometric torsion measuring the twisting effect of the spine is then estimated at the junction of the segmental curves, using a novel technique by approximating local arc-lengths at the neutral vertebra in the thoracolumbar/lumbar segment. The torsion indices are then sent to a c-means classifier to identify the correct 3D sub-group. One of the applications is to help surgeons treat complicated deformity cases by offering a reliable predictor of the 3D deformation from the preoperative models and adapt the surgical strategy based on the defamation class. Section 2 presents the method in terms of geometric modeling and torsion estimator. Experiments are showed in Sect. 3, with a discussion in Sect. 4 and a conclusion in Sect. 5.
2 Methods
We now explain in more detail the components of the framework. First, we detail the statistical and image-based biplanar reconstruction method, which is performed on biplanar X-rays taken at baseline or follow-up prior to surgery. The model is then used to estimate the parametric torsion index at the transition zones (e.g. at the junction of the thoracic and lumbar segments). Finally, the torsion estimator is used to classify patients and identify different subgroups from the studied population.
2.1 Training Data
The statistical model used for the initial 3D reconstruction is built from a dataset of 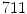 spine models, demonstrating several types of deformities. Each scoliotic spine in the database was obtained from biplanar stereo-reconstructions. It is modeled with 12 thoracic and 5 lumbar vertebrae (17 in total), represented by 6 landmarks on each vertebra (4 pedicle extremities and 2 endplate center points), which were annotated by a radiologist. Segmentation of the scoliotic vertebrae on the X-ray images was performed by using generic vertebra priors obtained from serial CT-scan reconstructions of a cadaver specimen. Models were segmented using a connecting cube algorithm [11] with 1-mm-thick CT-scan slices taken at 1-mm steps throughout the dry spine. The atlas is composed of 17 cadaver vertebrae (12 thoracic and 5 lumbar). The same 6 precise anatomical landmarks (4 pedicle tips and 2 on the vertebral body) were annotated on each individual model.
spine models, demonstrating several types of deformities. Each scoliotic spine in the database was obtained from biplanar stereo-reconstructions. It is modeled with 12 thoracic and 5 lumbar vertebrae (17 in total), represented by 6 landmarks on each vertebra (4 pedicle extremities and 2 endplate center points), which were annotated by a radiologist. Segmentation of the scoliotic vertebrae on the X-ray images was performed by using generic vertebra priors obtained from serial CT-scan reconstructions of a cadaver specimen. Models were segmented using a connecting cube algorithm [11] with 1-mm-thick CT-scan slices taken at 1-mm steps throughout the dry spine. The atlas is composed of 17 cadaver vertebrae (12 thoracic and 5 lumbar). The same 6 precise anatomical landmarks (4 pedicle tips and 2 on the vertebral body) were annotated on each individual model.
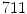 spine models, demonstrating several types of deformities. Each scoliotic spine in the database was obtained from biplanar stereo-reconstructions. It is modeled with 12 thoracic and 5 lumbar vertebrae (17 in total), represented by 6 landmarks on each vertebra (4 pedicle extremities and 2 endplate center points), which were annotated by a radiologist. Segmentation of the scoliotic vertebrae on the X-ray images was performed by using generic vertebra priors obtained from serial CT-scan reconstructions of a cadaver specimen. Models were segmented using a connecting cube algorithm [11] with 1-mm-thick CT-scan slices taken at 1-mm steps throughout the dry spine. The atlas is composed of 17 cadaver vertebrae (12 thoracic and 5 lumbar). The same 6 precise anatomical landmarks (4 pedicle tips and 2 on the vertebral body) were annotated on each individual model.
spine models, demonstrating several types of deformities. Each scoliotic spine in the database was obtained from biplanar stereo-reconstructions. It is modeled with 12 thoracic and 5 lumbar vertebrae (17 in total), represented by 6 landmarks on each vertebra (4 pedicle extremities and 2 endplate center points), which were annotated by a radiologist. Segmentation of the scoliotic vertebrae on the X-ray images was performed by using generic vertebra priors obtained from serial CT-scan reconstructions of a cadaver specimen. Models were segmented using a connecting cube algorithm [11] with 1-mm-thick CT-scan slices taken at 1-mm steps throughout the dry spine. The atlas is composed of 17 cadaver vertebrae (12 thoracic and 5 lumbar). The same 6 precise anatomical landmarks (4 pedicle tips and 2 on the vertebral body) were annotated on each individual model.2.2 Personalized 3D Spine Reconstruction
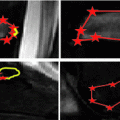
From calibrated coronal and sagittal X-ray images 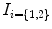 of the patient’s spine, a personalized 3D model is obtained by means of a reconstruction method merging statistical and image-based models based on our previous work [12], and summarized in Fig. 1. The approximate 3D spine centerline
of the patient’s spine, a personalized 3D model is obtained by means of a reconstruction method merging statistical and image-based models based on our previous work [12], and summarized in Fig. 1. The approximate 3D spine centerline 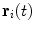 , obtained from quadratic curves extracted from the images is first embedded onto the 3D database of scoliotic spines (M) to predict an initial spine, modeled by 17: (N) vertebrae (12 thoracic, 5 lumbar), 6 points per vertebra (4 pedicle tips and 2 endplate midpoints). To map the high-dimensional 3D curve
, obtained from quadratic curves extracted from the images is first embedded onto the 3D database of scoliotic spines (M) to predict an initial spine, modeled by 17: (N) vertebrae (12 thoracic, 5 lumbar), 6 points per vertebra (4 pedicle tips and 2 endplate midpoints). To map the high-dimensional 3D curve 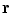 assumed to lie on a non-linear manifold into a low-dimensional subspace, we first determine the manifold reconstruction weights
assumed to lie on a non-linear manifold into a low-dimensional subspace, we first determine the manifold reconstruction weights 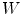 to reconstruct point
to reconstruct point 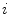 from it’s
from it’s 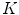 neighbors, and then determine the global internal coordinates of
neighbors, and then determine the global internal coordinates of 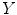 by solving
by solving 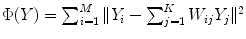 .
.
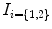 of the patient’s spine, a personalized 3D model is obtained by means of a reconstruction method merging statistical and image-based models based on our previous work [12], and summarized in Fig. 1. The approximate 3D spine centerline
of the patient’s spine, a personalized 3D model is obtained by means of a reconstruction method merging statistical and image-based models based on our previous work [12], and summarized in Fig. 1. The approximate 3D spine centerline 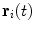 , obtained from quadratic curves extracted from the images is first embedded onto the 3D database of scoliotic spines (M) to predict an initial spine, modeled by 17: (N) vertebrae (12 thoracic, 5 lumbar), 6 points per vertebra (4 pedicle tips and 2 endplate midpoints). To map the high-dimensional 3D curve
, obtained from quadratic curves extracted from the images is first embedded onto the 3D database of scoliotic spines (M) to predict an initial spine, modeled by 17: (N) vertebrae (12 thoracic, 5 lumbar), 6 points per vertebra (4 pedicle tips and 2 endplate midpoints). To map the high-dimensional 3D curve 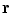 assumed to lie on a non-linear manifold into a low-dimensional subspace, we first determine the manifold reconstruction weights
assumed to lie on a non-linear manifold into a low-dimensional subspace, we first determine the manifold reconstruction weights 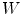 to reconstruct point
to reconstruct point 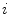 from it’s
from it’s 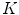 neighbors, and then determine the global internal coordinates of
neighbors, and then determine the global internal coordinates of 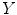 by solving
by solving 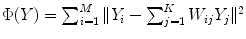 .
.The projection point 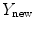 is used to generate an appropriately scaled model from an analytical method based on nonlinear regression using a Radial Basis Function kernel function
is used to generate an appropriately scaled model from an analytical method based on nonlinear regression using a Radial Basis Function kernel function 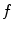 , with D is the dimensionality of the spine and
, with D is the dimensionality of the spine and 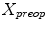 to perform the inverse mapping such that
to perform the inverse mapping such that ![$$X_\mathrm{preop }=[f_{1}(Y_\mathrm{new }),...,f_{D}(Y_\mathrm{new })]$$](/wp-content/uploads/2016/03/A323246_1_En_7_Chapter_IEq16.gif) with
with 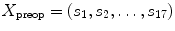 , where
, where 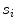 is a vertebra model defined by
is a vertebra model defined by 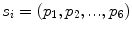 , and
, and 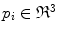 is a 3D vertebral landmark.
is a 3D vertebral landmark.
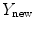 is used to generate an appropriately scaled model from an analytical method based on nonlinear regression using a Radial Basis Function kernel function
is used to generate an appropriately scaled model from an analytical method based on nonlinear regression using a Radial Basis Function kernel function 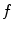 , with D is the dimensionality of the spine and
, with D is the dimensionality of the spine and 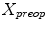 to perform the inverse mapping such that
to perform the inverse mapping such that ![$$X_\mathrm{preop }=[f_{1}(Y_\mathrm{new }),...,f_{D}(Y_\mathrm{new })]$$](/wp-content/uploads/2016/03/A323246_1_En_7_Chapter_IEq16.gif) with
with 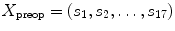 , where
, where 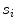 is a vertebra model defined by
is a vertebra model defined by 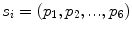 , and
, and 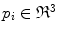 is a 3D vertebral landmark.
is a 3D vertebral landmark.This crude statistical 3D model is refined with an individual scoliotic vertebra segmentation approach by extending 2D geodesic active regions in 3D, in order to evolve prior deformable 3D surfaces by level sets optimization. An atlas of vertebral meshes 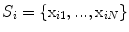 with triangles
with triangles 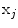 are initially positioned and oriented from their respective 6 precise landmarks
are initially positioned and oriented from their respective 6 precise landmarks 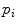 . The surface evolution is then regulated by the gradient map and image intensity distributions [13], where
. The surface evolution is then regulated by the gradient map and image intensity distributions [13], where 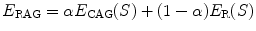 is the energy function with the edge and region-based components controlled by
is the energy function with the edge and region-based components controlled by 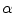 determined empirically, are defined as:
determined empirically, are defined as:
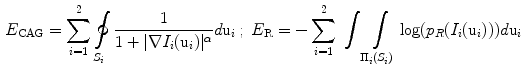
with 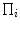 as the perspective projection parameters, and
as the perspective projection parameters, and 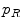 is a Gaussian distribution. The projected silhouettes of the morphed 3D models would therefore match the 2D information on the biplanar X-rays in the image domain
is a Gaussian distribution. The projected silhouettes of the morphed 3D models would therefore match the 2D information on the biplanar X-rays in the image domain 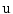 , replicating the specifics of a particular scoliotic deformity. At the end of process, the 3D landmark coordinates
, replicating the specifics of a particular scoliotic deformity. At the end of process, the 3D landmark coordinates 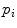 and corresponding polygonal vertebral meshes
and corresponding polygonal vertebral meshes 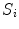




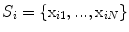 with triangles
with triangles 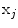 are initially positioned and oriented from their respective 6 precise landmarks
are initially positioned and oriented from their respective 6 precise landmarks 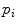 . The surface evolution is then regulated by the gradient map and image intensity distributions [13], where
. The surface evolution is then regulated by the gradient map and image intensity distributions [13], where 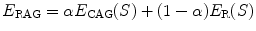 is the energy function with the edge and region-based components controlled by
is the energy function with the edge and region-based components controlled by 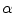 determined empirically, are defined as:
determined empirically, are defined as: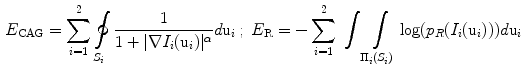
(1)
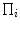 as the perspective projection parameters, and
as the perspective projection parameters, and 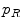 is a Gaussian distribution. The projected silhouettes of the morphed 3D models would therefore match the 2D information on the biplanar X-rays in the image domain
is a Gaussian distribution. The projected silhouettes of the morphed 3D models would therefore match the 2D information on the biplanar X-rays in the image domain 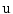 , replicating the specifics of a particular scoliotic deformity. At the end of process, the 3D landmark coordinates
, replicating the specifics of a particular scoliotic deformity. At the end of process, the 3D landmark coordinates 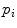 and corresponding polygonal vertebral meshes
and corresponding polygonal vertebral meshes 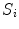
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree