30 days after injury) and chronic (44], occurs later under apoptotic cellular signal, being driven by neuronal deafferentation and axonal damage; the resulting effect on a macroscopic level is that of a progressive brain matter atrophy, measurable as brain volume reduction [44].
1.5 Clinical Relevance of Outcome Prediction
1.6 Brain Volume as a Biomarker: From Benchmark to Bedside
1.7 Monitoring the Recovery
2 MRI Brain Segmentation
2.1 Graph-Based Segmentation
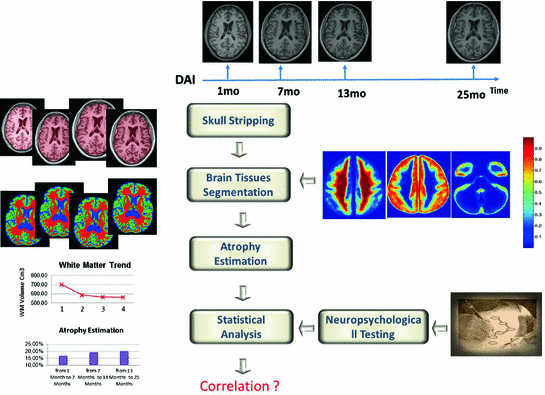
3 Proposed Multidisciplinary Study
 . Then we post-elaborate these sequences with graph-based morphometry analysis techniques in order to segment 26 the brain tissues and measure WM, GM and CSF volumes. The cognitive recovery is monitored by neuropsychologic evaluation performed 6 month, 1 and 2 years post-trauma (according to patient clinical condition) Our tests battery is composed by Mini Mental State Examination (MMSE), Trail making test (TMTA, TMTB), Frontal Assessment Battery (FAB), Wisconsin card sorting test (WCST), phonemic and semantic fluencies, Token test, Rey Auditory Verbal Learning Test (RAVLT), Rey figure, Story recall test, Raven progressive matrix , stroop test, beck depression inventory. The brain volume trajectory and cognitive neuropsychometric trajectory are then coupled and analyzed together to find out correlations on a patient level and on a population level. The overall scheme of our procedure is shown in Fig. 1
. Then we post-elaborate these sequences with graph-based morphometry analysis techniques in order to segment 26 the brain tissues and measure WM, GM and CSF volumes. The cognitive recovery is monitored by neuropsychologic evaluation performed 6 month, 1 and 2 years post-trauma (according to patient clinical condition) Our tests battery is composed by Mini Mental State Examination (MMSE), Trail making test (TMTA, TMTB), Frontal Assessment Battery (FAB), Wisconsin card sorting test (WCST), phonemic and semantic fluencies, Token test, Rey Auditory Verbal Learning Test (RAVLT), Rey figure, Story recall test, Raven progressive matrix , stroop test, beck depression inventory. The brain volume trajectory and cognitive neuropsychometric trajectory are then coupled and analyzed together to find out correlations on a patient level and on a population level. The overall scheme of our procedure is shown in Fig. 1
3.1 Graph-Based Brain Tissues Volumety
3.1.1 Whole Brain Segmentation
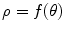 characterized by the following feasibility constraints:
characterized by the following feasibility constraints:
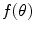 is single valued and the value
is single valued and the value 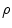 exists for each
exists for each 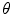 with
with 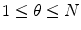 .
.
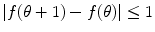 for
for 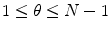 .
.
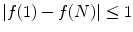 imposing that the first and last pixels satisfy the connectivity constraint.
imposing that the first and last pixels satisfy the connectivity constraint.
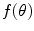 is a candidate object boundary. The goal is then to find the minimum cost boundary subject to the feasibility constraints. The boundary detection task within the graph searching framework is modeled by embedding the properties of the boundary in a cost function and formulating the boundary extraction as the problem of minimizing this function subject to the feasibility constraints. The boundary cost is defined as follows:
is a candidate object boundary. The goal is then to find the minimum cost boundary subject to the feasibility constraints. The boundary detection task within the graph searching framework is modeled by embedding the properties of the boundary in a cost function and formulating the boundary extraction as the problem of minimizing this function subject to the feasibility constraints. The boundary cost is defined as follows:
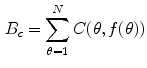
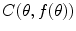 is a cost image. The value of each pixel in the cost image must be inversely related to the likelihood that an edge is present at that point. The likelihood is usually determined by the application of a low-level local edge operator [67]. In general, the definition of this cost function depends on a priori knowledge on the object to be segmented. The boundary cost allows to express both local and global information that can be incorporated within the constrained minimization strategy for optimal boundary detection. The 2D brain segmentation is accomplished in the three following phases.
is a cost image. The value of each pixel in the cost image must be inversely related to the likelihood that an edge is present at that point. The likelihood is usually determined by the application of a low-level local edge operator [67]. In general, the definition of this cost function depends on a priori knowledge on the object to be segmented. The boundary cost allows to express both local and global information that can be incorporated within the constrained minimization strategy for optimal boundary detection. The 2D brain segmentation is accomplished in the three following phases.![]()
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree


of the Prognostic Relevance of Longitudinal Brain Atrophy in Post-traumatic Diffuse Axonal Injury Using Graph-Based MRI Segmentation Techniques
Some recent studies showed that post-traumatic atrophy is not uniformly diffuse throughout subcortical structures, but involves with the highest rates, the amygdala, hippocampus, thalamus and putamen; loss of volume in the amygdala and hippocampus may contribute to various behavioral and cognitive difficulties that commonly affect head-injured patients, such as lability of mood, heightened irritability, and difficulties with memory and learning. Considering subcortical white matter, we note that a variety of regions experienced marked atrophy, with the most dramatic volume loss occurring in the temporal lobes, superior frontal lobes, precuneus and paracentral lobules. The atrophy seems therefore to have a preferential spatial distribution (regional selectivity. Recent works show that regional morphometry may hold value as a biomarker for recovery after trauma [71].
A concern of families, physicians and neuroscientist involved in the care of patient who sustain a traumatic brain injury is the limited ability to predict long-term neuropsychological and social consequences of such injuries for a given patient [52].
Since most survivors are young and have near normal life expectancy, the possibility of predicting the final outcome of a patient with diffuse axonal injury, assumes great importance because this information can feedback the rehabilitative process with increasing scientific evidence of outcome modulation, when conducted in a proper temporal window.
Therefore there is the need of a clinical biomarker related to the amount of diffuse brain damage, that could be measured in the sub-acute period when the patient is still recovering; the importance of such an indicator is not just to predict the possibility of consciousness restoration, but also to infer about the entity of recovery of higher cerebral functions not contemplated by classical outcome scales, but dramatically related to social functioning of an individual.
Quantitative measurement of change in brain size and shape (e.g., to estimate atrophy) is an important current area of research. New methods of change analysis attempt to improve robustness, accuracy, and extent of automation. In december 2002 A.G. Sorensen, Director of the MGH Martinos NMR Center, introduce the term Neurovolumetrics to emphasize the importance of volumetric image analysis for diagnosis and therapy of neurological diseases. Decision in the setting of clinical neurology mostly rely on qualitative (i.e. visual) interpretation of structural brain images. On visual assessment, for example, global brain atrophy is recognized by an increase of cerebrospinal fluid spaces and shrinkage of parenchymal structures. However such an assessment can detect only macroscopic changes with a rather low level of inter-observer agreement. MRI permits in vivo quantification of brain compartment volume, and has many applications in cognitive, clinical and comparative neuroscience. Quantitative assessment of brain volumes, obtained through volumetric MRI has been increasingly applied in recent years to a wide range of neurologic conditions due to advances in computational technology. Its role should be complementary to that of visual assessment of brain structural images, with the specific aim of improving detection of focal and subtle brain pathology. Volumetric methods are mainly based on brain segmentation, that is the separation of the intracranial content into parenchymal and non-parenchymal tissue classes. We know that recovery trajectory is under the influence of different moderators, such as age, pre-morbid I.Q., years of school education; parameters which are related to cerebral plasticity and connectivity and more in general to the concept of functional reserve. The concept of brain volume as a biomarker for neurodegenerative diseases emerged relatively recent in time and represents a challenging instrument for clinical research.
Based on the experimental assumption that after a mechanical inertial load is brought to axons part of fibers are torn with no possibility to recover while the remaining substain subcritical damage of different entity leading to progressive delayed atrophy [44], we set up a longitudinal multicentric study oriented to track the trajectory of brain volume reduction with respect to the functioning of the brain as measured by neuropsychological tests. Our aim is to collect a great amount of clinical and morphometric data of patient victim of traumatic brain injury (DAI type) in order to find out statistical correlations that would allow us to infer about clinical prognosis. Collecting and analyzing many data would lead us to the realization of a prognostic algorithm, helping us to decide the correct timing and intensity of rehabilitation process. In a previous retrospective study conducted at our institution we analyzed perspectives of using brain volume as a predictor of clinical recovery after TBI with pure DAI pattern, finding statistically significant correlation between cognitive performance scores on tests and reduction of brain WM between two time points.
Proper and accurate quantitative measurement of change in brain size and shape can be achieved through the use of segmentation procedures that minimize the user interaction. Automatic segmentation of the brain in Magnetic Resonance Images is a key task in many neuroscience and medical studies either because the brain is the final anatomical structure of interest or because the automatic extraction facilitates further analysis [2, 30]. Whole brain segmentation is a task available in software such as Brain Visa [72], FSL [58] and Brainsuite [55], however in most cases they give poor results especially in case of tumors located on the border of the brain [30].
The problem of segmenting all or part of the brain in MRI imagery continues to be investigated giving rise to a variety of approaches attempting to satisfy the high accuracy demand in diversified clinical and neuroimaging applications [2, 3, 15, 30]. The rationale behind this effort is to improve upon existing early methods suffering from incorrect detection due to noise, difficulties in assigning threshold in the edge image and over and under estimation. The proposed solutions make use of a single, gray scale 2D or 3D image or multiple MR images with different gray scale contrast [15]. Focusing on whole brain segmentation from gray scale images, the early most intuitive approach proposed is automatic thresholding. The application of this approach to MR brain image segmentation includes works based on iterative, knowledge guided thresholding [13, 65] and histogram analysis [1] complemented in some cases with image processing techniques such as morphological filtering [36]. The solutions proposed suffers in general from the difficulty in setting threshold values and present strong limitations in the presence of inhomogeneity, image artefact and anatomical variability.
The Region Growing approach extends thresholding by combining it with connectivity. Methods within this approach need an operator for manual setting of seed for each region and their results depend on the heuristic assessment of thresholding for homogeneity [17, 45]. As a consequence, suitable accuracy is achieved only detecting the contour in slices where the brain is one homogeneous region without pathological alterations and inhomogeneity.
Supervised statistical pattern recognition approaches are proposed in MR image segmentation to circumvent the problem of explicitly and analytically describing the specific segmentation procedure and related parameters, lying to a learning stage the charge of inducing the classifier from supervised data available. Parametric and non parametric methods are proposed showing a competitive behavior in reducing the effect of Radio Frequency (RF) inhomogeneity but requiring some interaction to provide tissue training pixels and to perform post processing adjustments [16, 28]. The parametric probabilistic classification is sensitive to accurate estimation of the probability density function (PDF) [60]. Nonparametric approaches obtain the parameters of the PDF from data without any assumptions, so these approaches are accurate but expensive [14, 40]. Computational complexity and low generalization of trained classifiers limit their applicability. Unsupervised methods employed for MR brain image segmentation include K-Means and its fuzzy equivalent Fuzzy c-Means (FCM) [25]. From a viewpoint of reproducibility, unsupervised methods are clearly desirable. Many algorithms are introduced to make FCM robust against noise and inhomogeneity but most of them still present low accuracy [26, 73]. Other pattern recognition methods such as neural networks and template matching have been also applied to MR brain image segmentation [26, 68].
Edge-based segmentation approaches have been widely investigated to segment MR images of the head [8, 15, 19]. Base methods apply local operations to every point of the input picture, in order to extract short edge elements. Some of these operations are very simple, like the gradient or the Laplacian, whereas other operations are more complex and allow the elimination of most of the local noise [4]. When small edge elements have been obtained, edge following strategies are applied to connect them to form borders. Snell et al. use an active surface template to find the intracranial boundary in MRI volumes of the head [59]. The method is based on the active contour model algorithm “Snakes” [29]. However the resulting procedure requires user interaction to provide a good initial contour for subsequent snake contour refinement. The Bayesian dynamic contour (BDC) model [35] shows advantages over the snakes active contour as the energy functions used to find the boundary can be more generally based on information about the whole region, rather than just the local boundary characteristics. The results are promising for the central slices of multispectral images presented, but have yet to be developed for isolating the whole brain. Contour-based deformable models are applied successfully to MRI brain segmentation although the approach suffer from the difficulty of determining the initial contour and tuning parameters [1, 30]. Khotanlou et al. [30] explicitly propose a segmentation method based on deformable models and asymmetry analysis. Proceeding from the assumption that in normal brain the symmetry plane of the head is approximately equal to the symmetry plane of the segmented brain, a MRI brain segmentation algorithm robust in presence of tumor has been developed. Results obtained are satisfactorily but they heavily depend from the validity of the symmetry assumption.
A boundary tracing method using dynamic programming for noisy brain sections with vague boundaries, is proposed but successful application for global segmentation of MR images remains to be demonstrated since a good initial guess for the boundaries is required [70]. Of the many techniques available for automated border detection, those based on graph searching principles [37] have been successful in several applications.
The value of graph search method lies in robustness which derives from the property typical of the optimization methods of embedding global information about edges and the structure of object in a figure of merit allowing accurate border detection from noisy pictures [41]. Graph searching has become one of the best investigated segmentation tool for medical image data with applications to coronary angiography, ultrasound and cardiac MRI imaging [21, 62, 64, 67]. However, to the best of our knowledge the application of this technique to MRI brain segmentation has not yet investigated. In early works the analysis of the entire volume of data was usually accomplished by applying 2D contour detection strategy slice-by-slice, conceiving individual slices independent and without incorporating interrelation information of the spatial sequence of images [27].
Graph searching has become one of the best investigated segmentation tool for 2D medical image data [21, 49, 64]. The application of graph search to contour detection was first published in [37] presenting a method for detecting edges and contours in noisy pictures. The overall detection process is transformed into the search for the optimal path in a weighted graph, that connects two specific nodes, the starting and ending nodes. The procedure can then be seen as an edge following procedure that uses global information. The value of graph search segmentation methods lies both in robustness and improvements in computing time. Robustness derives from the fact that it inherits the property of optimization methods of embedding global information about edges and structure of object in a figure of merit, allowing accurate border detection from noisy pictures [41]. The formulation of the optimization problem as a search of the shortest path, allows to use heuristic information to speed up the search, leading to improvements in computing time with respect to other optimization [61].
When dealing with volumetric segmentation, the application, slice-by-slice of 2D graph searching techniques for the identification of 3D object boundary suffers of some limitations essentially due to lack of contextual spatial information.
In recent years, we assist to a wide spread utilization of three dimensional models, often conceived as an extension of previously defined 2D solutions [27]. Unfortunately, standard implementation of graph searching for optimal path cannot be directly applied to perform on optimal surface search. All path-based methods are limited to 2D applications because object boundary in 3D volumes can not be represented by a path. The topic of extending the graph-searching techniques to a direct volumetric medical image segmentation has been investigated in literature [22, 63, 66, 67] giving rise to two main approaches, one acting on graph representation in order to take advantage from the existing search techniques, and the other acting on search algorithm that directly performs an optimal surface determination. Both of them attempt to create a balance between two opposite criteria: to limit the computational complexity and to reach a global optimality. In particular Thedens et al. [67] proposes a method of graph searching belonging to the first category. To make the method efficient, the proposed transformation of the lattice representing the graph imposes the restriction that the number of points to which a single point within the lattice is linked, should be very small and secondly, one dimension of the lattice should be small compared to the other two. The first requirement is satisfied by imposing a smoothness constraint, the second, unfortunately, prevents the applicability of the method to several imaging such as volumetric brain MRI Imaging in which voxels are isotropic and the volume dimensions in the three axis are comparable. The method, applied to MRI cardiac imagery, is computational expensive [2].
A graph cut segmentation method for optimal hypersurface detection was developed by Li et al. [33]. The solution proposed is based on the representation of the problem in terms of a geometric graph and on the computation of a minimum s-t cut in a derived directed graph of reduced complexity [12]. The Graph Cut framework for segmentation is based on an implicit representation of object boundaries. Thus, it allows the same flexible topological properties of segments as in techniques where the edge properties are explicit, level-sets for example [54]. Since the introduction of the approximation energy minimization via Graph Cut proposed by Boykov et al. [12] and the subsequent technique formalization for solving segmentation problem on N-D Images [9, 10], many methods have been proposed to solve problems or emphasize features of the classic Graph Cut.
The Graph Cut has undergone evolutions in different directions: some with the aim of improving the interactivity [53], other incorporating other techniques as watershed or gaussian mixture model [6, 48] and other integrating high-level contextual information [32]. In this Chapter we address two MRI Brain Segmentation tasks adopting different graph-based segmentation methods. The first task consists in the fully automatic whole brain segmentation from MRI volume. We derive our method from the edge-based approach adopting Graph Searching tecnique [37] for 2D boundary detection. The solutions investigated in this paper are an extension of those adopted in a previous work [41] from which we inherit the graph searching model. The MRI volume is processed slice by slice, the overall segmentation procedure is made fully automatic and easily reproducible by the automatic detection of frames including eyes and by computing the internal main parameters directly from the image data in this Chapter are reported the salient aspect of the method are reported all the details are reported in [46, 47].
The second task concerns the segmentation of the different brain tissues White Matter, Gray Matter and Cerebral Spinal Fluid in order to be able to study if the atrophy of these tissues are biomarkers for neurodegenerative diseases. For achieving this task a modified Graph Cut method is used that incorporates in the energy function a component related to a-priori information on the spatial distribution of tissues already used by the authors in [42].
Fig. 1
Scheme of the proposed multidisciplinary study for for evaluating the prognostic relevance of longitudinal brain atrophy estimation in post-traumatic DAI
Our multidisciplinary study recruites patients with pure DAI lesion pattern on MRI, being in a state of coma of sudden onset, whit no history of psychiatric disease, alcohol or drugs abuse, previous head trauma or brain intervention, with no incompatibility for MRI examination. The first MRI is performed for clinical need of making diagnosis of DAI that could explain the counsciosness impairment in the absence of focal brain lesion on CT examination. Then, after submittion of written informed consent by the relatives, the patient is MRI-scanned at four time points : 1 month post-trauma, 6 month, 1 and 2 years later. The acquisition sequence is 3D T1 MP-RAGE isotropic with voxel of 1 mm
The overall procedure to extract the volume changes of White Matter (WM), Gray Matter (GM) and Cerebral Spinal Fluid (CSF) is composed of two essential steps. The aim of the first phase is to segment the whole brain from the head MRI and the aim of the second phase is to cluster WM, FM and CSF for examining separately the changes in volume over time of the three classes.
We briefly describe the key points of this strategy.
A contour of radial shape can be conveniently treated by using polar coordinates. Working in polar space, the radial boundary of a given object can be represented by a transformation
Boundary as a Function
Connectivity Constraint
Closing Constraint
Each feasible function where
(1)
