of a set of 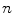 landmarks
landmarks 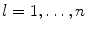 on each, a statistical shape model is trained by applying principal component analysis (PCA) to the aligned shapes [2]. This yields a linear model of shape variation, which represents the position of each landmark
on each, a statistical shape model is trained by applying principal component analysis (PCA) to the aligned shapes [2]. This yields a linear model of shape variation, which represents the position of each landmark 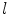 using
using
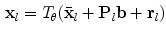
(1)
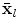 is the mean position of the point in a suitable reference frame,
is the mean position of the point in a suitable reference frame, 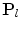 is a set of modes of variation,
is a set of modes of variation, 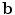 are the shape parameters,
are the shape parameters, 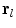 allows small deviations from the model, and
allows small deviations from the model, and 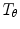 applies a global transformation (e.g. similarity) with parameters
applies a global transformation (e.g. similarity) with parameters 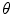 .
.To match the model to a query image, 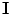 , the overall quality of fit
, the overall quality of fit 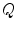 , of the model to the image is optimised over parameters
, of the model to the image is optimised over parameters 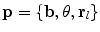
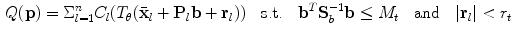
where 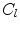 is a cost image for the fitting of landmark
is a cost image for the fitting of landmark 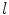 ,
, 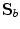 is the covariance matrix of shape model parameters
is the covariance matrix of shape model parameters 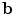 ,
, 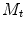 is a threshold on the Mahalanobis distance, and
is a threshold on the Mahalanobis distance, and 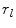 is a threshold on the residuals.
is a threshold on the residuals. 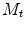 is chosen using the cumulative distribution function (CDF) of the
is chosen using the cumulative distribution function (CDF) of the 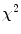 distribution so that 98 % of samples from a multivariate Gaussian of the appropriate dimension would fall within it. This ensures a plausible shape by assuming a flat distribution for model parameters
distribution so that 98 % of samples from a multivariate Gaussian of the appropriate dimension would fall within it. This ensures a plausible shape by assuming a flat distribution for model parameters 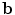 constrained within hyper-ellipsoidal bounds [2]. In the original work [2],
constrained within hyper-ellipsoidal bounds [2]. In the original work [2], 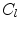 was provided by normalised correlation with a globally constrained patch model.
was provided by normalised correlation with a globally constrained patch model.
 , the overall quality of fit
, the overall quality of fit 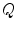 , of the model to the image is optimised over parameters
, of the model to the image is optimised over parameters 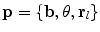
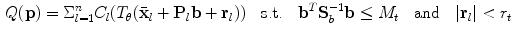
(2)
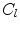 is a cost image for the fitting of landmark
is a cost image for the fitting of landmark 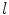 ,
, 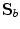 is the covariance matrix of shape model parameters
is the covariance matrix of shape model parameters 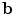 ,
, 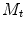 is a threshold on the Mahalanobis distance, and
is a threshold on the Mahalanobis distance, and 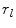 is a threshold on the residuals.
is a threshold on the residuals. 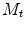 is chosen using the cumulative distribution function (CDF) of the
is chosen using the cumulative distribution function (CDF) of the 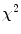 distribution so that 98 % of samples from a multivariate Gaussian of the appropriate dimension would fall within it. This ensures a plausible shape by assuming a flat distribution for model parameters
distribution so that 98 % of samples from a multivariate Gaussian of the appropriate dimension would fall within it. This ensures a plausible shape by assuming a flat distribution for model parameters 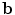 constrained within hyper-ellipsoidal bounds [2]. In the original work [2],
constrained within hyper-ellipsoidal bounds [2]. In the original work [2], 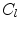 was provided by normalised correlation with a globally constrained patch model.
was provided by normalised correlation with a globally constrained patch model.RF Regression Voting in the CLM Framework. In RFRV-CLM, 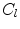 in Eq. 2 is provided by voting with a Random-Forest (RF) regressor. To train the RF for a single landmark, the shape model is used to assess the global pose,
in Eq. 2 is provided by voting with a Random-Forest (RF) regressor. To train the RF for a single landmark, the shape model is used to assess the global pose, 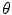 , of the object in each image by minimising
, of the object in each image by minimising 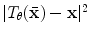 . Each image is resampled into a standardised reference frame by applying the inverse of the estimated pose. The model is scaled so that the width of the reference frame of the mean shape is a given value,
. Each image is resampled into a standardised reference frame by applying the inverse of the estimated pose. The model is scaled so that the width of the reference frame of the mean shape is a given value, 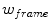 . Sample patches of area
. Sample patches of area 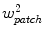 are then generated from the resampled images at a set of random displacements from the true point positions. The displacements
are then generated from the resampled images at a set of random displacements from the true point positions. The displacements 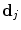 are drawn from a flat distribution in the range
are drawn from a flat distribution in the range ![$$[-d_{ max},+d_{ max}]$$](/wp-content/uploads/2016/10/A331518_1_En_14_Chapter_IEq30.gif) in
in 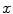 and
and 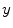 . Finally, image features
. Finally, image features 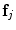 are extracted from the sample patches. Haar-like features [20] are used, as they have proven effective for a range of applications and can be calculated efficiently from integral images. To allow for inaccurate initial estimates of the pose and to make the detector locally pose-invariant, the process is repeated with random perturbations in scale and orientation of the pose estimate. A RF [1] is then trained, using a standard, greedy approach, with the feature vectors
are extracted from the sample patches. Haar-like features [20] are used, as they have proven effective for a range of applications and can be calculated efficiently from integral images. To allow for inaccurate initial estimates of the pose and to make the detector locally pose-invariant, the process is repeated with random perturbations in scale and orientation of the pose estimate. A RF [1] is then trained, using a standard, greedy approach, with the feature vectors 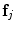 as inputs and the displacements
as inputs and the displacements 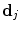 as regression targets. Each tree is trained on a bootstrap sample of
as regression targets. Each tree is trained on a bootstrap sample of 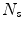 pairs
pairs 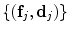 from the training data. At each node, a random sub-set of
from the training data. At each node, a random sub-set of 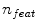 features are chosen from this sample, and a feature
features are chosen from this sample, and a feature 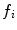 and threshold
and threshold 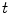 that best split the data into two compact groups are selected by minimising an entropy measure [3]. Splitting terminates at either a maximum depth,
that best split the data into two compact groups are selected by minimising an entropy measure [3]. Splitting terminates at either a maximum depth, 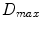 , or a minimum number of samples,
, or a minimum number of samples, 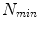 . The process is repeated to generate a forest of size
. The process is repeated to generate a forest of size 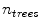 .
.
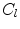 in Eq. 2 is provided by voting with a Random-Forest (RF) regressor. To train the RF for a single landmark, the shape model is used to assess the global pose,
in Eq. 2 is provided by voting with a Random-Forest (RF) regressor. To train the RF for a single landmark, the shape model is used to assess the global pose, 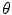 , of the object in each image by minimising
, of the object in each image by minimising 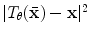 . Each image is resampled into a standardised reference frame by applying the inverse of the estimated pose. The model is scaled so that the width of the reference frame of the mean shape is a given value,
. Each image is resampled into a standardised reference frame by applying the inverse of the estimated pose. The model is scaled so that the width of the reference frame of the mean shape is a given value, 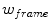 . Sample patches of area
. Sample patches of area 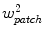 are then generated from the resampled images at a set of random displacements from the true point positions. The displacements
are then generated from the resampled images at a set of random displacements from the true point positions. The displacements 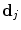 are drawn from a flat distribution in the range
are drawn from a flat distribution in the range ![$$[-d_{ max},+d_{ max}]$$](/wp-content/uploads/2016/10/A331518_1_En_14_Chapter_IEq30.gif) in
in 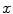 and
and 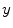 . Finally, image features
. Finally, image features 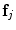 are extracted from the sample patches. Haar-like features [20] are used, as they have proven effective for a range of applications and can be calculated efficiently from integral images. To allow for inaccurate initial estimates of the pose and to make the detector locally pose-invariant, the process is repeated with random perturbations in scale and orientation of the pose estimate. A RF [1] is then trained, using a standard, greedy approach, with the feature vectors
are extracted from the sample patches. Haar-like features [20] are used, as they have proven effective for a range of applications and can be calculated efficiently from integral images. To allow for inaccurate initial estimates of the pose and to make the detector locally pose-invariant, the process is repeated with random perturbations in scale and orientation of the pose estimate. A RF [1] is then trained, using a standard, greedy approach, with the feature vectors 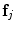 as inputs and the displacements
as inputs and the displacements 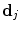 as regression targets. Each tree is trained on a bootstrap sample of
as regression targets. Each tree is trained on a bootstrap sample of 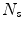 pairs
pairs 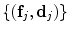 from the training data. At each node, a random sub-set of
from the training data. At each node, a random sub-set of 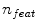 features are chosen from this sample, and a feature
features are chosen from this sample, and a feature 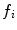 and threshold
and threshold 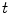 that best split the data into two compact groups are selected by minimising an entropy measure [3]. Splitting terminates at either a maximum depth,
that best split the data into two compact groups are selected by minimising an entropy measure [3]. Splitting terminates at either a maximum depth, 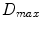 , or a minimum number of samples,
, or a minimum number of samples, 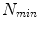 . The process is repeated to generate a forest of size
. The process is repeated to generate a forest of size 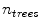 .
.RFRV-CLM Fitting Fitting to a query image is initialised via an estimate of the pose of the model e.g. from a small number of manual point annotations or a previous model, providing initial estimates 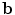 and
and 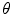 (see Sect. 3). Equation 2 is then optimised as follows. The image is resampled in the reference frame using the current pose. Cost images
(see Sect. 3). Equation 2 is then optimised as follows. The image is resampled in the reference frame using the current pose. Cost images 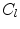 are then computed by evaluating a grid of points in the resampled images over a region of interest around the current estimate of each point; the grid size is defined by a search range
are then computed by evaluating a grid of points in the resampled images over a region of interest around the current estimate of each point; the grid size is defined by a search range ![$$[-d_{search}, +d_{search}]$$](/wp-content/uploads/2016/10/A331518_1_En_14_Chapter_IEq47.gif) , and the cost images are calculated for all landmarks independently. At each point
, and the cost images are calculated for all landmarks independently. At each point 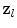 in the grid, the required feature values are extracted and the RF regressor
in the grid, the required feature values are extracted and the RF regressor 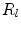 applied.
applied. 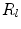 then casts a vote into a cost image
then casts a vote into a cost image 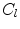 using
using 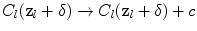 . Each leaf node of the RF contains the mean
. Each leaf node of the RF contains the mean 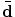 and covariance
and covariance 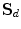 of the random displacements
of the random displacements 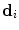 from the true point position, in the reference frame, of its training samples. This supports several voting styles (
from the true point position, in the reference frame, of its training samples. This supports several voting styles (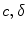 ); a single, unit vote at
); a single, unit vote at 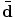 , or probabilistic voting by weighting with
, or probabilistic voting by weighting with 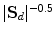 , or by casting a Gaussian spread of votes
, or by casting a Gaussian spread of votes 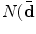 ,
, 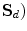 .
.
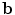 and
and 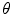 (see Sect. 3). Equation 2 is then optimised as follows. The image is resampled in the reference frame using the current pose. Cost images
(see Sect. 3). Equation 2 is then optimised as follows. The image is resampled in the reference frame using the current pose. Cost images 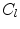 are then computed by evaluating a grid of points in the resampled images over a region of interest around the current estimate of each point; the grid size is defined by a search range
are then computed by evaluating a grid of points in the resampled images over a region of interest around the current estimate of each point; the grid size is defined by a search range ![$$[-d_{search}, +d_{search}]$$](/wp-content/uploads/2016/10/A331518_1_En_14_Chapter_IEq47.gif) , and the cost images are calculated for all landmarks independently. At each point
, and the cost images are calculated for all landmarks independently. At each point 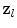 in the grid, the required feature values are extracted and the RF regressor
in the grid, the required feature values are extracted and the RF regressor 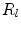 applied.
applied. 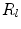 then casts a vote into a cost image
then casts a vote into a cost image 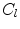 using
using 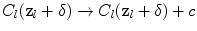 . Each leaf node of the RF contains the mean
. Each leaf node of the RF contains the mean 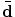 and covariance
and covariance 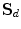 of the random displacements
of the random displacements 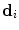 from the true point position, in the reference frame, of its training samples. This supports several voting styles (
from the true point position, in the reference frame, of its training samples. This supports several voting styles (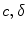 ); a single, unit vote at
); a single, unit vote at 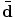 , or probabilistic voting by weighting with
, or probabilistic voting by weighting with 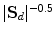 , or by casting a Gaussian spread of votes
, or by casting a Gaussian spread of votes 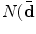 ,
, 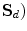 .
.The point positions are re-estimated by finding the lowest cost point within a disk of radius 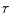 of the current position in each cost image, applying the shape model and moving
of the current position in each cost image, applying the shape model and moving 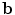 to nearest valid point on the limiting ellipsoid if the shape constraint in Eq. 2 is violated, updating all point positions using
to nearest valid point on the limiting ellipsoid if the shape constraint in Eq. 2 is violated, updating all point positions using 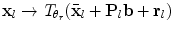 , and iterating whilst reducing
, and iterating whilst reducing 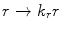 . The initial disk radius
. The initial disk radius 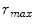 was set to the search range
was set to the search range 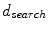 , the search was terminated at
, the search was terminated at 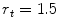 pixels (in the reference image), and
pixels (in the reference image), and 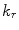 was set to
was set to 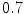 . The optimisation is described in full in Algorithm 1.
. The optimisation is described in full in Algorithm 1.

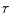 of the current position in each cost image, applying the shape model and moving
of the current position in each cost image, applying the shape model and moving 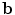 to nearest valid point on the limiting ellipsoid if the shape constraint in Eq. 2 is violated, updating all point positions using
to nearest valid point on the limiting ellipsoid if the shape constraint in Eq. 2 is violated, updating all point positions using 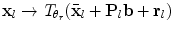 , and iterating whilst reducing
, and iterating whilst reducing 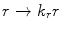 . The initial disk radius
. The initial disk radius 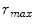 was set to the search range
was set to the search range 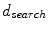 , the search was terminated at
, the search was terminated at 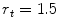 pixels (in the reference image), and
pixels (in the reference image), and 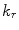 was set to
was set to 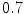 . The optimisation is described in full in Algorithm 1.
. The optimisation is described in full in Algorithm 1.
3 Evaluation
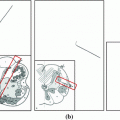
A series of experiments was performed to optimise the various free parameters and options of the RFRV-CLM for application to the task of vertebral localisation in DXA images, and to compare the results to those achieved in [17] using AAMs. To facilitate this comparison, the same dataset and performance metrics were used. The dataset consisted of 320 DXA VFA images scanned on various Hologic (Bedford MA) scanners, obtained from: (a) 44 patients from a previous study [14]; (b) 80 female subjects in an epidemiological study of a UK cohort born in 1946; (c) 196 females attending a local clinic for DXA BMD measurement, and for whom the referring physician had also requested VFA (as approved by the local ethics committee). Manual annotations of 405 landmarks were available for each image, covering the thoracic vertebrae from T7 to T12 and the lumbar vertebrae from L1 to L4. Each of these vertebrae in each image was also classified by an expert radiologist into one of five groups (normal, deformed but not fractured, and grade 1, 2 and 3 fractures according to the Genant definitions [10]; see Fig. 1).
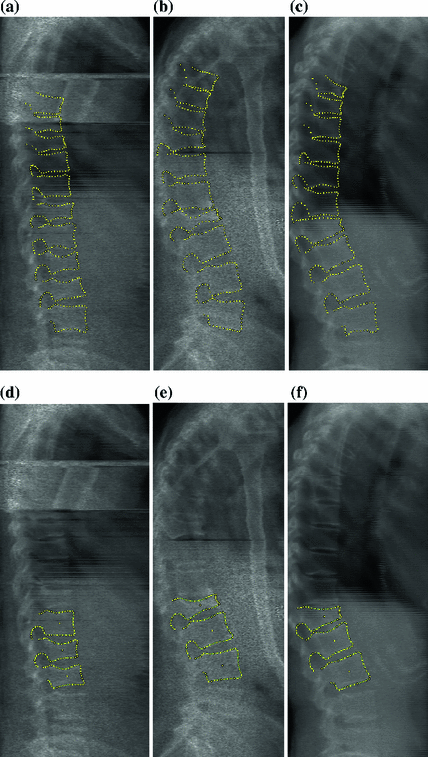

Fig. 1




Example DXA spinal images. a–c 405-point manual annotations. d–f Automatic annotation of the L2 vertebra (using the L1-L3 model), using the fully optimised, 2-stage RFRV-CLM. Example (a, d) shows grade 2 fractures on L2 and L3, (b, e) show a grade 3 fracture on L1, and (c, f) show a grade 3 fracture on L1 and a grade 1 fracture on L2
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree