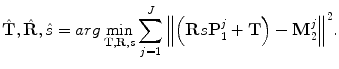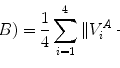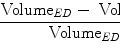and Dorin Comaniciu1
(1)
Imaging and Computer Vision, Siemens Corporate Technology, Princeton, NJ, USA
Abstract
To improve the shape initialization accuracy, this chapter presents the computation of an optimal mean shape that can represent better the whole shape population. The anisotropic similarity transformation from the optimal mean shape to each individual training shape provides the ground truth of the pose parameters learned through the Marginal Space Learning (MSL). After the alignment with the estimated object pose, the optimal mean shape provides more accurate initialization than the mean shapes derived through a bounding box. Experiments on aortic valve landmark detection and whole-heart segmentation demonstrate the advantages of the approach.
6.1 Introduction
In Marginal Space Learning (MSL) based nonrigid object segmentation , the segmentation process contains two stages: pose estimation and boundary delineation. After estimating the pose of the target object, a pre-calculated mean shape is aligned to the estimated pose to provide an initial shape for the final boundary delineation. Nonrigid deformation is present in almost all anatomical structures across different patients or even for the same patient under different physiological states (e.g., a beating heart at different cardiac phases). How to define the pose of a nonrigid shape is still a problem being researched , although heuristic solutions may exist for specific applications.
In the original MSL, the ground truth of the object pose parameters (position, orientation, and scale) of a training sample is determined by using a bounding box of the annotated mesh . The mean shape is calculated as the average of the normalized shapes in the training set in an object-oriented coordinate system. Such solution does not provide optimality. Since the goal of automatic pose estimation is often to provide an accurate shape initialization for the following segmentation or boundary delineation, in this chapter, we present a method to calculate the optimal mean shape, together with the corresponding optimal pose parameters from a training set to minimize the initialization error. An optimization based approach is defined to generate an optimal mean shape from the training set and the corresponding pose parameters for each training shape. Different to the bounding box based approach that determines the object pose for each training sample independently, the proposed method is based on the optimization on the whole training set.
With the optimally determined pose parameters, the MSL is then applied to learn the intrinsic relationship of the image data and the corresponding target object pose. Such relationship is embedded into the MSL classifiers, which are then applied to unseen data for automatic object detection. Experiments show that the proposed method reduces the shape initialization error not only on the training set, but also on the unseen test set. The final segmentation error can be reduced as well due to the more accurate shape initialization . Note that we only change the training step in calculating the optimal mean shape and extracting the pose ground truth of the annotated training samples. There is no computation overhead during the object detection on unseen data.
The remainder of this chapter is organized as follows. We first review the initial bounding box based approach in Sect. 6.2. The optimal mean shape for nonrigid shape initialization is presented in Sect. 6.3. The process is formulated as a generalized Procrustes analysis problem and we then discuss how to align shapes under the similarity transformation and anisotropic similarity transformation. The accuracy of the optimal mean shape is demonstrated on the experiments on aortic valve landmark detection in C-arm Computed Tomography (CT) (Sect. 6.4) and whole-heart segmentation in cardiac CT data (Sect. 6.5). This chapter concludes with Sect. 6.6.
6.2 Heuristic Mean Shape Using a Bounding Box Based Approach
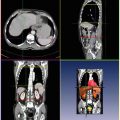
The heuristic approach for calculating a mean shape based on oriented bounding boxes [24, 25] is implemented as follows. For each object, we define an object-orientated coordinate system and calculate the aligned bounding box of the object boundary points, often presented as a surface mesh. Different methods may be used to define the object-oriented coordinate system for different applications. For example, for whole-heart segmentation , the heart coordinate system can be defined based on three landmarks, namely, the aortic valve center, the mitral valve center, and the Left Ventricle (LV) endocardium apex. This local coordinate system actually defines a rotation matrix R for the transformation between the heart-oriented coordinate system and the world coordinate system . We then calculate a bounding box of the mesh points, aligned with the local coordinate system. The bounding box center gives us the position ground truth X t , Y t , and Z t , and the box size along each side defines the ground truth of scaling 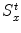 ,
, 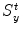 , and
, and 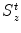 .
.
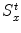 ,
, 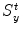 , and
, and 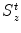 .
.For each training shape, using the above method, we can calculate its position (T = [X, Y, Z]′), orientation (represented as a rotation matrix R), and anisotropic scaling (![$$\mathbf{S} = [S_{x},S_{y},S_{z}]^{\prime}$$](/wp-content/uploads/2016/08/A314110_1_En_6_Chapter_IEq4.gif) ). The transformation from the world coordinate system, M world , to the object-oriented coordinate system, m object is
). The transformation from the world coordinate system, M world , to the object-oriented coordinate system, m object is
![$$\displaystyle{ \mathbf{M}_{world} = \mathbf{R}\left [\begin{array}{ccc} S_{x}& 0 & 0 \\ 0 &S_{y}& 0 \\ 0 & 0 &S_{z}\\ \end{array} \right ]\mathbf{m}_{object}+\mathbf{T}. }$$](/wp-content/uploads/2016/08/A314110_1_En_6_Chapter_Equ1.gif)
Reversing the transformation, we can calculate the position in the object-oriented coordinate system as
![$$\displaystyle{ \mathbf{m}_{object} = \left [\begin{array}{ccc} \frac{1} {S_{x}} & 0 & 0 \\ 0 & \frac{1} {S_{y}} & 0 \\ 0 & 0 & \frac{1} {S_{z}}\\ \end{array} \right ]{\mathbf{R}}^{-1}\left (\mathbf{M}_{ world} -\mathbf{T}\right ). }$$](/wp-content/uploads/2016/08/A314110_1_En_6_Chapter_Equ2.gif)
![$$\mathbf{S} = [S_{x},S_{y},S_{z}]^{\prime}$$](/wp-content/uploads/2016/08/A314110_1_En_6_Chapter_IEq4.gif) ). The transformation from the world coordinate system, M world , to the object-oriented coordinate system, m object is
). The transformation from the world coordinate system, M world , to the object-oriented coordinate system, m object is![$$\displaystyle{ \mathbf{M}_{world} = \mathbf{R}\left [\begin{array}{ccc} S_{x}& 0 & 0 \\ 0 &S_{y}& 0 \\ 0 & 0 &S_{z}\\ \end{array} \right ]\mathbf{m}_{object}+\mathbf{T}. }$$](/wp-content/uploads/2016/08/A314110_1_En_6_Chapter_Equ1.gif)
(6.1)
![$$\displaystyle{ \mathbf{m}_{object} = \left [\begin{array}{ccc} \frac{1} {S_{x}} & 0 & 0 \\ 0 & \frac{1} {S_{y}} & 0 \\ 0 & 0 & \frac{1} {S_{z}}\\ \end{array} \right ]{\mathbf{R}}^{-1}\left (\mathbf{M}_{ world} -\mathbf{T}\right ). }$$](/wp-content/uploads/2016/08/A314110_1_En_6_Chapter_Equ2.gif)
(6.2)
After normalizing the similarity transformation (with anisotropic scaling), the mean shape is the average over the whole training set
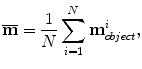
where N is the number of training samples.
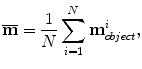
(6.3)
As we can see, the mean shape and the corresponding transformation calculated in this heuristic approach is quite intuitive, however, not optimal from the point of view of how well the mean shape represents the training set.
6.3 Optimal Mean Shape for Nonrigid Shape Initialization
After the MSL based object pose estimation, we align the mean shape to the estimated translation, rotation, and scales as an initial shape for the segmentation process. This initialization needs to be accurate; otherwise, the final boundary evolution may end in a local minimum, due to the clutter of the surrounding tissue around the target object. In this section, we present an optimization based approach to determine the optimal pose parameters and the corresponding mean shape from a training set, thus minimizing the shape initialization error.
6.3.1 Procrustes Optimization for Mean Shape and Pose Parameters
Fig. 6.1
Description of the mathematical symbols used in this chapter
Before going into details, refer to Fig. 6.1 for a description of the mathematic symbols to be used. A group of training shapes,  , are supposed to be given, each shape M i being represented by J points
, are supposed to be given, each shape M i being represented by J points 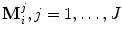 . Point
. Point 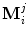 is assumed to have correspondence across volumes. That means it represents the same anatomical position in different volumes. Refer to Chap. 7 for a resampling based approach to establishing mesh point correspondence. To achieve accurate shape initialization, the optimal mean shape
is assumed to have correspondence across volumes. That means it represents the same anatomical position in different volumes. Refer to Chap. 7 for a resampling based approach to establishing mesh point correspondence. To achieve accurate shape initialization, the optimal mean shape 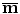 should minimize the residual errors expressed as the Euclidean distance after alignment,
should minimize the residual errors expressed as the Euclidean distance after alignment,
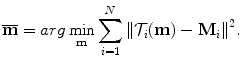
Here, 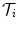 is the corresponding transformation from the mean shape m to each individual shape M i .
is the corresponding transformation from the mean shape m to each individual shape M i .
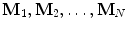 , are supposed to be given, each shape M i being represented by J points
, are supposed to be given, each shape M i being represented by J points 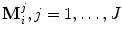 . Point
. Point 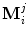 is assumed to have correspondence across volumes. That means it represents the same anatomical position in different volumes. Refer to Chap. 7 for a resampling based approach to establishing mesh point correspondence. To achieve accurate shape initialization, the optimal mean shape
is assumed to have correspondence across volumes. That means it represents the same anatomical position in different volumes. Refer to Chap. 7 for a resampling based approach to establishing mesh point correspondence. To achieve accurate shape initialization, the optimal mean shape 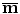 should minimize the residual errors expressed as the Euclidean distance after alignment,
should minimize the residual errors expressed as the Euclidean distance after alignment,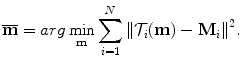
(6.4)
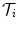 is the corresponding transformation from the mean shape m to each individual shape M i .
is the corresponding transformation from the mean shape m to each individual shape M i .This procedure is called Generalized Procrustes Analysis (GPA) [5] in the shape analysis literature. An iterative approach can be used to search for the locally optimal solution. First, we randomly pick an example shape as a mean shape. We then align each shape to the current mean shape under transformation 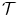 . This step of aligning two shapes is called Procrustes analysis . The average of the aligned shapes (the simple average of the corresponding points) is calculated as a new mean shape. The iterative procedure converges to a locally optimal solution after a few iterations. Note that more involved global optimizations exist for the GPA [16].
. This step of aligning two shapes is called Procrustes analysis . The average of the aligned shapes (the simple average of the corresponding points) is calculated as a new mean shape. The iterative procedure converges to a locally optimal solution after a few iterations. Note that more involved global optimizations exist for the GPA [16].
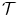 . This step of aligning two shapes is called Procrustes analysis . The average of the aligned shapes (the simple average of the corresponding points) is calculated as a new mean shape. The iterative procedure converges to a locally optimal solution after a few iterations. Note that more involved global optimizations exist for the GPA [16].
. This step of aligning two shapes is called Procrustes analysis . The average of the aligned shapes (the simple average of the corresponding points) is calculated as a new mean shape. The iterative procedure converges to a locally optimal solution after a few iterations. Note that more involved global optimizations exist for the GPA [16].The similarity transformation with isotropic scaling is often used as the transformation 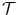 . A few closed-form solutions have been proposed in the literature to align two shapes under the similarity transformation, as discussed in Sect. 6.3.2. However, the MSL can estimate anisotropic scales of an object efficiently. By covering more deformations, the shape space after alignment is more compact and the mean shape can represent the whole shape population more accurately. Therefore, we use the anisotropic similarity transformation to represent the transformation between two shapes. To our knowledge, there are no closed-form solutions for estimating the anisotropic similarity transformation between two shapes. In Sect. 6.3.3 we present a two-step iterative approach to search for the optimal anisotropic transformation.
. A few closed-form solutions have been proposed in the literature to align two shapes under the similarity transformation, as discussed in Sect. 6.3.2. However, the MSL can estimate anisotropic scales of an object efficiently. By covering more deformations, the shape space after alignment is more compact and the mean shape can represent the whole shape population more accurately. Therefore, we use the anisotropic similarity transformation to represent the transformation between two shapes. To our knowledge, there are no closed-form solutions for estimating the anisotropic similarity transformation between two shapes. In Sect. 6.3.3 we present a two-step iterative approach to search for the optimal anisotropic transformation.
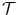 . A few closed-form solutions have been proposed in the literature to align two shapes under the similarity transformation, as discussed in Sect. 6.3.2. However, the MSL can estimate anisotropic scales of an object efficiently. By covering more deformations, the shape space after alignment is more compact and the mean shape can represent the whole shape population more accurately. Therefore, we use the anisotropic similarity transformation to represent the transformation between two shapes. To our knowledge, there are no closed-form solutions for estimating the anisotropic similarity transformation between two shapes. In Sect. 6.3.3 we present a two-step iterative approach to search for the optimal anisotropic transformation.
. A few closed-form solutions have been proposed in the literature to align two shapes under the similarity transformation, as discussed in Sect. 6.3.2. However, the MSL can estimate anisotropic scales of an object efficiently. By covering more deformations, the shape space after alignment is more compact and the mean shape can represent the whole shape population more accurately. Therefore, we use the anisotropic similarity transformation to represent the transformation between two shapes. To our knowledge, there are no closed-form solutions for estimating the anisotropic similarity transformation between two shapes. In Sect. 6.3.3 we present a two-step iterative approach to search for the optimal anisotropic transformation.6.3.2 Procrustes Analysis Under Isotropic Similarity Transformation
Procrustes analysis is a means to remove the translation, rotation, and scaling between two shapes M 1 and M 2,
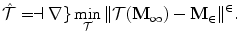
Here, 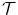 is the transformation between two shapes. The similarity transformation is the most widely used transformation in Procrustes analysis,
is the transformation between two shapes. The similarity transformation is the most widely used transformation in Procrustes analysis,
![$$\displaystyle\begin{array}{rcl} \hat{\mathbf{T}},\hat{\mathbf{R}},\hat{s}& =& arg\min _{\mathbf{T},\mathbf{R},s}{\left \|(s\mathbf{R}\mathbf{M}_{1} + \mathbf{T}) -\mathbf{M}_{2}\right \|}^{2} \\ & =& arg\min _{\mathbf{T},\mathbf{R},s}\sum _{j=1}^{J}{\left \|\mathbf{R}\left [\begin{array}{c} s\mathbf{M}_{1}^{j}(x) \\ s\mathbf{M}_{1}^{j}(y) \\ s\mathbf{M}_{1}^{j}(z)\\ \end{array} \right ] + \mathbf{T} -\left [\begin{array}{c} \mathbf{M}_{2}^{j}(x) \\ \mathbf{M}_{2}^{j}(y) \\ \mathbf{M}_{2}^{j}(z)\\ \end{array} \right ]\right \|}^{2},{}\end{array}$$](/wp-content/uploads/2016/08/A314110_1_En_6_Chapter_Equ6.gif)
where T is translation ; R is a rotation matrix ; and s is a scalar for the isotropic scaling . Various methods have been proposed to estimate the similarity transformation between two point sets (2D or 3D). The closed-form solution based on the singular value decomposition of a covariance matrix of the data is the most elegant [2, 10, 21].
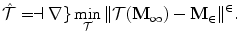
(6.5)
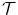 is the transformation between two shapes. The similarity transformation is the most widely used transformation in Procrustes analysis,
is the transformation between two shapes. The similarity transformation is the most widely used transformation in Procrustes analysis,![$$\displaystyle\begin{array}{rcl} \hat{\mathbf{T}},\hat{\mathbf{R}},\hat{s}& =& arg\min _{\mathbf{T},\mathbf{R},s}{\left \|(s\mathbf{R}\mathbf{M}_{1} + \mathbf{T}) -\mathbf{M}_{2}\right \|}^{2} \\ & =& arg\min _{\mathbf{T},\mathbf{R},s}\sum _{j=1}^{J}{\left \|\mathbf{R}\left [\begin{array}{c} s\mathbf{M}_{1}^{j}(x) \\ s\mathbf{M}_{1}^{j}(y) \\ s\mathbf{M}_{1}^{j}(z)\\ \end{array} \right ] + \mathbf{T} -\left [\begin{array}{c} \mathbf{M}_{2}^{j}(x) \\ \mathbf{M}_{2}^{j}(y) \\ \mathbf{M}_{2}^{j}(z)\\ \end{array} \right ]\right \|}^{2},{}\end{array}$$](/wp-content/uploads/2016/08/A314110_1_En_6_Chapter_Equ6.gif)
(6.6)
Suppose mean (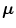 ) and variance (σ) of the point sets for shapes M 1 and M 2 are
) and variance (σ) of the point sets for shapes M 1 and M 2 are
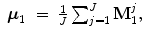
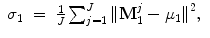
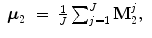
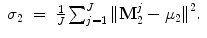
Let 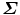 (a 3 × 3 matrix) be the covariance matrix of shapes M 1 and M 2,
(a 3 × 3 matrix) be the covariance matrix of shapes M 1 and M 2,
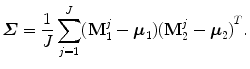
Suppose the singular value decomposition of 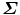 is
is
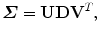
where D is a diagonal matrix; U and V are unitary matrices (i.e., UU T = I and VV T = I, where I is an identity matrix). Then, the optimal estimate of the similarity transformation [21] is
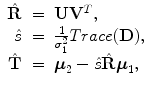
where Trace(D) is the summation of the diagonal elements of matrix D.
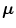 ) and variance (σ) of the point sets for shapes M 1 and M 2 are
) and variance (σ) of the point sets for shapes M 1 and M 2 are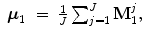
(6.7)
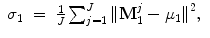
(6.8)
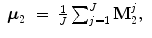
(6.9)
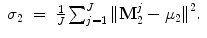
(6.10)
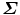 (a 3 × 3 matrix) be the covariance matrix of shapes M 1 and M 2,
(a 3 × 3 matrix) be the covariance matrix of shapes M 1 and M 2,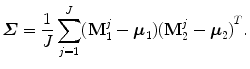
(6.11)
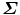 is
is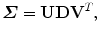
(6.12)
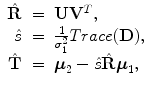
(6.13)
The above closed-form solution works well for most cases. However, under some rare conditions, the estimated transformation may include a reflection (i.e., the determinant of R equals − 1, instead of 1). Umeyama [21] provided a simple fix. The reflection happens when the determinant of the shape covariance matrix 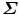 is negative,
is negative, 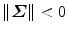 . In singular value decomposition of
. In singular value decomposition of 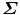 , we can re-organize the elements of matrices D, U, and V so that D = diag(d i ), where d 1 ≥ d 2 ≥ d 3. Let
, we can re-organize the elements of matrices D, U, and V so that D = diag(d i ), where d 1 ≥ d 2 ≥ d 3. Let 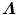 be
be
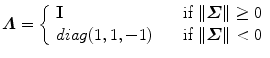
Then, the optimal similarity transformation is
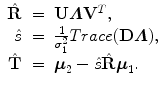
Refer to [21] for a proof of the optimality of this modified solution.
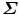 is negative,
is negative, 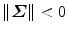 . In singular value decomposition of
. In singular value decomposition of 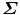 , we can re-organize the elements of matrices D, U, and V so that D = diag(d i ), where d 1 ≥ d 2 ≥ d 3. Let
, we can re-organize the elements of matrices D, U, and V so that D = diag(d i ), where d 1 ≥ d 2 ≥ d 3. Let 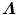 be
be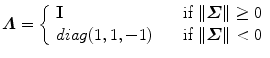
(6.14)
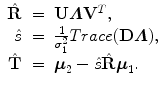
(6.15)
6.3.3 Procrustes Analysis Under Anisotropic Similarity Transformation
The MSL computational framework estimates efficiently the anisotropic scale of an object. The advantage of covering more deformations is that the shape space after alignment is more compact and the mean shape represents the whole shape population more accurately. This is very helpful for many applications, such as the left ventricle detection and segmentation . The deformation of the left ventricle is dominated by contraction and expansion, and the amount of deformation along different directions is quite different. The deformation along the long axis of the left ventricle is usually smaller than the deformation orthogonal to the long axis. Using three scales to represent the size of the ventricle is more accurate than using a single scale. The capability of estimating anisotropic scales is thus important to build a segmentation system working for all cardiac phases.
In this scenario, the anisotropic scaling needs to be compensated during alignment,
![$$\displaystyle{ \hat{\mathbf{T}},\hat{\mathbf{R}},\hat{\mathbf{S}} = arg\min _{\mathbf{T},\mathbf{R},\mathbf{S}}\sum _{j=1}^{J}{\left \|\left (\mathbf{R}\left [\begin{array}{ccc} S_{x}& 0 & 0 \\ 0 &S_{y}& 0 \\ 0 & 0 &S_{z}\\ \end{array} \right ]\mathbf{M}_{1}^{j} + \mathbf{T}\right ) -\mathbf{M}_{ 2}^{j}\right \|}^{2}. }$$](/wp-content/uploads/2016/08/A314110_1_En_6_Chapter_Equ16.gif)
![$$\displaystyle{ \hat{\mathbf{T}},\hat{\mathbf{R}},\hat{\mathbf{S}} = arg\min _{\mathbf{T},\mathbf{R},\mathbf{S}}\sum _{j=1}^{J}{\left \|\left (\mathbf{R}\left [\begin{array}{ccc} S_{x}& 0 & 0 \\ 0 &S_{y}& 0 \\ 0 & 0 &S_{z}\\ \end{array} \right ]\mathbf{M}_{1}^{j} + \mathbf{T}\right ) -\mathbf{M}_{ 2}^{j}\right \|}^{2}. }$$](/wp-content/uploads/2016/08/A314110_1_En_6_Chapter_Equ16.gif)
(6.16)
Since there are no closed-form solutions for the alignment under anisotropic scaling [3], we present a two-step iterative approach to search for an optimal solution. Suppose there is a common scale 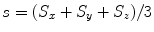 . Let
. Let 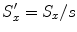 ,
, 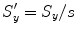 , and
, and 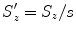 . Equation (6.16) can be re-written as
. Equation (6.16) can be re-written as
![$$\displaystyle{ \hat{\mathbf{T}},\hat{\mathbf{R}},\hat{\mathbf{S}} = arg\min _{\mathbf{T},\mathbf{R},\mathbf{S}}\sum _{j=1}^{J}{\left \|\left (\mathbf{R}s\left [\begin{array}{ccc} S_{x}^{\prime}& 0 & 0 \\ 0 &S_{y}^{\prime}& 0 \\ 0 & 0 &S_{z}^{\prime}\\ \end{array} \right ]\mathbf{M}_{1}^{j} + \mathbf{T}\right ) -\mathbf{M}_{ 2}^{j}\right \|}^{2}. }$$](/wp-content/uploads/2016/08/A314110_1_En_6_Chapter_Equ17.gif)
In the first step, suppose we known the anisotropic scaling factors 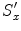 ,
, 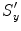 , and
, and 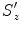 . (At the beginning, we initialize with isotropic scaling,
. (At the beginning, we initialize with isotropic scaling, 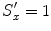 ,
, 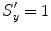 , and
, and 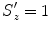 .) We can apply the anisotropic scaling to each point in shape M 1,
.) We can apply the anisotropic scaling to each point in shape M 1,
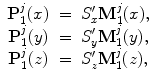
for 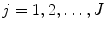 . Equation (6.17) becomes
. Equation (6.17) becomes
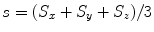 . Let
. Let 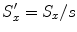 ,
, 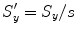 , and
, and 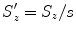 . Equation (6.16) can be re-written as
. Equation (6.16) can be re-written as![$$\displaystyle{ \hat{\mathbf{T}},\hat{\mathbf{R}},\hat{\mathbf{S}} = arg\min _{\mathbf{T},\mathbf{R},\mathbf{S}}\sum _{j=1}^{J}{\left \|\left (\mathbf{R}s\left [\begin{array}{ccc} S_{x}^{\prime}& 0 & 0 \\ 0 &S_{y}^{\prime}& 0 \\ 0 & 0 &S_{z}^{\prime}\\ \end{array} \right ]\mathbf{M}_{1}^{j} + \mathbf{T}\right ) -\mathbf{M}_{ 2}^{j}\right \|}^{2}. }$$](/wp-content/uploads/2016/08/A314110_1_En_6_Chapter_Equ17.gif)
(6.17)
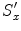 ,
, 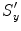 , and
, and 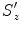 . (At the beginning, we initialize with isotropic scaling,
. (At the beginning, we initialize with isotropic scaling, 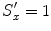 ,
, 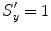 , and
, and 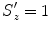 .) We can apply the anisotropic scaling to each point in shape M 1,
.) We can apply the anisotropic scaling to each point in shape M 1,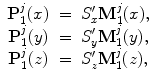
(6.18)
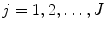 . Equation (6.17) becomes
. Equation (6.17) becomes