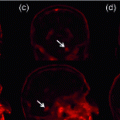
. Simply put, we consider normalized histograms on a grid of locations, and assume the distance between any two locations is provided. Next, we extend Wasserstein distances to non-negative vectors of bounded mass.
Notations. Let d be the cardinal of 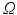 . Relabeling arbitrarily all the elements of
. Relabeling arbitrarily all the elements of 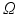 as
as 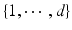 we represent the set of non-negative measures on
we represent the set of non-negative measures on  by the non-negative orthant
by the non-negative orthant 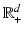 . Let
. Let 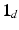 be the d-dimensional vector of ones. For any vector
be the d-dimensional vector of ones. For any vector 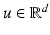 we write
we write 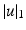 for the
for the 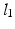 norm of u,
norm of u, 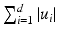 . When
. When 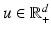 we also call
we also call 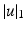 the (total) mass of vector u. Let
the (total) mass of vector u. Let ![$$M=[m_{ij}]\in \mathbb {R}^{d\times d}_+$$](/wp-content/uploads/2016/09/A339424_1_En_20_Chapter_IEq14.gif) be the matrix that describes the metric between all locations in
be the matrix that describes the metric between all locations in  , namely
, namely 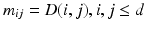 .
.
 . Relabeling arbitrarily all the elements of
. Relabeling arbitrarily all the elements of  as
as 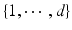 we represent the set of non-negative measures on
we represent the set of non-negative measures on  by the non-negative orthant
by the non-negative orthant 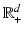 . Let
. Let 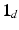 be the d-dimensional vector of ones. For any vector
be the d-dimensional vector of ones. For any vector 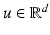 we write
we write 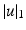 for the
for the 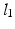 norm of u,
norm of u, 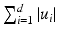 . When
. When 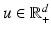 we also call
we also call 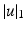 the (total) mass of vector u. Let
the (total) mass of vector u. Let ![$$M=[m_{ij}]\in \mathbb {R}^{d\times d}_+$$](/wp-content/uploads/2016/09/A339424_1_En_20_Chapter_IEq14.gif) be the matrix that describes the metric between all locations in
be the matrix that describes the metric between all locations in 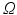 , namely
, namely 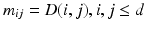 .
.Wasserstein Distance for Normalized Histograms. Consider two vectors 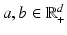 such that
such that 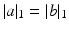 . Both can be interpreted as histograms on
. Both can be interpreted as histograms on 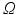 of the same mass. A non-trivial example of such normalized data in medical imaging is the discretized ODF used for diffusion imaging data [10]. For
of the same mass. A non-trivial example of such normalized data in medical imaging is the discretized ODF used for diffusion imaging data [10]. For 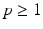 , the p-Wasserstein distance
, the p-Wasserstein distance 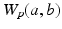 between a and b is the
between a and b is the 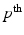 root of the optimum of a linear program, known as a transportation problem [4, §7.2]. A transport problem is a network flow problem on a bipartite graph with cost
root of the optimum of a linear program, known as a transportation problem [4, §7.2]. A transport problem is a network flow problem on a bipartite graph with cost 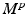 (the pairwise distance matrix M raised element-wise to the power p), and feasible set of flows U(a, b) (known as the transportation polytope of a and b), where U(a, b) is the set of
(the pairwise distance matrix M raised element-wise to the power p), and feasible set of flows U(a, b) (known as the transportation polytope of a and b), where U(a, b) is the set of 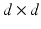 nonnegative matrices such that their row and column marginals are equal to a and b respectively:
nonnegative matrices such that their row and column marginals are equal to a and b respectively:
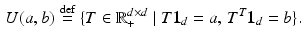
Given the constraints induced by a and b, one naturally has that U(a, b) is empty when 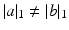 and non-empty when
and non-empty when 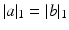 (in which case one can easily check that the matrix
(in which case one can easily check that the matrix 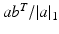 belongs to that set). The p-Wasserstein distance
belongs to that set). The p-Wasserstein distance 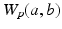 raised to the power p (written
raised to the power p (written 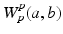 below) is equal to the optimum of a parametric Optimal Transport (
below) is equal to the optimum of a parametric Optimal Transport (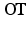 ) problem on
) problem on 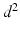 variables,
variables,
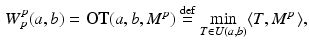
parameterized by the marginals a, b and matrix 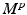 .
.
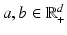 such that
such that 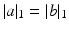 . Both can be interpreted as histograms on
. Both can be interpreted as histograms on 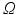 of the same mass. A non-trivial example of such normalized data in medical imaging is the discretized ODF used for diffusion imaging data [10]. For
of the same mass. A non-trivial example of such normalized data in medical imaging is the discretized ODF used for diffusion imaging data [10]. For 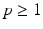 , the p-Wasserstein distance
, the p-Wasserstein distance 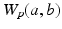 between a and b is the
between a and b is the 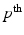 root of the optimum of a linear program, known as a transportation problem [4, §7.2]. A transport problem is a network flow problem on a bipartite graph with cost
root of the optimum of a linear program, known as a transportation problem [4, §7.2]. A transport problem is a network flow problem on a bipartite graph with cost 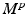 (the pairwise distance matrix M raised element-wise to the power p), and feasible set of flows U(a, b) (known as the transportation polytope of a and b), where U(a, b) is the set of
(the pairwise distance matrix M raised element-wise to the power p), and feasible set of flows U(a, b) (known as the transportation polytope of a and b), where U(a, b) is the set of 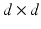 nonnegative matrices such that their row and column marginals are equal to a and b respectively:
nonnegative matrices such that their row and column marginals are equal to a and b respectively: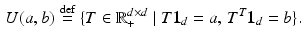
(1)
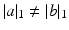 and non-empty when
and non-empty when 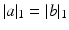 (in which case one can easily check that the matrix
(in which case one can easily check that the matrix 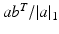 belongs to that set). The p-Wasserstein distance
belongs to that set). The p-Wasserstein distance 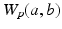 raised to the power p (written
raised to the power p (written 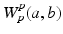 below) is equal to the optimum of a parametric Optimal Transport (
below) is equal to the optimum of a parametric Optimal Transport (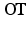 ) problem on
) problem on 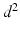 variables,
variables,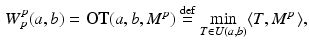
(2)
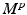 .
.Optimal Transport for Unnormalized Measures. If the total masses of a and b differ, namely 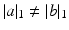 , the definition provided above is not useful because
, the definition provided above is not useful because 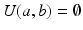 . Several extensions of the OT problem have been proposed in that setting; we recall them here for the sake of completeness. In the computer vision literature, [23] proposed to handle that case by: (i) relaxing the equality constraints of U(a, b) to inequality constraints
. Several extensions of the OT problem have been proposed in that setting; we recall them here for the sake of completeness. In the computer vision literature, [23] proposed to handle that case by: (i) relaxing the equality constraints of U(a, b) to inequality constraints 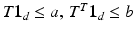 in Eq. (1); (ii) adding an equality constraint on the total mass of the solution
in Eq. (1); (ii) adding an equality constraint on the total mass of the solution 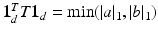 ; (iii) dividing the minimum of
; (iii) dividing the minimum of 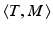 under constraints (i,ii) by
under constraints (i,ii) by 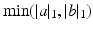 . This modification does not, however, result in a metric. [20] proposed later a variant of this approach called EMD-hat that incorporates constraints (i,ii) but (iii’) adds to the optimal cost
. This modification does not, however, result in a metric. [20] proposed later a variant of this approach called EMD-hat that incorporates constraints (i,ii) but (iii’) adds to the optimal cost 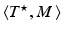 a constant times
a constant times 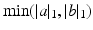 . When that constant is large enough M, [20] claim that EMD-hat is a metric. We also note that [2] proposed a quadratic penalty between the differences of masses and made use of a dynamic formulation of the transportation problem.
. When that constant is large enough M, [20] claim that EMD-hat is a metric. We also note that [2] proposed a quadratic penalty between the differences of masses and made use of a dynamic formulation of the transportation problem.
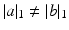 , the definition provided above is not useful because
, the definition provided above is not useful because 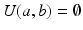 . Several extensions of the OT problem have been proposed in that setting; we recall them here for the sake of completeness. In the computer vision literature, [23] proposed to handle that case by: (i) relaxing the equality constraints of U(a, b) to inequality constraints
. Several extensions of the OT problem have been proposed in that setting; we recall them here for the sake of completeness. In the computer vision literature, [23] proposed to handle that case by: (i) relaxing the equality constraints of U(a, b) to inequality constraints 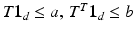 in Eq. (1); (ii) adding an equality constraint on the total mass of the solution
in Eq. (1); (ii) adding an equality constraint on the total mass of the solution 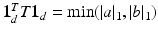 ; (iii) dividing the minimum of
; (iii) dividing the minimum of 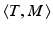 under constraints (i,ii) by
under constraints (i,ii) by 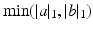 . This modification does not, however, result in a metric. [20] proposed later a variant of this approach called EMD-hat that incorporates constraints (i,ii) but (iii’) adds to the optimal cost
. This modification does not, however, result in a metric. [20] proposed later a variant of this approach called EMD-hat that incorporates constraints (i,ii) but (iii’) adds to the optimal cost 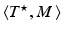 a constant times
a constant times 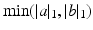 . When that constant is large enough M, [20] claim that EMD-hat is a metric. We also note that [2] proposed a quadratic penalty between the differences of masses and made use of a dynamic formulation of the transportation problem.
. When that constant is large enough M, [20] claim that EMD-hat is a metric. We also note that [2] proposed a quadratic penalty between the differences of masses and made use of a dynamic formulation of the transportation problem.Kantorovich Norms for Signed Measures. We propose to build on early contributions by Kantorovich to define a generalization of optimal transport distance for unnormalized measures, making optimal transport applicable to a wider class of problems, such as the averaging of functional imaging data. [18] proposed such a generalization as an intermediary result of a more general definition, the Kantorovich norm for signed measures on a compact metric space, which was itself extended to separable metric spaces by [15]. We summarize this idea here by simplifying it to the case of interest in this paper where 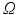 is a finite (of size d) probability space, in which case signed measures are equivalent to vectors in
is a finite (of size d) probability space, in which case signed measures are equivalent to vectors in 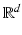 . [18] propose first a norm for vectors z in the orthogonal of
. [18] propose first a norm for vectors z in the orthogonal of 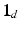 (vectors z such that
(vectors z such that 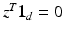 ), by considering the 1-Wasserstein distance between the positive and negative parts of z,
), by considering the 1-Wasserstein distance between the positive and negative parts of z, 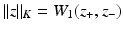 . A penalty vector
. A penalty vector 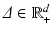 is then introduced to define the norm
is then introduced to define the norm 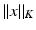 of any vector x as the minimal value of
of any vector x as the minimal value of 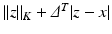 when z is taken in the space of all vectors z with zero sum, and
when z is taken in the space of all vectors z with zero sum, and 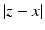 is the element-wise absolute value of the difference of vectors z and x. For this to define a true norm in
is the element-wise absolute value of the difference of vectors z and x. For this to define a true norm in 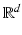 ,
, 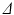 must be such that
must be such that 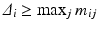 and
and 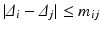 . The distance between two arbitrary non-negative vectors a, b of different mass is then defined as
. The distance between two arbitrary non-negative vectors a, b of different mass is then defined as 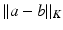 . As highlighted by [26, p.108], and if we write
. As highlighted by [26, p.108], and if we write 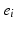 for the
for the 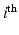 vector of the canonical basis of
vector of the canonical basis of 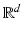 , this norm is the maximal norm in
, this norm is the maximal norm in 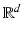 such that for any
such that for any 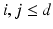 ,
, 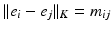 , namely the maximal norm in the space of signed measures on
, namely the maximal norm in the space of signed measures on 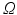 such that the norm between two Dirac measures coincides with
such that the norm between two Dirac measures coincides with 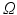 ’s metric between these points.
’s metric between these points.
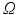 is a finite (of size d) probability space, in which case signed measures are equivalent to vectors in
is a finite (of size d) probability space, in which case signed measures are equivalent to vectors in 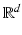 . [18] propose first a norm for vectors z in the orthogonal of
. [18] propose first a norm for vectors z in the orthogonal of 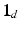 (vectors z such that
(vectors z such that 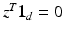 ), by considering the 1-Wasserstein distance between the positive and negative parts of z,
), by considering the 1-Wasserstein distance between the positive and negative parts of z, 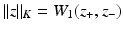 . A penalty vector
. A penalty vector 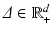 is then introduced to define the norm
is then introduced to define the norm 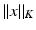 of any vector x as the minimal value of
of any vector x as the minimal value of 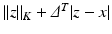 when z is taken in the space of all vectors z with zero sum, and
when z is taken in the space of all vectors z with zero sum, and 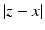 is the element-wise absolute value of the difference of vectors z and x. For this to define a true norm in
is the element-wise absolute value of the difference of vectors z and x. For this to define a true norm in 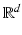 ,
, 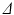 must be such that
must be such that 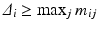 and
and 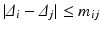 . The distance between two arbitrary non-negative vectors a, b of different mass is then defined as
. The distance between two arbitrary non-negative vectors a, b of different mass is then defined as 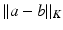 . As highlighted by [26, p.108], and if we write
. As highlighted by [26, p.108], and if we write 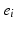 for the
for the 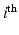 vector of the canonical basis of
vector of the canonical basis of 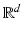 , this norm is the maximal norm in
, this norm is the maximal norm in 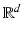 such that for any
such that for any 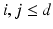 ,
, 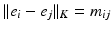 , namely the maximal norm in the space of signed measures on
, namely the maximal norm in the space of signed measures on  such that the norm between two Dirac measures coincides with
such that the norm between two Dirac measures coincides with  ’s metric between these points.
’s metric between these points.Kantorovich Distances for Unnormalized Nonnegative Measures. Reference [14] noticed that Kantorovich’s distance between unnormalized measures can be cast as a regular optimal transport problem. Indeed, one simply needs to: (i) add a virtual point  to the set
to the set 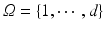 whose distance
whose distance 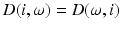 to any element i in
to any element i in 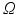 is set to
is set to 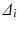 ; (ii) use that point
; (ii) use that point 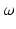 as a buffer when comparing two measures of different mass. The appeal of Kantorovich’s formulation in the context of this work is that it boils down to a classic optimal transport problem, which can be approximated efficiently using the smoothing approach of [6] as discussed in Sect. 3. To simplify our analysis in the next section, we only consider non-negative vectors (histograms)
as a buffer when comparing two measures of different mass. The appeal of Kantorovich’s formulation in the context of this work is that it boils down to a classic optimal transport problem, which can be approximated efficiently using the smoothing approach of [6] as discussed in Sect. 3. To simplify our analysis in the next section, we only consider non-negative vectors (histograms) 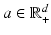 such that their total mass is upper bounded by a known positive constant. This assumption alleviates the definition of our distance below, since it does not require to treat separately the cases where either
such that their total mass is upper bounded by a known positive constant. This assumption alleviates the definition of our distance below, since it does not require to treat separately the cases where either 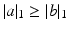 or
or 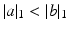 when comparing
when comparing 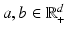 . Note also that this assumption always holds when dealing with finite collections of data. Without loss of generality, this is equivalent to considering vectors a in
. Note also that this assumption always holds when dealing with finite collections of data. Without loss of generality, this is equivalent to considering vectors a in 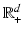 such that
such that 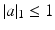 with a simple rescaling of all vectors by that constant. We define next the Kantorovich metric on
with a simple rescaling of all vectors by that constant. We define next the Kantorovich metric on 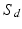 , where
, where 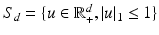 .
.
 to the set
to the set  whose distance
whose distance  to any element i in
to any element i in 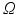 is set to
is set to 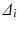 ; (ii) use that point
; (ii) use that point 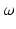 as a buffer when comparing two measures of different mass. The appeal of Kantorovich’s formulation in the context of this work is that it boils down to a classic optimal transport problem, which can be approximated efficiently using the smoothing approach of [6] as discussed in Sect. 3. To simplify our analysis in the next section, we only consider non-negative vectors (histograms)
as a buffer when comparing two measures of different mass. The appeal of Kantorovich’s formulation in the context of this work is that it boils down to a classic optimal transport problem, which can be approximated efficiently using the smoothing approach of [6] as discussed in Sect. 3. To simplify our analysis in the next section, we only consider non-negative vectors (histograms) 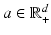 such that their total mass is upper bounded by a known positive constant. This assumption alleviates the definition of our distance below, since it does not require to treat separately the cases where either
such that their total mass is upper bounded by a known positive constant. This assumption alleviates the definition of our distance below, since it does not require to treat separately the cases where either 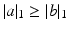 or
or 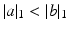 when comparing
when comparing 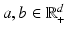 . Note also that this assumption always holds when dealing with finite collections of data. Without loss of generality, this is equivalent to considering vectors a in
. Note also that this assumption always holds when dealing with finite collections of data. Without loss of generality, this is equivalent to considering vectors a in 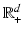 such that
such that 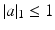 with a simple rescaling of all vectors by that constant. We define next the Kantorovich metric on
with a simple rescaling of all vectors by that constant. We define next the Kantorovich metric on 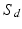 , where
, where 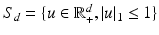 .
.Definition 1
(Kantorovich Distances on 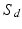 ). Let
). Let 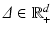 such that
such that 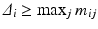 and
and 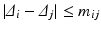 . Let
. Let 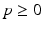 . For two elements a and b of
. For two elements a and b of 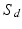 , we write
, we write 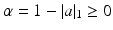 and
and 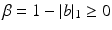 . Their p-Kantorovich distance raised to the power p is
. Their p-Kantorovich distance raised to the power p is
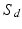 ). Let
). Let 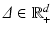 such that
such that 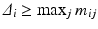 and
and 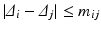 . Let
. Let 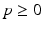 . For two elements a and b of
. For two elements a and b of 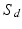 , we write
, we write 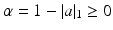 and
and 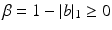 . Their p-Kantorovich distance raised to the power p is
. Their p-Kantorovich distance raised to the power p is
![$$\begin{aligned} K^p_{p \varDelta }(a,b)= \mathbf {OT}\left( \left[ {\begin{matrix}a\\ \alpha \end{matrix}}\right] ,\left[ {\begin{matrix}b\\ \beta \end{matrix}}\right] ,\hat{M}^p\right) , \text { where } \hat{M}=\begin{bmatrix}M&\varDelta \\\varDelta ^T&0\end{bmatrix}\in \mathbb {R}_+^{d+1\times d+1}.\end{aligned}$$](/wp-content/uploads/2016/09/A339424_1_En_20_Chapter_Equ3.gif)