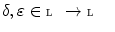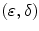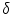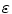as arranging the elements of 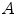 in a line. Not surprisingly, the task of defining a total order for a given set depends greatly on the prior knowledge provided. To illustrate this point, imagine a scenario where two researchers want to order a set of people. The first one defines minimum as the youngest person and the maximum as the oldest person, the second declares the minimum as the fattest one and the maximum as the thinnest one. Clearly, two persons that are similar according to the first researcher’s setting might be dissimilar according to the second’s. Accordingly, the complete list of ordered people can be totally different from one researcher to another.In the field of image processing, the definition of a total ordering among pixels of the image is the main ingredient of mathematical morphology techniques [20]. In this first part of this chapter, we study the case where “prior” knowledge about the spectral information of the background and the foreground on the image is available. We define a supervised ordering as a particular case of reduced ordering where the minimum (resp. maximum) value should be a pixel in the background (resp. foreground). This restriction can be included in the computation of the supervised ordering by using classical machine learning techniques, for instance, by support vector machines (SVM) [25]. Another possibility for known structure in the total ordering problem is to assume that the image is composed by two main components: background and foreground. Additionally, we include the assumption that the background is larger than the foreground. We uncover an interesting application of randomised approximation schemes in multivariate analysis [26]. To summarise, in this chapter a multispectral image is represented through a total ordering and it is analysed by mathematical morphology transformations. Prior information about the spectral information in the image is incorporated into the workflow of mathematical morphology transformations in two scenarios:
in a line. Not surprisingly, the task of defining a total order for a given set depends greatly on the prior knowledge provided. To illustrate this point, imagine a scenario where two researchers want to order a set of people. The first one defines minimum as the youngest person and the maximum as the oldest person, the second declares the minimum as the fattest one and the maximum as the thinnest one. Clearly, two persons that are similar according to the first researcher’s setting might be dissimilar according to the second’s. Accordingly, the complete list of ordered people can be totally different from one researcher to another.In the field of image processing, the definition of a total ordering among pixels of the image is the main ingredient of mathematical morphology techniques [20]. In this first part of this chapter, we study the case where “prior” knowledge about the spectral information of the background and the foreground on the image is available. We define a supervised ordering as a particular case of reduced ordering where the minimum (resp. maximum) value should be a pixel in the background (resp. foreground). This restriction can be included in the computation of the supervised ordering by using classical machine learning techniques, for instance, by support vector machines (SVM) [25]. Another possibility for known structure in the total ordering problem is to assume that the image is composed by two main components: background and foreground. Additionally, we include the assumption that the background is larger than the foreground. We uncover an interesting application of randomised approximation schemes in multivariate analysis [26]. To summarise, in this chapter a multispectral image is represented through a total ordering and it is analysed by mathematical morphology transformations. Prior information about the spectral information in the image is incorporated into the workflow of mathematical morphology transformations in two scenarios:
2 Complete Lattices and Mathematical Morphology
2.1 Mathematical Morphology
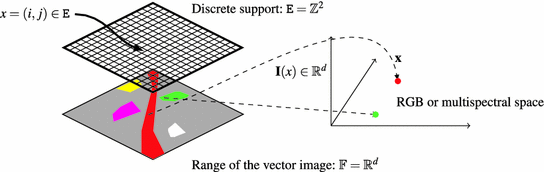
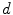 -variate image,
-variate image, 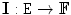 . Note that the image
. Note that the image 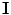 maps each spatial point
maps each spatial point 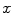 to a vector
to a vector 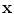 in three dimension for a RGB image or in dimension
in three dimension for a RGB image or in dimension 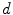 for the case of a multispectral image
for the case of a multispectral image2.2 Fundamental Definitions
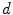 -dimensional image (denoted by
-dimensional image (denoted by 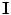 ) which maps the spatial support
) which maps the spatial support 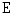 to the vector support
to the vector support 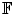 , i.e.,
, i.e.,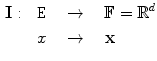
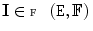 , i.e. is a mapping from the spatial support to the vector space of dimensions
, i.e. is a mapping from the spatial support to the vector space of dimensions 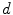 . Theoretical formulation of mathematical morphology is nowadays phrased in terms of complete lattices and operators defined on them. For a detailed exposition on complete lattice theory in mathematical morphology, we refer to J. Serra and C. Ronse in [16, Chap. 2].
. Theoretical formulation of mathematical morphology is nowadays phrased in terms of complete lattices and operators defined on them. For a detailed exposition on complete lattice theory in mathematical morphology, we refer to J. Serra and C. Ronse in [16, Chap. 2].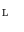 endowed with a partial order
endowed with a partial order 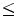 is called a complete lattice, denoted
is called a complete lattice, denoted 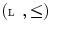 if every subset
if every subset 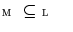 has both supremum (join)
has both supremum (join) 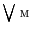 and infimum (meet)
and infimum (meet) 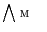 .
.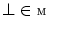 is an element which is least than or equal to any other element of
is an element which is least than or equal to any other element of 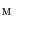 , that is,
, that is, 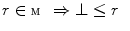 . We denote the minimum of
. We denote the minimum of 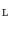 by
by 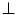 . Equivalently, a maximum (largest)
. Equivalently, a maximum (largest) 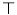 in
in 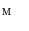 is the greatest element of
is the greatest element of 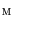 , that is,
, that is, 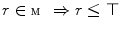 . We denote the maximum of
. We denote the maximum of 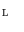 by
by 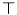 .
.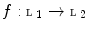 of a complete lattice
of a complete lattice 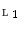 into a complete lattice
into a complete lattice 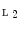 is said to be a dilation if
is said to be a dilation if 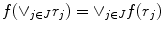 for all families
for all families 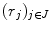 of elements in
of elements in 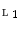 . A mapping is said to be an erosion if
. A mapping is said to be an erosion if 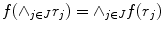 for all families
for all families 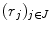 of elements in
of elements in 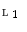 .
.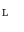 , we always have a dual isomorphism between the complete lattice of dilation on
, we always have a dual isomorphism between the complete lattice of dilation on 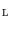 and the complete lattice of erosions on
and the complete lattice of erosions on 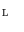 . This dual isomorphism is called by Serra [20, Chap. 1] the morphological duality. In fact it is linked to what one calls Galois connections in lattice theory, as we will see at the end of this section.
. This dual isomorphism is called by Serra [20, Chap. 1] the morphological duality. In fact it is linked to what one calls Galois connections in lattice theory, as we will see at the end of this section.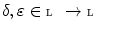 . Then we say that
. Then we say that 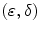 is an adjunction of every
is an adjunction of every 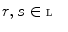 , we have
, we have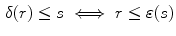
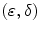 ,
, 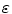 is called the upper adjoint and
is called the upper adjoint and 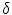 the lower adjoint.
the lower adjoint. and
and 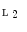 be lattices and let
be lattices and let 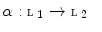 and
and 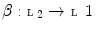 satisfy the following conditions.
satisfy the following conditions.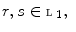 if
if 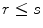 , then
, then 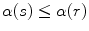 .
.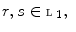 if
if 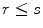 , then
, then 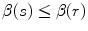 .
.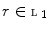 ,
, 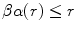 .
.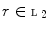 ,
, 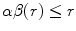 .
.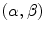 is a Galois connection between
is a Galois connection between 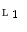 and
and 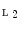 .
.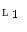 and
and 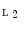 , maps
, maps 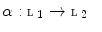 and
and 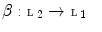 a Galois connection. Then the following condition holds for all
a Galois connection. Then the following condition holds for all 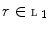 and
and 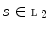 :
: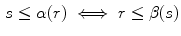
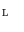 is a Galois connection between the dual
is a Galois connection between the dual 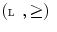 and
and 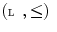 (indeed, compare Definition 3 and Proposition 2).
(indeed, compare Definition 3 and Proposition 2).2.3 Preorder by 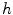 -Function
-Function
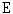 be a nonempty set and assume that
be a nonempty set and assume that 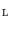 is a complete lattice. Let
is a complete lattice. Let 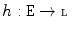 be a surjective mapping. Define an equivalence relation
be a surjective mapping. Define an equivalence relation 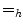 on
on 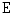 as follows:
as follows: 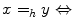
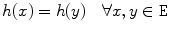 . As it was defined in [8], we refer by
. As it was defined in [8], we refer by 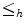 the
the 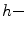 ordering given by the following relation on
ordering given by the following relation on 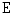
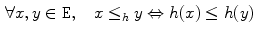
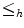 preserves reflexivity (
preserves reflexivity (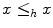 ) and transitivity (
) and transitivity (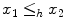 and
and 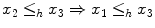 ). However,
). However, 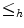 is not a partial ordering because
is not a partial ordering because 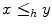 and
and 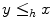 implies only that
implies only that 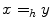 but not
but not 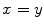 . Note that
. Note that 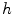 -ordering is a preorder in
-ordering is a preorder in 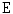 .
.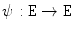 is
is 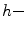 increasing if
increasing if 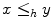 implies that
implies that 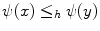 . Additionally, since
. Additionally, since 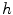 is surjective, an equivalence class is defined by
is surjective, an equivalence class is defined by ![$${\fancyscript{L}}[r]=\{y\in {\mathtt {E}}| h(y) = r\}$$](/wp-content/uploads/2016/03/A308467_1_En_7_Chapter_IEq107.gif) . The Axiom of Choice [8] implies that there exist mappings
. The Axiom of Choice [8] implies that there exist mappings 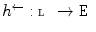 such that
such that 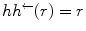 , for
, for 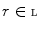 . Unless
. Unless 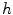 is injective, there exist more than one such
is injective, there exist more than one such 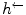 mappings:
mappings: 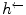 is called the semi-inverse of
is called the semi-inverse of 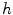 . Note that
. Note that 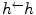 is not the identity mapping in general (but
is not the identity mapping in general (but 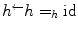 ). However, we have that for any
). However, we have that for any 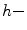 increasing
increasing 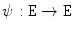 the result
the result 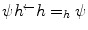 and hence
and hence 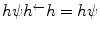 . Let us introduce
. Let us introduce 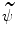 the operator associated to
the operator associated to 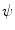 in the lattice
in the lattice 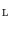 . A mapping
. A mapping 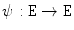 is
is 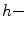 increasing if and only if there exists an increasing mapping
increasing if and only if there exists an increasing mapping 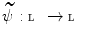 such that
such that 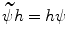 . The mapping
. The mapping 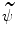 is uniquely determined by
is uniquely determined by 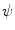 and can be computed from
and can be computed from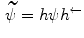
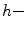 erosion and
erosion and 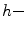 dilation. Let
dilation. Let 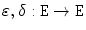 be two mappings with the property
be two mappings with the property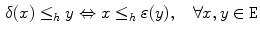
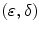 is called an
is called an 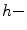 adjunction. Moreover, let
adjunction. Moreover, let 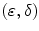 be
be 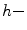 increasing mappings on
increasing mappings on 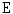 , and let
, and let 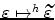 ,
, 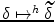 . Then
. Then 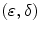 is an
is an 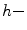 adjunction on
adjunction on 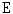 if and only if
if and only if 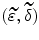 is an adjunction on the lattice
is an adjunction on the lattice 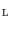 . Therefore a mapping
. Therefore a mapping 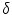 (resp.
(resp. 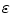 ) on
) on 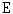 is called
is called 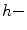 dilation (resp.
dilation (resp. 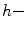 erosion) if
erosion) if 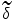 (resp.
(resp. 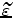 ) is a dilation (resp. erosion) on
) is a dilation (resp. erosion) on 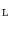 .
. 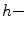 adjunctions inherit a large number of properties from ordinary adjunctions between complete lattices. Assume that
adjunctions inherit a large number of properties from ordinary adjunctions between complete lattices. Assume that 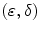 is an
is an 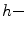
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree