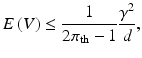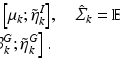(1)
where β is the d × q regression coefficient matrix. The optimal β obtained by solving (1) is equivalent to regressing each column of Y on X independently. Thus, the relations between columns of Y are ignored. To incorporate this information in estimating β, one of the state-of-the-art approaches is to employ the SMR model [2]:
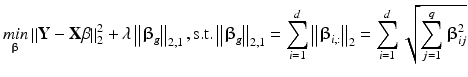
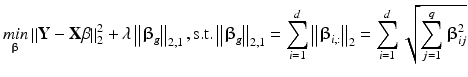
(2)
where ||β g ||2,1 is the group LASSO penalty and each row of β, denoted as β i,:, corresponds to a feature. With elements of each β i,: taken as a group, only features associated with all q response variables would be selected with the corresponding β i,j ≠ 0 for all j. To set λ, we search over 100 λ’s in [λ max, λ min], where 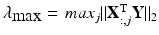 and
and 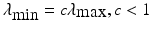 . Optimal λ is defined as the one that minimizes the prediction error over 1000 subsamples with the data randomly split into 80 % for model training and 20 % for error evaluation. A fast solver of (2) can be solved with GLMNET [13].
. Optimal λ is defined as the one that minimizes the prediction error over 1000 subsamples with the data randomly split into 80 % for model training and 20 % for error evaluation. A fast solver of (2) can be solved with GLMNET [13].
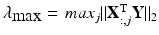 and
and 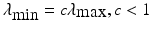 . Optimal λ is defined as the one that minimizes the prediction error over 1000 subsamples with the data randomly split into 80 % for model training and 20 % for error evaluation. A fast solver of (2) can be solved with GLMNET [13].
. Optimal λ is defined as the one that minimizes the prediction error over 1000 subsamples with the data randomly split into 80 % for model training and 20 % for error evaluation. A fast solver of (2) can be solved with GLMNET [13].2.2 Stability Selection
A problem with assuming features associated with nonzero β i,: in SMR are all relevant is that this property is true only under very restricted conditions, which are largely violated in most real applications [3]. In particular, this guarantee on correct feature selection does not hold when features are highly correlated, which is often the case for real data [3]. With correlated features, perturbations to the data can result in drastic changes in the features that are selected. Based on this observation, an intuitive approach to deal with correlated features is to perturb the data and declare features that are consistently selected over different perturbations as relevant, which is the basis of SS. We describe here SS in the case of SMR, but SS can generally be applied to any models that are equipped with a feature selection mechanism. Given X, Y, and [λ max, λ min], SS combined with Randomized LASSO proceeds as follows [9]:
1.
Multiply each column of X by 0.5 or 1 selected at random.
2.
Randomly subsample X and Y by half to generate X s and Y s .
3.
For each λ in [λ max, λ min], apply SMR to generate β s (λ). Let S s (λ) be a d ×1 vector with elements corresponding to selected features, i.e. nonzero β s (λ), set to 1.
4.
Repeat steps 2 and 3 S times, e.g. with S = 1000.
5.
Compute the proportion of subsamples, π i (λ), that each feature i is selected for each λ in [λ max, λ min].
6.
Declare feature i as significant if max λ π i (λ) > π th.
where V is the number of false positives and γ is the expected number of selected features, which can be approximated by: 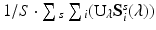 . U λ denotes the union over λ. We highlight two insights on (3) that have major implications on applying SS in practice. First, (3) is a conservative bound on the family-wise error rate (FWER) =P(V ≥ 1), since
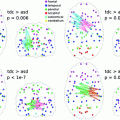
. U λ denotes the union over λ. We highlight two insights on (3) that have major implications on applying SS in practice. First, (3) is a conservative bound on the family-wise error rate (FWER) =P(V ≥ 1), since ![$$ E(V) = \sum {_{v = 1} }^{\infty } P(V \ge v) > P(V \ge 1) $$” src=”/wp-content/uploads/2016/09/A339424_1_En_9_Chapter_IEq4.gif”></SPAN> . To control FWER at <SPAN class=EmphasisTypeItalic>α</SPAN> = 0.05 with multiple comparison correction (MCC), i.e. <SPAN class=EmphasisTypeItalic>P</SPAN>(<SPAN class=EmphasisTypeItalic>V</SPAN> ≥ 1) ≤ <SPAN class=EmphasisTypeItalic>α</SPAN>/<SPAN class=EmphasisTypeItalic>d</SPAN>, even for <SPAN class=EmphasisTypeItalic>γ</SPAN> = 1, <SPAN class=EmphasisTypeItalic>π</SPAN> <SUB>th</SUB> based on (<SPAN class=InternalRef><A href=]() 3) is >1. Since π i (λ) ϵ [0,1], π th should be clipped at 1, but whether FWER is still controlled is unclear. Second, a key property of SS is that it does not require choosing a specific λ. However, for n/2 > d, a “small enough” λ min could lead to all features being selected in all subsamples, resulting in max λ π i (λ) = 1. Hence, all features would be declared as significant. λ selection is thus translated into λ min selection, which warrants caution. An example from real data (Sect. 3.2) illustrating the impact of λ min and π th is shown in Fig. 1(a). Even with λ min set to 0.1, i.e. a λ range that would strongly encourage sparsity, a π th of 0.9 (strictest π th in the suggested range of [0.6, 0.9] in [9]) declares >40 % of the features as significant, i.e. fails to control for false positives.
3) is >1. Since π i (λ) ϵ [0,1], π th should be clipped at 1, but whether FWER is still controlled is unclear. Second, a key property of SS is that it does not require choosing a specific λ. However, for n/2 > d, a “small enough” λ min could lead to all features being selected in all subsamples, resulting in max λ π i (λ) = 1. Hence, all features would be declared as significant. λ selection is thus translated into λ min selection, which warrants caution. An example from real data (Sect. 3.2) illustrating the impact of λ min and π th is shown in Fig. 1(a). Even with λ min set to 0.1, i.e. a λ range that would strongly encourage sparsity, a π th of 0.9 (strictest π th in the suggested range of [0.6, 0.9] in [9]) declares >40 % of the features as significant, i.e. fails to control for false positives.

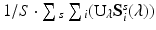 . U λ denotes the union over λ. We highlight two insights on (3) that have major implications on applying SS in practice. First, (3) is a conservative bound on the family-wise error rate (FWER) =P(V ≥ 1), since
. U λ denotes the union over λ. We highlight two insights on (3) that have major implications on applying SS in practice. First, (3) is a conservative bound on the family-wise error rate (FWER) =P(V ≥ 1), since 
Fig. 1.
Behavior of SS and BPT on real data. (a) π i (λ) at λ = 0.1 (for SS). (b) Gaussian fit on Studentized statistics (for BPT). (c) Gumbel fit on maxima of Studentized statistics (for BPT).
2.3 Bootstrapped Permutation Testing
For models with unknown parameter distribution, including those with no intrinsic feature selection mechanisms, PT is often used to perform statistical inference. PT involves permuting responses a large number of times (e.g. 10000 in this work) and relearning the model parameters for each permutation in generating null distributions of the parameters. Features with original parameter values greater than (or less than) a certain percentile of the null, e.g. >100∙(1‒0.025/d)th percentile (or <100∙(0.025/d)th percentile), are declared as significant. Equivalently, one can count the number of permutations with parameter values exceeding/below the original parameter values to generate approximate p-values. A key attribute of PT is that it does not impose any distributional assumptions on the parameters, but the cost of this flexibility is the need for a large number of permutations to ensure the resolution of the approximate p-values are fine enough for proper statistical testing, i.e. the smallest p-value attainable from N permutation is 1/N. Also, if the underlying parameter distribution is known, the associated parametric test is statistically more powerful [12].
The central idea behind BPT is to generate Studentized statistics via bootstrapping to exploit how the variability of the parameter estimates associated with relevant features are likely higher with responses permuted. Similar to PT, BPT can be applied to any models. We describe here BPT in the context of SMR, which proceeds as follows.
Estimation of Studentized statistics, 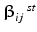 :
:
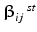 :
:1.
Bootstrap X and Y with replacement for B = 1000 times, and denote the bootstrap samples as X b and Y b .
2.
Multiply each column of X b by 0.5 or 1 selected at random.
3.
Select the optimal λ for SMR by repeated random subsampling on X and Y, and apply SMR on X b and Y b for each bootstrap b with this λ to estimate β b .
4.
Compute Studentized statistics, 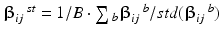 where
where 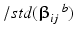 is the standard deviation over bootstrap samples.
is the standard deviation over bootstrap samples.
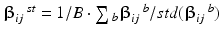 where
where 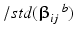 is the standard deviation over bootstrap samples.
is the standard deviation over bootstrap samples.Estimation of the null distribution of 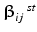 :
:
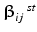 :
:5.
Permute Y for N = 500 times.
6.
For each permutation k, compute 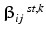 with the same λ, samples, and feature weighting used in each bootstrap b as in the non-permuted case.
with the same λ, samples, and feature weighting used in each bootstrap b as in the non-permuted case.
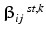 with the same λ, samples, and feature weighting used in each bootstrap b as in the non-permuted case.
with the same λ, samples, and feature weighting used in each bootstrap b as in the non-permuted case.7.
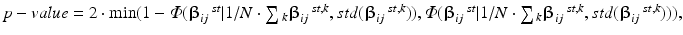 where Ф(∙) = the normal cumulative distribution function.
where Ф(∙) = the normal cumulative distribution function.




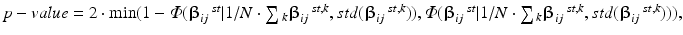 where Ф(∙) = the normal cumulative distribution function.
where Ф(∙) = the normal cumulative distribution function.Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree