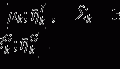between two points i and j in the image domain, defined by
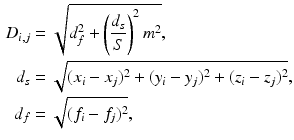
(1)
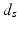 is the spatial Euclidean distance,
is the spatial Euclidean distance, 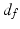 is the image intensity similarity, and these two different measures are combined into a single one with
is the image intensity similarity, and these two different measures are combined into a single one with 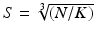 (N the number of voxels and K the number of supervoxels) being the mean spatial distance within a supervoxel as a normalisation factor, and m being a weight between the intensity similarity and spatial proximity. Note that the intensity similarity
(N the number of voxels and K the number of supervoxels) being the mean spatial distance within a supervoxel as a normalisation factor, and m being a weight between the intensity similarity and spatial proximity. Note that the intensity similarity 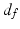 can be extended to include additional dimensions when there are a group of images or multi-channel information for clustering.
can be extended to include additional dimensions when there are a group of images or multi-channel information for clustering.It can be seen that SLIC does not explicitly enforce connectivity, therefore in this work, connected-component labelling [16] was performed after SLIC supervoxel clustering to assign the originally disconnected groups of voxels within the same supervoxel to new supervoxels where all the voxels within the same supervoxel are spatially connected. Also the supervoxels generated by SLIC of extremely small size due to image noise were considered as “orphans” and were merged into the nearest supervoxels.
The over-segmentation generated by the supervoxel clustering leads to a sparse image representation when the number of supervoxels K is greatly smaller than the number of voxels N. Let 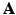 denote the representation matrix in the image domain,
denote the representation matrix in the image domain, 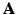 is binary and sparse, which determines whether a voxel i belongs to a given supervoxel j, that is
is binary and sparse, which determines whether a voxel i belongs to a given supervoxel j, that is
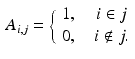 Then from the supervoxel intensity values
Then from the supervoxel intensity values 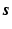 , the original image
, the original image 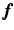 on the voxel grid can be established by
on the voxel grid can be established by 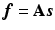 where
where 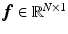 and
and 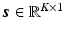 . In PET reconstruction, using the image representation
. In PET reconstruction, using the image representation 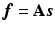 with a given
with a given 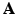 (not a square matrix) transfers the reconstruction of the original image
(not a square matrix) transfers the reconstruction of the original image 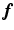 to the estimation of
to the estimation of 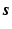 with less number of the unknowns when
with less number of the unknowns when 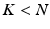 , without losing the image details preserved in
, without losing the image details preserved in 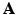 . The joint determination of
. The joint determination of 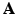 from both the anatomical prior images and the PET data will be discussed in Sect. 2.3. Notably, in contrary to embedding the anatomical information within a Bayesian reconstruction framework based on solely the image intensity such as joint entropy or mutual information, the proposed method avoids the potential bias by using the image geometry instead.
from both the anatomical prior images and the PET data will be discussed in Sect. 2.3. Notably, in contrary to embedding the anatomical information within a Bayesian reconstruction framework based on solely the image intensity such as joint entropy or mutual information, the proposed method avoids the potential bias by using the image geometry instead.
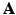 denote the representation matrix in the image domain,
denote the representation matrix in the image domain, 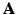 is binary and sparse, which determines whether a voxel i belongs to a given supervoxel j, that is
is binary and sparse, which determines whether a voxel i belongs to a given supervoxel j, that is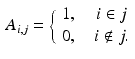
 , the original image
, the original image  on the voxel grid can be established by
on the voxel grid can be established by 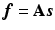 where
where 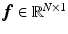 and
and 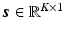 . In PET reconstruction, using the image representation
. In PET reconstruction, using the image representation 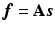 with a given
with a given 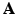 (not a square matrix) transfers the reconstruction of the original image
(not a square matrix) transfers the reconstruction of the original image 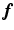 to the estimation of
to the estimation of 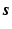 with less number of the unknowns when
with less number of the unknowns when 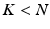 , without losing the image details preserved in
, without losing the image details preserved in 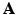 . The joint determination of
. The joint determination of 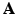 from both the anatomical prior images and the PET data will be discussed in Sect. 2.3. Notably, in contrary to embedding the anatomical information within a Bayesian reconstruction framework based on solely the image intensity such as joint entropy or mutual information, the proposed method avoids the potential bias by using the image geometry instead.
from both the anatomical prior images and the PET data will be discussed in Sect. 2.3. Notably, in contrary to embedding the anatomical information within a Bayesian reconstruction framework based on solely the image intensity such as joint entropy or mutual information, the proposed method avoids the potential bias by using the image geometry instead.2.2 PET Reconstruction with Sparse Image Representation
The sparse image representation can be directly integrated into the forward model of PET reconstruction
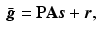
where 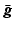 is the expected projection data,
is the expected projection data, 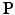 is the system information matrix of the detection probabilities, and
is the system information matrix of the detection probabilities, and 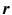 is the expected scatter and random events.
is the expected scatter and random events.
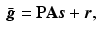
(2)
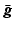 is the expected projection data,
is the expected projection data, 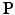 is the system information matrix of the detection probabilities, and
is the system information matrix of the detection probabilities, and 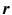 is the expected scatter and random events.
is the expected scatter and random events.Within the maximum likelihood (ML) reconstruction framework, the estimate of the image 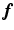 (here
(here 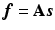 ) is found by maximising the Poisson log likelihood [17]
) is found by maximising the Poisson log likelihood [17]
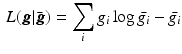
with observed projection data 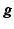
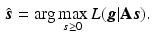
The iterative update to find the solution can be directly derived by the expectation-maximisation (EM) algorithm [8]
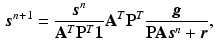
where T denotes the matrix transpose and n denotes the iteration number.
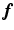 (here
(here 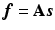 ) is found by maximising the Poisson log likelihood [17]
) is found by maximising the Poisson log likelihood [17]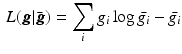
(3)
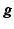
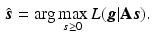
(4)
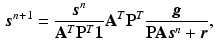
(5)
With prior images, it is possible to have the sparse image representation matrix 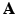 defined on a denser voxel grid that does not match the PET imaging system characterised by
defined on a denser voxel grid that does not match the PET imaging system characterised by 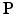 . Instead of downsampling the prior images to match the PET imaging resolution, in this work a resampling operator is introduced into the forward model to maintain the image at higher spatial resolution to avoid the loss of the edges and other image details. Let
. Instead of downsampling the prior images to match the PET imaging resolution, in this work a resampling operator is introduced into the forward model to maintain the image at higher spatial resolution to avoid the loss of the edges and other image details. Let 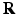 denote the matrix form of the resampling operator in the image domain, then the forward model becomes
denote the matrix form of the resampling operator in the image domain, then the forward model becomes  , and the iterative update becomes
, and the iterative update becomes
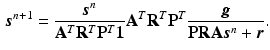
So far it has been demonstrated the use of the sparse image representation in reconstructing PET images. For dynamic PET data, directly reconstruct the parametric images from the raw projection data can achieve improved accuracy and robustness [9, 18, 19]. The sparse image representation is directly applicable to dynamic PET data as it is a linear operation in the image domain. For dynamic PET data, the sparse representation matrix 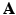 is consistent for all time frames, and in
is consistent for all time frames, and in 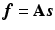 ,
, 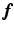 and
and 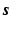 are expanded so that
are expanded so that 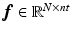 and
and 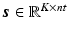 where nt is the number of time frames. Using a linearised kinetic model [20],
where nt is the number of time frames. Using a linearised kinetic model [20], 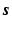 can be described as
can be described as 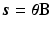 , where
, where 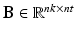 are the temporal basis functions and
are the temporal basis functions and 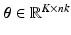 are the kinetic parameters for all supervoxels, with nk being the number of kinetic parameters for each supervoxel. The direct estimation of the kinetic parameters
are the kinetic parameters for all supervoxels, with nk being the number of kinetic parameters for each supervoxel. The direct estimation of the kinetic parameters 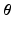 can be solved by applying the optimisation transfer technique [9] to obtain a closed-form update equation with improved convergence performance.
can be solved by applying the optimisation transfer technique [9] to obtain a closed-form update equation with improved convergence performance.
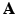 defined on a denser voxel grid that does not match the PET imaging system characterised by
defined on a denser voxel grid that does not match the PET imaging system characterised by 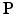 . Instead of downsampling the prior images to match the PET imaging resolution, in this work a resampling operator is introduced into the forward model to maintain the image at higher spatial resolution to avoid the loss of the edges and other image details. Let
. Instead of downsampling the prior images to match the PET imaging resolution, in this work a resampling operator is introduced into the forward model to maintain the image at higher spatial resolution to avoid the loss of the edges and other image details. Let 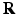 denote the matrix form of the resampling operator in the image domain, then the forward model becomes
denote the matrix form of the resampling operator in the image domain, then the forward model becomes  , and the iterative update becomes
, and the iterative update becomes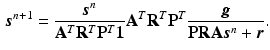
(6)
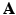 is consistent for all time frames, and in
is consistent for all time frames, and in 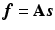 ,
, 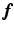 and
and 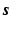 are expanded so that
are expanded so that 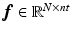 and
and 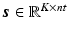 where nt is the number of time frames. Using a linearised kinetic model [20],
where nt is the number of time frames. Using a linearised kinetic model [20], 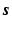 can be described as
can be described as 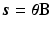 , where
, where 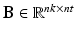 are the temporal basis functions and
are the temporal basis functions and 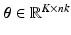 are the kinetic parameters for all supervoxels, with nk being the number of kinetic parameters for each supervoxel. The direct estimation of the kinetic parameters
are the kinetic parameters for all supervoxels, with nk being the number of kinetic parameters for each supervoxel. The direct estimation of the kinetic parameters 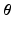 can be solved by applying the optimisation transfer technique [9] to obtain a closed-form update equation with improved convergence performance.
can be solved by applying the optimisation transfer technique [9] to obtain a closed-form update equation with improved convergence performance.2.3 Aggregation of Multi-layer Supervoxels and Joint Clustering
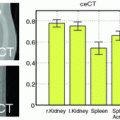
A single layer of supervoxels provides a sparse representation of the image which is affected by the algorithm and parameters used to generated the over-segmentation. As suggested in [21], aggregation of multi-layer supervoxels generated by different algorithms with varying parameters can improve the performance of capturing the diverse and multi-scale visual features in a natural image. For PET reconstruction, to eliminate the bias introduced by a specific algorithm or parameter, the aggregation can be performed as an average of multiple PET images reconstructed from the same projection data and prior images using different over-segmentations generated by varying the supervoxel clustering algorithm and/or the parameters. In this work the multi-layer supervoxels were generated by varying the number of supervoxels N and the weight m between the intensity similarity and spatial proximity in the SLIC algorithm.
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree