different system functions, 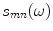 and acoustic/elastic transfer functions,
and acoustic/elastic transfer functions, 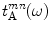 that generate the received voltages,
that generate the received voltages, 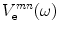 , where
, where

(10.1)
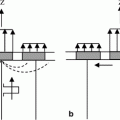
Equation (10.1) can be used to obtain these system functions experimentally if we measure the received voltages in a calibration setup and have explicit models for the acoustic/elastic transfer functions in that setup. The calibration setups we will use for immersion and contact tests are shown in Fig. 10.1, where a 2-D or linear array is placed parallel to a plane reflecting interface and the reflection of the waves generated by driving a single element of the array is received by a single receiving element. A more detailed description of the setup geometry is shown in Fig. 10.2 for a pair of sending and receiving rectangular elements.
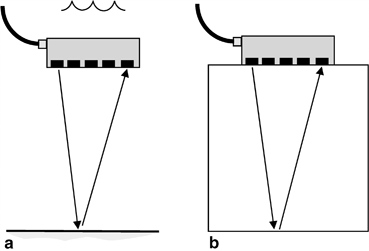
Fig. 10.1
Calibration setups for obtaining the system functions a for an immersion test, and b for a contact test
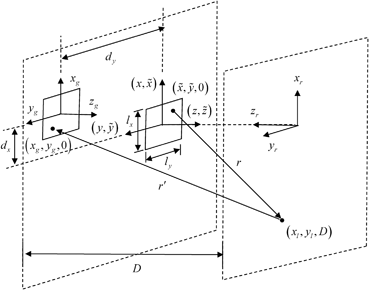
Fig. 10.2
A calibration setup geometry involving two rectangular array elements and a parallel plane reflecting interface
Consider first an immersion setup. Our starting point in this case is the Rayleigh-Sommerfeld model for an element, Eq. (6.21), where the velocity is assumed to be constant over the face of the driving element, i.e. we will use a piston model . The pressure due to the waves generated by the driving element at a point 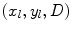 in the fluid at the location of the reflecting interface is given as
in the fluid at the location of the reflecting interface is given as
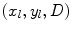 in the fluid at the location of the reflecting interface is given as
in the fluid at the location of the reflecting interface is given as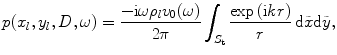
(10.2)
where 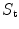 is the area of the transmitting element, the distance from a point
is the area of the transmitting element, the distance from a point 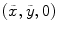 on the sending element to a point
on the sending element to a point 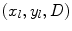 on the reflecting interface is
on the reflecting interface is 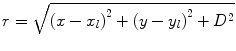 ,
, 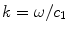 is the wave number for the fluid, and
is the wave number for the fluid, and 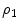 is the density of the fluid. If we assume the reflector is far enough away from the element so that
is the density of the fluid. If we assume the reflector is far enough away from the element so that 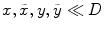 then we can approximate this distance as
then we can approximate this distance as ![$$r\cong D+\left[ {{(\tilde{x}-{{x}_{l}})}^{2}}+{{(\tilde{y}-{{y}_{l}})}^{2}} \right]/2D$$](/wp-content/uploads/2016/05/A314073_1_En_10_Chapter_IEq13.gif) (paraxial approximation) and we find
(paraxial approximation) and we find
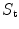 is the area of the transmitting element, the distance from a point
is the area of the transmitting element, the distance from a point 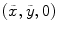 on the sending element to a point
on the sending element to a point 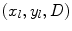 on the reflecting interface is
on the reflecting interface is 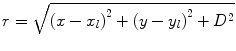 ,
, 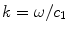 is the wave number for the fluid, and
is the wave number for the fluid, and 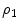 is the density of the fluid. If we assume the reflector is far enough away from the element so that
is the density of the fluid. If we assume the reflector is far enough away from the element so that 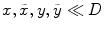 then we can approximate this distance as
then we can approximate this distance as ![$$r\cong D+\left[ {{(\tilde{x}-{{x}_{l}})}^{2}}+{{(\tilde{y}-{{y}_{l}})}^{2}} \right]/2D$$](/wp-content/uploads/2016/05/A314073_1_En_10_Chapter_IEq13.gif) (paraxial approximation) and we find
(paraxial approximation) and we find![$$p({{x}_{\text{l}}},{{y}_{\text{l}}},D,\omega )=\frac{-\text{i}\omega {{\rho }_{1}}{{v}_{0}}(\omega )\exp (\text{i}kD)}{2\text{ }\!\!\pi\!\!\text{ }D}\int_{{{S}_{\text{t}}}}{\left[ \text{i}k\frac{{{(\tilde{x}-{{x}_{\text{l}}})}^{2}}+{{(\tilde{y}-{{y}_{\text{l}}})}^{2}}}{2D} \right]}\,\text{d}\tilde{x}\,\text{d}\tilde{y}.$$](/wp-content/uploads/2016/05/A314073_1_En_10_Chapter_Equ3.gif)
(10.3)
If we assume we can treat the interactions of these incident waves with the reflecting interface as a quasi-plane wave interaction at normal incidence, then pressure in the reflected wave at the interface, 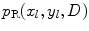 , is
, is
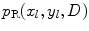 , is
, is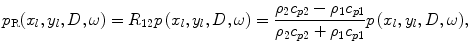
(10.4)
where 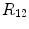 is the plane wave reflection coefficient at normal incidence (based on a pressure ratio) and
is the plane wave reflection coefficient at normal incidence (based on a pressure ratio) and 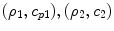 are the density and compressional wave speed for the fluid and reflecting solid, respectively. The normal velocity,
are the density and compressional wave speed for the fluid and reflecting solid, respectively. The normal velocity, 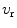 , at the interface in the
, at the interface in the 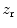 -direction (directed towards the receiving element, see Fig. 10.2) is also given by the plane wave relationship
-direction (directed towards the receiving element, see Fig. 10.2) is also given by the plane wave relationship
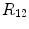 is the plane wave reflection coefficient at normal incidence (based on a pressure ratio) and
is the plane wave reflection coefficient at normal incidence (based on a pressure ratio) and 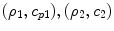 are the density and compressional wave speed for the fluid and reflecting solid, respectively. The normal velocity,
are the density and compressional wave speed for the fluid and reflecting solid, respectively. The normal velocity, 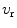 , at the interface in the
, at the interface in the 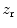 -direction (directed towards the receiving element, see Fig. 10.2) is also given by the plane wave relationship
-direction (directed towards the receiving element, see Fig. 10.2) is also given by the plane wave relationship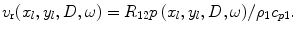
(10.5)
Using this velocity field as specified on the entire interface, we can again use the Rayleigh-Sommerfeld integral to obtain the pressure, 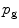 , of the reflected waves at a point
, of the reflected waves at a point 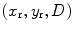 on the plane of the receiving element:
on the plane of the receiving element:
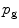 , of the reflected waves at a point
, of the reflected waves at a point 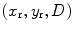 on the plane of the receiving element:
on the plane of the receiving element: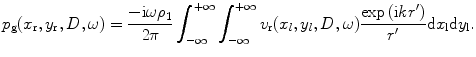
(10.6)
Applying the paraxial approximation to the distance 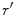 then gives
then gives
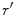 then gives
then gives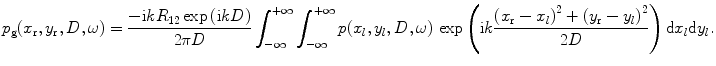
(10.7)
If the driving and receiving elements are separated by the distances 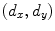 in the
in the 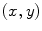 directions, respectively, then
directions, respectively, then
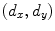 in the
in the 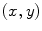 directions, respectively, then
directions, respectively, then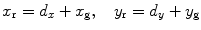
(10.8)
![$$ \begin{matrix} {{p}_{\text{g}}}({{x}_{\text{g}}},{{y}_{\text{g}}},D,\omega )=\frac{-\text{i}k{{R}_{12}}\exp \text{(i}kD)}{2\text{ }\!\!\pi\!\!\text{ }D}\int_{-\infty }^{+\infty }{\int_{-\infty }^{+\infty }{[p({{x}_{l}},{{y}_{l}},D,\omega )}}\\ \left. \exp \left( \text{i}k\frac{{{({{x}_{\text{g}}}+{{d}_{x}}-{{x}_{l}})}^{2}}+{{({{y}_{\text{g}}}+{{d}_{y}}-{{y}_{l}})}^{2}}}{2D} \right) \right]\text{d}{{x}_{l}}\text{d}{{y}_{l}}\\\end{matrix}. $$](/wp-content/uploads/2016/05/A314073_1_En_10_Chapter_Equ9.gif)
(10.9)
If we assume the incident wave interactions with the receiving transducer can be treated approximately as plane wave interactions, an assumption that is likely satisfied for the setup of Fig. 10.2, we can take the blocked force , 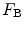 , at the receiving element to be simply twice the force exerted on the element by the incident waves [Schmerr-Song] and we have
, at the receiving element to be simply twice the force exerted on the element by the incident waves [Schmerr-Song] and we have
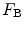 , at the receiving element to be simply twice the force exerted on the element by the incident waves [Schmerr-Song] and we have
, at the receiving element to be simply twice the force exerted on the element by the incident waves [Schmerr-Song] and we have![$$\begin{matrix}{{F}_{\text{B}}}(\omega )=2\int_{{{S}_{\text{r}}}}{{{p}_{\text{g}}}({{x}_{\text{g}}},{{y}_{\text{g}}},D,\omega )\,\text{d}{{x}_{\text{g}}}\text{d}{{y}_{\text{g}}}} \\=\frac{-2\text{i}k{{R}_{12}}\exp \,(\text{i}kD)}{2\text{ }\!\!\pi\!\!\text{ }D}\int_{{{S}_{\text{r}}}}{\left\{ \int_{-\infty }^{+\infty }{\int_{-\infty }^{+\infty }{\left[ p({{x}_{l}},{{y}_{l}},D,\omega ) \right.}} \right.} \\\left. \left. \exp \left( \text{i}k\frac{{{({{x}_{\text{g}}}+{{d}_{x}}-{{x}_{l}})}^{2}}+{{({{y}_{\text{g}}}+{{d}_{y}}-{{y}_{l}})}^{2}}}{2D} \right) \right]\text{d}{{x}_{l}}\text{d}{{y}_{l}} \right\}\text{d}{{x}_{\text{g}}}\text{d}{{y}_{\text{g}}} \\\end{matrix},$$](/wp-content/uploads/2016/05/A314073_1_En_10_Chapter_Equ10.gif)
(10.10)
where 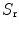 is the receiving area. Placing Eq. (10.3) into this result then gives
is the receiving area. Placing Eq. (10.3) into this result then gives
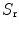 is the receiving area. Placing Eq. (10.3) into this result then gives
is the receiving area. Placing Eq. (10.3) into this result then gives![$$ \begin{aligned} {{F}_{\text{B}}}(\omega)&=\displaystyle\frac{-2\text{i}k{{R}_{12}}\exp (2\text{i}kD)}{2\text{ }\!\!\pi\!\!\text{ }D}\displaystyle\frac{-\text{i}k{{\rho}_{1}}{{c}_{p1}}{{v}_{0}}(\omega )}{2\text{ }\!\!\pi\!\!\text{ }D}\int_{{{S}_{\text{r}}}}\\ & \quad\;{\left[ \int_{-\infty }^{+\infty}{\int_{-\infty }^{+\infty } {\left[ \int_{{{S}_{\text{t}}}}{\left[\exp \left(\text{i}k\frac{{{(\tilde{x}-{{x}_{l}})}^{2}}+{{(\tilde{y}-{{y}_{l}})}^{2}}}{2D}\right) \right.} \right.}} \right.}\\ &\quad \left. \left. \left. \exp \left(\text{i}k\displaystyle\frac{{{({{x}_{\text{g}}}+{{d}_{x}}-{{x}_{l}})}^{2}}+{{({{y}_{\text{g}}}+{{d}_{y}}-{{y}_{l}})}^{2}}}{2D}\right) \right]\text{d}\tilde{x}\text{d}\tilde{y}\right]\text{d}{{x}_{l}}\text{d}{{y}_{l}}\right]\text{d}{{x}_{\text{g}}}\text{d}{{y}_{\text{g}}}. \end{aligned} $$](/wp-content/uploads/2016/05/A314073_1_En_10_Chapter_Equ11.gif)
(10.11)
Since the acoustic/elastic transfer function, 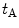 , for the immersion case is defined as
, for the immersion case is defined as 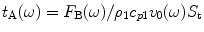 , this transfer function is
, this transfer function is
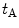 , for the immersion case is defined as
, for the immersion case is defined as 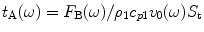 , this transfer function is
, this transfer function is![$$\begin{matrix}{{t}_{\text{A}}}(\omega )=2{{R}_{12}}{{\left[ \frac{-\text{i}k\exp \,(\text{i}kD)}{2\text{ }\!\!\pi\!\!\text{ }D} \right]}^{2}}\frac{1}{{{S}_{\text{t}}}}\int_{{{S}_{\text{r}}}}{\left[ \int_{-\infty }^{+\infty }{\int_{-\infty }^{+\infty }{\left[ \int_{{{S}_{\text{t}}}}{\left[ \exp \left( \text{i}k\frac{{{(\tilde{x}-{{x}_{l}})}^{2}}+{{(\tilde{y}-{{y}_{l}})}^{2}}}{2D} \right) \right.} \right.}} \right.} \\\left. \left. \left. \exp \left( \text{i}k\frac{{{({{x}_{\text{g}}}+{{d}_{x}}-{{x}_{l}})}^{2}}+{{({{y}_{\text{g}}}+{{d}_{y}}-{{y}_{l}})}^{2}}}{2D} \right) \right]\text{d}\tilde{x}\text{d}\tilde{y} \right]\text{d}{{x}_{l}}\text{d}{{y}_{l}} \right]\text{d}{{x}_{\text{g}}}\text{d}{{y}_{\text{g}}} \\\end{matrix}.$$](/wp-content/uploads/2016/05/A314073_1_En_10_Chapter_Equ12.gif)
(10.12)
Now, consider the integrals in Eq. (10.12) over the interface, i.e.
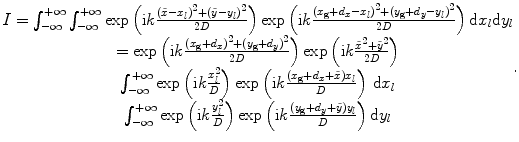
(10.13)
Both integrals appearing in Eq. (10.13) can be performed exactly since we have [Schmerr, Schmerr-Song]:
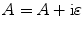 and then take the limit as
and then take the limit as 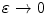 , the result is the same as using Eq. (10.14) directly on the forms given in Eq. (10.13) and we find
, the result is the same as using Eq. (10.14) directly on the forms given in Eq. (10.13) and we find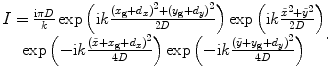
(10.15)
![$$\begin{array}{ll}{t_{\text{A}}}(\omega ) = 2{R_{12}}\frac{{ - {\text{i}}k\exp\;(2{\text{i}}kD)}}{{4{{\pi}}D{S_{\text{t}}}}}\int_{{S_{\text{r}}}}\left[{\int_{{S_{\text{t}}}} {\exp \left({{\text{i}}k\frac{{{{({x_{\text{g}}} + {d_x})}^2} +{{({y_{\text{g}}} + {d_y})}^2}}}{{2D}}} \right)\exp \left({{\text{i}}k\frac{{{{\tilde x}^2} + {{\tilde y}^2}}}{{2D}}}\right)} } \right.\\[8pt] \left. \exp \left( { - {\text{i}}k\frac{{{{(\tilde x +{x_{\text{g}}} + {d_x})}^2}}}{{4D}}} \right)\exp \left( { -{\text{i}}k\frac{{{{(\tilde y + {y_{\text{g}}} +{d_y})}^2}}}{{4D}}} \right){\text{d}}\tilde x{\text{d}}\tilde y\right]{\text{d}}{x_{\text{g}}}{\text{d}}{y_{\text{g}}}\end{array}.$$](/wp-content/uploads/2016/05/A314073_1_En_10_Chapter_Equ16.gif)
(10.16)
When the exponential terms in Eq. (10.16) are combined, this equation simplifies to
![$$\begin{matrix} {{t}_{\text{A}}}(\omega )=2{{R}_{12}}\frac{-\text{i}k\exp \,(2\text{i}kD)}{4\text{ }\!\!\pi\!\!\text{ }D{{S}_{\text{t}}}}\int_{{{S}_{\text{r}}}}{\left[ \int_{{{S}_{\text{t}}}}{\exp \left( \text{i}k\frac{{{[\tilde{x}-({{x}_{\text{g}}}+{{d}_{x}})]}^{2}}}{4D} \right)} \right.} \\ \left. \exp \left( \text{i}k\frac{{{[\tilde{y}-({{y}_{\text{g}}}+{{d}_{y}})]}^{2}}}{4D} \right)\text{d}\tilde{x}\text{d}\tilde{y} \right]\text{d}{{x}_{\text{g}}}\text{d}{{y}_{\text{g}}} \\ \end{matrix}.$$](/wp-content/uploads/2016/05/A314073_1_En_10_Chapter_Equ17.gif)
(10.17)
Since we are assuming that both the transmitting and receiving elements are of lengths 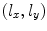 in the
in the 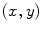 directions, respectively, Eq. (10.17) can be rewritten more explicitly as
directions, respectively, Eq. (10.17) can be rewritten more explicitly as
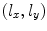 in the
in the 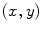 directions, respectively, Eq. (10.17) can be rewritten more explicitly as
directions, respectively, Eq. (10.17) can be rewritten more explicitly as![$$\begin{matrix} {{t}_{\text{A}}}(\omega )=2{{R}_{12}}\frac{-\text{i}k\exp (2\text{i}kD)}{4\text{ }\!\!\pi\!\!\text{ }D{{S}_{\text{t}}}}\left[ \int_{-{{l}_{x}}/2}^{{{l}_{x}}/2}{\int_{-{{l}_{x}}/2}^{{{l}_{x}}/2}{\exp \left( \text{i}k\frac{{{[\tilde{x}-({{x}_{\text{g}}}+{{d}_{x}})]}^{2}}}{4D} \right)\text{d}{{x}_{\text{g}}}\text{d}\tilde{x}}} \right] \\ \left[ \int_{-{{l}_{y}}/2}^{{{l}_{y}}/2}{\int_{-{{l}_{y}}/2}^{{{l}_{y}}/2}{\exp \left( \text{i}k\frac{{{[\tilde{y}-({{y}_{\text{g}}}+{{d}_{y}})]}^{2}}}{4D} \right)\text{d}{{y}_{\text{g}}}\text{d}\tilde{y}}} \right] \\ \end{matrix}.$$](/wp-content/uploads/2016/05/A314073_1_En_10_Chapter_Equ18.gif)
(10.18)
Consider now the first double integral in Eq. (10.18) and make the change of variable from 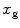 to t, where
to t, where
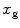 to t, where
to t, where![$$t=\sqrt{\tfrac{k}{2\text{ }\!\!\pi\!\!\text{ }D}}\,[\tilde{x}-({{x}_{g}}+{{d}_{x}})].$$](/wp-content/uploads/2016/05/A314073_1_En_10_Chapter_Equ19.gif)
(10.19)
Then we have
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree