Fig. 1
Spin echo pulse sequence. RF radiofrequency, SS slice selection, PE phase encoding, FE frequency encoding, TE echo time, TR repetition time
The effect of the RF pulse is to increase the energy of the spin system and once the pulse has been switched off the magnetisation returns to thermal equilibrium, i.e. it realigns along the z-direction. Whilst T 2 relaxation does not involve any energy loss, only dephasing of the individual spins, in order to return to thermal equilibrium the spin system needs to give up its energy to the surrounding macromolecular environment, often referred to as the lattice. This energy loss results in an exponential recovery of the magnetisation along the z-direction. This process is known as longitudinal relaxation and is exponential with a time constant of T 1. Again since different tissues interact with the lattice differently, differential T 1 relaxation is an additional MRI contrast mechanism. Since it is only possible to detect signal in the transverse plane, T 1 contrast is achieved by altering the period between subsequent excitation pulses, known as the repetition time (TR). The TR affects how much longitudinal relaxation occurs, so that the subsequent excitation pulse will rotate the differentially recovered magnetisation into the transverse plane. If the TE is kept short then the signal that is detected will largely represent the T 1 relaxation and not any subsequent T 2 transverse relaxation. The difficulty in completely eliminating T 2 relaxation from T 1 images (which would require TE to be zero), or T 1 relaxation from T 2 images (which would require TR to be infinite), results in the images generally being referred to as either T 1– or T 2-weighted. The use of a very short TE with a very long TR can minimise both T 2 and T 1 effects respectively resulting in proton-density weighted images. Figure 2 shows how the transverse (M xy ) decays as a function of TE and the longitudinals (M z ) magnetisation recovers as a function of TR for the three main contrast weightings. Example images from a patient with a large lipid core containing plaque are shown to demonstrate the multiple contrast weightings.
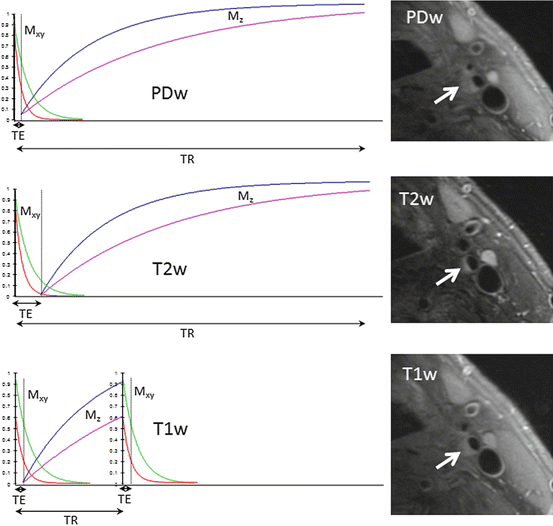

Fig. 2
Proton density (PD), T 2 and T 1 weighted contrast for two different tissue types with example carotid images from a patient with a plaque comprising a large lipid core and fibrous cap (arrows). TE echo time, TR repetition time. M xy transverse magnetisation, M z longitudinal magnetisation
Spatial Localisation
The wavelength of the RF in the body at 1.5 T is typically around 50 cm and is therefore on a scale of the object being imaged, unlike for example X-rays. It is necessary therefore to use a spectroscopic technique in order to achieve an acceptable spatial resolution. In MRI magnetic field gradients are used to spatially encode the NMR signal, followed by an appropriate mathematical process to reconstruct the images. The magnetic field gradients are created by additional coils of wire inside the MRI magnet. These gradient coils create a linear variation in magnetic field with position inside the magnet. These gradient fields are superimposed upon the static magnetic field causing a linear variation in Larmor frequency with position. Spatial localisation of the MRI signal requires the application of three orthogonal gradient fields that are applied, together with the RF pulses at different time points. The combination of RF and gradient pulses are known as a pulse sequence which fulfils the dual requirement of rotating the magnetisation, via the RF pulses, to achieve the desired contrast whilst effectively changing the precessional frequency, via the gradient pulses, to achieve spatial localisation of the signal.
In a standard MRI pulse sequence there are three basic steps in spatial localisation; slice selection, phase encoding and frequency encoding. Slice selection requires that the RF pulses be applied simultaneously with a gradient pulse in one of the three orthogonal directions in order to rotate a thin section of magnetisation by the desired angle. This slice-selection (SS) gradient pulse causes the magnetisation to precess at a positionally dependent frequency in the slice selection direction. The application of an RF pulse at a frequency that matches the precessional frequency at the desired slice location will result in the magnetisation in that location being excited, i.e. rotated. In practice the RF pulse actually excites a small range of precessional frequencies centred about this location so that a desired thickness, e.g. 5 mm, of magnetisation will be excited. The SS gradient is applied for the same duration as the RF pulse in order to rotate the magnetisation by the desired angle, typically 90° in order to create a detectable signal into the transverse plane as described above. Once this “slice” of magnetisation has been rotated into the transverse plane it is necessary to spatially encode the signal within the slice plane using a two-step process. Firstly a phase-encoding (PE) gradient pulse is applied in one of the two in-plane directions. Similar to slice selection this PE gradient pulse causes the magnetisation to precess at a positionally dependent frequency along the PE direction. When the gradient pulse is switched off the spins return to the nominal frequency but retain a relative phase shift with respect to each other. This phase shift constitutes a “pseudo-frequency” along the PE direction. Finally the frequency encoding (FE) gradient is applied along the other in-plane direction. The timing of this gradient pulse is such that it is centred about the time when the echo signal is formed, i.e. TE. The frequency encoding gradient also induces a positionally dependent frequency along the FE direction. The echo signal is digitised in the presence of this gradient and stored in the memory of the reconstruction computer.
The whole pulse sequence is then repeated every TR period. However, with each repetition the amplitude of the PE gradient is changed, so that a different “pseudo-frequency” is induced in the transverse magnetisation prior to the frequency encoding process. Each digitised echo signal, with its own PE gradient-induced phase shift is stored in computer memory. Typically the PE gradient will be applied 256 times in a standard MRI acquisition and each echo will comprise 256 samples. This will result in a two-dimensional (2D) raw data matrix of 256 × 256 samples. Since the spatial information in the images is encoded in the raw data as frequencies the image can be reconstructed by application of an inverse 2D Fourier transformation to the raw data. This method of image acquisition is termed “spin-warp” and was originally developed at the University of Aberdeen by Edelstein and co-workers [7].
Depending upon the choice of TE and TR the reconstructed images will be proton-density, T 2 or T 1 weighted. The spatial resolution in the PE direction will be determined by the number of different PE gradient amplitudes applied and the operator chosen field-of-view that controls the maximum PE gradient amplitude. Since in a basic pulse sequence only one PE gradient is applied per TR the product of the TR and the number of PE steps equals the minimum scan time, e.g. a TR of 3,000 ms multiplied by 256 gradient steps will result in a minimum acquisition time of 12 min and 48 s. The spatial resolution in the FE direction is determined by the number of samples in each echo and the operator chosen field-of-view that controls the FE gradient amplitude.
MRI Hardware
An MRI system comprises four main components. The first is an appropriate magnet to generate the strong static magnetic field (B 0), which is required to induce the nuclear polarisation. The second is a radiofrequency (RF) system that generates the required alternating magnetic field (B 1), at the Larmor frequency and also detects the weak MR signal being returned from the patient. The third component is the gradient system that generates the required linear magnetic field variations that are superimposed upon B 0 and are used to spatially encode the MR signal. The gradient and whole-body RF coils are concentrically positioned inside the bore of the magnet. Figure 3 shows a schematic cross section through a superconducting MRI system. Finally the fourth component consists of a number of computers that are used to provide the user interface, generate the digital representations of the RF and gradient pulses, and also perform the mathematical operations, e.g. Fourier transformation, required to reconstruct an image from the digitised signals returned from the patient.
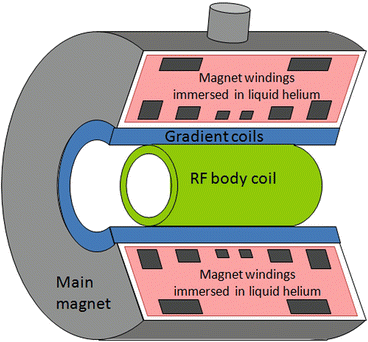

Fig. 3
Cross section through a superconducting MRI system. The figures shows (1) the main magnet windings that generate the static magnetic field, (2) the gradient coils that generate the linear magnetic field variations required for spatial localisation and (3) the radiofrequency (RF) body coil used for transmission of the RF pulses
Magnets
The requirements for the static field are that it should be reasonably strong, stable and uniform. Magnetic field strength or, more accurately, “magnetic flux density”, is measured in the SI derived unit of tesla (symbol T). Whilst it is certainly true that bigger is not necessarily better, there is an approximately linear increase in signal-to-noise ratio (SNR) with increasing field strength. Over the last 30 years of MRI various technologies and designs have been used to create magnets of an appropriate configuration that a human body can be placed inside. These designs have various trade-offs in terms of field strength as well as stability, uniformity and patient acceptance. It was not until the development of superconducting magnet technology that higher field strengths could be achieved. Typical clinical superconducting MRI systems are available at 1.0 T, 1.5 T and 3.0 T, having Larmor frequencies of 42, 64 and 128 MHz, respectively. Most vendors have also developed 7.0 T whole body systems for research purposes, with even higher field strengths, e.g. 11.7 T being custom-developed. Superconducting magnets generate their magnetic field by circulating an electric current through solenoidal coils of niobium-titanium (NbTi) filaments embedded in a copper matrix. At temperatures below approximately 10 K NbTi becomes superconducting, which means it has zero electrical resistance and current will circulate indefinitely without an external power supply. Practically, a superconducting MRI magnet comprises a steel cryostat with the superconducting coils immersed in liquid helium at 4.2 K (−269 °C or −452 °F). Whilst iron-cored or permanent magnet designs can have a C or H-shape and may therefore appear more patient friendly, superconducting MRI system cryostats are most commonly shaped like a cylindrical tube with the patient placed inside the central bore. In addition to the patient, the gradient and the RF body coil are also positioned inside the bore, although hidden from the patient behind fibre-glass covers. Although the diameter of the cryostat bore is approximately 100 cm, once these additional coils are installed the patient accessible bore is reduced to approximately 60 cm. However, in response to demands for improved patient acceptance as well as an increasingly bariatric population, manufacturers have introduced systems to allow 70 cm or greater patient apertures as well as reducing overall magnet lengths.
Whilst a strong, but not necessarily very uniform, B 0 is required to achieve a good nuclear polarisation, an extremely high uniformity is required to perform spatial localisation. The uniformity of B 0 is usually defined as the variation of the field within a spherical volume of a given diameter which, for a 1.5 T magnet would typically be less than 1 part per million (ppm) over a 40 cm diameter spherical volume. Further improvements can be achieved over smaller volumes by a process known as “shimming”, which is often automatically performed by the system for each body part imaged. In addition the field must be temporally very stable, with a typical superconducting magnet having a stability of better than 0.1 ppm/h.
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree