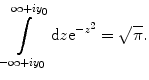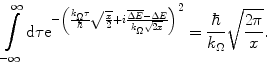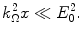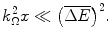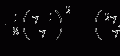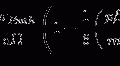(1)
Amersham, Buckinghamshire, UK
18.1.1 Thin Foils
18.1.2 Moderately Thick Foils
18.1.3 Thick Foils
18.1.4 Development of the Chapter
18.3 Vavilov Theory
18.3.1 Introductory Comments
18.3.6 Electrons
18.4.1 Introductory Comments
18.4.3 Edgeworth Series
18.5 Very Thick Foils
Abstract
In this chapter, the pdfs describing charged particle collision energy losses of three different conditions are derived. These results are of 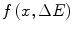 where
where 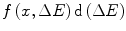 represents the probability that a charged particle has lost kinetic energy between
represents the probability that a charged particle has lost kinetic energy between 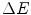 and
and 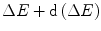 while penetrating into a depth x within a medium.
while penetrating into a depth x within a medium.
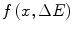 where
where 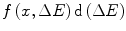 represents the probability that a charged particle has lost kinetic energy between
represents the probability that a charged particle has lost kinetic energy between 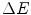 and
and 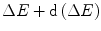 while penetrating into a depth x within a medium.
while penetrating into a depth x within a medium.The differentiator between these pdfs will be the depth of penetration x or, equivalently, the thickness of the medium x. Large thicknesses result in a symmetric Gaussian pdf (under the requirement that the assumptions specified in the previous chapter are met). Reduced thicknesses result in the asymmetric pdfs of the Vavilov and Landau theories. All three conditions are derived in this chapter.
While the asymmetric results noted above provide analytical results that can be solved readily through numerical means, practical calculations, particularly for the rapid requirements of Monte Carlo simulations, are of interest. Such methods are reviewed.
18.1 Introductory Comments
We now derive pdfs for collision energy loss using our variation of the Bothe–Landau equation as our starting tool. However, in so doing, we must not lose sight of the assumptions used to simplify its derivation and which will limit inevitably its applications. Following from the works of Bohr (1915, 1948), Landau (1944) and Vavilov (1957), and the descriptions given by Rossi (1952) and Kase and Nelson (1978), these pdfs are categorised here in terms of the distance within the medium that the charged particles traverse. Equivalently, we can consider the energy losses resulting from the traversal of sections of media (foils) by a beam of charged particles.
18.1.1 Thin Foils
A charged particle traversing a thin section of medium will undergo relatively few interactions with the atoms of that medium. As a result, the energy loss spectrum will closely resemble that of the Rutherford formula of (8.82). Due to the 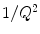 dependence of the collision cross section, the peak of the spectrum will be at lower energy transfers and a tail will extend to higher energy transfers. There will be one critical difference between the pdf and the expression for the spectrum in that the pdf must be normalisable or
dependence of the collision cross section, the peak of the spectrum will be at lower energy transfers and a tail will extend to higher energy transfers. There will be one critical difference between the pdf and the expression for the spectrum in that the pdf must be normalisable or 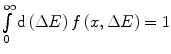 .
.
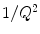 dependence of the collision cross section, the peak of the spectrum will be at lower energy transfers and a tail will extend to higher energy transfers. There will be one critical difference between the pdf and the expression for the spectrum in that the pdf must be normalisable or
dependence of the collision cross section, the peak of the spectrum will be at lower energy transfers and a tail will extend to higher energy transfers. There will be one critical difference between the pdf and the expression for the spectrum in that the pdf must be normalisable or 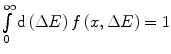 .
.18.1.2 Moderately Thick Foils
Now consider a foil sufficiently thick such that the charged particle traversing it undergoes a larger number of collisions that transfer energy. As such, we can invoke the central-limit theorem and consider the energy loss pdf to approach that of a Gaussian in this case. We will shortly demonstrate that this is obtainable from the Bothe–Landau formula derived in Chap. 17. However, we must temper this consideration by recalling the simplifying assumptions used in the derivation of our version of the Bothe–Landau formula as given in Sect. 17.4.2. In particular, the limit for the foil thickness in this calculation will be defined by (17.19). As you will recall, that assumption is that of the collision energy loss being constant over the thickness of medium being considered. Or, in the same consideration, that the energy dependence of the collision cross section is negligible. With increasing thickness and greater energy loss, that assumption becomes no longer tenable.
18.1.3 Thick Foils
For a thick foil where the assumption of (17.19) is no longer valid, we must consider explicitly the change in the rate of energy loss with decreasing charged particle energy. The simple Gaussian result for the moderately thick foil will have broken down, and different considerations, similar to those used in the development of the Fermi–Eyges theory of multiple Coulomb scatter with energy loss, must be considered.
18.1.4 Development of the Chapter
Having already developed the Bothe–Landau formula, we will use it immediately to calculate the Gaussian pdf of the energy loss for charged particles traversing a moderately thick foil. Here, the central-limit theorem, and our implicit assumption of Poisson statistics in its derivation, yields a Gaussian result provided we remain within the constraints of Sect. 17.4.2.
We will then embark upon the more general solution of Vavilov (1957). His solution of the Chapman–Kolmogorov equation was based upon the application of the Laplace transform rather than our use of the Fourier transform. The result that he achieved is remarkable: it returns the Landau result of energy loss in thin foils and the Gaussian result of energy loss in moderately thick foils.
Following this, we then consider the problem of very thick foils for which there are many collisions, and the change in the rate of energy loss with distance as the particle decelerates can no longer be neglected. In modern medical radiation physics practice, this problem is attacked with Monte Carlo-based solutions. However, to provide a clearer understanding of the problem, we analyse it analytically.
18.2 Derivation of the Gaussian pdf from the Bothe–Landau Equation
In Chap. 17, we derived an integral expression for the energy loss pdf in the form of the Bothe–Landau formula. Adopting the simplification assumptions of Sect. 17.4.2, we proceed to solve the Bothe–Landau equation by first manipulating algebraically the exponent within it:
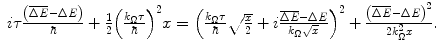
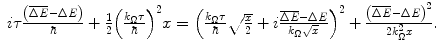
(18.1)
This manipulation allows part of the integrand to be extracted from the integral so as to allow the pdf to be rewritten as
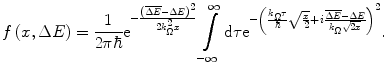
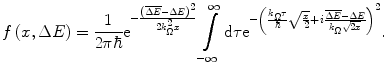
(18.2)
In order to simplify the integral prior to beginning to solve it, we perform a change of variables in (18.2) and create the complex variable
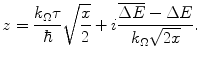
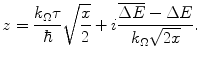
(18.3)
This enables us to rewrite the integral of (18.2) in the much simpler complex form
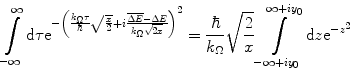
where
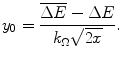
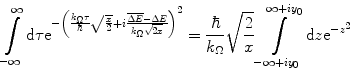
(18.4)
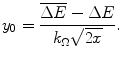
(18.5)
The integral is solved by writing it in another complex form 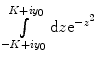 where K is a real constant to be allowed later to go to ∞. As the integrand
where K is a real constant to be allowed later to go to ∞. As the integrand 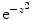 is holomorphic on and within the contour and there are no singularities within the contour, the Cauchy–Goursat theorem states that
is holomorphic on and within the contour and there are no singularities within the contour, the Cauchy–Goursat theorem states that
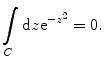
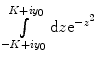 where K is a real constant to be allowed later to go to ∞. As the integrand
where K is a real constant to be allowed later to go to ∞. As the integrand 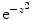 is holomorphic on and within the contour and there are no singularities within the contour, the Cauchy–Goursat theorem states that
is holomorphic on and within the contour and there are no singularities within the contour, the Cauchy–Goursat theorem states that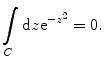
(18.6)
The above result provides the Gaussian probability distribution function for energy loss ΔE at a depth x:
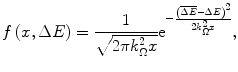
with a mean 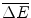 and a variance
and a variance 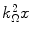 .
.
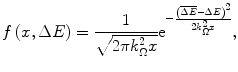
(18.9)
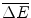 and a variance
and a variance 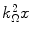 .
.To demonstrate that this result is a pdf, it is necessary to require that the normalisation
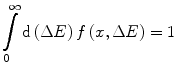
holds true. As the maximum energy loss cannot exceed the incident kinetic energy, (8.10) can be written as
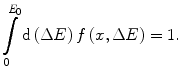
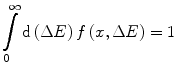
(18.10)
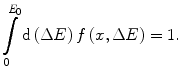
(18.11)
Inserting the expression for the pdf of (18.9) into this integral
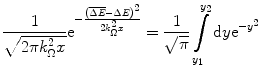
where the change of variables
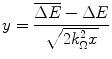
has been used. The limits of integration used in (18.12) are
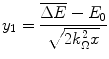
and
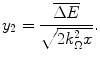
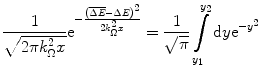
(18.12)
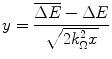
(18.13)
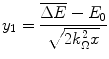
(18.14)
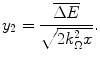
(18.15)
Recall the simplifying assumptions of Sect. 17.4.2 used in the derivation of the Bothe–Landau equation. As these lead to 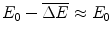 , then the lower limit of integration of (18.14) can be written as
, then the lower limit of integration of (18.14) can be written as
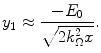
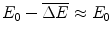 , then the lower limit of integration of (18.14) can be written as
, then the lower limit of integration of (18.14) can be written as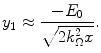
(18.16)
Allowing a small standard deviation, i.e.
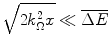
and
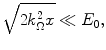
then the limits of integration of (18.12) can be replaced by  . As
. As
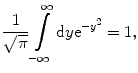
we see that 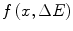 is the pdf sought and is a Gaussian distribution with mean and most probable energy loss
is the pdf sought and is a Gaussian distribution with mean and most probable energy loss
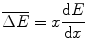
and variance
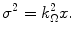
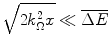
(18.17)
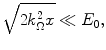
(18.18)
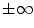 . As
. As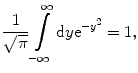
(18.19)
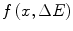 is the pdf sought and is a Gaussian distribution with mean and most probable energy loss
is the pdf sought and is a Gaussian distribution with mean and most probable energy loss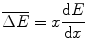
(18.20)
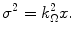
(18.21)
In Chap. 10, we derived expressions for 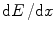 which yield the mean of (18.20). Now, let us calculate an explicit expression of the variance given by (18.21). Recall from our discussion of Sect. 17.4.3 that only hard collisions need be considered in the calculation of the straggling parameter. Hence, in our example, we will evaluate
which yield the mean of (18.20). Now, let us calculate an explicit expression of the variance given by (18.21). Recall from our discussion of Sect. 17.4.3 that only hard collisions need be considered in the calculation of the straggling parameter. Hence, in our example, we will evaluate 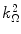 using the Bhabha hard-collision cross section of (9.1) for a massive projectile of mass m, where spin is neglected. Then, from (17.24), (17.25) and (D.15),
using the Bhabha hard-collision cross section of (9.1) for a massive projectile of mass m, where spin is neglected. Then, from (17.24), (17.25) and (D.15),
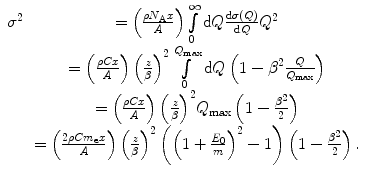
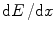 which yield the mean of (18.20). Now, let us calculate an explicit expression of the variance given by (18.21). Recall from our discussion of Sect. 17.4.3 that only hard collisions need be considered in the calculation of the straggling parameter. Hence, in our example, we will evaluate
which yield the mean of (18.20). Now, let us calculate an explicit expression of the variance given by (18.21). Recall from our discussion of Sect. 17.4.3 that only hard collisions need be considered in the calculation of the straggling parameter. Hence, in our example, we will evaluate 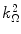 using the Bhabha hard-collision cross section of (9.1) for a massive projectile of mass m, where spin is neglected. Then, from (17.24), (17.25) and (D.15),
using the Bhabha hard-collision cross section of (9.1) for a massive projectile of mass m, where spin is neglected. Then, from (17.24), (17.25) and (D.15),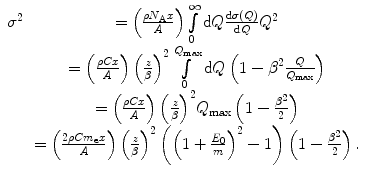
(18.22)
The validity of the result of (18.9) is dependent upon those constraints as noted in Sect. 17.4.2. We thus specify some necessary inequalities. First, from the requirements of the central-limit theorem, the width of this Gaussian pdf (2σ) must be greater than the maximum energy transferred in a single collision, or
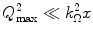
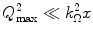
(18.23)
Combining these results, we have the following constraints:
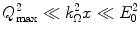
with
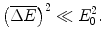
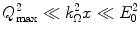
(18.26)
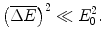
(18.27)
In addition, note that
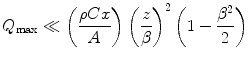
is also a required constraint.
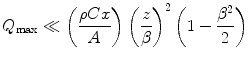
(18.28)
These constraints enable us to define a dimensionless parameter with which to use to test the validity of the Gaussian result:
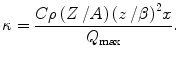
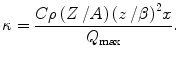
(18.29)
Clearly, from the above inequalities, the Gaussian result is valid for large κ. This parameter will prove useful in our subsequent derivation of the more general Vavilov pdf and permit us to differentiate between those regions of absorber thickness for which the Landau, Vavilov and Gaussian pdfs are valid as to be summarised.
18.3 Vavilov Theory
18.3.1 Introductory Comments
We have demonstrated that a symmetric Gaussian pdf for the energy loss is associated with a large value of κ, which corresponds to both a thick path length x and, through the 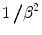 factor, to nonrelativistic particles. For small κ, which corresponds to a thin absorber and/or increasingly relativistic charged particles, the mean energy loss over that absorber will also decrease. However, because the probability of a hard collision remains constant, its relative contribution to the statistical distribution of energy losses will increase as the value of the parameter κ decreases. This leads to a high-energy tail in the energy loss spectrum and an increased asymmetry in the pdf for ΔE. This introduction of asymmetry for small κ will inevitably require us to consider the third-order moment,
factor, to nonrelativistic particles. For small κ, which corresponds to a thin absorber and/or increasingly relativistic charged particles, the mean energy loss over that absorber will also decrease. However, because the probability of a hard collision remains constant, its relative contribution to the statistical distribution of energy losses will increase as the value of the parameter κ decreases. This leads to a high-energy tail in the energy loss spectrum and an increased asymmetry in the pdf for ΔE. This introduction of asymmetry for small κ will inevitably require us to consider the third-order moment, 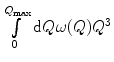 , in addition to our use of
, in addition to our use of 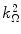 in the description of the energy loss pdf.
in the description of the energy loss pdf.
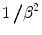 factor, to nonrelativistic particles. For small κ, which corresponds to a thin absorber and/or increasingly relativistic charged particles, the mean energy loss over that absorber will also decrease. However, because the probability of a hard collision remains constant, its relative contribution to the statistical distribution of energy losses will increase as the value of the parameter κ decreases. This leads to a high-energy tail in the energy loss spectrum and an increased asymmetry in the pdf for ΔE. This introduction of asymmetry for small κ will inevitably require us to consider the third-order moment,
factor, to nonrelativistic particles. For small κ, which corresponds to a thin absorber and/or increasingly relativistic charged particles, the mean energy loss over that absorber will also decrease. However, because the probability of a hard collision remains constant, its relative contribution to the statistical distribution of energy losses will increase as the value of the parameter κ decreases. This leads to a high-energy tail in the energy loss spectrum and an increased asymmetry in the pdf for ΔE. This introduction of asymmetry for small κ will inevitably require us to consider the third-order moment, 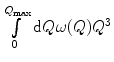 , in addition to our use of
, in addition to our use of 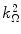 in the description of the energy loss pdf.
in the description of the energy loss pdf.Historically, it was Landau (1944) who first derived a solution to the general Bothe–Landau equation leading to an asymmetric energy loss pdf. He achieved this through the use of Laplace transforms. Landau’s result, however, was derived for the Rutherford differential cross section (which is equivalent to neglecting the 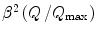 term in the Bhabha cross section of (9.1)) and was dependent upon a variety of approximations.
term in the Bhabha cross section of (9.1)) and was dependent upon a variety of approximations.
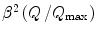 term in the Bhabha cross section of (9.1)) and was dependent upon a variety of approximations.
term in the Bhabha cross section of (9.1)) and was dependent upon a variety of approximations.18.3.2 Derivation of the Vavilov pdf
This derivation follows Vavilov’s approach and solves the integro-differential continuity equation for f(x, ΔE) by using the Laplace transform with the following transform pairs (Appendix B.2):
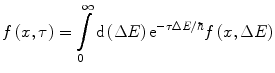
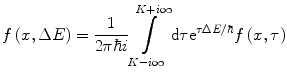
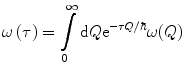
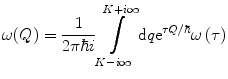
where K




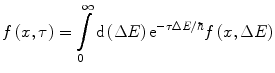
(18.30)
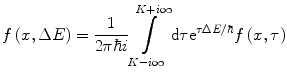
(18.31)
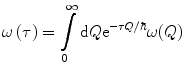
(18.32)
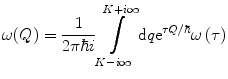
(18.33)
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree