(1)
Faculty of Medicine, Department, of Oncology and Medical Physics Unit, McGill University, Montreal, Québec, Canada
Abstract
Chapter 4 consists of 13 problems that in 4 sections cover production of the two types of x rays: characteristic radiation and bremsstrahlung radiation in addition to two types of radiation remotely related to x rays: synchrotron radiation (also called magnetic bremsstrahlung) and Čerenkov radiation. Characteristic x rays and low energy bremsstrahlung produced in x-ray tubes are used extensively in diagnostic imaging while high energy x rays produced in linear accelerators provide the basis of modern radiotherapy.
Characteristic x rays are produced by electronic transitions in atoms triggered by vacancies in inner electronic shells of the absorber atom. Inner shell atomic vacancies are produced through one of 8 possible processes and migrate toward the outer atomic shell (valence shell) of the absorber atom through one or more steps. The energy released in an electronic transition from one electronic orbit to another is either emitted in the form of a characteristic photon or transferred to an orbital electron of the absorber atom by triggering release of this electron as an Auger electron. Bremsstrahlung x rays, on the other hand, are produced by an inelastic Coulomb interaction between light charged particle and the nucleus of the absorber atom. The spectrum of characteristic x-ray photons is discrete and characteristic of the absorber material; the spectrum of bremsstrahlung is continuous and contains photons with energy from 0 to the kinetic energy of the light charged particle that produced the photon.
The first few problems in this chapter (Sect. 4.1) address issues related to characteristic radiation, such as the Siegbahn and IUPAC notation for designation of electronic levels in an atom as well as rules governing production of characteristic x-ray line spectra. Problems in Sect. 4.2 deal with theoretical aspects of the production of bremsstrahlung radiation and the chapter concludes with several questions covering practical and theoretical aspects of and synchrotron radiation (Sect. 4.3) and Čerenkov radiation (Sect. 4.4).
Chapter 4 consists of 13 problems that in 4 sections cover production of the two types of x rays: characteristic radiation and bremsstrahlung radiation in addition to two types of radiation remotely related to x rays: synchrotron radiation (also called magnetic bremsstrahlung) and Čerenkov radiation. Characteristic x rays and low energy bremsstrahlung produced in x-ray tubes are used extensively in diagnostic imaging while high energy x rays produced in linear accelerators provide the basis of modern radiotherapy.
Characteristic x rays are produced by electronic transitions in atoms triggered by vacancies in inner electronic shells of the absorber atom. Inner shell atomic vacancies are produced through one of 8 possible processes and migrate toward the outer atomic shell (valence shell) of the absorber atom through one or more steps. The energy released in an electronic transition from one electronic orbit to another is either emitted in the form of a characteristic photon or transferred to an orbital electron of the absorber atom by triggering release of this electron as an Auger electron. Bremsstrahlung x rays, on the other hand, are produced by an inelastic Coulomb interaction between light charged particle and the nucleus of the absorber atom. The spectrum of characteristic x-ray photons is discrete and characteristic of the absorber material; the spectrum of bremsstrahlung is continuous and contains photons with energy from 0 to the kinetic energy of the light charged particle that produced the photon.
The first few problems in this chapter (Sect. 4.1) address issues related to characteristic radiation, such as the Siegbahn and IUPAC notation for designation of electronic levels in an atom as well as rules governing production of characteristic x-ray line spectra. Problems in Sect. 4.2 deal with theoretical aspects of the production of bremsstrahlung radiation and the chapter concludes with several questions covering practical and theoretical aspects of and synchrotron radiation (Sect. 4.3) and Čerenkov radiation (Sect. 4.4).
4.1 X-Ray Line Spectra
4.1.Q1 (104)
An atom with an electronic vacancy in its inner shell is in a highly excited state and returns to its ground state through one or several electronic transitions. In each of these transitions an electron from a higher atomic shell fills the shell vacancy and the energy difference in binding energy between the initial and final shell or sub-shell is emitted from the atom in one of two ways: either (1) in the form of characteristic (fluorescence) radiation or (2) radiation-less in the form of Auger electrons, Coster–Kronig electrons, or super Coster–Kronig electrons.
(a)
Define an atomic shell vacancy, list the two types of shell vacancy, and briefly describe the ultimate fate of a shell vacancy.
(b)
List at least 8 processes resulting in production of a primary atomic shell vacancy and briefly describe each process.
(c)
Define the fluorescence yield ω and sketch a plot of ω against atomic number Z of the absorber for the K, L, and M electronic shells.
SOLUTION:
(a) A shell vacancy is defined as an electron missing from the normal complement of electrons in a given atomic shell. Two types of vacancy are known: (1) primary and (2) secondary.
(1) Primary shell vacancy occurs when an atomic electron is displaced from the atomic cloud through one of 8 known processes that fall into 5 categories: incident photon–atom interactions; nuclear effects; incident charged particle–atom Coulomb interactions, Auger effect, and positron annihilation. Primary vacancy can occur in any one of the electronic shells of an atom, making a positive ion (anion) out of the neutral atom.
(2) Secondary shell vacancy occurs when an electron makes a transition from a higher-level electronic shell to a lower-level electronic shell in an atom, meaning that the vacancy moves in the opposite direction. The transition energy is emitted in the form of characteristic (fluorescence) radiation or is transferred to an electron in a higher-level shell that is ejected as Auger electron leaving behind a primary vacancy.
Note: When a primary vacancy is created, the shell electron leaves the electronic cloud and the atom loses an electron through creation of a vacancy and thus undergoes the process of ionization. When a secondary vacancy occurs, an existing vacancy merely moves from a lower-level shell to a higher-level shell of the same atom and no new vacancy is produced in the atom; however, the transition energy is emitted as a characteristic photon or is transferred to an Auger electron. All primary vacancies produced in an atom migrate to the outer shell of the positive ion either directly or through creation of intermediate secondary vacancies. Free electrons from the ion’s environment will fill the ion’s outer shell vacancies and the ion will revert to its original neutral state.
(b) Eight processes that result in production of a primary shell vacancy are as follows:
(1) Photoelectric effect. A photon-atom interaction whereby the photon is completely absorbed by the atom and its energy is given to an orbital shell electron. The orbital electron is ejected from the atom as a photoelectron leaving behind a shell vacancy.
(2) Compton scattering. A photon-orbital electron interaction whereby the photon is scattered with a lower energy by a loosely bound orbital electron and energy difference between the incident and scattered photon is absorbed by an orbital electron. The orbital electron is consequently ejected from the atom as a Compton (recoil) electron leaving behind a shell vacancy.
(3) Triplet production. A photon-orbital electron interaction whereby the photon interacts with the Coulomb field of an orbital electron of the absorber atom. The photon disappears and an electron-positron pair is created (materialization). To conserve momentum, the orbital electron absorbs part of the incident photon energy and is consequently ejected from the atom leaving behind a shell vacancy.
(4) Charged particle Coulomb interaction with atom. A charged particle as it traverses absorbing medium interacts through Coulomb force with orbital electrons and nuclei of atoms in the absorber. The orbital electrons absorb part of the charged particle energy and are either ejected from the atom or excited to higher energy levels leaving behind shell vacancies in the absorber atoms.
(5) Internal conversion. A nuclear decay process whereby the energy of an excited nucleus is given to an orbital electron. As a result the orbital electron is ejected from the absorber atom leaving behind a shell vacancy.
(6) Electron capture. A nuclear decay process whereby an excited nucleus captures an orbital electron from one of the inner shells of the atom. The captured electron leaves behind a shell vacancy and in the nucleus a proton is converted into a neutron.
(7) Positron annihilation. A positron traversing absorbing medium annihilates with an orbital electron in a process that creates several (most often two) annihilation quanta and an electronic vacancy in the absorber atom. Most frequently, the annihilation occurs after the positron lost all of its kinetic energy through Coulomb interactions with absorber atoms; however, more rarely annihilation can also occur when the positron still carries kinetic energy and the annihilation process is then called annihilation-in-flight.
(8) Auger effect. A process by which an atom with a vacancy in one of its orbital shells, except for the outer shell, relaxes. As an orbital electron makes a transition from a higher-level shell to fill the vacancy, the transition energy is emitted either in the form of characteristic (fluorescence) photon or is transferred to a higher-level shell electron that is emitted as an Auger electron leaving behind a primary shell vacancy.
The first three processes: photoelectric effect, Coulomb scattering, and triplet production (electronic pair production) fall into the category of photon interaction with absorber atom. The fourth process includes charged particle Coulomb interaction with orbital electrons of absorber atoms, while Internal conversion and electron capture fall into the category of nuclear effects.
(c) Fluorescence yield of a given shell (K, L, or M) is defined as the number of fluorescence (characteristic) photons emitted per vacancy in the shell. It can also be regarded as the probability, after creation of an electronic shell vacancy, of fluorescence photon emission as opposed to Auger electron emission.
Fluorescence yields ω K, ω L, and ω M for K, L, and M electronic shell vacancies, respectively, are plotted in Fig. 4.1 against atomic number Z for all elements with 1≤Z≤100. The anchor points for ω versus Z plot are clearly indicated in Fig. 4.1. The anchor points are:
![$$\begin{array}{@{}l@{\qquad}l@{\qquad}l} \mbox{For}\ \omega_{\mathrm{K}}{:}\quad [Z \le 10,\omega _{\mathrm{K}} = 0]; & [Z = 30,\omega _{\mathrm{K}} = 0.50]; & [Z \ge 90,\omega _{\mathrm{K}} \approx 0.96]\\ \mbox{For}\ \omega _{\mathrm{L}}{:}\quad [Z \le 30,\omega _{\mathrm{L}} = 0]; & [Z = 70,\omega _{\mathrm{L}}= 0.25]; & [Z = 100,\omega _{\mathrm{L}} \approx 0.5]\\ \mbox{For}\ \omega _{\mathrm{M}}{:}\quad [Z < 70,\omega _{\mathrm{M}} = 0]; & [Z = 100,\omega _{\mathrm{M}} \approx 0.05] & \end{array} $$](/wp-content/uploads/2016/04/A212719_1_En_4_Chapter_Equa.gif) The following features of fluorescence yield ω are noteworthy:
The following features of fluorescence yield ω are noteworthy:
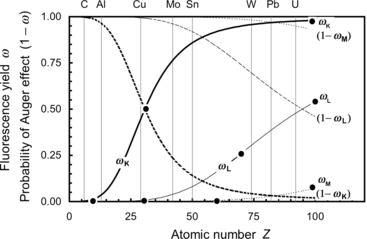
![$$\begin{array}{@{}l@{\qquad}l@{\qquad}l} \mbox{For}\ \omega_{\mathrm{K}}{:}\quad [Z \le 10,\omega _{\mathrm{K}} = 0]; & [Z = 30,\omega _{\mathrm{K}} = 0.50]; & [Z \ge 90,\omega _{\mathrm{K}} \approx 0.96]\\ \mbox{For}\ \omega _{\mathrm{L}}{:}\quad [Z \le 30,\omega _{\mathrm{L}} = 0]; & [Z = 70,\omega _{\mathrm{L}}= 0.25]; & [Z = 100,\omega _{\mathrm{L}} \approx 0.5]\\ \mbox{For}\ \omega _{\mathrm{M}}{:}\quad [Z < 70,\omega _{\mathrm{M}} = 0]; & [Z = 100,\omega _{\mathrm{M}} \approx 0.05] & \end{array} $$](/wp-content/uploads/2016/04/A212719_1_En_4_Chapter_Equa.gif)

Fig. 4.1
Fluorescence yields ω K, ω L, and ω M against atomic number Z. Also shown are probabilities for Auger effect 1−ω K, 1−ω L, and 1−ω M. Data are from Hubbell
(1) A plot of the fluorescence yield ω K against absorber atomic number Z results in a sigmoid shaped curve with ω K ranging from ω K=0 for low atomic number (Z<10) elements through ω K=0.5 at Z=30 to ω K=0.96 at very high Z.
(2) For the L-shell vacancy the fluorescence yield ω L is zero at Z<30 and then rises with Z to reach a value ω L=0.5 at Z=100.
(3) Fluorescence yield ω M is zero for all elements with Z<60, and for Z>60 it rises slowly with increasing Z to attain a value ω M≈0.05 for very high Z absorbers, indicating that fluorescence emission from the M shell and higher level electronic shells is essentially negligible for all absorbers, even those with very high atomic number Z.
(4) For a given electronic shell a plot of 1−ω against atomic number Z shows the probability for Auger effect following creation of a vacancy in an electronic shell with the exception of the outer shell of the absorber atom.
(5) For a given absorber, the higher is the shell level (i.e., the lower is the shell binding energy), the lower is the fluorescence yield ω and, consequently, the higher is the probability for Auger effect (1−ω).
4.1.Q2 (105)
Atomic energy level diagram for tungsten (Z=74) in ground state is shown in Fig. 4.1. Energy levels are identified using the spectroscopic notation (e.g., 1s1/2, 2s1/2,… etc.) as well as the IUPAC x-ray notation (e.g., K, L1, L2,… etc.).
(a)
For each energy level of tungsten provide in Fig. 4.2 the quantum numbers n, l, j, and m j of electrons occupying the energy level.
(b)
For each energy level of tungsten provide in Fig. 4.2 the number of electrons residing in the level.
(c)
Complete Table 4.1 that deals with information pertinent to the shell and subshell structure of tungsten.
(d)
(e)
Transition L1–O3 (referring to transition of vacancy rather than the actual transition of an electron) is indicated on the energy level diagram of Fig. 4.2. Is this an allowed or forbidden transition?
(f)
Assume that there is an electronic vacancy in the L2 subshell. Following the standard selection rules for dipolar transitions and using the IUPAC notation, show on Fig. 4.2 and list separately all allowed electronic transitions to the L2 subshell.
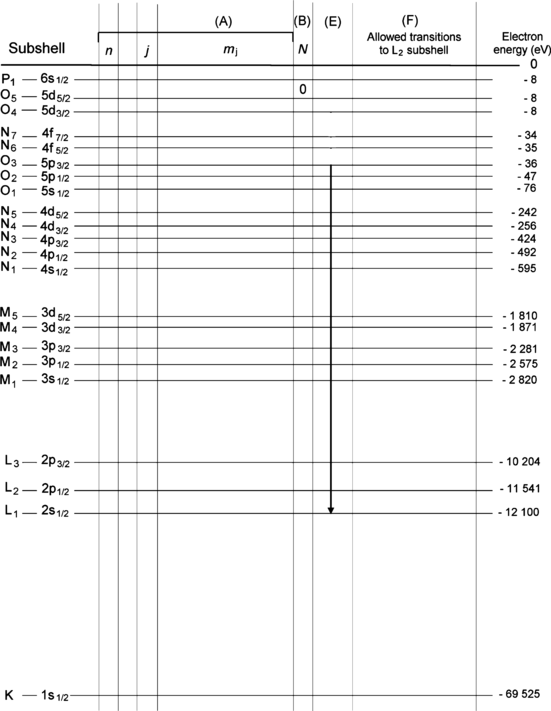
Fig. 4.2
Atomic energy level diagram of tungsten (Z=74) including energy levels of the K shell and all subshells. First column shows the designation of subshells in the IUPAC notation and the last column shows the energy levels of the subshells in electron volts (eV)
SOLUTION:

(d)
Electronic configuration of tungsten in atomic ground state is given as:
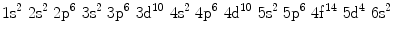
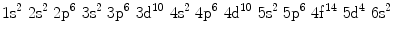
(e)
The transition L1–O3 involves the vacancy transition from subshell L1 to subshell O3, corresponding to the actual electron transition in the opposite direction from O3 to L1. The question on whether this is an allowed or forbidden transition will be answered by checking the applicable selection rules Δℓ=±1 and Δj=0, ±1. Since in this transition Δℓ=+1 and Δj=+1, we conclude that this is an allowed transition.
Table 4.1
Main characteristics of the shell and subshell structure of tungsten
Principal quantum number n | Electronic shell | Shell population | Electronic subshell | Orbital quantum number | Subshell population |
|---|---|---|---|---|---|
K | 1s | ||||
L | 2s | ||||
– | 2p | ||||
M | 3s | ||||
– | 3p | ||||
– | 3d | ||||
N | 4s | ||||
– | 4p | ||||
– | 4d | ||||
– | 4f | ||||
O | 5s | ||||
– | 5p | ||||
– | 5d | ||||
P | 6s |

Fig. 4.3
Atomic energy level diagram of tungsten including shell and subshell structure following the IUPAC convention (first column); quantum numbers for individual subshells in column (A); number of electrons N in each subshell in column (B); transition L1–O3 (vacancy) in column (E); all allowed transitions (vacancy) from L2 subshell in column (F); and energy level in electron volts for each subshell (right hand column)
Table 4.2
Main characteristics of shell and subshell structure of tungsten
Principal quantum number n | Electronic shell | Shell population | Electronic subshell | Orbital quantum number | Subshell population |
|---|---|---|---|---|---|
1 | K | 2 | 1s | 1 | 2 |
2 | L | 8 | 2s | 1 | 2 |
2p | 2 | 6 | |||
3 | M | 18 | 3s | 1 | 2 |
3p | 2 | 6 | |||
3d | 3 | 10 | |||
4 | N | 32 | 4s | 1 | 2 |
4p | 2 | 6 | |||
4d | 3 | 10 | |||
4f | 4 | 14 | |||
5 | O | 12 | 5s | 1 | 2 |
5p | 2 | 6 | |||
5d | 3 | 4 | |||
6 | P | 2 | 6s | 1 | 2 |
Table 4.3
Allowed transitions to fill a vacancy in the L2 subshell of tungsten atom
N | Transition | Δℓ | Δj |
|---|---|---|---|
1 | L2–M1 | −1 | 0 |
2 | L2–M4 | +1 | 1 |
3 | L2–N1 | −1 | 0 |
4 | L2–N4 | +1 | 1 |
5 | L2–O1 | −1 | 0 |
6 | L2–O4 | +1 | 1 |
7 | L2–O1 | −1 | 0 |
4.1.Q3 (106)
Atomic energy level diagram for tungsten is shown in Fig. 4.4. Assume that an electron from the M2 subshell fills an electronic vacancy that was created in the K shell. As shown schematically on the graph, there are two possible options (A and B) available to the excited atom for release of energy made available during the M2–K electronic transition.
(a)
List and briefly define at least six processes by which the K shell vacancy in the tungsten atom might have been produced.
(b)
Briefly describe options A and B for the release of the transition energy E(M2–K).
(c)
Discuss the branching ratio between options A and B.
(d)
Explain the fate of the M2 vacancy that was produced in the initial M2–K electronic transition.
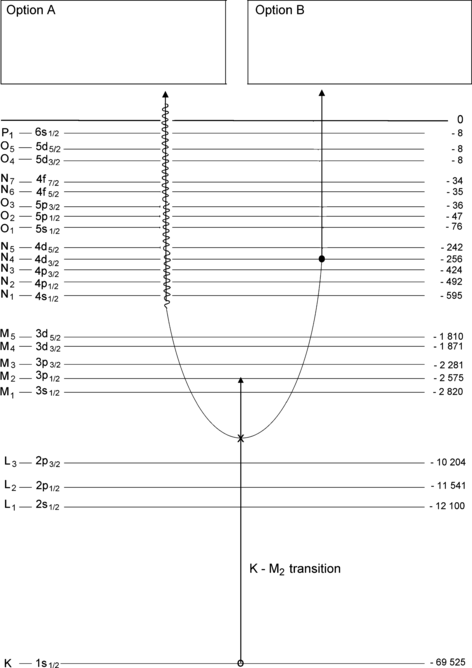
Fig. 4.4
Atomic energy level diagram of tungsten with a vacancy in the K shell that is filled by an electron from the M2 subshell (transition K–M2 describes the transition of the vacancy)
SOLUTION:
(a) The electronic vacancy in the K shell of tungsten could have been produced through an assortment of different effects that can be placed into three major categories of interactions (see Prob. 104) with the K shell orbital electron: Coulomb inelastic collision of light charged particle (electron or positron) or heavy charged particle (proton, deuteron, alpha, etc.); photon interactions (photoelectric effect, Compton effect, and electronic pair production) and nuclear effects (internal conversion or K capture).
(b) As shown schematically in Fig. 4.5, there are two options (A and B) available for dissipation of the K–M2 transition energy ΔE=E(M2)−E(K)=66.95 keV.
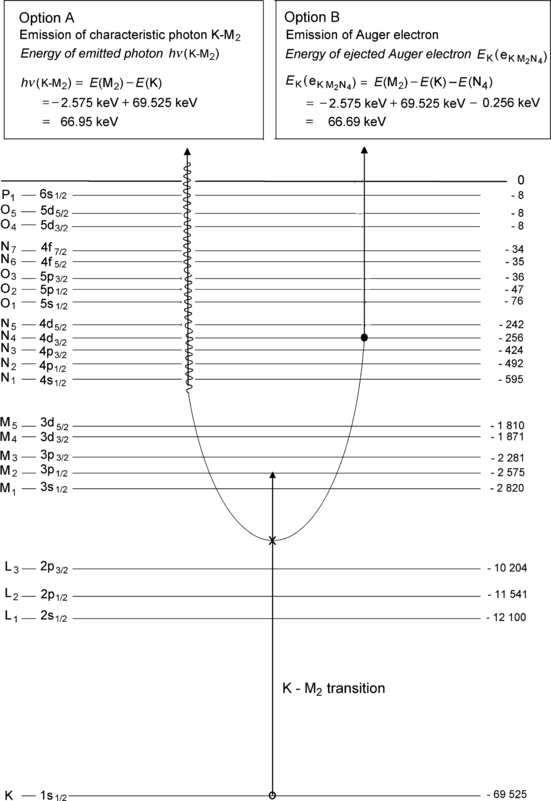

Fig. 4.5
Atomic energy level diagram of tungsten with an electronic vacancy in the K shell that is filled by an electron from the M2 subshell. The two options: A as emission of characteristic (also called fluorescence) photon and B as emission of an Auger electron are described
(1) In option A the transition energy is emitted in the form of a characteristic (fluorescence) photon that (i) is referred to as a K–M2 photon because it originated from a vacancy transition from the K shell to the M2 subshell and (ii) is referred to as characteristic photon because its energy of 66.95 keV is characteristic of the tungsten atom.
(2) In option B the transition energy ΔE=E(M2)−E(K)=66.95 keV is transferred to an orbital electron from L shell or higher and the electron, referred to as an Auger electron, is ejected from the tungsten atom. In our example given in Fig. 4.5 the transition energy is transferred to a N4 subshell orbital electron that is ejected from the nucleus as an 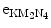 Auger electron with kinetic energy E K=ΔE−E B(N4)=E(M2)−E(K)−E B(N4)=66.69 keV through a process called the Auger effect.
Auger electron with kinetic energy E K=ΔE−E B(N4)=E(M2)−E(K)−E B(N4)=66.69 keV through a process called the Auger effect.
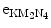 Auger electron with kinetic energy E K=ΔE−E B(N4)=E(M2)−E(K)−E B(N4)=66.69 keV through a process called the Auger effect.
Auger electron with kinetic energy E K=ΔE−E B(N4)=E(M2)−E(K)−E B(N4)=66.69 keV through a process called the Auger effect.(c) The branching between the two options (emission of a characteristic photon or ejection of an Auger electron) is governed by the fluorescence yield ω for the given atom and for the given atomic shell of the atom. The fluorescence yield for a given shell is defined as the number of fluorescence photons emitted per vacancy in the given shell. Alternatively, fluorescence yield can also be regarded as the probability, after the creation of a shell vacancy, of fluorescence emission as opposed to emission of Auger electron.
The fluorescence yield ω is plotted with solid curves for K, L, and M shell electron vacancies in Fig. 4.6 against atomic number for all elements. Also plotted (with dashed lines) is the probability for Auger effect (1−ω) against atomic number for all elements. As shown in Fig. 4.6, the fluorescence yield for the K shell vacancy in tungsten is ω K=0.95, while the probability for Auger effect following a K shell vacancy in tungsten is 1−ω K=0.05.
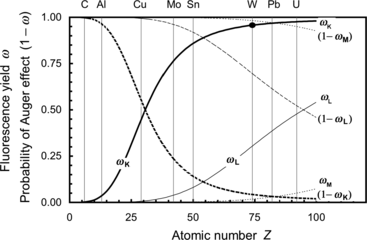

Fig. 4.6
Fluorescence yield (solid curves) and probability of Auger effect against atomic number for elements between Z=1 to Z=100
4.1.Q4 (107)
Figure 4.7 shows the atomic energy level diagram of tungsten atom consisting of the K shell and all subshells in addition to showing the electron population of each subshell.
(a)
Assume that there is a vacancy in the K shell and show three different possible paths of migration of the vacancy to the outer subshell P1. Each of the three paths should consist of at least 5 allowed transitions (steps). Identify each step in the IUPAC notation.
(b)
Assume that there is a vacancy in the N2 subshell. The vacancy will be filled by an electron from a higher-level subshell and the transition will be accompanied either by emission of a characteristic photon or an Auger electron, Coster-Kronig electron or super Coster-Kronig electron. Show three possible electronic transitions to the N2 subshell: one that could result in a standard Auger electron, one that could engender a Coster-Kronig electron, and one that could result in a super Coster-Kronig electron. For each of these electrons provide appropriate label in IUPAC notation and their kinetic energy.

Fig. 4.7
Energy level diagram for tungsten atom (Z=74). Electron vacancies in the K shell and the N2 subshell are shown with hollow circles, the electrons in the K shell and all subshells are shown with solid circle
SOLUTION:
Figure 4.8 deals with migration of two electronic vacancies (one in the K shell and the other in the N2 subshell) toward the outer subshell (P1) in a tungsten atom.


Fig. 4.8
Energy level diagram of tungsten atom. (A) shows three of many possible pathways that a vacancy in the K shell of tungsten can take in its migration to the outer subshell P1. Each pathway contains 6 steps and each step is identified in the IUPAC notation. (B) deals with a vacancy in the N2 subshell and shows three possible transitions, one resulting in ejection of an Auger electron through standard Auger effect, one resulting in ejection of a Coster-Kronig electron through Coster-Kronig effect, and one resulting in super Coster-Kronig electron through super Coster-Kronig effect
Figure 4.8(A) shows three examples of possible paths for the K shell vacancy migration toward the P1 subshell (also referred to as the outer shell or valence shell of tungsten atom), each path progressing through 6 electronic transitions (steps). Each step is identified in the IUPAC notation and fulfills the dipolar selection rules on the angular momentum quantum number (Δℓ=±1) as well as on the total angular momentum quantum number (Δj=0, ±1). The K–L2 and K–L3 transitions were labeled 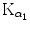 and
and 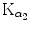 , respectively, in the classical Siegbahn notation.
, respectively, in the classical Siegbahn notation.
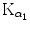 and
and 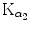 , respectively, in the classical Siegbahn notation.
, respectively, in the classical Siegbahn notation.Figure 4.8(B) shows the start of three possible pathways of the vacancy migration from the N2 subshell toward the P1 subshell. Each of these steps is followed by energy transfer to an orbital electron through three different types of Auger effect: standard Auger effect, Coster-Kronig effect, and super Coster-Kronig effect. The distinction among the three different effects is as follows:
(i)
In the standard Auger effect the primary transition occurs between two shells and the transition energy is transferred to an orbital electron from the initial shell or an even higher-level shell. The ejected electron is called an Auger electron.
(ii)
In Coster-Kronig effect the transition energy originates from two subshells of a given shell and is transferred to an electron in another (higher-level) shell. The emitted electron is called a Coster-Kronig electron.
(iii)
In super Coster-Kronig effect the transition energy that, like in (ii), originates from two subshells of a given shell is transferred to a subshell electron within the shell in which the primary transition occurred. The emitted electron is called super Coster-Kronig electron.
4.1.Q5 (108)
Figure 4.9 displays an atomic energy level diagram of tungsten. An incident photon of energy hν=150 keV interacts with a K shell electron. In the interaction the photon disappears, the K-shell electron is ejected as a photoelectron and the vacancy, created in the K shell, migrates through many steps toward the P1 subshell. Each step in the vacancy migration to the P1 subshell and the subsequent return of the atom to ground state and to neutral state by attracting an electron from environment into the P1 state is identified on the diagram with a box containing three labels: (A) Identification of the particle (photon or electron) produced or released or of energy transfer process; (B) Identification of the transition in the IUPAC notation; and (C) Specification of particle energy or transition energy in electron volts (eV).
(a)
Provide answers for each step in the vacancy migration.
(b)
Provide a summary for energy released in the form of photons and electrons.
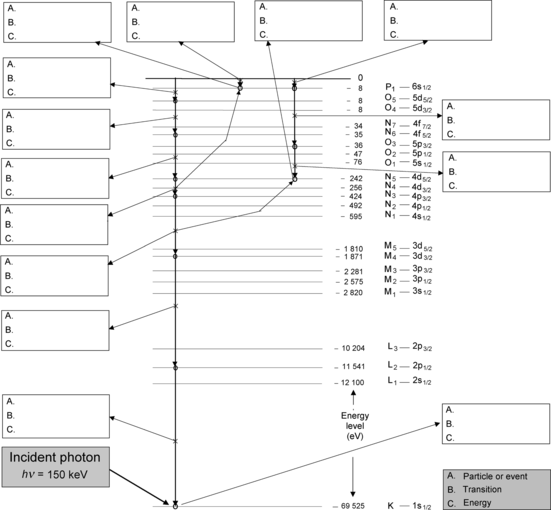
Fig. 4.9
Atomic energy level diagram of tungsten and an example of K-shell vacancy migration toward the outer shell and eventual neutralization of the atom
SOLUTION:
(a) Each step in the vacancy migration to the outer shell of tungsten involves either production of a characteristic (fluorescence) photon or an Auger electron. Figure 4.10 provides answers (A), (B), and (C) for each individual step.
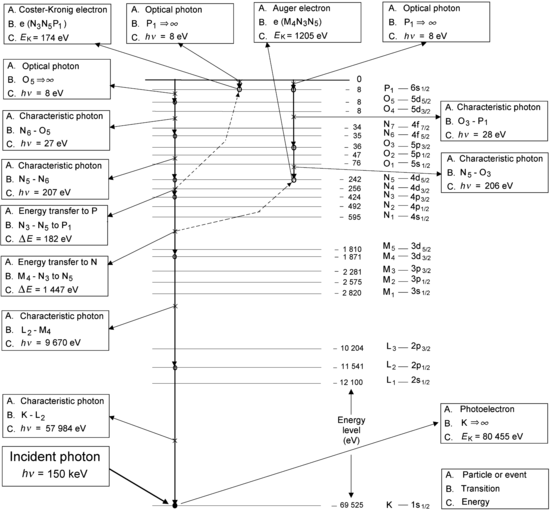

Fig. 4.10
Example of K-shell vacancy migration toward the outer shell of tungsten atom. The 6 transitions producing characteristic radiation and two transitions producing Auger electrons are clearly identified and their IUPAC notation as well as energy are also given. The tungsten atom was assumed to have been neutral before the incident photon interaction and the 3 optical photon transitions in the diagram represent the process of the tungsten ion acquiring 3 free electrons to become neutral again
(b) Summary for the example of vacancy migration from K shell to P1 subshell is given in Table 4.4. The migration in this example consists of 4 transitions producing a characteristic photon and 2 transitions producing an Auger electron. The 8 eV optical transitions result from neutralization of tungsten ion through attracting stationary electrons from the environment.
Table 4.4
Summary of an example of K-shell vacancy migration to P1 subshell in tungsten
Transition | Energy (eV) | ||
|---|---|---|---|
1 | K–L2 | Characteristic photon | 57 984 |
2 | L2–M4 | Characteristic photon | 9 670 |
3 | M4–N3 | Energy transfer to N5 | 1 447 |
4 | N3–N5 | Energy transfer to P1 | 182 |
5 | N5–N6 | Characteristic photon | 207 |
6 | N6–O5 | Characteristic photon | 27 |