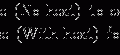Quantification and Measurement of Dose

, Foster D. Lasley², Indra J. Das², Marc S. Mendonca² and Joseph R. Dynlacht²

(1)

Department of Radiation Oncology, CHRISTUS St. Patrick Regional Cancer Center, Lake Charles, LA, USA

(2)

Department of Radiation Oncology, Indiana University School of Medicine, Indianapolis, IN, USA

Definitions

Gy: Gray: SI derived unit of absorbed dose in Joules per kilogram.
- 1 Gy = 100 rads
- 10⁻⁶ = micro- (μGy)
- 10⁻³ = milli- (mGy)
- 10⁻² = centi- (cGy) = 1 rad
Sv: Sievert: SI derived unit of equivalent radiation dose and effective radiation dose (also in Joules per kilogram)
- Different from Gy and used for safety and regulations. Involves weighting factors for absorbed dose.
- 1 Sv = 100 rem (older unit of equivalent/effective dose).
- 10⁻⁶ = micro- (μSv)
- 10⁻³ = milli- (mSv)
R: Roentgen: older unit of measurement for air KERMA or exposure
- 10⁻³ = mill- (mR)
- 1 R = 2.58 × 10⁻⁴ Coulombs per Kilogram
  
  C/kg is the SI unit for air KERMA or exposure – there is no eponym presently.
dmax: the depth where the maximum dose is deposited (usually given in centimeters).
Dmax: the maximum dose as a percentage of the prescription dose (describes the magnitude of a hot spot).

KERMA and Dose

KERMA – Kinetic Energy Released in Media (the A was added to prevent it from being a dirty word in German apparently). Technically, it is defined as:

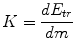
$K=\frac{d{ E}_{tr}}{ d m}$

(6.1)
E _tris the sum of the initial transferred kinetic energies of all charged particles set in motion by photons in mass (m).
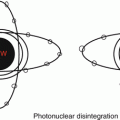
In other words, KERMA is the energy transferred to the secondary electrons from the primary photons. It is NOT the same as absorbed dose but it has the same basic units of measurement (J/kg) (Fig. 6.1).

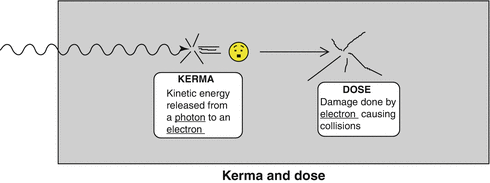
Fig. 6.1

KERMA vs Dose: KERMA is the kinetic energy transferred from the photon to the electron. Dose is the energy deposited to the medium in the form of ionizations and excitations.

Equation Terms

Linear attenuation coefficient (μ):
- The fraction of how many photons are removed per path-length either from scattering out or from transferring their energy to electrons.
- Measured in cm ⁻¹.
- Dependence:
  
  Electron density: heavier atoms like calcium in bone get more photoelectric effect and pair production.
  
  Physical density (ρ): Muscle attenuates more than lung even though both tissues are mostly water by mass.
- By dividing μ over ρ, you get the “average mass energy transfer coefficient” with units of Kg⁻¹ denoted below:
  
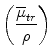
  $\left(\frac{{\overline{\mu}}_{tr}}{\rho}\right)$
Energy fluence (Eϕ) or flux (Ψ) is the total energy per unit area (a) of a beam, as follows:

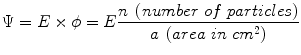
$\Psi = E\times \phi = E\frac{n\;\left( number\; of\; particles\right)}{a\;\left( area\ in\ c{m}^2\right)}$

(6.2)

Kerma Equations

Since we now have energy fluence over a beam cross section (Ψ) and energy lost per unity mass in a linear fashion, we can combine the mass energy transfer coefficient, Eqs. 6.1 and 6.2 into the following equation:

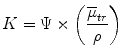
$K=\Psi \times \left(\frac{{\overline{\mu}}_{tr}}{\rho}\right)$

(6.3)
Even though the energy initially comes from photons, it is the electrons set in motion by the photons that do the final damage (or dose). Most of the energy from the electrons (at least for our purposes) can be considered collisional Kerma (K _c).
Some of the electrons will bend their path, especially if there is metal or other high Z material nearby and create bremsstrahlung photons which then escape the medium and contribute nothing to the absorbed dose. This is called radiative Kerma (K _r).

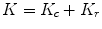
$K={K}_c+{K}_r$

(6.4)
Only K_c contributes to absorbed dose and we do not really care about K_r because it is a small number translates to a correctional factor. Since we are only interested in K_c, we can rearrange Eq. 6.3 to describe what we are looking at when we turn a beam on:

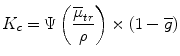
${K}_c=\Psi \left(\frac{{\overline{\mu}}_{tr}}{\rho}\right)\times \left(1-\overline{g}\right)$

(6.5)
Where g is the fraction of energy lost to electrons causing bremmstrahlung photons (it is a substitution for what would have been the K_r term) (Fig. 6.2).

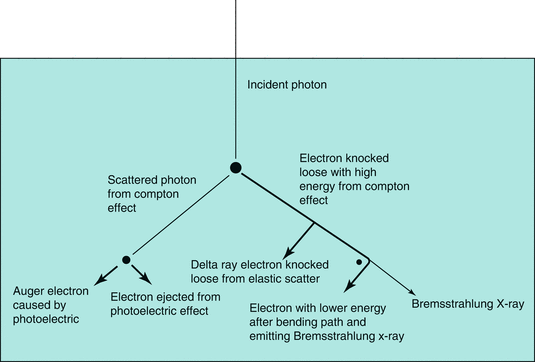
Fig. 6.2

History of an incident photon: In this figure, the path length of photons are thin lines while the path of electrons are heavy lines. In this example, four different electrons and a Bremsstrahlung x-ray are set into motion by a single initial photon. KERMA is the sum of the kinetic energies of these electrons set into motion by the initial photon. All of these secondary electrons will go on to produce ionizations and excitations. The energy deposited by these secondary electrons is dose and the energy deposition will tend to occur deeper than the KERMA transfer.

Kerma → Dose

Photons cause a cascade of electrons (through KERMA) but the electrons do the real ionizing damage (deliver the “dose”).
Since the most important interaction is Compton scatter which generally propel electrons forward, it makes sense that the most damage done by electrons will not be directly at the surface but will actually be slightly deeper.
The depth of greatest damage or “maximal absorbed dose” is d _max. The energy transfer from photons and the dose of energy absorbed are related.
In the buildup region, KERMA is greater than dose. The dose and KERMA curves eventually cross and then descend on a relatively straight linear slope where the curves are parallel but dose is slightly greater than KERMA (Fig. 6.3).

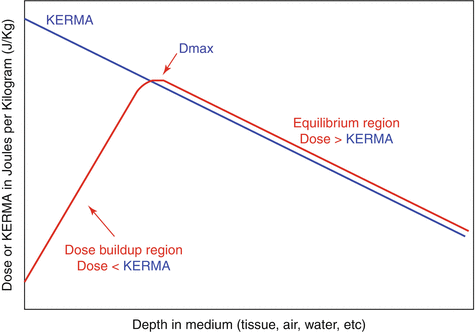
Fig. 6.3

Dose vs. KERMA at depth. After equilibrium dose is always higher than KERMA.
The amount of dose buildup from KERMA is based on the photon energy.
- As photon energy increases, the buildup region also increases and the d_max becomes deeper.
- There is also less dose fall-off with depth (high energies penetrate deeper).
- In general, we describe doses in percentages, in order to make curves that show the percent of dose at depth (PDD). We will discuss this in much greater detail in the chapter on photon dosimetry (Chapt. 9) (Fig. 6.4).
  
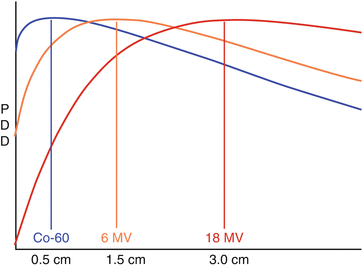
  Fig. 6.4
  
  Percent Depth dose of various photon energy spectrums with extended view of x axis.

Relative Biologic Effectiveness (RBE) (see Chapts. 19 and 22)

Not every joule energy of radiation performs the same amount of damage in a complex cell.
Often measured in Gy equivalent or cGy (cobalt Gy equivalent).
The main damage that kills a cell is a double stranded DNA break.
- Radiation that is more likely to break both strands of DNA at the same time is more efficient at killing with the same amount of absorbed dose.
- If you pack all that energy transfer into one small but powerful explosion and that explosion happens to be very near the DNA double strand, then you are sure to destroy that DNA (Alpha particles, carbon ions, etc.).
  
  Only gold members can continue reading. Log In or Register to continue
  Share this:
  Click to share on Twitter (Opens in new window)
  Click to share on Facebook (Opens in new window)
  Related posts:
  
  Interactions of Electromagnetic Radiation with Matter Special Topics: Hyperthermia and Computers Hyperthermia Carcinogenesis and Heritable Effects Cell Death and Survival Assays Fractionated Radiation Survival Models
  
  Stay updated, free articles. Join our Telegram channel