and Rakhi Kaila2
(1)
School of Physics, University of New South Wales, Sydney, NSW, Australia
(2)
School of Medicine, University of New South Wales, Sydney, NSW, Australia
Abstract
There are no short cuts to science and development. The quantum nature of matter is learnt through the basics of the quantum mechanics (QM). Quantum science education unfortunately at present does not form part of the curriculum at secondary level of education. It is the situation all over the world. Learning QM is no more difficult than learning the Newtonian Mechanics (NM). In NM we are dealing with large rigid bodies; the dynamics is macroscopic in nature and the object’s position, velocity, acceleration etc. can be accurately determined. Further in NM the large objects e.g. planets do not react chemically. The only interaction they have is through the gravitational forces and is very weak. It has little affect on the human life visually to any degree of significance known. Planets in our solar system interact through gravitational forces among each other and with the sun in space and time and keep their dynamics of motion in equilibrium. The forces which make them move and remain in balance are well understood. The motion of the moon under the influence of gravitational forces around earth does however control to some extent the tidal effects and probably the climate on earth as well.
4.1 The Basics
There are no short cuts to science and development. The quantum nature of matter is learnt through the basics of the quantum mechanics (QM). Quantum science education unfortunately at present does not form part of the curriculum at secondary level of education. It is the situation all over the world. Learning QM is no more difficult than learning the Newtonian Mechanics (NM). In NM we are dealing with large rigid bodies; the dynamics is macroscopic in nature and the object’s position, velocity, acceleration etc. can be accurately determined. Further in NM the large objects e.g. planets do not react chemically. The only interaction they have is through the gravitational forces and is very weak. It has little affect on the human life visually to any degree of significance known. Planets in our solar system interact through gravitational forces among each other and with the sun in space and time and keep their dynamics of motion in equilibrium. The forces which make them move and remain in balance are well understood. The motion of the moon under the influence of gravitational forces around earth does however control to some extent the tidal effects and probably the climate on earth as well.
The situation in QM is quite different in many ways but similar in some manner. The electrons orbit around the nucleus very much like in the planetary motion. But the forces involved are of coulomb (charge-interaction) type and much stronger in nature. In an ensemble like the brain they interact chemically through charge transfer, energy transfer, spin transfer, etc. But the dynamics (interactions between them) of the atoms, molecules etc. involved is quantized. What it means is the interactions are a result of exchange of charge, spin, etc. happening in jumps of pockets called as quantum. In quantum dynamics (QD) only some selected values of energy transfer as quantum jumps are allowed. These are based on the laws of the conservation of the angular momentum of the orbiting electron, in an atom. In an ensemble like the brain interactions with the neighboring and distant spins (atomic and molecular magnets) is involved. This is what quantum dynamics is about. The reader is referred to an introductory textbook on quantum physics for more insight into the wonders of the quantum science.
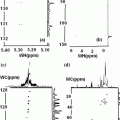
In QD the position, momentum, energy, etc. are not continuous variables. Their values are quantized i.e. they change in fixed quantum jumps. The energy of confinement of the ensemble of molecules is, called as the Hamiltonian of the system and is quantized i.e. it can only change in small quantum jumps. There are energy transitions between different quantum energy levels of the molecules. Also there are quantum correlations between different molecules. The chemical shift due to the varied surrounding electronic environment, J-coupling due to the interaction of the spin (magnetic moment) and angular momentum, etc. are the variable parameters. The position, momentum, energy, etc. in quantum science (QS) like in NM are the tools of the study of the dynamics of spins. Here the position, energy and momentum are, in their order of magnitude scales very microscopic in magnitude, e.g. the distances between molecules are around nm to micrometer scale. The coordinates in space i.e. position and momentum, behave like mathematical operators rather than being continuous analytical (e.g. x, y, z) variables. They operate on an ensemble of atoms, molecules etc. and bring out concrete results. For example, an operator can rotate spins and determine their evolution with time in an ensemble of the molecules. The dynamics of the spins in an ensemble like the brain is dealt in a space of matrices called as the Hilbert space. The size of the space is variable and is given by (2)N × (2)N. Here N is the number of spins and the digit 2 corresponds to the, up and down, two states, of the magnetic spin. For a single spin (N = 1) case the space is of 4 matrices with each matrix having two rows and two columns. In the case of two spin (N = 2) system there will be 16 matrices of size 4 × 4 and so on.
The matrix operators are the basis of the spin dynamics in the brain ensemble. In order to predict the dynamics of the atoms, molecules etc. one uses the mechanics of the matrices. The behavior of the spins can be mapped by using spin matrices as variables in space and time and solving appropriate equations of dynamics of the matrices. In QM, the operators (energy momentum, etc.) do not commute. This means as an example for the position (operator q) and momentum (operator p), in NM, qp − pq = 0. But in QM, qp − pq ≠ 0, instead qp − pq = iħ. The letter i represents a complex number 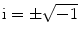 . Here ħ = h/2π and h, is the familiar angular Planck’s constant of the electromagnetic radiation. Those readers who are not familiar, with this complex number need not really bother about it. They only need to remember that this complex number makes the mathematics of the interaction of waves with matter easy to deal with. It is seen that matrices satisfy the same non commutative character as do q and p and other operators in QM. Thus matrices can be used to handle the operators in quantum mechanics. Alternatively one can write the familiar Schrödinger wave equation each time for a system and solve it. This equation is easy to solve for a single atom e.g. hydrogen, helium or a homonuclear ensemble of atoms. For a complicated system like the brain filled with hetero-nuclear species solving Schrödinger wave equation is an impossible task. But matrix mechanics (MM) does allow a reasonable approach and the computer programs are available now to produce prior information and a model image of the brain.
. Here ħ = h/2π and h, is the familiar angular Planck’s constant of the electromagnetic radiation. Those readers who are not familiar, with this complex number need not really bother about it. They only need to remember that this complex number makes the mathematics of the interaction of waves with matter easy to deal with. It is seen that matrices satisfy the same non commutative character as do q and p and other operators in QM. Thus matrices can be used to handle the operators in quantum mechanics. Alternatively one can write the familiar Schrödinger wave equation each time for a system and solve it. This equation is easy to solve for a single atom e.g. hydrogen, helium or a homonuclear ensemble of atoms. For a complicated system like the brain filled with hetero-nuclear species solving Schrödinger wave equation is an impossible task. But matrix mechanics (MM) does allow a reasonable approach and the computer programs are available now to produce prior information and a model image of the brain.
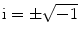 . Here ħ = h/2π and h, is the familiar angular Planck’s constant of the electromagnetic radiation. Those readers who are not familiar, with this complex number need not really bother about it. They only need to remember that this complex number makes the mathematics of the interaction of waves with matter easy to deal with. It is seen that matrices satisfy the same non commutative character as do q and p and other operators in QM. Thus matrices can be used to handle the operators in quantum mechanics. Alternatively one can write the familiar Schrödinger wave equation each time for a system and solve it. This equation is easy to solve for a single atom e.g. hydrogen, helium or a homonuclear ensemble of atoms. For a complicated system like the brain filled with hetero-nuclear species solving Schrödinger wave equation is an impossible task. But matrix mechanics (MM) does allow a reasonable approach and the computer programs are available now to produce prior information and a model image of the brain.
. Here ħ = h/2π and h, is the familiar angular Planck’s constant of the electromagnetic radiation. Those readers who are not familiar, with this complex number need not really bother about it. They only need to remember that this complex number makes the mathematics of the interaction of waves with matter easy to deal with. It is seen that matrices satisfy the same non commutative character as do q and p and other operators in QM. Thus matrices can be used to handle the operators in quantum mechanics. Alternatively one can write the familiar Schrödinger wave equation each time for a system and solve it. This equation is easy to solve for a single atom e.g. hydrogen, helium or a homonuclear ensemble of atoms. For a complicated system like the brain filled with hetero-nuclear species solving Schrödinger wave equation is an impossible task. But matrix mechanics (MM) does allow a reasonable approach and the computer programs are available now to produce prior information and a model image of the brain.4.2 Multi-Dimensional Spin Space and the MRI
The Biological spin systems have been created in nature for some reason. The reason is to sustain life. They (the animal model) shed some important conclusions to explore the model of the human brain. In order to learn first hand about the role of magnetic spins in the evolution of life on earth it is easier to start with some real life illustrations. The spins can be produced and used in a laboratory environment and that is what MRI is about. The virtues of the use of spins as scientific model to predict outcomes in the natural life becomes clear through the following arguments. In a laboratory one can produce a biological quantum computer. Here use can be made of the spin’s up and down the two logic states of the spins. These arise out of the electron’s intrinsic magnetic moment. It also has coupling with atomic and nuclear spin states. This coupling referred to as the J-coupling can be used to connect the two logic states reversibly by applying an RF radiation pulse in a suitable chosen system. One can build the q-bits (termed this way in contrast to the term ‘bit’ used in an electronic computer) and the required quantum logic gates to develop a quantum computer.
There can be a large number of spins (~1023) in a small volume e.g. in 1 mol of a liquid. The enormous power of the quantum computer is thus clear. The dimension of the space required where the spins will work is very large. Manipulation is easy if all the spins are identical. In a natural situation there can be a multinuclear environment e.g. the one we have in our brain. In that case the spins are not-equivalent. The problem is much more complex than imagined. The matrix coordinate space (called as the Hilbert space) provides a good solution to this problem. If all the spins are equivalent, i.e. taken from the same kind of molecules (species) in an ensemble the system is considered as pure. They only need repetition of some basis coordinate basis. Identical spins in a liquid system are a good source to develop a quantum computer. The molecules and atoms are very fluid in their nature in an environment like our brain. They can easily tumble, translate, etc. in space.
It does not take an Einstein to understand that our brain is a biological quantum (parallel) computer. In order to make one in a solid-state situation in a laboratory we can use a pure crystalline environment. Crystals have atoms arranged symmetrically throughout e.g. in a Silicon crystal. The crystalline environment for every atom is identical throughout. What happens to one atom is representative of the whole crystal. The spin scale can be multiplied easily but only mathematically yet. In actual practice the solid state quantum computer is riddled with un-surmountable problems. The situation of manipulating spins can be much more advantageous in an ensemble consisting of identical molecules in a liquid state e.g. a selected suitable chemical solution. MRI provides a good insight into the design of a suitable quantum computer which will work at room temperature. In the liquid state every effective single spin of a molecule (if it has multi-spin character) has a unique character. This character is easily preserved throughout when identical molecules form a concentrated liquid chemical solution.
Each atom (spin) in the molecule has a unique position in its bonding with its neighbors. In a solution the molecules repeat themselves in their coordinated arrangement. The arrangement can be identical and repetitive. This single-molecule spin character can be retained in the solution throughout. A single equivalent spin in a molecule is the unique representation of the whole molecule and thus can be for the whole solution. The number of spins in a molecule can be the core order developed for use in the liquid solution. Their large number can be used to process large amounts of data. There is certainly advantage in using liquid-state rather than the solid-state as the molecules can easily translate, rotate etc. in space in a fluid environment.
The rotation degree of freedom is easily available to the spins in liquid state crystals. This is not the case in the solid-state where the atoms are rigidly fixed in space. They are limited in interactions in space with their neighbors. The reader is referred to the Ref. [1] for details. If the molecular structure is repeated over the whole liquid solution the ensemble is in its purest form and the q-bit manipulation is easy as the molecules are identical. This perfectly ideal system is easy to obtain in a laboratory but not seen in real biological systems. There can be more than one in-equivalent spins present in one molecule and in the whole system. In fact in MRI we do not need pure ensemble. The situation in MRI is very ordered for spins. The variations due to the interactions within the molecules and between the molecules over the different regions of the brain is the source of the image produced. The variations created by the nature are just the ones we are looking for in MRI. Are the spin variations in space and time control the cognitive activities of the brain?
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree