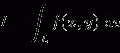(1)
Radiation Monitoring Devices Research Nuclear Medicine, Water town, Massachusetts, USA
2.1 Introduction
2.2.1 Natural Sources
2.5.1 Plants and Vegetations
2.6.2 Detection of Gamma Ray
2.6.3 Detection of X-Ray
2.7.1 Thermal Neutrons
2.7.2 Slow Neutrons
2.8 Boron Reaction
2.9 Lithium Reaction
2.10 Instrumentation
2.10.1 Ion Chamber
2.10.2 Free-Air Ionization Chamber
2.10.3 Proportional Counter (PC)
2.10.6 Geiger–Muller (GM) Counter
2.11 Photomultiplier
2.11.1 Tube
2.12.1 Current Mode
2.12.3 Pulse Mode
2.13.2 Gamma-Ray Spectroscopy
2.13.3 Neutron Spectroscopy
2.13.4 X-Ray Spectroscopy
2.13.7 Measurement of Dose Received
2.13.8 Dosimeters
2.13.9 Commercial Dosimeters
2.13.10 MOSFET Dosimeter
2.13.11 Miniature-Type Dosimeters
2.14.1 The Binomial Distribution
2.14.3 Gaussian Distribution (GD)
2.17 Summary
Abstract
Exposure to Radiation Energy: The materials existing on Earth are exposed to both natural and man-made radiation. Natural background radiation comes from three primary sources: cosmic radiation, external terrestrial radiation, and radon radiation. In addition to these radiations, there are man-made radiations that come from medical X-rays, gamma rays, nuclear medicine, (radionuclides/isotopes), and consumer products [1]. A schematic of the sources of radiation exposure that all the living and the nonliving materials are exposed to is listed below in Fig. 2.1.
2.1 Introduction
Exposure to Radiation Energy: The materials existing on Earth are exposed to both natural and man-made radiation. Natural background radiation comes from three primary sources: cosmic radiation, external terrestrial radiation, and radon radiation. In addition to these radiations, there are man-made radiations that come from medical X-rays, gamma rays, nuclear medicine, (radionuclides/isotopes), and consumer products [1]. A schematic of the sources of radiation exposure that all the living and the nonliving materials are exposed to is listed below in Fig. 2.1.
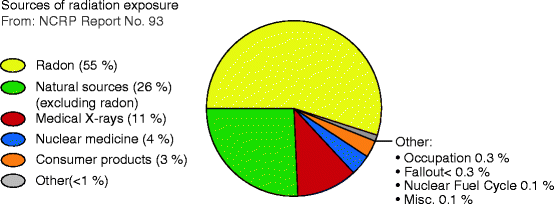

Fig. 2.1
The total percentage of exposure of radiation energy (Courtesy of US EPA, March 2007)
2.2 Sources of Radiation Exposure
2.2.1 Natural Sources
Among the natural radiations that concern most are radon, cosmic radiation, galactic, and solar particles. The alpha (α) radiation emitted by radon is same as the α-radiation radiated from plutonium (Pu). It is a naturally occurring radioactive gas. You cannot see it, smell it, or taste it. The primary routes of potential human exposure to radon are inhalation and ingestion. Humans, particularly in underground and work areas such as mines and buildings, are exposed to elevated concentration of radon and its decay products. The next natural radiation that affects the environment is the galactic and solar particles that have free access to spacecraft outside of the magnetosphere and were identified in early 1960 during the malfunction of the spacecraft electronics.
Figure 2.2 shows EGRET gamma ray surveyed by NASA, USA. Some galactic cosmic rays interact with the interstellar medium and produce gamma (γ) rays [2]. The terrestrial and cosmic rays induce single events and produce an annual dose equivalent to 3.1 millisievert (mSv) [3, 4]. Table 2.1 shows the list of the radiation sources that affect the environment and the surrounding.
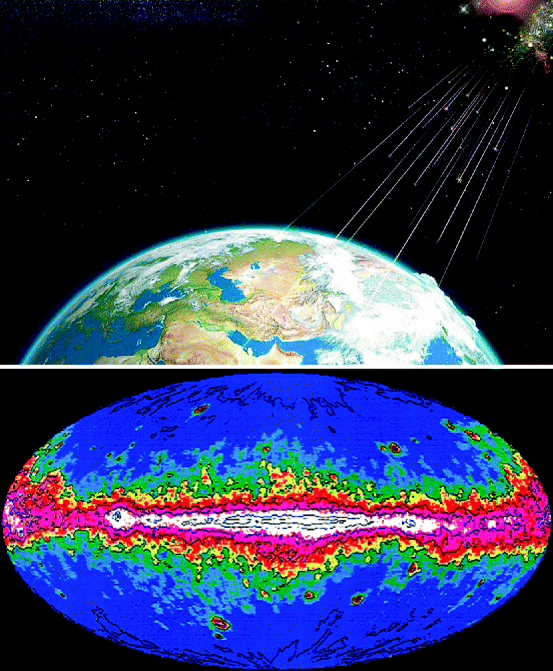

Fig. 2.2
Galactic cosmic ray (GCR), a source of terrestrial gamma-ray radiation (Photo courtesy of NASA USA)
Table 2.1
Annual dose from ground radiation
Source | Type | Annual dose (mSv) |
|---|---|---|
Terrestrial | Natural | 0.26 |
Inhaled radionuclides | Natural | 1.0 |
Internal radionuclides | Natural | 0.26 |
Cosmic radiation | Natural | 0.28 |
Cosmogenetic radionuclides | Natural | 0.01 |
Medical diagnostic | Man-made | 0.92 |
Atmosphere weapons testing | Man-made | 0.05 |
Airline travel | Natural | 1.6/crew, 0.3/passenger |
Consumer products | Man-made | 0.04 |
Nuclear power | Man-made | <<0.01 |
Levels of natural or background cosmic radiation, however, can vary greatly from one location to another depending on the altitude. The biological effects due to natural or background cosmic radiation are so small that they may not be counted for.
2.3 Biological and Related Effects of Radiation
The commercial, industrial, and medical activities contribute about 310 mrem to our annual radiation exposure. It has been estimated that there is a continuous release of ~200-MeV energy per fission that results during the generation of electricity from the chain reactions of uranium-235 (U235). To understand the biological effects of radiation, we must first understand the difference between ionizing and nonionizing radiation [5–7]. Ionizing radiation (shorter wavelengths) being absorbed experiences sufficient energy to disrupt and separate electrons from atoms (Fig. 2.3) and produces ions with a net electric charge. Nonionizing radiation (longer wavelengths), on the other hand, has energy to excite atoms, or electrons, but not sufficient to remove electrons from their orbits or to cause the formation of ions [8].
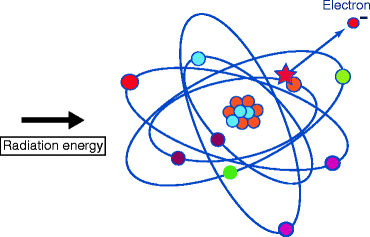

Fig. 2.3
Energetic ionizing radiation and the detachment of an electron from an atom
As the threshold for ionization lies somewhere in the ultraviolet region of the electromagnetic spectrum, we can consider all X–rays and gamma (γ) rays as ionizing radiation. At the same time, we have observed that all forms of nuclear radiation are ionizing radiation because of their extremely high energy. When the tissues absorb radiation, excitation occurs immediately, and for higher-energy radiation, we can expect removal of an electron from an atom or molecule [9, 10].
Living tissue contains about 70–90 % water by weight. When the radiation energy exceeds 1,216 kJ/mol, it can ionize the water molecule (H2O H2O+ + e−) forming free-radical ion which contains an unpaired valence shell electron [11]. The radicals formed during ionization are strongest oxidizing agents. At the molecular level, these oxidizing agents destroy biologically active molecules by either removing electrons or removing hydrogen atoms. This will lead to the damage of the membrane, nucleus, chromosomes, or mitochondria [12, 13].
Radiation of various energies from X-ray and γ-rays produces alpha (α) particles, beta (β) particles, neutrons (n) and photons (p). These α, β, n and p can interact with complex molecules such as proteins and nucleic acid (NA). Radiation sources having sufficient energy can fracture the molecule and prevent their proper functioning. Fast neutrons, however, collide with light nuclei present in the living cell and produce indirect ionizing radiation [14]. This can result in loss of cell vitality, decreased enzyme activity, initiation of cancer, and genetic mutations depending on the energy of the radiated particle [15, 16]. Figure 2.4 shows the schematic of a healthy cell and the effects of radiation on the healthy cell.
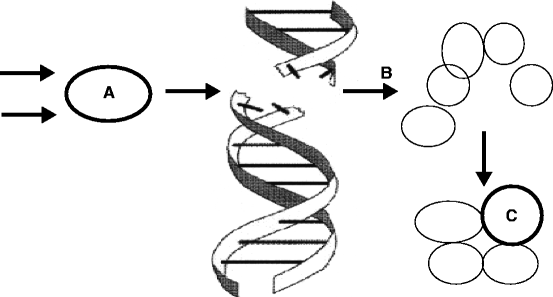

Fig. 2.4
The ionization radiation can damage a healthy cell (A) and can produce a cancerous cell (B), which can ultimately turn into a tumor (C)
Not all forms of radiation have the efficiency for damaging biological organisms. The energetic initial radiation loses energy as it passes through the tissue and causes more damage. As for example, when the energy of the radiation is more than 100 Gy (1 Gy = 100 rad = 1 J/kg), it affects the central nervous system, resulting in loss of coordination (including breathing problems), with death occurring within 1 or 2 days. When the dose ranges from 9 to 90 Gy, it can damage the gastrointestinal tract causing nausea, vomiting, and diarrhea. Even low doses (2–8 Gy) can damage bone marrow and other hematopoietic tissues [17]. It is expected that the research community, the physicians, and the manufacturers should be aware of the competitive issue—the dose. The exposure rate constant (A S) for some common radioisotopes is given below (in Table 2.2, in general terms).
Table 2.2
Exposure rate constant for some common radionuclides γ-ray sources
Radionuclide | Exposure rate constant (R-cm2/h mCi): (As) |
|---|---|
Antimony (124Sb)-124 | 9.8 |
Cesium (137Cs)-137 | 3.3 |
Cobalt (57Co)-57 | 0.9 |
Cobalt (60Co)-60 | 13.2 |
Iodine (125I)-125 | ~0.7 |
Iodine (131I)-131 | 2.2 |
Manganese (54Mn)-54 | 4.7 |
Radium (226Ra)-226 | 8.25 |
Sodium (22Na)-22 | 12.0 |
Sodium (24Na)-24 | 18.4 |
Technetium (99mTc)-99m | ~0.7 |
Zinc (65Zn)-65 | 2.7 |
Different parts of the mammal’s body have different mass, size, shape, and compositions. As a result, the attenuation characteristics and the distribution of the radionuclide will not be uniform throughout the whole body or different organs of the body. At the same time, the ionization density to biological material when exposed to X-rays or gamma (γ) rays is quite low compared to the exposure to neutrons, protons, or alpha (α) particles. Therefore, in order to identify the radiation biological effectiveness (RBE), a second unit of absorbed dose has been defined as the roentgen equivalent man (rem). It is defined as the absorbed dose in rad times the RBE of radiation (rem = rads × RBE) [18, 19]. Table 2.3 shows the values for the radiation biological effectiveness (RBE) of different forms of radiation.
Table 2.3
The radiation biological effectiveness (RBE) of various forms of radiation
Radiation | RBE |
|---|---|
X-rays and gamma rays | 1 |
Electrons | 1 |
Particles with energies < 0.03 MeV | 1 |
Particles with energies > 0.3 MeV | 1.7 |
Slow-moving thermal neutrons | 3 |
Fast-moving neutrons or protons | 10 |
Alpha (α) particles or heavy ions | 20 |
Neutrons (energy dependent) | 5–20 |
All cells are not equally sensitive to radiation exposure. In general, the cells that produce blood are more sensitive to irradiation even at a very lower dose. An acute radiation dose (10 rad or higher to the whole body) can cause a pattern of clearly identifiable symptoms (syndromes), and the condition is called an acute radiation syndrome. As for example, the effect of radiation to the tumors and normal tissues is the result of reactive oxygen species (ROS) and reactive nitrogen oxide (NO) species (RNOS) generation. Hydroxyl (−OH) radical is the most reactive species in vivo that contributes to the peroxidation of lipids and nucleic acids following radiation therapy [20].
From the above biological effects of radiation on mammals, we can categorize biological effects in two sections: (1) deterministic and (2) probabilistic. The first one is generally the reduction of blood cells, skin reddening and blistering, induction of sterility, etc. These arise out of massive cell damage or cell killing due to exposure of the biological system to ionizing radiation.
The second category of the biological effect is known as stochastic effect, and it results from the mutagenic action of ionizing radiation, which can lead to the loss of control over the cell division. It eventually results in the induction of cancer as a result of mutagenic disturbance [21, 22]. On the other hand, if it happens to be a germ cell, the mutated information can be passed on to the progeny leading to genetic effects.
Ionizing radiation thus can cause mutation either by directly affecting the deoxyribonucleic acid (DNA) or indirectly by producing active chemical species in its vicinity, which can affect DNA—a double–standard helical macromolecule present in chromosomes inside the nucleus (Fig. 2.10). In simpler term, nucleic acid is a linear polymer of nucleotides connected by phosphodiester bonds [23].
So far, we have discussed the dark side of the radiation. As a matter of fact, radiation, like other aspects of nuclear science, can both be destructive and beneficial. Some of the intelligent uses of radiation that are beneficial to human being are treatment of cancer, medical diagnosis, and food preservations.
Figure 2.5 shows a simplified two-dimensional diagram of DNA. It has been identified that a prominent cause of DNA damage is its exposure to radiation. The ionizing radiation simulates the cell to form pyrimidine dimer, most frequently between adjacent thymine bases in the same DNA strand, and results cross-linkage of the molecule. However, it is possible to repair various kinds of DNA damage. But, if the human being is mutant in the ability to perform radiation repair, he/she can suffer from a disease known as xeroderma pigmentosum [24].
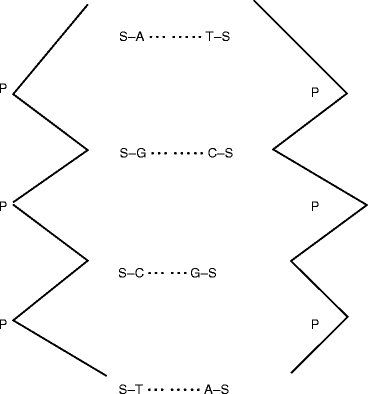

Fig. 2.5
Schematic of a simplified two-dimensional structure of DNA. S sugar, P phosphate, A adenine, G guanine, C cytosine, T thymine
Radiation-induced gnomic instability (RIGI) is a delayed, long-lasting effect of ionizing radiation. What initiates RIGI and the cause that makes it to persist over time is unknown. However, it is presumed that the potential mechanism of RIGI is the oxidative stress caused by a high level of reactive oxygen species (ROS). Experimental observations reveal that increased ROS level in different radiation-induced genomically unstable cell system is the cause of RIGI [25, 26]. Figure 2.6 shows a model for the role of mitochondria in RIGI.
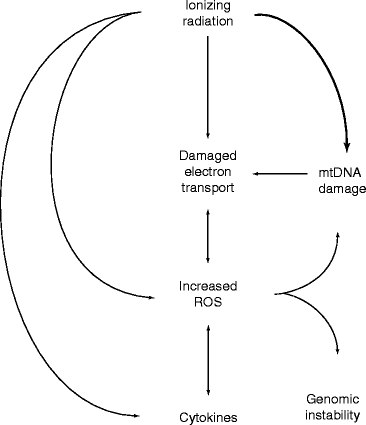

Fig. 2.6
A model for the role of mitochondria in RIGI (Kim et al. Permission from Oxford University Press)
In the last 35 years, a lot of research has been focused on the effects of low-level radiation. But many of the findings have failed to establish the so-called linear hypothesis. However, some evidence suggests that there exists a threshold below which no harmful effects of radiation occur. As a matter of fact, the issue of low radiation and its effect on any increase in cancer modality has become very controversial.
For creatures, exposure to nuclear radiation can cause loss of hair, abnormal growth of thyroid, fatigues, and drop in the number of red blood cells. Although radiation may cause cancer at high doses and high dose rates, public data regarding low levels of exposure below about 1,000 mrem (10 msv) are harder to interpret. However, light radiation sickness begins at about 50–100 rad (0.5–1.0 gray (Gy), 0.5–1.0 sv, 50–100 rem, and 50,000–10,00,000 mrem) [27, 28].
Figure 2.7 shows the effect of radiation on humans being exposed to a 15-megaton bomb that exploded at a test site 100 miles apart from Marshall Islands, Bikini, north of the equator in the western Pacific Ocean, on March 1, 1954.
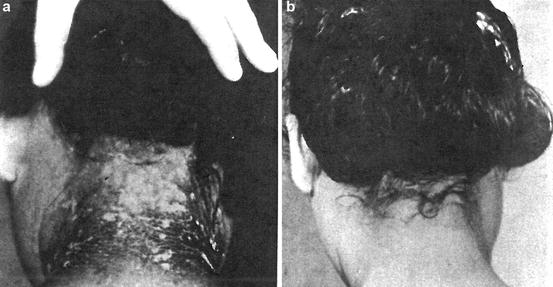

Fig. 2.7
(a) Twenty-eight days after exposure to beta particle and (b) after recovery (Courtesy of Armed Forces Institute of Pathology)
In order to meet the criteria and the health and safety regulations, the public and the people working with radioactive materials and in the nuclear plants should be aware of the facts that proper treatments, conditioning, and final disposal of the wastes must be carried out cautiously. Radiation exposures during normal operations are to be considered in two parts: (1) exposures to occupational workers and (2) exposures to environment. Therefore, as a safety measure, the detection of the amount of exposure to the ionization energy is essential [29, 30].
2.4 Effects of Radiation on Consumable Products
People should be aware of the facts that certain foods such as bananas and nuts contain higher levels of radiation than other foods. Other consumer products that may be the source of radiation are toys and certain types of cosmetics, like hair products, contact lens solution, removing irritants, and allergens. Smoke detector is also a source of radiation, which uses americium-241 in gold matrix. During sterilization of the bandages and the surgical instruments, radiation sources are used. The last but not least, the people should know that the brick and stone homes have higher natural radiation levels than homes made of other building materials such as wood.
2.5 Effects of Radiation
2.5.1 Plants and Vegetations
So far, we have discussed mostly about the biological effects of ionizing radiation on living animals in context of human species. But when we are talking about the effect of ionizing radiation on the environment and the surrounding, we must consider the plants and vegetations that are part and parcel to our environment. An obvious question would be: How the ionizing radiation affects the plants and the vegetations that constitute the major part of the environment? Real and his coworkers [31] have reported a comprehensive review on the effects of ionizing radiation exposure to plants, fish, and mammals.
Figure 2.8 shows radiation effects on plants in a field near Pripyat in the Ukrainian Soviet Socialist Republic. On April 26, 1986, reactor number four at Chernobyl Nuclear Power Plant near Pripyat in the Ukrainian Soviet Socialist Republic exploded. The plume drifted over extensive parts of Western Soviet Union, Eastern Europe, Western Europe, Northern Europe, and eastern North America with light nuclear rain falling as far as Ireland. After the disaster, three square miles of pine forest in the immediate vicinity of the reactor turned ginger brown and died, earning the name of the Red Forest [32–34].


Fig. 2.8
Radiation effects on plants in a field near Pripyat in the Ukrainian Soviet Socialist Republic (Photo courtesy of Wikipedia)
Effects of ionizing radiation on plants and animals are considered at two levels: (1) on the individual and (2) on the population [35]. The population effect arises from the individual effects, and it is only the statistical aspect, which is important at the population level. For plants, population effects are loss of foliage, reduced growth, and loss of reproductive ability and ultimate extinction of the species. In the case of animals, it is generally considered on the basis of the health and overall survival of the animals suffering from chronic diseases.
Higher plants, which are more sensitive to radiation, are affected by ionization energy less than 10–1,000 Gy. Extensive studies on pine-birch forests have shown that trees of the same species and age have different dose sensitivities depending on external conditions such as light interception, soil fertility, and wind erosion. For example, several studies on the general threshold in the oak–pine forest at Brookhaven have shown that approximately 0.5 Gy/day (d) is detrimental to the trees. Most of the species are found to be affected when the radiation label reaches approximately 3 Gy/d. Several plants such as algae, fungi, and symbiotic lichens are resistant to gamma-ray radiation. However, older plants and mostly the woody species are seen to be affected with a dose of 10 Gy/d or more. The Erigeron canadensis are seen to show detrimental effects at 6.4 Gy/d, where most of the Mediterranean species are found more resistant to ionizing radiation. However, the sub-Mediterranean species are not as much resistive to ionizing radiation compared to the Mediterranean species. Deserts shrubs are seen to be affected when the ionization goes beyond 0.001–0.1 Gy/h and above 0.07 Gy/d are seen to be detrimental to all vegetation.
It has been found that gamma radiation produces enhanced protease activities in some seeds like peanut and wheat and induces oxidative stress, which damages the protein quantity of the seeds. Gamma radiation also damages the enzyme of the citrus fruits when the dose exceeds 15 Gy. Considering reproductive viability, even though the size and rate of pollen are temporarily affected with a low dose of 0.7 Gy/d, they get restored within 3 years for irradiation up to 12 Gy [36].
From the studies of the radiation exposure and the consequences that are so far presented, it seems that mammals are the most sensitive to ionizing radiation, and a dose of 5–15 Gy can be lethal dose to them. At the other extreme are the bacteria and protozoa that are affected with a dose ranging from 103 to 104 Gy. Classical Andrews lymphocyte depletion curves (1–4) and accompanying clinical severity ranges correspond roughly the following graph (Fig. 2.9) [38]:
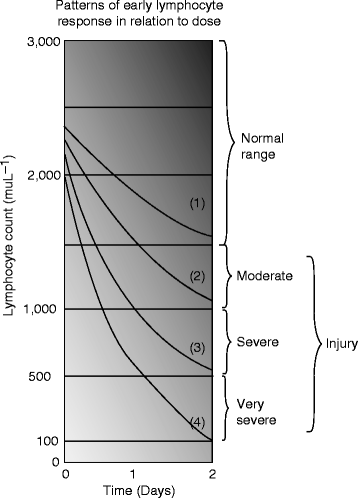

Fig. 2.9
Classical Andrews lymphocyte depletion curves. Curve 1–3: 1 Gy, curve 2–4: 4 Gy, curve 3–4: 6 Gy, and curve 4: 7.1 Gy (Courtesy: R. Goans, ORAU)
Table 2.4 shows the comparative radiosensitivity of groups of organisms.
Table 2.4
Comparative radiosensitivity of groups of organisms
Group | Lethal dose (range) in rad |
|---|---|
Bacteria | 100,000–1,000000 |
Insects | 5,000–1000,000 |
Fish | 1,000–3000 |
Mammals | 300–1200 |
Herbaceous plants | 5,000–70,000 |
Coniferous trees | 800–3000 |
Deciduous trees | 4,000–10,000 |
2.5.2 Electronics and Associated Active and Passive Elements
Besides being its detrimental effects on health of the living cells and tissues of creatures, nuclear radiation induces defects in several semiconductor devices and electronics leading to enhanced generation/recombination currents. As a result, charge collection signal is reduced, and there is a drift in operating point.
The vertical primary population intensities of galactic cosmic rays (GCR) and solar particles affect the electronics of the spacecraft. As a result, military space electronics require special technology to study the primary population intensities of GCR and solar particles that cause variations in secondary neutron and proton levels [2]. During irradiation, the incident particles collide with the nucleus and transfer part of the energy. Experimental observations show that there is an exact linear relationship between ionizing energy deposited by the incident particle in lattices of the semiconductor materials and the measured degradation [39]. However, long-term exposure to ionizing energy results in nonlinearities, and these complicate the determination of displacement damage factors.
Radiation-induced defects in silicon (Si)- and germanium (Ge)-based junction devices (e.g., CMOS, bipolar transistors, photodiodes) are well established [40, 41]. Irradiated energetic particles incident on the device lose their energy to ionizing process and result in the production of electron–hole pairs and displaced atoms. The effectiveness of the radiation-induced displacement damage depends upon the bombardment conditions and on the time after irradiation [42]. A key theme that emerged from all these studies by various workers suggests that the effects on electrical properties of the semiconductor materials depend on the irradiated rays (fission or neutrons or gamma rays) [43, 44].
As a matter of fact, the metal oxide semiconductor (MOS) technology, particularly complimentary MOS (CMOS) technology, which is the dominant commercial technology, has been severely affected by ionizing radiation [27, 28]. On the other hand, silicon–on–insulator (SOI) technology has been developed for radiation-hardened applications for many years. However, bipolar amplification caused by floating body effects can significantly reduce the single-event upset (SEU) hardness of SOI devices [29].
In bipolar junction transistors (BJTs, npn, and pnp), current gain is noticed when base emitter junction is irradiated [30, 31]. Earlier study by Goben demonstrated the damage in bipolar transistor by neutrons [32].
Many medical modalities like computer tomography (CT), positron emission tomography (PET), single–photon emission tomography (SPECT), magnetic resonance imaging (MRI), and ultrasound are inherently digital. These digital technologies offer significant improvements in image quality and dose utilization [33]. However, most of these digital circuitry (flat–panel detectors (FPD), charge–coupled devices (CCD), and thin–film transistor (TFT) array) used in medical imaging system are based on solid-state integrated circuit (IC) technology, similar in many ways to the imaging chips used in visible wavelength digital photography and video [45]. These photonic imagers are also being used in space systems, where they are exposed to space radiation environment. Ionizing radiation during X-ray and γ-ray exposure affects the normal behavior of these devices [46].
Aerospace is involved in collaborative research efforts to study the novel approaches for hardening commercially available integrated circuits (ICs) against single-event latch-up. The picosecond laser facility is also being used to study the effectiveness of various design strategies for mitigating the effects of single-event transients in digital electronic circuits. Figure 2.10 shows the use of a large-diameter laser beam allowing for rapid identification of regions of complex integrated circuits (ICs) that are susceptible to single-event effect.


Fig. 2.10
A large-diameter laser beam that allows for rapid identification of regions in complex integrated circuits (ICs) that are susceptible to single-event effects (Photo courtesy of Crosslink, The Aerospace Corporation, CA)
It has been observed that when a cosmic ray passes through the drain region of an NMOS transistor, a short circuit is momentarily created between the substrate (normally grounded) and the drain terminal (normally connected to the positive power of the supply voltage) resulting a spike of current. The amount of charge that is collected from the ion track can burn out the device or may cause malfunctioning of the device. Figure 2.11 shows the path of the cosmic ray through the drain of an NMOS transistor.
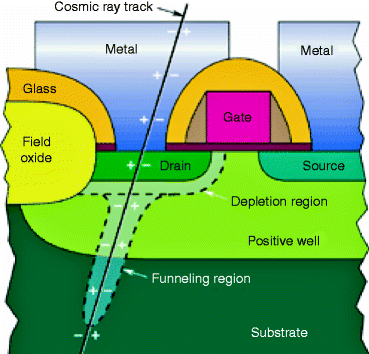

Fig. 2.11
The path of a cosmic ray through the drain of an NMOS transistor (Courtesy of Cross-link, The Aerospace Corporation, CA)
During 1990s, many groups were involved in studying the radiation effects in charge-coupled devices (CCDs, arrays of MOS capacitors) including CMOS [47] thin-film transistors (TFTs), passive pixel arrays such as charge-induced devices (CID), photodiodes (including avalanche), infrared (IR) detectors, and other semiconductor devices that are being used in space program or in medical imaging system [48–51].
High dose of irradiation causes radiation damage and general alteration of the operational and detection properties of a detector (scintillator). There are three main aspects of radiation stability in plastic scintillator such as polymer hardness (optical stability), dopant stability, and stability in fiber waveguide structures. The amount of light intensity losses in the scintillator (which is a bulk effect of the polymer) depends on the dose and the building material of the scintillator. The light yield loss and the transmittance loss in plastic scintillators are about ~20 % and 2–6 %, respectively, for a dose of 105Gy [52]. In scintillation fibers, radiation degrades scintillation core, polymer cladding, and core/cladding interface [53]. On the other hand, garnet-containing inorganic scintillators of terbium (Tb) and lutetium (Lu) show increased resistance to radiation damage until the dose reaches 105Gy or higher [54].
2.6 Detection of Radiation
Ionizing radiation is ubiquitous in the environment and also comes from radioactive materials, X-ray tubes, and particle accelerators. It is invisible and not directly detectable by human senses. Therefore, instrument for the evaluation of minimum levels of delectability is of prime interest. As a matter of fact, nuclear detection is always a multistep, highly indirect process. For example, in a scintillation detector, incident radiation excites a florescence material that de-excites by emitting photons of light. The light is focused onto the photocathode of a photomultiplier (PMT) tube that triggers an electron avalanche. The most common handheld or portable instruments are ionization chamber, proportional counters, Geiger counter, optically simulated luminescence (OSL) dosimeters, and multichannel analyzer system.
Four major forms of radiation are commonly found emanating from radioactive matter: alpha (α), beta (β), gamma (γ), and X–ray radiation. Alpha particles, the heaviest and the most highly charged of common nuclear radiation, are the most difficult to detect. Since these particles can easily be trapped by other materials, quantitative measurement of alpha radiation is impossible outside of a laboratory environment. The field instruments, such as the AN/PDR-56, AN/PDR-77, and ADM-300, use an extremely thin piece of aluminized Mylar® film on the face of the detector probe. It has been found that counting efficiencies of these alpha detectors are between 20 and 60 %.
2.6.1 Detection of Alpha (α) and Beta (β) Particles
Beta particles are energetic electrons emitted from the nuclei of many natural and man-made radioactive materials. Low-energy beta particles are less penetrating than the alpha particles, requiring special techniques for detection. From the detection standpoint, unfortunately, high-energy beta and gamma radiations are not the primary decay products of the most likely radioactive materials. Rather, the major potential source of beta and/or gamma radiations is from fission products.
Alpha (α) and beta (β) particles are detected and measured by ionization chamber. Absolute measurements of (α) particle are straightforward and involve evaluation of the effective solid angle subtended by the counteractive volume (which is close to 2π for initial source flow counts). On the other hand, absolute (β) activity measurements are often carried out in a 4π flow counter. When both alpha (α) and beta (β) particles are present in the emitting source, the spectra of α- and β-particles will be different [55–57]. The β-spectrum is generally broader and shorter in pulse height. The corresponding count curve will show two distinct plateaus: In the first plateau, αs are counted, and in the second, both αs and βs are counted. It has been observed that the beta plateau is generally shorter and shows a greater slope than alpha plateau. The obvious reason is that the beta particle pulse height distribution is broader and less well separated from the low-amplitude noise.
Figure 2.12 shows the spectra of alpha and beta particles, when the pulse height (H) is plotted against differential number of pulses within the differential amplitude increment (dN/dH). The right-hand-side curve shows the plateaus when counting rate is plotted against the applied voltage (V).
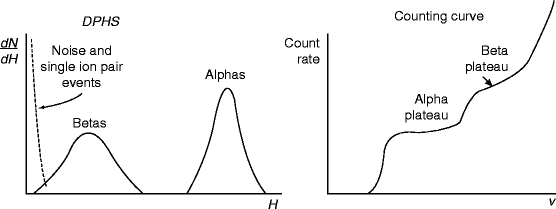

Fig. 2.12
The spectra and plateaus of alpha and beta particles (Reprinted with permission Wiley)
Experimental detection of α-particles from the radioactive decay of natural bismuth (209Bi) has been reported by P. de Marcillac et al. [55]. They have detected an energy release of 3,137 ± 1 (statistical) ± 2 (systematic) keV and a half-life of (1.9 ± 0.2) ~ 1,019 years, which are in agreement with expected values. It has been observed that the nuclear structure of naturally occurring 209Bi isotope gives rise to an extremely low decay probability and it generates low-energy particles that are difficult to detect. Therefore, their detection has no quantitative use but is used as a safety precaution.
2.6.2 Detection of Gamma Ray
The key process of detecting gamma ray is by ionization. During ionization, it gives up part or all of its energy to an electron. The energized electrons then collide with other atoms and liberate electrons. The liberated charge is collected either directly, using gas ionization type (ion chambers, proportional counters, or Geiger–Muller (GM) counters) counters, or indirectly (as with scintillation detector), in order to record the presence of gamma ray and measure its energy. Details of these counters and the scintillators will be discussed later.
2.6.3 Detection of X-Ray
X–rays are emitted by electrons outside the nucleus, while gamma rays are emitted by the nucleus. To detect X-rays, we can use either a photographic plate or photostimuable phosphor. Proportional counters are the most common X-ray detectors used, although CCD chips are rapidly gaining popularity. Besides, Geiger counter based on the ionization of gases is also being used.
Scintillators like NaI:Tl can convert X-ray photons into visible photons and can be detected by a photomultiplier tube (PMT). Other solid-state direct detectors like lithium-doped silicon (Si(Li)) and lithium-doped germanium (Ge(Li)) have also been used to detect X-rays. However, detectors like CdTe, CZT, and HgI2 have also been used to detect X-rays. Recently, these materials are deposited on a TFT array or flat-panel array for medical imaging using X-rays.
2.7 Neutron Detection
The process of neutron detection begins when neutrons, interacting with various nuclei, initiate the release of one or more charged particles. Two basic types of neutron interactions with matter are available: recoil type and interaction type. Recoil-type counters measure only the first interaction event. Reaction type, however, takes advantage of the increased reaction probability at low neutron energies by moderating the incoming neutrons.
Neutron is electrically neutral. Its temperature is called the neutron energy, or a free neutron’s kinetic energy, usually measured in electron volts (eV). Kinetic energy (KE), speed, and wavelength of the neutron are related to the de Broglie relation and are classified according to the distribution of the energies. As for example, a slow neutron has energy less than or equal to 0.4 eV, whereas the fast neutrons have energy greater than 0.1 eV [58, 59]. When a neutron has energy of about 0.025 eV, it is identified as thermal neutron.
Advances in materials and methods have enabled the detection of neutrons with cryogenic neutron detectors to room-temperature semiconductor detectors [60–62]. A cryogenic neutron detector operates by detecting the heat pulses caused by neutron capture and scattering [37, 63, 64]. On the other hand, a semiconductor detector is able to detect neutrons from a neutron-sensitive material like uranium oxide boron, lithium, or polyethylene on aluminum layer, placed in contact with silicon diode or a GaAs detector, which finally detects the nuclear reaction products [65–67]. However, coated detectors are seen to suffer from a lack of sensitivity [68].
Gupta, Schieber, and Knittel et al. [69–71] have reported the results for a number of inorganic scintillators fabricated from various combinations of inorganic elements like Gd, B, and Li. On the other hand, Chung and Chen [72, 73] have described a method where they have used a germanium (Ge) detector where reactions of neutrons with 72, 74 Ge (n, n’, γ) produce gamma (γ) rays at 596 and 691 keVs to detect gamma rays. A new-type polycrystalline CVD (chemical-vapor-deposited) diamond detector with high gain for neutron detection has been reported [74–76]. Use of a dosimeter for the detection and measurement of neutrons has also been reported by Angelone et al. [77, 78]. Detectors have also been fabricated from compounds of inorganic materials like Li2B4O7 and BaB4O7 to study neutrons [79]. Siffert et al. on the other hand had exploited CdZnTe (CZT) and CdTe to study thermal neutrons [80].
Some organic scintillators consisting of phosphors are prepared by dissolving (generally) the phosphor in a hydrocarbon plastic like polystyrene or polyvinyl toluene or in liquid such as benzene, xylene, or toluene and have been used to detect neutrons. The hydrocarbon matrix with phenyl ring provided by the phosphor helps to hop the deposited ionization energy from one ring to another until it finally transfers to a phosphor molecule. In many cases, silicon rubber (Si–O–Si) [81, 82] has been used as a suitable matrix. Recently, anthracene and stilbene have achieved widespread popularity as pure organic scintillators for neutron detection [83]. At the same time, semiconducting polymers (such as poly tri-aryl amine) have offered many advantages as organic detectors over their conventional inorganic counterpart for detection and measurement of neutron [84, 85].
2.7.1 Thermal Neutrons
Thermal neutrons are used in nondestructive testing (NDT) because of their advantages over X-ray and gamma-ray testing [86, 87]. As a matter of fact, NDT testing by thermal neutrons provides complementary information about the interactions of photons and neutrons with matter. Photons interact with the atomic electrons, while neutrons interact with the atomic nucleus itself. Neutrons can penetrate into the high-density materials that are opaque to X-rays thus allowing the inspection of objects obstructed by a dense material. Moreover, the attenuation of thermal neutrons (relative to X-rays) is pronounced for lighter elements such as hydrogen, carbon, and their compounds that comprise the base for many organic materials. The nuclides that are frequently used for thermal neutron detection are helium (He3), lithium (Li6), boron (B10), cadmium (Cd113), and gadolinium (Gd155 and Gd157) [88–90].
2.7.2 Slow Neutrons
The energy of a slow neutron is extremely low (energy below the cadmium cutoff of about 0.5 eV) with the reaction Q-value, and it loses its initial kinetic energy (KE) during conversion process. Slow neutrons are detected through nuclear reactions which result in energetic charged particles such as protons and alpha (α) particles [91]. The neutron detectors are composed of two detectors—the target detector and the detector for detection and measurements. Since cross section for neutron interactions in most materials is a strong function of the energy of the incoming neutrons, different techniques have been developed to detect and measure neutrons in different energy regions. For the detection and measurements of slow neutrons in an efficient way, we have to consider several factors:
1.
The cross section for the reaction must be very large, especially when the target material is incorporated as gas.
2.
The target nuclide should either be of high isotopic abundance in natural element or artificially enriched sample.
3.
The detection process should be able to discriminate gamma (γ) rays.
4.
Q-value of reaction should be large.
2.8 Boron Reaction
Boron 10B (n,α) has been identified as a popular reaction material for the conversion of neutrons [92, 93]. The reactions that followed due to the reactions of the slow neutron and the target material are as follows:
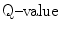
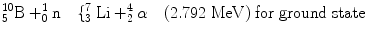
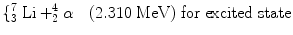
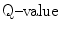
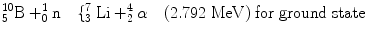
(2.1)
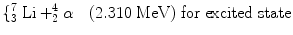
(2.2)
When the incoming neutron is a thermal neutron (E n = 0.025 eV), 94 % of all reactions lead to the excited state [94, 95]. The Q-value of reaction becomes very large between 2.310 and 2.794 MeV compared to the slow neutron, and the reaction product is 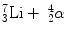 . The energy of the individual product can be calculated from the conservation of energy and momentum as
. The energy of the individual product can be calculated from the conservation of energy and momentum as
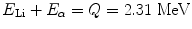
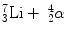 . The energy of the individual product can be calculated from the conservation of energy and momentum as
. The energy of the individual product can be calculated from the conservation of energy and momentum as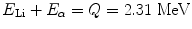
(2.3)
The momentum p (product of mass m and velocity v) of lithium is equal to the momentum (p) of alpha particle, that is, p Li = p α. So we can write (2m Li E Li)1/2 = (2m α E α)1/2. From these equations, we can get the values of E Li = 0.84 MeV and E α = 1.47 MeV. The thermal neutron cross section for 10B (n, α) reaction is 3,840 barns. The cross-section value drops rapidly with increasing neutron energy and is proportional to (1/v).
2.9 Lithium Reaction
The reaction between slow neutron and lithium (Li) is as follows:
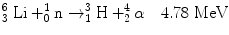
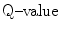
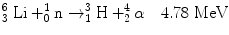
(2.4)
Similarly following the equations presented with boron reactions, we can arrive to the values of 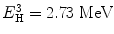 and E α = 2.05 MeV. The thermal neutron cross section for
and E α = 2.05 MeV. The thermal neutron cross section for 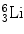 is 940 barns. Recently, commercially available pyrolytic boron nitride (BN) (5-mm2 area and 1 mm thick) coated with an epitaxial layer of GaAs has been used as thermal neutron source [96].
is 940 barns. Recently, commercially available pyrolytic boron nitride (BN) (5-mm2 area and 1 mm thick) coated with an epitaxial layer of GaAs has been used as thermal neutron source [96].
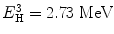 and E α = 2.05 MeV. The thermal neutron cross section for
and E α = 2.05 MeV. The thermal neutron cross section for 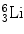 is 940 barns. Recently, commercially available pyrolytic boron nitride (BN) (5-mm2 area and 1 mm thick) coated with an epitaxial layer of GaAs has been used as thermal neutron source [96].
is 940 barns. Recently, commercially available pyrolytic boron nitride (BN) (5-mm2 area and 1 mm thick) coated with an epitaxial layer of GaAs has been used as thermal neutron source [96].Gas–filled detectors are used to detect either thermal neutrons via nuclear reactions or fast neutrons via recoil interactions. Gas-filled detecting chambers typically employ 3He, 4He, BF3, or CH4 as the primary gases, at a pressure varying from less than 1 atm to about 20 atm depending on the application. As neutron detectors are also sensitive to gamma ray, therefore, the gamma-ray sensitivity of a neutron detector is an important criterion in its selection.
2.10 Instrumentation
The instruments that are used to detect the ionizing radiation are based on ionization of the gas inside a chamber, and they are categorized as (1) ion chamber, (2) proportional counter, and (3) Geiger tubes.
2.10.1 Ion Chamber
The instrument, in principle, is the simplest of all the gas-filled detectors, where ions are formed by direct ionization and measured by the application of electric field. Unlike proportional counter and the Geiger tubes that are operated in pulse mode, ion chamber is operated either in current mode or pulse mode [97, 98].
Figure 2.13 shows the picture of an ionization chamber, which is an electrically closed vessel containing an internal electrode.


Fig. 2.13
The picture of an ionization chamber (Photo courtesy of Overhoff company)
Working Principle: Ions are formed in the gas chamber either by direct interaction with the incident particle or through a secondary process in which some of the particle energy is first transferred to an energetic electron. Experimental observation shows that when a particle having energy of 1 MeV is stopped within the gas, it creates almost 30,000 ion pairs. The deposited energy is proportional to the number of ion pairs formed provided the average energy lost by the incident particle per ion pair formed (W) is constant [99].
The total number of energy of the incident particle, which is converted into the information carriers, is seen to fluctuate. An empirical constant known as Fano factor is multiplied with the predicted variance to convert it into the experimentally observed variance. The empirical constant is only significant when the detector is operated in pulse mode [100, 101].
The incident particle having sufficient energy ionizes the gas inside the chamber and creates positive ion and free electron. In course of time, the electron and the positive ion gain thermal energy and can diffuse away from the regions of higher density. During thermal motion, collision between positive ion and free electron results in recombination, and a state of charge neutrality exists. However, in presence of electric field, the free electron and positive ion gain momentum, which is known as drift velocity [102]. The drifting of the charges actually constitutes an electric current, and a dc ion chamber is used to measure the ionizing current.
At high voltage, the ionization current will be saturated, the electric field will be large everywhere, and the recombination will be negligible. The percent by which the measured ion current falls short of true saturation is seen to increase as a function of the measured ion current. It is not unusual to observe some imbalance in the steady-state concentrations of the two charges when electron drifts toward anode followed by the drift of positive charge toward cathode. As a result, a gradient will exist for a species that is free to migrate, and some net diffusion must take place in the direction of decreasing concentration. The direction of diffusion will be opposite to the direction of charge carrier flow by the electric field, and the effect will reduce the measured ion current. The ratio of the change in ionizing current to the total ionizing current can be modeled after Rossi and Staub as [103]
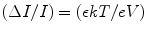
where ϵ is the ratio of the average energy of charge carrier with electric field present to that without electric field, k is Boltzmann constant, T is temperature in absolute, e is electronic charge, and V is the applied voltage.
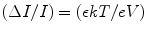
(2.5)
2.10.2 Free-Air Ionization Chamber
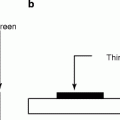
The free–air ionization chamber has become the most popular instrument to measure ionization of gamma rays [104–106]. The parallel plate electrodes inside the chamber receive the collimated gamma (γ)-ray radiation. There are three small electrodes on the top. The central electrode on the top receives the signal, and it is kept at negative potential with respect to the bottom electrode. The two other small electrodes on the top are grounded. Figure 2.14 shows the schematic of a free-air ionization chamber.
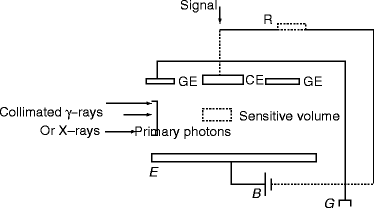

Fig. 2.14
The schematic of a free-air ionization chamber. B battery, G ground, GE guard electrode, CE central electrode, R resistance
The drawback of this system is the loss of ionization due to the creation of secondary electrons at high energy (>100 keV) which creates some difficulties during measurements. In order to minimize the loss of ionization measurements, gamma-ray (γ) energy is kept below 100 keV. At higher energies, γ-ray exposure measurements are carried out in cavity chambers surrounded by a small volume of air. The secondary electrons created by collisions make the surrounding volume of air large. To improve the situation, the volume of air is compressed, and the walls are made sufficiently thick—a condition called electronic equilibrium is established. It has been observed that the exposure rate R (C/kg-s) of an air equivalent ion chamber is directly proportional to the saturated ion current (I s) in amps and inversely proportional to the mass (m) in kilogram (kg), and the relation can be expressed mathematically as
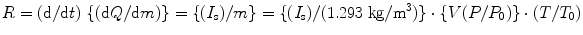
where Q is the charge due to ionization, V is chamber volume (m3), P = air pressure in the chamber, P 0 is the saturated pressure (760 mmHg), T air temperature inside the chamber, and T 0 is standard temperature (273.15 K).
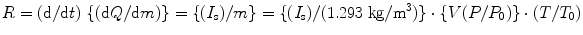
(2.6)
Again, Q, the ionization charge, is equal to (eT)/(W), where e is the electronic charge; T is the kinetic energy of the charged particle; and W is the mean energy required to create an ion pair in a gas. Now, we will introduce a new term called kerma (ℜ), which is defined as the kinetic energy released per unit mass, and we will define it as
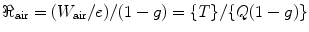
where (1 − g) is the mean correction for energy given to the radiated photon. The value of W air = 33.97 eV with a relative standard uncertainty of 0.15 % [107].
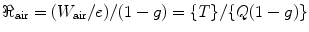
(2.7)
Mostly, the ionization chambers are used in current mode, and the average rate of ion formation within the chamber is measured. However, an ionization chamber can also be operated in pulse mode in which separate radiation quantum gives rise to distinguishable single pulse. The equivalent circuit of an ion chamber operated in pulse mode is shown in Fig. 2.15.
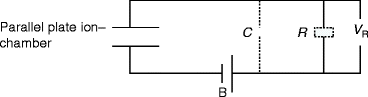

Fig. 2.15
The schematic of the equivalent circuit of an ion chamber operated in pulse mode. C capacitance, R resistance, B battery/external power, V R output voltage
2.10.3 Proportional Counter (PC)
Proportional counter is a gas-filled (mostly 90 % argon and 10 % methane) ionization counter that works on the same principle as the Geiger–Muller (GM) counter. One of the most important applications of PCs as detection and spectroscopic instruments is for low-energy radiation measurements (α-counting, β-counting, mixed α- and β-counting, and for the measurements of γ- and X-rays). They are widely used to detect neutrons. Figure 2.16 shows an earlier version (1952) of a 4-pi gas flow proportional counter. Schutmeister and Meyer are generally credited for the construction of the first true 4-pi detectors in 1947–1948.


Fig. 2.16
An earlier version (1952) of a 4-pi gas flow proportional counter (Photo credit of Oak Ridge Associated Universities)
According to the design, the PC can be position–sensitive, parallel–plate avalanche, multi–wire proportional, or gas proportional scintillation type. It relies on the phenomenon of gas multiplication due to secondary ionization, which is a consequence of increasing electric field, and acceleration of the electron liberated by the secondary ionization process. During its subsequent drift, it undergoes collisions with other neutral gas molecules and creates additional ionization. However, positive and negative ions achieve very little energy between collisions and do not take part in secondary ionization.
Figure 2.17 shows the schematic of a simplified proportional counter circuit, which operates in the proportional region. The circuit illustrates that the walls act as one of the electrodes (cathode) and a long fine wire at the center of the chamber acts as an another electrode (anode). The geometry of the electrodes and the voltage on them are chosen in such a way that in most of the volume of the counter, the electric field strength is not enough to produce a Townsend avalanche [108].
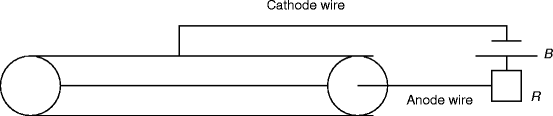

Fig. 2.17
The schematic of a simplified proportional counter circuit. B is the battery, and R is the load resistance
The gas multiplication process takes the form of a cascade and is known as Townsend avalanche (Fig. 2.18). Now, we can define the Townsend avalanche coefficient (α) as the fractional increase in the number of electrons (n) per unit path length (x). Mathematically, it is expressed as
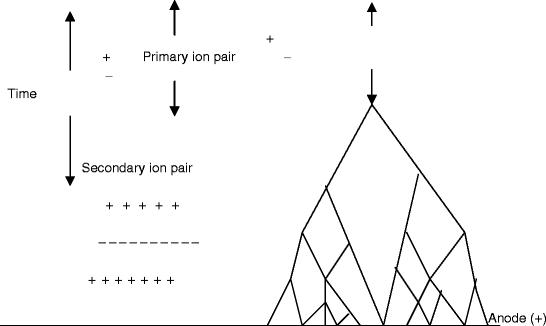
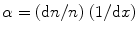

Fig. 2.18
The schematic shows that the primary charged ion pair produces many secondary ion pairs
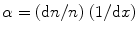
(2.8)
As the applied voltage is increased, a nonlinearity in the pulse form is noticed. On the other hand, when the applied voltage is low, the field is insufficient to prevent recombination of the original ion pairs. However, over some region of the voltage–pulse amplitude curve, gas multiplication is linear, which means that the collected charges are proportional to the original numbers of ion pairs created by the incident radiation. This is the true proportionality region and represents the mode of operation of conventional proportional counter. Assuming the linearity between the Townsend coefficient (α) and the electric field (E), the multiplication factor (M) can be written as
![$$ M=[\{V/(c/a)\}]\cdot [\{\ln\;2/(\Delta V)\}]\;[\{\ln\;(V)\}/\{(\mathrm{ pa}\;\ln\;(b/a)\}-\ln\;K\}] $$](/wp-content/uploads/2017/03/A308734_1_En_2_Chapter_Equ00029.gif)
where K is constant, b = cathode radius, a = anode radius, V = applied voltage, and p = gas pressure [109].
![$$ M=[\{V/(c/a)\}]\cdot [\{\ln\;2/(\Delta V)\}]\;[\{\ln\;(V)\}/\{(\mathrm{ pa}\;\ln\;(b/a)\}-\ln\;K\}] $$](/wp-content/uploads/2017/03/A308734_1_En_2_Chapter_Equ00029.gif)
(2.9)
The charge, which is developed in a pulse during measurement (assuming no nonlinearity), is proportional to the number of ion pairs created (n 0) by the incident radiation. The amplitude of the pulse, however, is seen to fluctuate from pulse to pulse, and the expression for variance in amplitude of the pulse is (Qq/Q)2 and can be written as
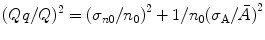
where 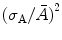 is the single-electron multiplication variation and (σ n0/n 0)2 is the ion pair fluctuation. Following Furry distribution and assuming that A is reasonably large, the expected distribution in the number of electrons produced in a given avalanche reduces to a simple exponential form as
is the single-electron multiplication variation and (σ n0/n 0)2 is the ion pair fluctuation. Following Furry distribution and assuming that A is reasonably large, the expected distribution in the number of electrons produced in a given avalanche reduces to a simple exponential form as
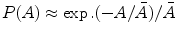
when the multiplication factor A (the mean value of A) is large due to electric field E, (σ A/A)2 ≈ 1/(1 + θ) ≈ c, where θ is a parameter related to the fraction of electrons where energy exceeds a threshold energy for ionization (0 < θ < 1) and c is cathode radius [60].
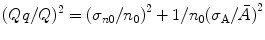
(2.10)
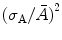 is the single-electron multiplication variation and (σ n0/n 0)2 is the ion pair fluctuation. Following Furry distribution and assuming that A is reasonably large, the expected distribution in the number of electrons produced in a given avalanche reduces to a simple exponential form as
is the single-electron multiplication variation and (σ n0/n 0)2 is the ion pair fluctuation. Following Furry distribution and assuming that A is reasonably large, the expected distribution in the number of electrons produced in a given avalanche reduces to a simple exponential form as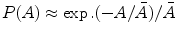
(2.11)
By proper functional arrangement, modifications, and biasing, proportional counter can be used as spectroscopic instruments for soft X-rays and gamma (γ) rays. It can also be used for neutron radiation detection in mixed radiation fields. As a matter of fact, low-energy X-ray spectroscopy is one of the most important applications of proportional counter. The energy of the absorbed photoelectrons formed by photon interaction within the gas is directly related to X-ray energy. However, proportional counter is not used when the gamma rays are having higher photon energies.
2.10.4 Position-Sensitive Proportional Counter
Position–sensitive proportional counter (PSPC) is based on the principle of charge division. The anode is a high-resistive wire and is connected to two amplifiers at two ends. Electrons drift along radial field lines from their place of formation. The position of the avalanche is a good indicator of the axial position at which the original pair is formed. By summing the amplitude of the two amplifiers, a conventional output pulse is produced with amplitude proportional to the total charge (Q A + Q B). A position signal is generated by dividing the output signal of a single amplifier by summed signal {(Q A)/(Q A + Q B)} to give a pulse that will indicate relative position along length.
Figure 2.19 shows the diagram of position localization in proportional counters using charge division {(Q A)/(Q A + Q B)}. It is proportional to the position of the particle track. In the Fig. 2.19, HV is the high voltage and G is the ground. The input impedance I imp of the amplifiers is made high, compared to the resistance of the anode wire, R [61], which is made sufficiently large so that the collected charge on one side divided by the total charge on the two opposite sides of the amplifiers follows a simple relation to the position of the interaction [37, 62, 63]. An alternative method is developed on the basis of the relative rise time from the preamplifiers placed at either end of the resistive wire [64].
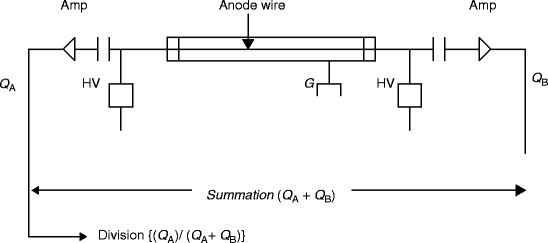

Fig. 2.19
The diagram of position localization in proportional counters using charge division
2.10.5 Parallel-Plate Avalanche Counter
It consists of two parallel plate electrodes separated by a distance inside a closed chamber with a low-pressure gas inside. When a high voltage is applied, a charge particle that traverses the gap between the plates is multiplied through the usual gas amplification process and leaves a trail of ions and electrons. The numbers of ions that are formed and traveled through the gap reflect the amount of energy lost by the particle in transit. Experimental observation shows that for gaps of the order of 1 mm, the fast component rise time is about 2 ns under high field [65].
2.10.6 Geiger–Muller (GM) Counter
It is an instrument that can detect a single particle of ionizing radiation with an operating voltage in the Geiger plateau. It consists of a tube filled with low-pressure (0.1 atm) inert gas and an organic vapor or a halogen gas. Inside the chamber, there are two electrodes, between which a potential difference of several hundred volts is created without any flow of current. Figure 2.20 shows the schematic of an experimental setup with a Geiger–Muller counter.
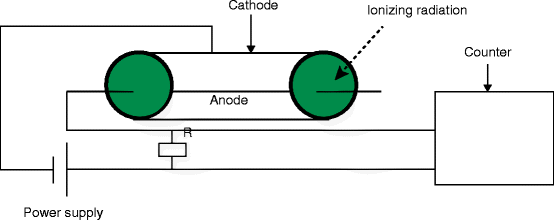

Fig. 2.20
The experimental setup with a Geiger–Muller counter (R resistor)
The electrons from the gas discharge are collected as pulses within a microsecond. The pulses should have two slopes, the fast one corresponding to the collection of electrons and the slower one will correspond the drifting time of the positive ions. A single ion pair formed within the fill gas of the GM tube can trigger a full Geiger discharge, and the counting efficiency can reach 100 %.
A portable GM meter used to survey gamma (γ) radiation consists of high-voltage supply and pulse-counting meter. The higher field in GM tubes enhances the intensity of avalanche process. The most important achievement of a GM counter is that all pulses from a GM tube are of the same amplitude regardless of the number of original ion pairs that initiated avalanche process. Therefore, a GM tube cannot be used for direct radiation spectroscopy rather than as a simple counter of radiation-induced events [66]. Another disadvantage of GM tube is that besides lack of energy information, it has a large dead time that limits its application as radiation detector. Figure 2.21 shows a picture of a Geiger–Muller (GM) counter with an attached probe head.