Radiobiology of Stereotactic Radiosurgery

2
Radiobiology of Stereotactic Radiosurgery

John C. Flickinger

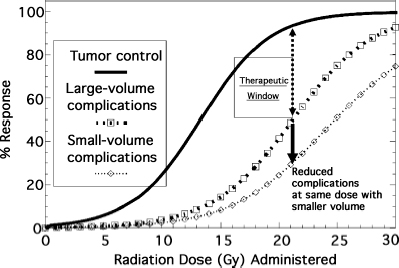
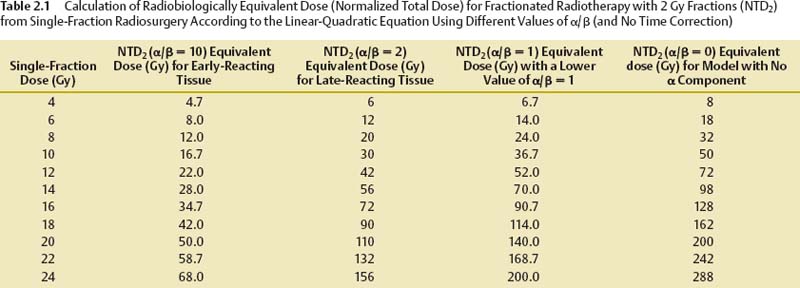
Radiosurgery exploits the ability of small volumes of a normal organ to tolerate much higher radiation doses without injury than large volumes of the same organ. This dose–volume effect for radiation becomes highly pronounced at very small volumes like those treated in radiosurgery. By using stereotactic fixation and localization techniques, radiosurgery allows clinicians to do away with the need to expand radiation treatment volumes by adding margins around well-defined target/tumor volumes to correct for the localization/targeting errors seen with conventional radiotherapy setups. The highly conformal radiation dose distributions delivered through multiple beams using radiosurgery techniques reduce the amount of normal tissue treated to full treatment doses within the intracranial treatment volume and also reduce radiation dose fall-off into surrounding normal tissue outside the target volume. This allows clinicians to change from treating with multiple small dose fractions to total doses that large volumes of surrounding normal tissue can tolerate to treating with high-dose single-fraction radiation doses that markedly smaller, thin rims of normal tissue adjacent to radiosurgical targets can tolerate.

Rationale for Fractionation in Conventional Radiotherapy

Prior to the introduction of radiosurgery, almost all clinical radiation therapy to intracranial targets was fractionated Starting with observation of the reaction of skin that received much higher doses with external beam orthovoltage radiotherapy used before the introduction of megavoltage radiotherapy sources (cobalt 60 and linear particle accelerator [linac]), it became obvious that early and late normal tissue reactions could be limited through fractionation while maintaining high response rates in treating malignant tumors. Radiobiological analysis of a few cell culture lines of fast-growing malignant tumors and analysis of clinical experience of tumor control and complications with some common fast-growing malignant tumors commonly treated with fractionated radiotherapy in the clinic strongly supported this observation. These studies showed that increased fractionation (reducing daily radiation dose fractions to the range of 1.8 to 2.0 Gy per fraction and treating with more fractions to equal or slightly higher total doses) preferentially spared normal tissue from radiation injury without changing tumor control as much. With widespread use of 1.8 to 2.0 Gy fractions, radiation oncologists became most comfortable treating everything that way (both rapidly growing malignant and slow-growing benign tumors), especially because most information about normal tissue tolerance was learned using these fractionation schemes.

Slow-growing benign tumors have been notoriously difficult to study in cell culture or animal models. Their radiobiological responses, particularly how a response changes with different fractionations, are poorly defined. Prior to the advent of radiosurgery, few radiation oncologists had more than limited experience with treating with high doses of single-fraction radiation. Stereotactic radiosurgery provided clinicians the ability to administer high single doses of radiation to intracranial targets with relative safety. Radiosurgery ushered in a new era of understanding of how different approaches to radiation treatment planning and radiobiology may be modified in the clinic to achieve goals previously thought unreachable.

The Mechanics of Tissue Irradiation

When a person undergoes x-ray treatment or cobalt irradiation, the target region is exposed to a high-energy photon beam. That beam interacts with the tissue at the target, producing a cascade of ionizing electrons that in turn cause biochemical damage within the cells exposed to the radiation. Both single- and double-stranded deoxyribonucleic acid (DNA) breaks may occur. Depending on how much biochemical damage occurs and how much of that damage can be repaired by the cell, the consequences lead to necrosis (rapid cell death), apoptosis (slow programmed cell death), or cell survival (with or without survival of abilities such as further mitosis and hormonal secretion). The exact biology of these injury and repair responses is being unraveled to show increasing complexity with potential points of modification.1–3 Tumor control by radiation treatment comes not only through radiation directly affecting tumor cells, but also through effects on the adventitia, most notably the supporting vasculature.⁴ Within the range of doses commonly used for radiosurgery, the dominant mode of cell death in tumors seems to be mediated through radiation effects on endothelial cells in the supporting vasculature.⁴ Pathological studies of tumors resected after radiosurgery also indicate that vascular endothelium may be the primary target responding to radiosurgery.⁵ This vasculature effect seems to explain why single-fraction radiosurgery provides similarly high tumor rates for very different tumors found to differ widely by being either highly resistant or highly sensitive to radiation either in cell culture models or in clinical experience with conventional fractionated radiotherapy.

Optimizing the outcome of any clinical intervention (radiation, drug therapy, or surgery) usually requires striking a balance between maximizing the desired outcome from the intervention (tumor cure, vascular malformation obliteration, etc.) while minimizing undesired sequelae of the intervention (complications). This balance can be represented in many clinical situations by a pair of dose–response curves representing cure (tumor control or arteriovenous malformation [AVM] obliteration) and complications (radiation injury), as shown in Fig. 2.1. The separation between the curves has been referred to as the therapeutic window, and the ratio of cure to complication risk is referred to as the therapeutic ratio. Radiosurgery exploits the radiobiological fact that smaller volumes of normal tissue can withstand much higher doses of radiation than larger volumes of normal tissue. Reducing the volume of tissue irradiated to high doses lessens the complication risk for any dose given to the target, shifting the complication dose–response curve for the treatment to the right, farther away from the complication curve, thereby improving the therapeutic ratio. The effect on both curves must be adequately assessed to evaluate potential radiation dose–response modifications (e.g., altered fractionation, radiation protectors, or radiosensitizing drugs, including some chemotherapy and hypoxic radiation sensitizers) to find if they improve the therapeutic ratio.

Fig. 2.1 Typical sigmoid dose–response curves for tumor control and complications and the effect of reducing treatment volume on the complication curve.

Estimating the Effects of Fractionating Radiation in Radiosurgery

The linear-quadratic formula is the most widely accepted way to represent fractionation effects in radiotherapy.6–11 It relates the log of surviving cells after a dose fraction of ionizing radiation as being proportional to a linear function of the dose per fraction (consisting of the dose per fraction multiplied by a coefficient, α) plus a second quadratic function (consisting of the dose per fraction squared multiplied by a second coefficient, β). This formula forms a power series modeling radiation cell killing with a combination of linear, single-hit kinetics (which could mathematically represent double-stranded DNA breaks leading to cell death) and quadratic, double-hit kinetics (which could mathematically represent a critical accumulation of single-stranded DNA breaks leading to cell death). The linear-quadratic formula represents the probability of either tumor cure or normal tissue injury, P (cure or complication), from a single fraction of radiation of dose, d, by the following probabilistic double-exponential equation:

P(cure or complication) = exp[−K × exp(−α × d − β × d²)] (1)

where exp represents the number e (2.7183, used in natural logarithms) raised exponentially to the power of the terms that follow, K represents the number of target clonogens, and α and β are the linear and quadratic coefficients.

This mathematical expression describes sigmoid-shaped dose–response curves with the probability of cure or complications increasing with dose from 0% to a limit of 100% as dose is increased (Fig. 2.1). Although used in research, this expression of the linear-quadratic formula is virtually never used in day-to-day clinical radiotherapy practice.

A much more useful calculation in the clinic is the formula to equate the effect of a fractionated course of radiotherapy with one dose per fraction (fr) d₁ and total dose D₁ to a different fractionation scheme with dose per fraction d₂ and total dose D₂ according to a given α/β ratio, as follows:

Total dose D₁ Gy × (d₁ Gy/fr + a/b) = total dose − (D₂ Gy × d₂ Gy/fr + α/β) (2)

Another formula useful in the clinic is the expression for NTD_2, the normalized total dose at 2 Gy per fraction, which is the equivalent total dose administered with daily 2 Gy fractions using a given α/β value.6 NTD₂ for a given α/β ratio can be calculated for a course of radiotherapy given with a dose per fraction of d Gy/fr with the following equation:

NTD₂ for (α/β) = total dose at d Gy/fr × (d Gy/fr + α/β)/(2 Gy/fr + α/β) (3)

Table 2.1 shows the 2 Gy/fraction equivalent doses predicted for different single-fraction radiosurgery doses with the linear-quadratic formula using different α/β ratios.

Table 2.1, Eq. 2, and Eq. 3 ignore the effect of overall treatment time, which should be negligible for central nervous system tissue and benign tumors in normal circumstances. A time-dependent repopulation term should be added for protracted fractionated treatment of fast-growing malignant tumors. Repopulation of malignant tumors accelerates 2 to 3 weeks after the start of radiotherapy. Because of clinical studies that related poor tumor control from head and neck cancer radiotherapy with increasing overall treatment time, split-course radiotherapy with planned 2-week breaks in the middle to alleviate mucositis are no longer routinely used.

The ratio of the α coefficient divided by the β coefficient (the α/β ratio) provides a useful parameter to quantify fractionation effects in target tissues and tumors. With the α/β ratio for a given organ or tumor, we can estimate the total dose and number of fractions needed to change from treatment with one dose per fraction to another dose per fraction and with the same effect on that tissue or tumor. Because different kinds of tumors, different organs, and even different types of injury reactions in the same organ (e.g., skin redness vs late skin fibrosis) have different α/β ratios, changing to a different fractionation scheme with an equivalent effect calculated for one organ will lead to a different effect on organs or tumors with different α/β ratios. This became apparent when early radiation therapists tried to switch to cheaper and more convenient hypofractionated radiation schemes with larger dose fractions producing similar acute skin reactions and found increased late complications.

Different tissues can be lumped into categories by their α/β ratios as either early-responding tissues (fast growing with injury responses, e.g., mucositis and skin erythema, occurring a relatively short time after radiation) or late-responding tissues (slow-growing tissues that take a longer time after radiation exposure for injury reactions to become apparent). Studies of fractionation effects in radiotherapy clinics and in animal models found the brain and spinal cord to be late-responding tissues, relatively more sensitive to large-dose fractions, with α/β ratios around 2. Faster growing, faster responding tissues such as skin erythema and mucositis reactions have α/β values in the intermediate range of 5 to 8, whereas many fast-growing malignant tumors have α/β values closer to 10.⁶ Smaller radiation dose fraction schedules cause proportionally less injury to normal tissues (or a limited number of tumors) with a low α/β ratio (a smaller α or single-hit component to radiation cell-kill kinetics) compared with malignant tumors (or faster responding tissues) with higher α/β ratios.

Because most malignant tumors have a higher α/β ratio than adjacent normal tissue, increasing fractionation for conventional large-field radiotherapy improves the therapeutic window most of the time. This is not the case for all tumors that can be treated by radiation and may not hold for radiosurgery dose distributions. First of all, there is a wide variation of α/β ratios found in malignant tumors. Some malignant tumors, such as melanoma and prostate cancer (or at least some strains of them), have lower α/β ratios than surrounding normal tissues (skin or rectum/bladder), supporting the use of larger dose fractions for treatment.¹⁰

Only gold members can continue reading. Log In or Register to continue