or larger), the on-the-shelf depth acquisition devices typically provide lower resolution (e.g.  ) maps. Moreover, in order to reduce the bandwidth occupancy of 3D or multi-view video systems, depth maps are usually downsampled before compression, so that a suitable upsampling stage is needed at receiver side.
) maps. Moreover, in order to reduce the bandwidth occupancy of 3D or multi-view video systems, depth maps are usually downsampled before compression, so that a suitable upsampling stage is needed at receiver side.
Depth maps upsampling techniques recently debated in technical literature involve statistical, possibly Markovian, priors [24, 25], as well as video sequence analysis [37, 38]. In Wang et al. [37, 38], the depth map interpolation method exploits the existing pairs of key frames and their corresponding depth maps. The method requires frame selection, motion alignment, and updating and adjusting of the map. In Lee and Ho [21] the authors generate multi-view video sequences and their corresponding depth maps by making use of a multi-camera system enriched by one time-of-flight depth camera. An initial virtual depth map is generated at each viewpoint, and then the depth map edges are adapted to the estimated moving object edges. The work in [22, 23] deals with adaptive edge-preserving depth map smoothing, which counteracts typical depth based image rendering artifacts, ie holes on the generated virtual view images. In Zhu [42],method for combining the results from both active and passive techniques is built on the base of a pixel-wise reliability function computed for each acquisition method. In Jaesik et al. [19] high quality upsampling uses an additional edge-weighted nonlocal means filtering to regularize depth maps in order to maintain fine detail and structure. The depth image upsampling method in [16] exploits a novel edge layer concept and encompasses it in the design of a non-linear interpolation filter for depth map up-sampling. Edge preserving upsampling for depth map coding purposes appears in [26]. In Tseng and Lai [35], the depth map for all pixels at each frame is estimated by first applying correspondence search, computing the optical flow between selected scenes, and then refining the results by MRF. A depth map post processing scheme for FVT applications appears in [3]. In Xu et al. [40] the depth map preprocessing method using texture edge information to refine depth pixels around the large depth discontinuities. The method in [31] uses edge information from the video frame in the upscaling process and allows the use of sparse, non-uniformly distributed depth values. The method in Rong et al. [28] addresses sharpening edges of the depth maps possibliy degraded by coding. In Vijayanagar et al. [36] a post-processing technique corrects and sharpens the boundaries of the objects of the depth map and ensures local depth smoothness within the objects. The work in De Silva et al. [11] exploits the depth perception sensitivity of humans in suppressing the unnecessary spatial depth details, hence reducing the transmission overhead allocated to depth maps. In Ekmekcioglu [12] an edge adaptive depth map upsampling procedure stemming from an edge map of the original natural image has been proposed. The resulting upsampled depth maps exhibit an increased sharpness in edge regions with respect to classical upsampling such as bilinear interpolation and linear spatial scalable filters [33]. Since no information about the orientation of the edges is considered, some edges still exhibits visual artifacts which, in turn, may severely affect all of the stages where a correct high resolution depth map is required, such as, for instance, the rendering of free viewpoint images. Moreover, the work in Ekmekcioglu [12] estimates the edge map from the high resolution luminance map, thus needing the samples of the low resolution depth map to be correctly registered with the sample of the high resolution luminance map. This latter operation is computationally onerous; besides, it may affect the upsampling procedure when not perfectly performed (Table 1).
4 On the Adoption of MRF Model for Depth Map Interpolation
Depth maps are made up by homogeneous regions separated by abrupt boundaries. In this respect, MRFs, aiming to assign higher probabilities to configurations in which small differences between the pixel values occur in large regions, are well suited to be used as a statistical prior for depth maps. We model the unknown high resolution depth image as a realization of a bidimensional MRF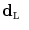 defined on a rectangular lattice
defined on a rectangular lattice 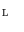 .
.
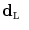 defined on a rectangular lattice
defined on a rectangular lattice 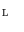 .
.Such model has been successfully applied to natural image upsampling [7], where the model proved to be attractive under different points of view, namely (i) tightness, (ii) availability of low computational cost procedures, (iii) straightforward parameter tuning.
Let us then assume that the depth values are observed on a sub-lattice 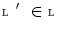 : the observations’ set is then given by
: the observations’ set is then given by 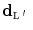 . Here, we address the problem of interpolating the HR depth map
. Here, we address the problem of interpolating the HR depth map 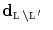 from the observed LR samples, namely
from the observed LR samples, namely 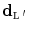 , and we resort to the Maximum a Posteriori (MAP) estimation of the high-resolution samples
, and we resort to the Maximum a Posteriori (MAP) estimation of the high-resolution samples 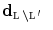 given the observations
given the observations 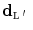 . The analytical expression of the estimator is a particular form of the estimators derived in [7] and it is inherently related to the depth map Markovian prior.
. The analytical expression of the estimator is a particular form of the estimators derived in [7] and it is inherently related to the depth map Markovian prior.
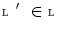 : the observations’ set is then given by
: the observations’ set is then given by 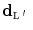 . Here, we address the problem of interpolating the HR depth map
. Here, we address the problem of interpolating the HR depth map 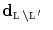 from the observed LR samples, namely
from the observed LR samples, namely 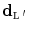 , and we resort to the Maximum a Posteriori (MAP) estimation of the high-resolution samples
, and we resort to the Maximum a Posteriori (MAP) estimation of the high-resolution samples 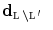 given the observations
given the observations 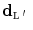 . The analytical expression of the estimator is a particular form of the estimators derived in [7] and it is inherently related to the depth map Markovian prior.
. The analytical expression of the estimator is a particular form of the estimators derived in [7] and it is inherently related to the depth map Markovian prior.Let 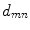 be the value of the random field
be the value of the random field 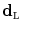 at the pixel
at the pixel 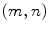 and let
and let 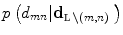 denote the probability density function (pdf) of
denote the probability density function (pdf) of 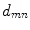 conditioned to the values
conditioned to the values 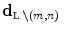 . The random field
. The random field 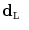 is said to be a MRF if, for every pixel
is said to be a MRF if, for every pixel 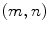 , a neighborhood
, a neighborhood 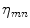 is found such that:
is found such that:
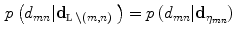
A set of pixels such that all the pixels belonging to the set are neighbors of each other is called a clique. The joint pdf of a random field satisfying (1) takes the form of a Gibbs distribution [15], given by:
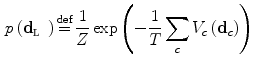
where the functions 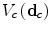 operate on subsets of pixels
operate on subsets of pixels 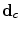 belonging to the same clique
belonging to the same clique 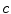 , and the sum is carried out on all the cliques in the field. In this work we will consider cliques composed by two pixels, i.e.
, and the sum is carried out on all the cliques in the field. In this work we will consider cliques composed by two pixels, i.e. 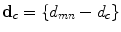 . The functions
. The functions 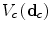 are called potential functions and the parameter
are called potential functions and the parameter 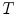 driving the pdfcurvature is often referred to as the temperature of the distribution.
driving the pdfcurvature is often referred to as the temperature of the distribution.
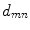 be the value of the random field
be the value of the random field 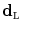 at the pixel
at the pixel 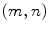 and let
and let 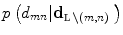 denote the probability density function (pdf) of
denote the probability density function (pdf) of 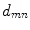 conditioned to the values
conditioned to the values 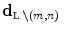 . The random field
. The random field 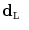 is said to be a MRF if, for every pixel
is said to be a MRF if, for every pixel 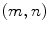 , a neighborhood
, a neighborhood 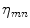 is found such that:
is found such that: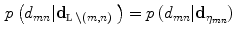
(1)
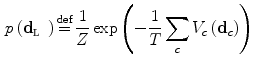
(2)
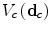 operate on subsets of pixels
operate on subsets of pixels 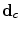 belonging to the same clique
belonging to the same clique 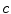 , and the sum is carried out on all the cliques in the field. In this work we will consider cliques composed by two pixels, i.e.
, and the sum is carried out on all the cliques in the field. In this work we will consider cliques composed by two pixels, i.e. 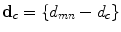 . The functions
. The functions 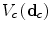 are called potential functions and the parameter
are called potential functions and the parameter 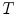 driving the pdfcurvature is often referred to as the temperature of the distribution.
driving the pdfcurvature is often referred to as the temperature of the distribution.The MRF is characterized by the neighborhood system defined on 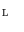 and by the form of the potential functions
and by the form of the potential functions 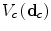 , which ultimately determine the energy, and hence the probability, of the configuration
, which ultimately determine the energy, and hence the probability, of the configuration 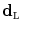 .
.
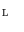 and by the form of the potential functions
and by the form of the potential functions 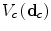 , which ultimately determine the energy, and hence the probability, of the configuration
, which ultimately determine the energy, and hence the probability, of the configuration 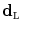 .
. The neighborhood system 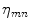 and the potential functions
and the potential functions 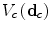 , representing the spatial continuity constraints, definetely identify the MRF. One of the most commonly adopted neighborhood system
, representing the spatial continuity constraints, definetely identify the MRF. One of the most commonly adopted neighborhood system 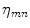 is depicted in Fig. 2. The system, formerly introduced in [15], encompasses only two pixels cliques
is depicted in Fig. 2. The system, formerly introduced in [15], encompasses only two pixels cliques 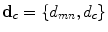 oriented along different directions
oriented along different directions 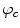 allowing the clique potential
allowing the clique potential 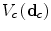 to adapt to up to 8 different edge directions. A commonly assumed form for the potential function
to adapt to up to 8 different edge directions. A commonly assumed form for the potential function 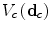 is the parabolyc form:
is the parabolyc form:
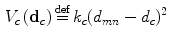
The quadratic term in (3) measures the contribution to the overall configuration energy related to the variations between the pixels 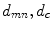 . The term is to be interpreted as follows: high values of
. The term is to be interpreted as follows: high values of 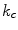 lead to low values of the mass probability for the field configurations presenting abrupt variations along the direction
lead to low values of the mass probability for the field configurations presenting abrupt variations along the direction 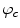 of the clique
of the clique 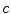 . Meanwhile, small values of
. Meanwhile, small values of 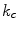 make the overall configuration probability independent on the same variations, and result in looser spatial continuity constraints. Thereby, the weights
make the overall configuration probability independent on the same variations, and result in looser spatial continuity constraints. Thereby, the weights 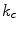 definitely associate higher probabilities to configurations in which small differences between the pixel values occur in large regions.
definitely associate higher probabilities to configurations in which small differences between the pixel values occur in large regions.
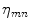 and the potential functions
and the potential functions 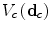 , representing the spatial continuity constraints, definetely identify the MRF. One of the most commonly adopted neighborhood system
, representing the spatial continuity constraints, definetely identify the MRF. One of the most commonly adopted neighborhood system 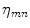 is depicted in Fig. 2. The system, formerly introduced in [15], encompasses only two pixels cliques
is depicted in Fig. 2. The system, formerly introduced in [15], encompasses only two pixels cliques 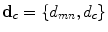 oriented along different directions
oriented along different directions 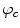 allowing the clique potential
allowing the clique potential 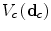 to adapt to up to 8 different edge directions. A commonly assumed form for the potential function
to adapt to up to 8 different edge directions. A commonly assumed form for the potential function 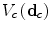 is the parabolyc form:
is the parabolyc form: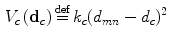
(3)
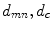 . The term is to be interpreted as follows: high values of
. The term is to be interpreted as follows: high values of 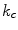 lead to low values of the mass probability for the field configurations presenting abrupt variations along the direction
lead to low values of the mass probability for the field configurations presenting abrupt variations along the direction 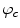 of the clique
of the clique 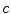 . Meanwhile, small values of
. Meanwhile, small values of 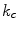 make the overall configuration probability independent on the same variations, and result in looser spatial continuity constraints. Thereby, the weights
make the overall configuration probability independent on the same variations, and result in looser spatial continuity constraints. Thereby, the weights 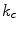 definitely associate higher probabilities to configurations in which small differences between the pixel values occur in large regions.
definitely associate higher probabilities to configurations in which small differences between the pixel values occur in large regions.On regions boundaries, discontinuities are allowed through the use of suitably defined line process, across which the spatial continuity constraints are relaxed. Uniform region boundaries have been modeled by means of suitable binary [15] or real valued [2] line processes. Recently, these models have been generalized by resorting to a complex valued line process [7], which formally takes into account visually relevant characteristics such as the edge intensity and orientation. In Colonnese et al. [7




Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree