Riemannian Framework for Intrinsic Comparison of Closed Genus-Zero Shapes

[14], as well as surface embeddings [15, 16] and diffusion tensors [12]. Reference [17] applies the large deformation framework to compute distances between surfaces as the length of the path in the space of diffeomorphism resulting from morphing one boundary onto another. An improvement on this is suggested in [15], measuring distances on the deformation of the surface itself rather than in the ambient space as done in [17]. Closer still to our work here, Kurtek et al. [16] developed a Riemannian framework for surfaces of spherical topology, using “q-map” representation. The 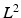$L^{2}$ distance on q-maps, or simply the surface embedding locally weighted by the square root of the volume form, is shown to be invariant under spherical automorphisms. From this, a definition of a path length is developed, encapsulating the degree of spatial deformation between surfaces up to rotation and spherical remapping of one surface over the other. A path-straightening algorithm explicitly parameterized in time is then implemented, allowing both geodesic computation and interpolation. The beauty of this Riemannian approach lies in the ability to directly reconstruct the surface from the representation, which is not found in the surface-based methods discussed above. However, the representation is still of the surface embedding, with all the resulting nuisances. To overcome this, some standard heuristics are applied to the initial surfaces, namely centering each shape at the origin. Thus, a local change in the surface has a global effect on the representation. More importantly, the approach applies to the space 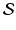${\mathcal{S}}$ of smooth functions from the 2-sphere to 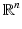${\mathbb{R}}^{n}$ , without any regard for the intrinsic metric structure of the surface. One undesirable effect of this is that the resulting geodesics may enter regions of 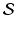${\mathcal{S}}$ corresponding to surfaces with unrealistically severe metric distortion.

Hoping to avoid these confounds, we instead begin with the notion of intrinsic surface representation that is already invariant to nuisance parameters such as Euclidean motion, while capturing the metric structure. Our ultimate goal is a metric space on a complete surface representation. By “complete,” we mean a representation from which a surface can be reconstructed uniquely up to initialization parameters. In general, the ability to reconstruct the object from the representation is not guaranteed, as some of the examples of Riemannian settings above show.

A basic result from surface geometry, the Fundamental Theorem of Surfaces states that a surface can be uniquely represented up to Euclidean motion with two smooth symmetric tensor fields satisfying certain integrability (conditions). With the additional constraint that the first of the tensor fields is positive definite, a surface can be reconstructed given an initial frame. 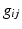The first of these fields is the Riemannian metric tensor on the surface $g_{ij}$ , while the second is the Second Fundamental Form

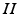, or “shape tensor.” In this work, we mainly focus on the metric tensor. To develop a distance on metric tensors of surfaces, we turn to the work of Ebin [18] and others [19, 20] who have developed a Riemannian framework for the general manifold of metrics tensors. Applying the results to our case – pullback metrics on the 2-sphere induced from the mapped surfaces – we develop a parameterization-invariant comparison of surface metric structures. We show how this measure can be extended to be a metric, when the metric tensor space is restricted to a sub-manifold of fixed-form metrics. Augmenting this distance with metrics on curvatures, we develop a complete representation for surfaces of spherical topology. We apply our method to several brain structures. We show that our method leads to an equiareal mapping between surfaces that is as-conformal-as-possible.

2 A Riemannian Metric on the Space of Metric Tensors

Given an

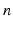-dimensional manifold

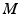, the space of all smooth symmetric tensor fields 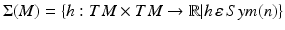$\Sigma (M) = \{ h:TM \times TM \to {\mathbb{R}}|h\,\varepsilon\,Sym(n)\}$ and the subspace of Σ of positive definite tensors 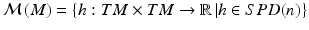${\mathcal{M}}\left( M \right) = \left\{ {h:TM \times TM \to {\mathbb{R}}\left| {h \in SPD(n)} \right.} \right\}$ , our problem above can be restated generally as finding a suitable metric on 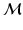${\mathcal{M}}$ , such that the group of diffeomorphisms on

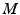acts on 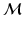${\mathcal{M}}$ by isometry. Ebin et al. [18] showed that the 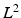$L^{2}$ Riemannian metric on the tangent bundle of 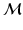${\mathcal{M}}$ , each fiber of which is identified with Σ, indeed satisfies this criteria: given 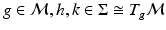$g \in {\mathcal{M}}, h,k \in {\Sigma } \cong T_{g} {\mathcal{M}}$ , the metric can be written as: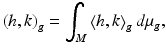

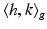$\left( {h,k} \right)_{g} = \int_{M} {\left\langle {h,k} \right\rangle_{g} d\mu_{g},}$

(1)

where $\left\langle {h,k} \right\rangle_{g}$ is the inner product induced by

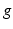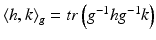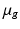, $\left\langle {h,k} \right\rangle_{g} = tr\left( {g^{ - 1} hg^{ - 1} k} \right)$ , and $\mu_{g}$ is the volume form also induced by

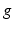. This metric produces geodesics on 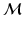${\mathcal{M}}$ whose length can be computed point-wise and in closed form. In other words, a geodesic on 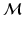${\mathcal{M}}$ is a one-parameter family of metrics 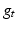$g_{t}$ on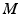

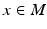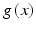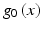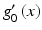, with the tensor at a point $x \in M$ , $g\left( x \right)$ depending only on $g_{0} \left( x \right)$ and $g^{\prime}_{0} \left( x \right)$ . Applying these results to our concrete case, we take

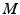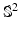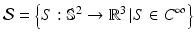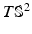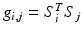to be the 2-sphere ${\mathbb{S}}^{2}$ , and consider the space of metrics pulled back from spherically parameterized surfaces ${\mathcal{S}} = \left\{ {S: {\mathbb{S}}^{2} \to {\mathbb{R}}^{3} \left| {S \in C^{\infty } } \right.} \right\}$ , expressed in canonical coordinates on $T{\mathbb{S}}^{2}$ as $g_{i,j} = S_{i}^{T} S_{j}$ . We illustrate an example of this representation in Fig. 1. A reparameterization 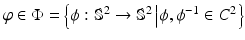$\varphi \in {\Phi } = \left\{ {\phi :{\mathbb{S}}^{2} \to {\mathbb{S}}^{2} \left| {\phi ,\phi^{ - 1} \in C^{2} } \right.} \right\}$ acts on

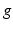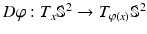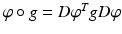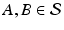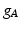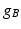by conjugation with the pushforward (Jacobian) $D\varphi :T_{x} {\mathbb{S}}^{2} \to T_{\varphi \left( x \right)} {\mathbb{S}}^{2}$ , $\varphi \circ g = D\varphi^{T} g D\varphi$ . Given two parameterized surfaces $A,B \in {\mathcal{S}}$ , a closed-form solution for the geodesic distance between $g_{A}$ and $g_{B}$ at a point

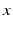is [21]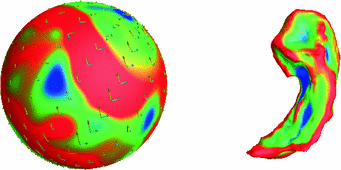

Fig. 1.

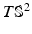Metric tensor fields and mean curvature – a nearly complete surface representation. Tensors are displayed as their eigenvectors in $T{\mathbb{S}}^{2}$ with magnitude corresponding to the eigenvalues. If Gaussian curvature (not shown) is also known, the information on the left is sufficient to reconstruct the hippocampal surface on the right.

$D\left( {g_{A} \left[ x \right],g_{B} \left[ x \right]} \right) = \sqrt {\int_{0}^{1} {\left\langle {g^{\prime}_{t} \left( x \right),g^{\prime}_{t} \left( x \right)} \right\rangle }_{{g_{t\left( x \right)} }} dt} = \left\| {{\text{Log}}\left[ {g_{A}^{ - 1/2} g_{B} g_{A}^{ - 1/2} } \right]} \right\|_{F} .$

(2)

This metric is indeed invariant under simultaneous spherical re-mappings of

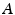and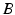

, since 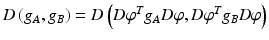$D\left( {g_{A} ,g_{B} } \right) = D\left( {D\varphi^{T} g_{A} D\varphi ,D\varphi^{T} g_{B} D\varphi } \right)$ . These results are derived in [21].

3 Parameterization-Invariant Metric Tensor Comparison

While the measure above is pointwise-invariant to conjugation, integrating the expression following (1) does not in fact le(ad) to a measure that is invariant. This is due to the changing volume form in (1). As we will see, a trade-off must be made between three desirable properties of a shape comparison measure: 1. Invariance under actions by Φ; 2. Point-wise independence; 3. Metric property. 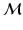Only two of these three properties can be satisfied simultaneously on ${\mathcal{M}}$ . The first of these is crucial for intrinsic shape comparison, for if it fails to hold, the measure is subject to the arbitrary nature of an initial spherical parameterization. The third property can be useful for all the reasons described in the introduction, such as computing intrinsic means and transporting trajectories. The second property is attractive for the ease of computation it implies: the problem reduces to minimizing the integral of the pointwise measures over

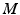. For now, we choose to preserve the first two properties. This requires us to modify the volume form on 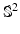${\mathbb{S}}^{2}$ to be symmetric with respect to

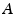and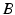

, and independent of the spherical mapping. We define our measure as

$P\left( {A,B} \right) = \mathop \smallint \limits_{{{\mathbb{S}}^{2} }} \left\| {{\text{Log}}\left[ {g_{A}^{ - 1/2} g_{B} g_{A}^{ - 1/2} } \right]} \right\|_{F}^{2} \left[ {det\left( {g_{A} } \right)det\left( {g_{B} } \right)} \right]^{1/4} d{\mathbb{S}}^{2}$

(3)

The volume form $\left[ {det\left( {g_{A} } \right)det\left( {g_{B} } \right)} \right]^{1/4} d{\mathbb{S}}^{2}$ remains unchanged after a re-mapping $\left[ {det\left( {g_{A}^{\varphi } } \right)det\left( {g_{B}^{\varphi } } \right)} \right]^{1/4} df({\mathbb{S}}^{2} ) = \left[ {det\left( {g_{A} } \right)det\left( {g_{B} } \right)} \right]^{1/4} \det \left( {D\varphi } \right)d{\mathbb{S}}^{2} \det \left( {D\varphi^{ - 1} } \right) = \left[ {det\left( {g_{A} } \right)det\left( {g_{B} } \right)} \right]^{1/4} d{\mathbb{S}}^{2}$ . 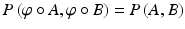Together with the result from the previous section, this shows that $P\left( {\varphi \circ A,\varphi \circ B} \right) = P\left( {A,B} \right)$ . Finding the global minimum of

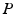by re-parameterizing one surface over the other, we obtain a comparison between the two surfaces’ metric structures that is independent of parameterization and therefore intrinsic: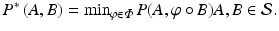

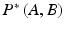$P^{*} \left( {A,B} \right) = \min\nolimits_{\varphi \in \varPhi } P(A,\varphi \circ B) A,B \in {\mathcal{S}}.$

(4)

The measure above is appealing: it leads to a mapping between two surfaces that minimizes metric distortion with a mixture of equiareal and conformal mapping between the surfaces. The minimization reduces to a standard registration problem over spherical automorphisms, with the cost function (3). Further, the mapping between the two surfaces retains its metric-preserving property regardless of the initial spherical mapping: here the sphere is a “dummy space,” only needed as a standard canonical space for computational convenience. However, we cannot say that $P^{*} \left( {A,B} \right)$ is a metric.

4 Metrics on 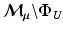${\boldsymbol{\mathcal{M}}}_{\boldsymbol{\mu }} \backslash {\boldsymbol{\Phi}}_{\varvec{U}}$ and on the Space of Surfaces

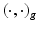The change in the volume form due to reparameterization prevents a straightforward generalization of $\left( { \cdot , \cdot } \right)_{g}$ to the quotient space 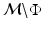${\mathcal{M}}\backslash {\Phi }$ . This is the reason for the breakdown in the metric property of the measure 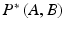$P^{*} \left( {A,B} \right)$ . However, the submanifold 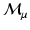${\mathcal{M}}_{\mu }$ of metrics which correspond to a fixed measure 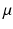$\mu$ admits this generalization. 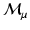${\mathcal{M}}_{\mu }$ is a metric space under 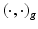$\left( { \cdot , \cdot } \right)_{g}$ , with the geodesic distance defined as usual: 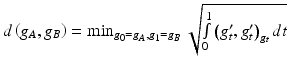$d\left( {g_{A} ,g_{B} } \right) = \min_{{g_{0} = g_{A} ,g_{1} = g_{B} }} \sqrt {\mathop \smallint \limits_{0}^{1} \left( {g^{\prime}_{t} ,g^{\prime}_{t} } \right)_{{g_{t} }} dt}$ . Taking its quotient by the appropriate restriction of Φ to maps with a unitary pushforward 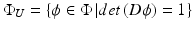${\Phi }_{U} = \left\{ {\phi \in {\Phi }\left| {det\left( {D\phi } \right) = 1} \right.} \right\}$ , we see that 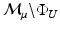${\mathcal{M}}_{\mu } \backslash {\Phi }_{U}$ is also a metric space under the related metric

$d^{*} \left( {g_{A} ,g_{B} } \right) = \mathop {\hbox{min} }\limits_{{ \phi_{t} \in \left\{ {\varphi_{t} :\left[ {0,1} \right] \to {\Phi }_{U} } \right\}}} d\left( {g_{A} ,\phi_{t} \circ g_{B} } \right) = \mathop {\hbox{min} }\limits_{{\begin{array}{*{20}c} {g_{0} = g_{A} ,g_{1} = g_{B} } \\ { \phi_{t} \in \left\{ {\varphi_{t} :\left[ {0,1} \right] \to {\Phi }_{U} } \right\}} \\ \end{array} }} \sqrt {\mathop \smallint \limits_{0}^{1} \left( {g_{t}^{\prime} \left( {\phi_{t} } \right),g_{t}^{\prime} \left( {\phi_{t} } \right) } \right)_{{g_{t} }} dt}$

(5)

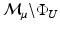Further, it is known that ${\mathcal{M}}_{\mu } \backslash {\Phi }_{U}$ is geodesically complete [19], i.e. the exponential map is defined on the entire tangent space. In particular, this means that geodesic shooting is possible following transport of any velocity between any pair of points on 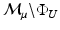${\mathcal{M}}_{\mu } \backslash {\Phi }_{U}$ . The obvious choice for a concrete example of 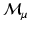${\mathcal{M}}_{\mu }$ is the set of metrics arising from area-preserving spherical maps, i.e. 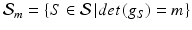${\mathcal{S}}_{m} = \left\{ {S \in {\mathcal{S}}\left| {det\left( {g_{S} } \right) = m} \right.} \right\}$ for some constant

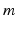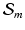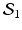. Ensuring scale invariance, we further restrict ${\mathcal{S}}_{m}$ to ${\mathcal{S}}_{1}$ by rescaling surfaces to have area $4\pi$ .

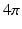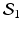Restricting the space of allowable parameterizations to ${\mathcal{S}}_{1}$ may seem like a high price to pay for the ability to use the Riemannian machinery. Yet, it is least restrictive among the three standard parameterizations: conformal, Tuette and equiareal. The genus-zero conformal mapping, for example, only has six degrees of freedom, while the Tuette energy has a unique minimum [1]. The registration arising from this restriction is an equiareal mapping that is as-conformal-as-possible. Thus, we can still expect the resulting registration to approximate near-isometric maps, though perhaps not as well as an unconstrained optimization of 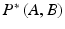$P^{*} \left( {A,B} \right)$ . 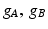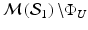A generic path between two points $g_{A },\, g_{B }$ on ${\mathcal{M}}\left( {{\mathcal{S}}_{1} } \right)\backslash {\Phi }_{U}$ may be parameterized at a point on 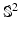${\mathbb{S}}^{2}$ using a family of diffeomorphisms $\phi_{t} \in \left\{ {\varphi_{t}:\left[ {0,1} \right] \to {\Phi }_{U} } \right\}$ as

$g_{t} \left( {\phi_{t} } \right) = g_{A}^{1/2} e^{{t{\text{Log}}\left[ {g_{A}^{ - 1/2} D\phi_{t}^{T} \left( {\phi_{t} \circ g_{B } } \right)D\phi_{t} g_{A}^{ - 1/2} } \right]}} g_{A}^{1/2} .$

The velocity takes the form

$g_{t}^{\prime} \left( {\phi_{t} } \right) = g_{A}^{1/2} \left( {\mathop \smallint \limits_{0}^{1} e^{\alpha tS\left( t \right)} \left[ {S\left( t \right) + tS^{\prime}\left( t \right)} \right]e^{{\left( {1 - \alpha } \right)tS\left( t \right)}} d\alpha } \right)g_{A}^{1/2} ,$