(the signed distance function) as a level set 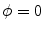 [16]. The evolution of the level set function
[16]. The evolution of the level set function 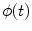 is governed by
is governed by 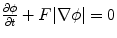 , where
, where 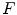 is the speed function. Based on the variational framework, an energy function
is the speed function. Based on the variational framework, an energy function 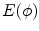 is defined in relation to the the speed function. The minimization of such energy generates the Euler-Lagrange equation, and the evolution of the equation is through calculus of variation:
is defined in relation to the the speed function. The minimization of such energy generates the Euler-Lagrange equation, and the evolution of the equation is through calculus of variation:
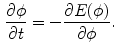
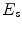 and an edge-mounted Willmore energy
and an edge-mounted Willmore energy 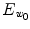 is employed:
is employed: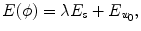
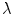
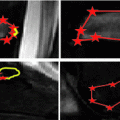
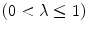 is the weight parameter, which is tuned to suit the segmentation of normal and abnormal spinal vertebrae.
is the weight parameter, which is tuned to suit the segmentation of normal and abnormal spinal vertebrae.2.1 Computing Prior Shape Energy via Kernel Density Estimation
Kernel density estimation (KDE) is a nonparametric approach for estimating the probability density function of a random variable. Without assuming the prior shapes are Gaussian distributed, KDE presents advantage in estimating the shape distribution even with a small number of training set, in addition to modeling shapes with high complexity and structure. In this study, we adopted the prior shape energy formulation discussed by Cremers et al. [2].
The density estimation is formulated as a sum of Gaussian of shape dissimilarity measures 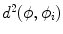 ,
, 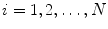 :
:
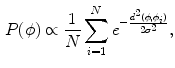 where the shape dissimilarity measure
where the shape dissimilarity measure 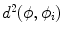 is defined as
is defined as
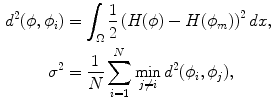 and
and 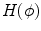 is the Heaviside function. By maximizing the conditional probability
is the Heaviside function. By maximizing the conditional probability
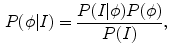 and considering the shape energy as
and considering the shape energy as
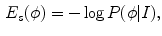 the variational with respect to
the variational with respect to 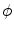 becomes
becomes
![$$\begin{aligned} \frac{\partial E_s}{\partial \phi }=&\frac{\sum _{i=1}^N \alpha _i \frac{\partial }{\partial \phi } d^2(\phi , \phi _i)}{2\sigma ^2 \sum _{i=1}^N \alpha _i}\\ =&\sum _{i=1}^N \frac{e^{-\frac{d^2(\phi , \phi _i)}{2\sigma ^2}}}{2\sigma ^2 \sum _{i=1}^N \alpha _i} \Bigg ( 2\delta (\phi ) \bigg [H(\phi )-H(\phi _i(x-\mu _\phi ))\bigg ]\\&\quad + \int \bigg [H(\phi (\xi )-H(\phi _i(\xi -\mu _\phi ))\bigg ] \delta \phi (\xi ) \frac{(x-\mu _\phi )^T\nabla \phi (\xi ) }{\int H\phi dx} d\xi \Bigg ), \end{aligned}$$](/wp-content/uploads/2016/03/A323246_1_En_3_Chapter_Equ7.gif) where
where 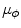 is the centroid of
is the centroid of 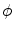 and
and 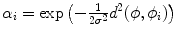 is the weight factor for
is the weight factor for 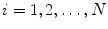 .
.
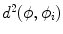 ,
, 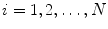 :
: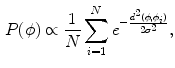
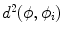 is defined as
is defined as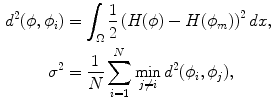
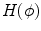 is the Heaviside function. By maximizing the conditional probability
is the Heaviside function. By maximizing the conditional probability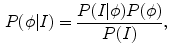
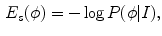
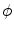 becomes
becomes![$$\begin{aligned} \frac{\partial E_s}{\partial \phi }=&\frac{\sum _{i=1}^N \alpha _i \frac{\partial }{\partial \phi } d^2(\phi , \phi _i)}{2\sigma ^2 \sum _{i=1}^N \alpha _i}\\ =&\sum _{i=1}^N \frac{e^{-\frac{d^2(\phi , \phi _i)}{2\sigma ^2}}}{2\sigma ^2 \sum _{i=1}^N \alpha _i} \Bigg ( 2\delta (\phi ) \bigg [H(\phi )-H(\phi _i(x-\mu _\phi ))\bigg ]\\&\quad + \int \bigg [H(\phi (\xi )-H(\phi _i(\xi -\mu _\phi ))\bigg ] \delta \phi (\xi ) \frac{(x-\mu _\phi )^T\nabla \phi (\xi ) }{\int H\phi dx} d\xi \Bigg ), \end{aligned}$$](/wp-content/uploads/2016/03/A323246_1_En_3_Chapter_Equ7.gif)
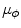 is the centroid of
is the centroid of 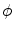 and
and 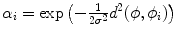 is the weight factor for
is the weight factor for 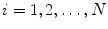 .
.2.2 Computing Local Geometry Energy via Willmore Flow
Willmore energy is a function of mean curvature, which is a quantitative measure of how much a given surface deviates from a sphere. It is formulated as
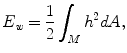 where
where  is a
is a 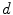 -dimensional surface embedded in
-dimensional surface embedded in 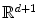 and
and 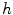 the mean curvature on
the mean curvature on 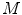 [18]. For image segmentation, the Willmore energy provides an internal energy that gives a useful description of a region, where the effect of edge indicator is not significant. In these regions, smoothness of the shape of the curve should be maintained and extended, which can be regarded as a weak form of inpainting [3].
[18]. For image segmentation, the Willmore energy provides an internal energy that gives a useful description of a region, where the effect of edge indicator is not significant. In these regions, smoothness of the shape of the curve should be maintained and extended, which can be regarded as a weak form of inpainting [3].
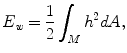
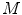 is a
is a 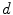 -dimensional surface embedded in
-dimensional surface embedded in 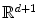 and
and 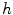 the mean curvature on
the mean curvature on 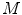 [18]. For image segmentation, the Willmore energy provides an internal energy that gives a useful description of a region, where the effect of edge indicator is not significant. In these regions, smoothness of the shape of the curve should be maintained and extended, which can be regarded as a weak form of inpainting [3].
[18]. For image segmentation, the Willmore energy provides an internal energy that gives a useful description of a region, where the effect of edge indicator is not significant. In these regions, smoothness of the shape of the curve should be maintained and extended, which can be regarded as a weak form of inpainting [3].As a geometric functional, the Willmore energy is defined on the geometric representation of a collection of level sets. Its gradient flow can be well represented by defining a suitable metric, the Frobenius norm, on the space of the level sets. Frobenius norm is a convenient choice as it is equivalent to the 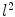 -norm of a matrix and more importantly it is computationally attainable. As Frobenius norm is an inner-product norm, the optimization in the variational method comes naturally.
-norm of a matrix and more importantly it is computationally attainable. As Frobenius norm is an inner-product norm, the optimization in the variational method comes naturally.
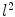 -norm of a matrix and more importantly it is computationally attainable. As Frobenius norm is an inner-product norm, the optimization in the variational method comes naturally.
-norm of a matrix and more importantly it is computationally attainable. As Frobenius norm is an inner-product norm, the optimization in the variational method comes naturally.Based on the formulation by Droske and Rumpf [3], the Willmore flow or the variational form for the Willmore energy with respect to 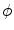 is
is
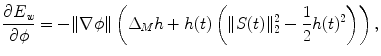 where
where 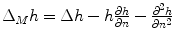 is the Laplacian Beltrami operator on
is the Laplacian Beltrami operator on 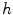 with
with 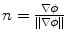 ,
, 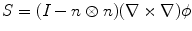 is the shape operator on
is the shape operator on 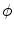 and
and 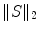 is the Frobenius norm of
is the Frobenius norm of 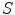 .
.
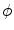 is
is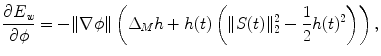
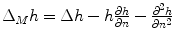 is the Laplacian Beltrami operator on
is the Laplacian Beltrami operator on 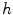 with
with 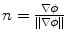 ,
, 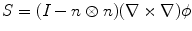 is the shape operator on
is the shape operator on 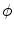 and
and 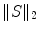 is the Frobenius norm of
is the Frobenius norm of 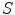 .
.Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree