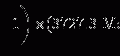(1)
Faculty of Medicine, Department, of Oncology and Medical Physics Unit, McGill University, Montreal, Québec, Canada
Abstract
Chapter 3 consists of 21 problems that cover 4 sections devoted to the Rutherford-Bohr model of the atom that Bohr introduced in 1913. Bohr combined Rutherford’s concept of the nuclear atom with Planck’s idea of quantized nature of the radiation process and developed from first principles an atomic model that successfully deals with one-electron structures, such as the hydrogen atom. The model is based on four postulates that combine classical mechanics with the concept of angular momentum quantization.
The problems of this chapter concentrate on concepts that Bohr enunciated 100 years ago for one-electron structures to predict accurately the radius of electron orbits, velocity of electron in allowed orbit, binding energy of electron while in allowed orbit, as well as photon spectra emitted by excited one-electron atoms. At the end of the chapter, problems also address issues related to multi-electron atoms and experimental confirmation of the Bohr atomic theory.
The set of problems in Sect. 3.1 covers one-electron structures in detail and deals not only with hydrogen but also with other one-electron structures, such as one-electron ions and more exotic Bohr-like atomic structures such as positronium, muonium, antihydrogen, etc. Problems in this group also address the corrections to Bohr theory resulting from the finite mass of the nucleus. Problems of Sect. 3.2 deal with multi-electron atoms and issues related to periodic properties of elements, spectra of characteristic radiation emitted by multi-electron atoms, and the Hartree approximation.
Problems of Sect. 3.3 cover the three experiments that serve as experimental confirmation of Bohr theory: (1) atomic emission and absorption spectra, (2) Moseley experiment on characteristic lines from metallic x-ray targets, and (3) Franck–Hertz experiment. The last question of this chapter deals with the atomic radius calculated using the Schrödinger equation for hydrogen atom (Sect. 3.4).
Chapter 3 consists of 21 problems that cover 4 sections devoted to the Rutherford-Bohr model of the atom that Bohr introduced in 1913. Bohr combined Rutherford’s concept of the nuclear atom with Planck’s idea of quantized nature of the radiation process and developed from first principles an atomic model that successfully deals with one-electron structures, such as the hydrogen atom. The model is based on four postulates that combine classical mechanics with the concept of angular momentum quantization.
The problems of this chapter concentrate on concepts that Bohr enunciated 100 years ago for one-electron structures to predict accurately the radius of electron orbits, velocity of electron in allowed orbit, binding energy of electron while in allowed orbit, as well as photon spectra emitted by excited one-electron atoms. At the end of the chapter, problems also address issues related to multi-electron atoms and experimental confirmation of the Bohr atomic theory.
The set of problems in Sect. 3.1 covers one-electron structures in detail and deals not only with hydrogen but also with other one-electron structures, such as one-electron ions and more exotic Bohr-like atomic structures such as positronium, muonium, antihydrogen, etc. Problems in this group also address the corrections to Bohr theory resulting from the finite mass of the nucleus. Problems of Sect. 3.2 deal with multi-electron atoms and issues related to periodic properties of elements, spectra of characteristic radiation emitted by multi-electron atoms, and the Hartree approximation.
Problems of Sect. 3.3 cover the three experiments that serve as experimental confirmation of Bohr theory: (1) atomic emission and absorption spectra, (2) Moseley experiment on characteristic lines from metallic x-ray targets, and (3) Franck–Hertz experiment. The last question of this chapter deals with the atomic radius calculated using the Schrödinger equation for hydrogen atom (Sect. 3.4).
3.1 Bohr Model of Hydrogen Atom
3.1.Q1 (83)
Larmor classical electromagnetic (EM) theory states that when a charged particle is accelerated or decelerated part of its kinetic energy is emitted in the form of EM radiation (photons). Using classical physics (Larmor law) estimate the time of collapse of the Bohr orbit for hydrogen atom in the ground state.
SOLUTION:
At first glance the Rutherford-Bohr atomic model is analogous to the Kepler-Newton planetary model except that in the latter the Newton gravitational attraction between the sun and the planet plays the role of the centripetal force, while in the former the centripetal force is provided by the Coulomb electrostatic attraction between the positively charged nucleus and the negative electron. However, the difficulty with the Rutherford-Bohr model is that the electron is charged and, by revolving about the nucleus, it is also constantly accelerated. Therefore, by virtue of its charge, the electron should be losing part of its energy in the form of photons and, according to classical physics, spiral into the nucleus.
In Rutherford-Bohr theory of the hydrogen atom the Coulomb force F Coul provides the centripetal force F cent and is expressed as follows
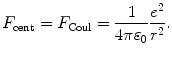
The magnitude of the electron centripetal (radial) acceleration a r and kinetic energy E K, respectively, of the electron are classically given as
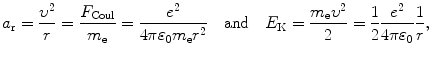
with e,υ, and m e the charge, velocity, and mass of the electron, respectively, ε 0 the electric constant, and r the distance between the electron and the nucleus (proton).
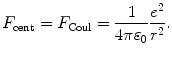
(3.1)
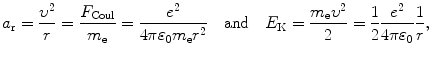
(3.2)
Total energy E of the electron in the ground state of hydrogen is given as (T3.7)
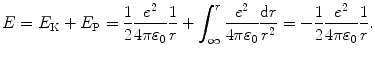
Inserting 1/r from (3.3) into (3.2) yields the following expression for acceleration a
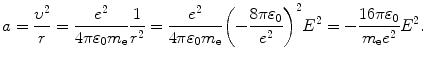
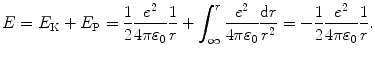
(3.3)
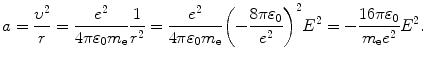
(3.4)
According to the classical Larmor expression (T4.18) the power emitted by an accelerated particle of charge e is given as
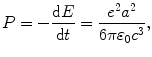
which, after inserting (3.4), reads
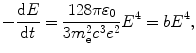
where b is a constant given as
![$$ \begin{aligned}[b] b &= \frac{128\pi \varepsilon _{0}c}{3(m_{\mathrm{e}}c^{2})^{2}e^{2}} = \frac{128\pi {\times} [8.85 {\times} 10^{ - 12}\ \mathrm{A} \cdot \mathrm{s}/(\mathrm{V} \cdot \mathrm{m})] {\times} (3 {\times} 10^{8}\ \mathrm{m}/\mathrm{s})}{3 {\times} (0.511 {\times} 10^{6}\ \mathrm{eV})^{2} {\times} e {\times} (1.6 {\times} 10^{ - 19}\ \mathrm{A} \cdot \mathrm{s})} \\ &= 8.51 {\times} 10^{6}\ (\mathrm{eV})^{ - 3} \cdot \mathrm{s}^{ - 1}. \end{aligned} $$](/wp-content/uploads/2016/04/A212719_1_En_3_Chapter_Equ7.gif)
The differential equation (3.6) will now be rearranged to read
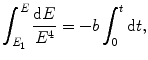
resulting in the following general solution
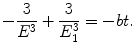
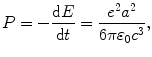
(3.5)
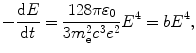
(3.6)
![$$ \begin{aligned}[b] b &= \frac{128\pi \varepsilon _{0}c}{3(m_{\mathrm{e}}c^{2})^{2}e^{2}} = \frac{128\pi {\times} [8.85 {\times} 10^{ - 12}\ \mathrm{A} \cdot \mathrm{s}/(\mathrm{V} \cdot \mathrm{m})] {\times} (3 {\times} 10^{8}\ \mathrm{m}/\mathrm{s})}{3 {\times} (0.511 {\times} 10^{6}\ \mathrm{eV})^{2} {\times} e {\times} (1.6 {\times} 10^{ - 19}\ \mathrm{A} \cdot \mathrm{s})} \\ &= 8.51 {\times} 10^{6}\ (\mathrm{eV})^{ - 3} \cdot \mathrm{s}^{ - 1}. \end{aligned} $$](/wp-content/uploads/2016/04/A212719_1_En_3_Chapter_Equ7.gif)
(3.7)
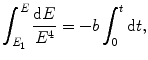
(3.8)
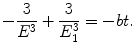
(3.9)
To determine the time of orbit collapse we carry out the integration in (3.8) in energy E from E 1=−13.61 eV (ground state of hydrogen atom) to −∞ (energy level for r→0) and in time t from the initial time (t=0) to the time of orbit collapse at t=t coll. The time of orbit collapse is thus given as
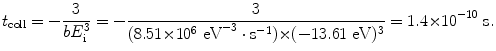
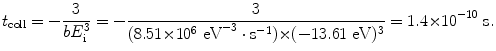
(3.10)
3.1.Q2 (84)
A hypothetical excited one-electron atom (NOT hydrogen) releases a visible photon of wavelength λ=5500 Å. Assume that
Determine:
(1)
Atom follows the Bohr atomic model.
(2)
Nuclear mass is infinitely large in comparison with the mass of the orbital electron.
(3)
Photon originated from an n=3→n=2 (also known as M–L) electronic transition.
(a)
Ionization potential (IP) of this hypothetical atom.
(b)
Energy level diagram (first 5 energy levels) of this hypothetical atom.
(c)
Minimum excitation potential of the hypothetical one-electron atom.
SOLUTION:
Five energy levels in addition to the n=∞ level are plotted in the energy level diagram for the hypothetical excited one-electron atom shown in Fig. 3.1. The ionization potential of the atom is designated by x and the M–L transition is also indicated.
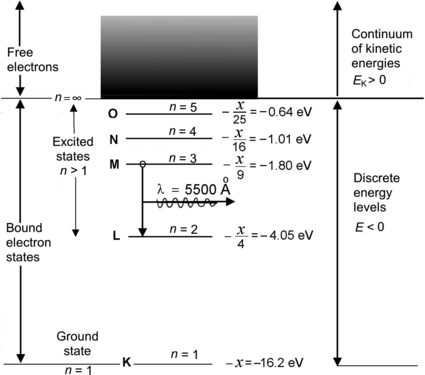

Fig. 3.1
Atomic energy level diagram for the hypothetical one-electron atom of Prob. 84
(a) We first determine the energy hν of the photon emitted with a wavelength λ=5500 Å and get
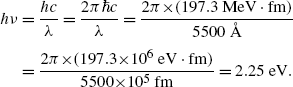
Next, we calculate the ionization potential x by setting the emitted photon energy hν=2.25 eV equal to the difference between energy level M (n=3; energy level =−x/32) and energy level L (n=2; energy level =−x/22) as follows
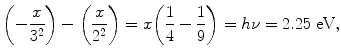
resulting in
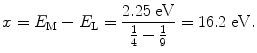
Thus, the ionization potential of our hypothetical one-electron atom is +16.2 eV and the ground state energy level (n=1) is at E(n=1)=E 1=−16.2 eV.
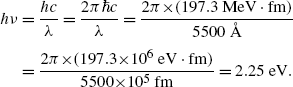
(3.11)
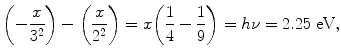
(3.12)
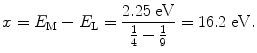
(3.13)
(b) The energy levels for the ground state (n=1) and first four excited states (n>1) of our one-electron hypothetical atom are plotted schematically in Fig. 3.1 and given as follows
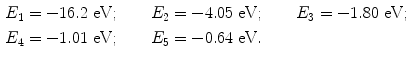 (c) The minimum excitation potential of the hypothetical one-electron atom is the energy required to transfer the orbital electron from the ground state (n=1) to the first excited state (n=2). This energy is equal to |E K−E L|=|−16.2 eV−4.05 eV|=12.15 eV.
(c) The minimum excitation potential of the hypothetical one-electron atom is the energy required to transfer the orbital electron from the ground state (n=1) to the first excited state (n=2). This energy is equal to |E K−E L|=|−16.2 eV−4.05 eV|=12.15 eV.
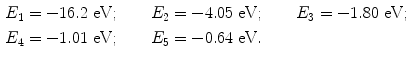
3.1.Q3 (85)
A single-electron ion emits a photon of wavelength λ=1170 Å when its electron makes a transition from the n=4 to the n=3 atomic energy level. Assume that the nuclear mass is infinite in comparison with the electron mass.
(a)
Determine momentum p ν and energy E ν of the emitted photon.
(b)
Determine the atomic number Z of the nucleus.
(c)
Determine the binding energy E B(K) of the electron when it is in the K shell.
(d)
Draw an atomic energy level diagram of the ion for n=1 to n=5 energy levels and indicate the electronic transition from n=4 to n=3.
(e)
Determine the wavelength λ of the photon emitted by the ion when its electron undergoes a transition from the n=5 energy level to ground state. Indicate the electronic transition on diagram plotted in (d).
SOLUTION:
(a) Photon momentum p ν is calculated from the general relativistic expression for total energy E of any particle (including a photon) with rest energy E 0
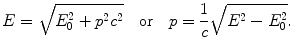
For a photon rest energy E 0=E ν =0 and from (3.14) we get the following expression for the photon momentum
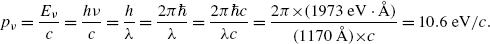
A photon with wavelength λ=1170 Å possesses energy E ν according to Planck law
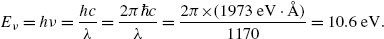
We can obtain the result of (3.16) faster by using the photon momentum p ν of (3.15), since
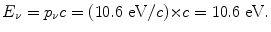
(b) Atomic number Z of the ion will be determined through the following steps:
Looking at the periodic table of elements we find that the element with Z=4 is beryllium. The one-electron ion that we are dealing with in this problem is therefore a triply-ionized beryllium atom Be+++.
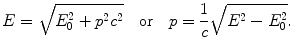
(3.14)
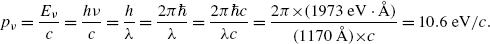
(3.15)
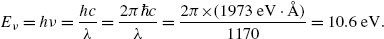
(3.16)
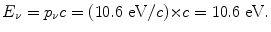
(3.17)
(1)
We know that ΔE 4−3, the energy difference between n=4 and n=3 atomic energy levels is equal to the emitted photon energy E ν =10.6 eV, as determined in (a).
(2)
The n=4 and n=3 atomic energy levels are, respectively, given as
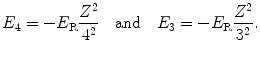
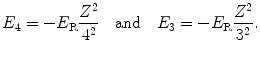
(3.18)
(3)
We thus have
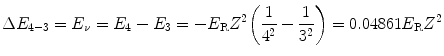
or
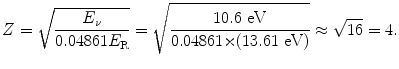
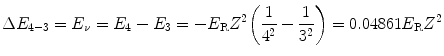
(3.19)
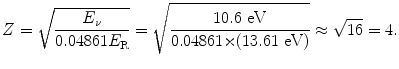
(3.20)
(c) To determine the binding energy E B(K) of the electron in the K shell (also known as the n=1 shell) of Be+++ we now find the energy E 1 of the ground state. Since, in general, the energy levels E n are given by
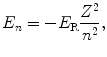
and the ground state energy E 1 is thus given as
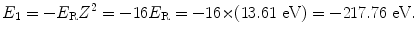
The binding energy E B(K) of the K shell electron in Be+++ ion is thus +217.76 eV. Note: By convention, in contrast to the positive binding energy E B(K), the K shell energy level of Be+++ is negative at E 1=−217.76 eV.
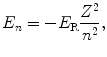
(3.21)
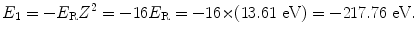
(3.22)
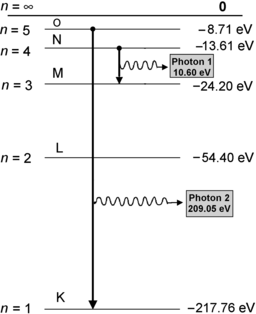
(d) Energy levels for the first five values of n are calculated from (3.22) and plotted in Fig. 3.2
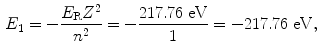
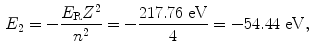
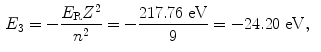
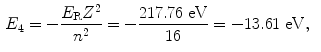
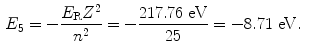
Atomic energy levels for a Be+++ ion from n=1 to n=5 are plotted in Fig. 3.2. Also plotted are electronic transitions (1) from n=4 to n=3 resulting in photon 1 with energy of 10.6 eV and (2) from n=5 to n=1 resulting in photon 2 with energy of 209.05 eV.
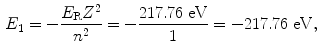
(3.23)
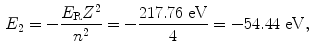
(3.24)
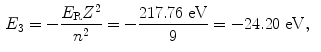
(3.25)
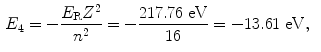
(3.26)
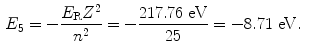
(3.27)

Fig. 3.2
Atomic energy level diagram for one-electron structure Be+++ ion
(e) Energy released in the form of a photon following the n=5 to n=1 electronic transition is
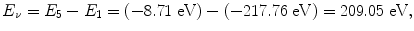
(see Fig. 3.2) corresponding to the following wavelength λ
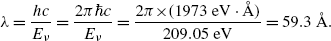
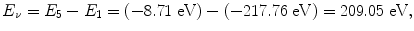
(3.28)
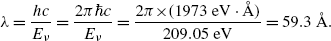
(3.29)
3.1.Q4 (86)
Accounting for the finite size of the nucleus, derive from basic principles the following equations for the Bohr theory of one-electron atoms:
(a)
Angular momentum L n of electron while in orbit with principal quantum number n.
(b)
Kinetic energy E K of the electron–nucleus system.
(c)
Force F e on electron while in orbit n.
(d)
Using results from (a), (b), and (c) determine expressions for radius r n of Bohr orbit n, velocity ν n of electron while in orbit n, and total energy E n of electron while in orbit n.
SOLUTION:
Bohr initially derived his theory of one-electron atoms assuming that nuclear mass M is infinite and that the electron revolves about a point at the center of the nucleus. Experimental studies of hydrogen spectrum have shown a minute discrepancy of the order of one part in 2000 between measured data and theoretical calculations and the discrepancy was attributed to the finite size of the nucleus making both the electron as well as the nucleus to revolve about their common center-of-mass, as shown schematically in Fig. 3.3. In deriving the kinematics of the Bohr atom we thus consider the electron–nucleus system and derive equations of motion for the whole system rather than just for the orbital electron.
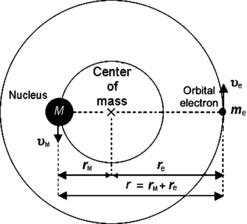

Fig. 3.3
Schematic diagram of the Rutherford–Bohr atomic model with one orbital electron of mass m e and a finite nucleus of mass M. Both the orbital electron and the nucleus revolve about their common center-of-mass
The following relationships will be useful in our calculations
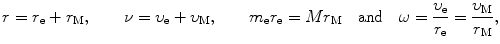
where
We now express r e and r M as follows
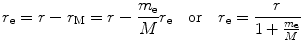
and
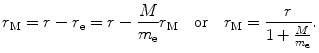
In a similar fashion we express υ e and υ M as
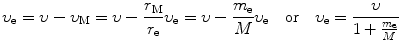
and
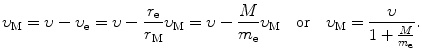
(a) Angular momentum L for our electron-nucleus system is in general given as
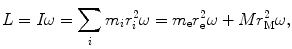
where I is the rotational inertia of the electron–nucleus system given as 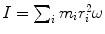 .
.
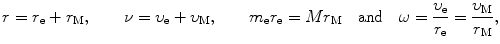
(3.30)
m e and M
are the mass of electron and nucleus, respectively.
r e and r M
are the radius of electron and nucleus orbit, respectively.
υ e and υ M
are the velocity of electron and nucleus, respectively, while in orbit.
ω
is the angular frequency of the electron and nucleus revolving about their common center-of-mass (see Fig. 3.3).
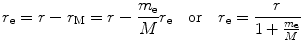
(3.31)
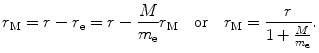
(3.32)
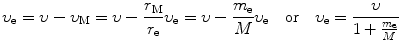
(3.33)
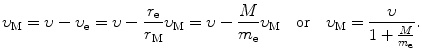
(3.34)
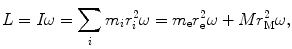
(3.35)
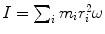 .
.Using expressions for r e and r M given in (3.31) and (3.32), respectively, we now express (3.35) as
![$$\begin{aligned} L &= \frac{m_{\mathrm{e}}r^{2}\omega}{ ( 1 + \frac{m_{\mathrm{e}}}{M} )^{2}} + \frac{Mr^{2}\omega}{ ( 1 + \frac{M}{m_{\mathrm{e}}} )^{2}} = r^{2}\omega \biggl[ \frac{m_{\mathrm{e}}M^{2}}{(m_{\mathrm{e}} + M)} + \frac{m_{\mathrm{e}}^{2}M}{(m_{\mathrm{e}} + M)} \biggr] \\ &= \frac{m_{\mathrm{e}}M}{m_{\mathrm{e}} + M}r^{2} \omega = \mu _{\mathrm{M}}r^{2}\omega, \end{aligned}$$](/wp-content/uploads/2016/04/A212719_1_En_3_Chapter_Equ36.gif)
where μ M is defined as the reduced mass of the electron–nucleus system
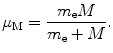
Using the result of (3.36) we now express the angular momentum L as a function of υ and r as
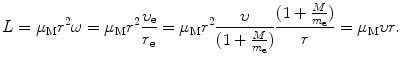
(b) Kinetic energy E K of the electron–nucleus system is given as
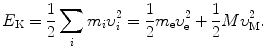
Using expressions for υ e and υ M given in (3.33) and (3.34), respectively, we now express (3.39) as follows
![$$\begin{aligned} E_{\mathrm{K}}& = \frac{1}{2}\frac{m_{\mathrm{e}}\upsilon ^{2}}{ ( 1 + \frac{m_{\mathrm{e}}}{M} )^{2}} + \frac{1}{2} \frac{M\upsilon ^{2}}{ ( 1 + \frac{M}{m_{\mathrm{e}}} )^{2}} = \frac{\upsilon ^{2}}{2} \biggl[ \frac{m_{\mathrm{e}}M^{2}}{(m_{\mathrm{e}} + M)} + \frac{m_{\mathrm{e}}^{2}M}{(m_{\mathrm{e}} + M)} \biggr] \\ &= \frac{1}{2}\frac{m_{\mathrm{e}}M\upsilon ^{2}}{m_{\mathrm{e}} + M} = \frac{1}{2} \mu _{\mathrm{M}}\upsilon ^{2}. \end{aligned}$$](/wp-content/uploads/2016/04/A212719_1_En_3_Chapter_Equ40.gif)
(c) Force F e exerted on the orbital electron is in general given as
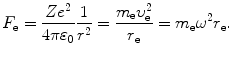
After inserting (3.31) and (3.33) into (3.41) we get the following expression for force F e
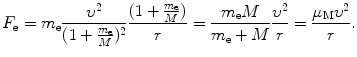
(d) In (a), (b), and (c) we stated all equations that are required in the derivation of Rutherford–Bohr atom kinematics, accounting for the finite mass of the nucleus.
![$$\begin{aligned} L &= \frac{m_{\mathrm{e}}r^{2}\omega}{ ( 1 + \frac{m_{\mathrm{e}}}{M} )^{2}} + \frac{Mr^{2}\omega}{ ( 1 + \frac{M}{m_{\mathrm{e}}} )^{2}} = r^{2}\omega \biggl[ \frac{m_{\mathrm{e}}M^{2}}{(m_{\mathrm{e}} + M)} + \frac{m_{\mathrm{e}}^{2}M}{(m_{\mathrm{e}} + M)} \biggr] \\ &= \frac{m_{\mathrm{e}}M}{m_{\mathrm{e}} + M}r^{2} \omega = \mu _{\mathrm{M}}r^{2}\omega, \end{aligned}$$](/wp-content/uploads/2016/04/A212719_1_En_3_Chapter_Equ36.gif)
(3.36)
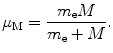
(3.37)
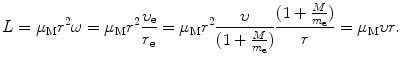
(3.38)
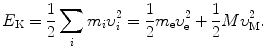
(3.39)
![$$\begin{aligned} E_{\mathrm{K}}& = \frac{1}{2}\frac{m_{\mathrm{e}}\upsilon ^{2}}{ ( 1 + \frac{m_{\mathrm{e}}}{M} )^{2}} + \frac{1}{2} \frac{M\upsilon ^{2}}{ ( 1 + \frac{M}{m_{\mathrm{e}}} )^{2}} = \frac{\upsilon ^{2}}{2} \biggl[ \frac{m_{\mathrm{e}}M^{2}}{(m_{\mathrm{e}} + M)} + \frac{m_{\mathrm{e}}^{2}M}{(m_{\mathrm{e}} + M)} \biggr] \\ &= \frac{1}{2}\frac{m_{\mathrm{e}}M\upsilon ^{2}}{m_{\mathrm{e}} + M} = \frac{1}{2} \mu _{\mathrm{M}}\upsilon ^{2}. \end{aligned}$$](/wp-content/uploads/2016/04/A212719_1_En_3_Chapter_Equ40.gif)
(3.40)
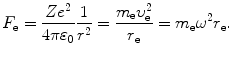
(3.41)
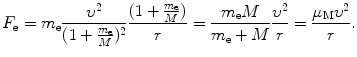
(3.42)
Combining (3.38) with the third Bohr postulate on quantization of angular momentum (L=nħ), we get the following expression for the angular momentum L
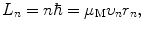
and combining (3.41) with (3.43) we get the following result for the radius of orbit n
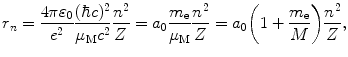
where a 0 is defined as the Bohr radius constant (a 0=0.5292 Å).
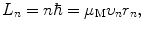
(3.43)
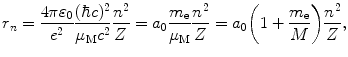
(3.44)
Combining (3.43) with (3.44) results in the following expression for υ n /c
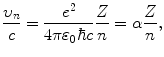
where α is the fine structure constant (α=1/137).
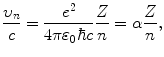
(3.45)
The total energy level of the electron in orbit n is calculated by adding the kinetic energy E K and potential energy E P to get
![$$ \begin{aligned}[b] E_{n} &= E_{\mathrm{K}} + E_{\mathrm{P}} = \frac{1}{2}\mu _{\mathrm{M}}\upsilon _{n}^{2} - \frac{Ze^{2}}{4\pi \varepsilon _{0}}\frac{1}{r_{n}} = - \frac{1}{2} \biggl( \frac{e^{2}}{4\pi \varepsilon _{0}} \biggr)^{2}\frac{(\mu _{\mathrm{M}}c^{2})}{(\hbar c)^{2}} \biggl( \frac{Z}{n} \biggr)^{2} \\ & = - E_{\mathrm{R}}\frac{\mu _{\mathrm{M}}}{m_{\mathrm{e}}} \biggl( \frac{Z}{n} \biggr)^{2} = - E_{\mathrm{R}}\frac{1}{1 + \frac{m_{\mathrm{e}}}{M}} \biggl( \frac{Z}{n} \biggr)^{2}, \end{aligned} $$](/wp-content/uploads/2016/04/A212719_1_En_3_Chapter_Equ46.gif)
where E R is the Rydberg energy constant (E R=13.61 eV).
![$$ \begin{aligned}[b] E_{n} &= E_{\mathrm{K}} + E_{\mathrm{P}} = \frac{1}{2}\mu _{\mathrm{M}}\upsilon _{n}^{2} - \frac{Ze^{2}}{4\pi \varepsilon _{0}}\frac{1}{r_{n}} = - \frac{1}{2} \biggl( \frac{e^{2}}{4\pi \varepsilon _{0}} \biggr)^{2}\frac{(\mu _{\mathrm{M}}c^{2})}{(\hbar c)^{2}} \biggl( \frac{Z}{n} \biggr)^{2} \\ & = - E_{\mathrm{R}}\frac{\mu _{\mathrm{M}}}{m_{\mathrm{e}}} \biggl( \frac{Z}{n} \biggr)^{2} = - E_{\mathrm{R}}\frac{1}{1 + \frac{m_{\mathrm{e}}}{M}} \biggl( \frac{Z}{n} \biggr)^{2}, \end{aligned} $$](/wp-content/uploads/2016/04/A212719_1_En_3_Chapter_Equ46.gif)
(3.46)
Equations for r n (3.44), normalized velocity υ n /c (3.45), and electron energy level E n (3.46) were determined by accounting for the finite nuclear mass, but are similar to those obtained for infinite nuclear mass (T3.3), (T3.5), and (T3.7) except for a correction factor (1+m e/M)=m e/μ M for the radius, no correction factor for velocity, and a correction factor (1+m e/M)−1=μ M/m e for energy level.
3.1.Q5 (87)
For hydrogen atom:
(a)
Compare expressions for orbital radii r n , electron orbital velocities υ n , and atomic energy levels E n calculated assuming an infinite mass of the nucleus (M→∞) to those calculated for a finite nuclear mass M.
(b)
For the three parameters r n ,υ n and E n determine the correction factor f to be applied to expressions for infinite nuclear mass (M→∞) to obtain expressions valid for finite nuclear mass.
(c)
Plot general correction factors of (b) for r n ,υ n , and E n in the range 0≤m/M≤1, where m is the mass of the orbiting particle and M is the mass of the heavier particle.
(d)
Determine and plot on graph (c) correction factors f r,f υ , and f E for (1) muonic hydrogen and (2) positronium. Muonic hydrogen atom consists of a proton p (m p c 2=1836m e c 2) and negative muon μ − (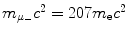 ) and positronium consists of a positron and electron.
) and positronium consists of a positron and electron.
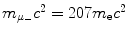 ) and positronium consists of a positron and electron.
) and positronium consists of a positron and electron.SOLUTION:
Table 3.1
Summary of Bohr atom expressions for orbital radius r n , electron orbital velocity υ n , and atomic energy level E n for infinite nuclear mass in column (2), finite nuclear mass in column (3), appropriate constants in column (4), and correction factor in column (5). μ M is the reduced mass of the electron–nucleus system
(1) | (2) | (3) | (4) | (5) |
|---|---|---|---|---|
Infinite nuclear mass M | Finite nuclear mass M | Bohr theory constants | Correction factor | |
Radius r n | 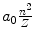 | 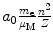 | 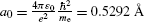 | 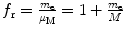 |
Velocity υ n | 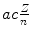 | 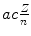 | 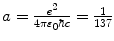 | f υ =1 |
Energy level E n | 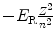 | 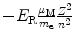 | 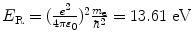 | 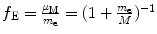 |
(a) Expressions for orbital radii r n , electron orbital velocities υ n , and atomic energy levels E n are derived in (T3.3), (T3.5), and (T3.7), respectively, assuming an infinite nuclear mass and in Prob. 86 accounting for the finite mass of the nucleus. The results are summarized in Table 3.1, columns (1) through (4).
(b) Correction factors to be applied to expressions for infinite nuclear mass (M→∞ column 2 in Table 3.1) to obtain expressions valid for finite nuclear mass (column 3) for the three parameters r n ,υ n , and E n are as follows:
Correction factor f r for orbital radius r n of one-electron Bohr atom is given as
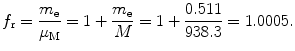
Correction factor f υ for the velocity υ n of orbital electron is equal to 1, i.e., there is no correction for velocity when going from infinite to finite mass considerations.
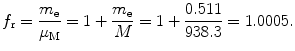
(3.47)
Correction factor f E for energy levels E n of one-electron Bohr atom is
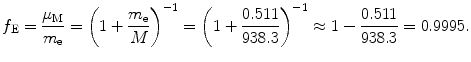
Answers to this section are summarized in Table 3.1, column (5).
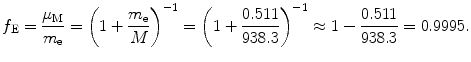
(3.48)
(c) The Bohr theory for hydrogen atom that initially assumed an infinite nuclear mass worked well because the nucleus (proton or deuteron or triton, etc.) exceeds the electron mass by at least a factor of 1836=m p c 2/(m e c 2). For other types of one-electron structures, such as the positronium Ps, muonium Mu, and muonic hydrogen H μ where the two masses are close to one another, one must account for both masses and use the appropriate value for the orbiting particle mass as well as for the reduced mass μ M of the system, as given in column (3) of Table 3.1. The correction factor, presented in column (5) of Table 3.1 can be generalized to all hydrogen-type structures in which one particle with a given charge and mass m revolves around another particle of opposite charge and mass M.
The general correction factor for mass m orbiting around larger mass M thus follows the following rules:
(1)
For radius r n correction factor f r can be generalized to read 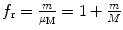 .
.
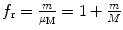 .
.(2)
For velocity υ n correction factor f υ remains equal to 1 irrespective of the ratio m/M.
(3)
For energy levels E n corrections factor f E is 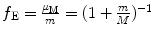 .
.
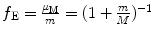 .
.Correction factors f r,f υ , and f E are plotted in Fig. 3.4 in the mass ratio m/M range between 0 and 1.
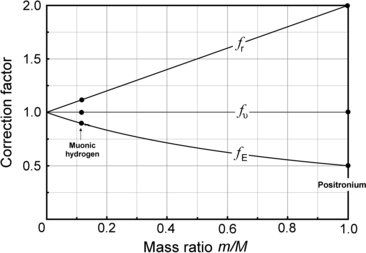

Fig. 3.4
Small mass m and large mass M revolve about a common center-of-mass. General correction factors f r,f υ , and f E to be applied to expressions for radius r, velocity υ, and energy E valid for infinite large mass (M→∞) to obtain expressions valid for finite large mass M
(d) Finite mass correction factors for (1) muonic hydrogen and (2) positronium.
(1)
Muonic hydrogen consists of negative muon (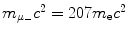 ) and proton revolving about their common center-of-mass in a Bohr atom type configuration (
) and proton revolving about their common center-of-mass in a Bohr atom type configuration (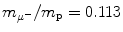 ).
).
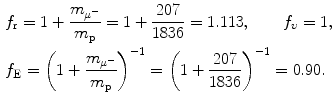
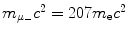 ) and proton revolving about their common center-of-mass in a Bohr atom type configuration (
) and proton revolving about their common center-of-mass in a Bohr atom type configuration (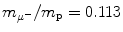 ).
).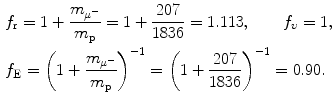
(3.49)
(2)
Positronium consists of positron and electron revolving about their common center-of-mass in a Bohr atom type configuration (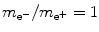 ).
).
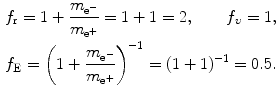
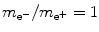 ).
).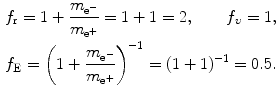
(3.50)
3.1.Q6 (88)
Reduced mass μ M represents an effective mass of a two-body system, consisting of two masses: m and M. Defined as
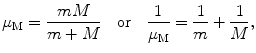
reduced mass μ M of a two-body system has units of mass and is used to simplify a two-body problem into an equivalent one-body problem with effective mass equal to the reduced mass. The reduced mass has many applications in physics and is used in Bohr theory of one-electron atoms to account for the finite mass of the nucleus.
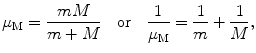
(3.51)
Calculate the reduced mass μ M for the following Bohr-like atomic structures: protium (hydrogen-1), deuterium, tritium, positronium, muonium, antihydrogen, and muonic hydrogen. For each of the seven structures also state its atomic constituents and their mass.
SOLUTION:
Answers to this problem are summarized in Table 3.2.
Table 3.2
Constituents and their reduced mass for the following Bohr-like atomic structures: protium, deuterium, tritium, positronium, muonium, antihydrogen, and muonic hydrogen
Bohr-like structure | Constituents M and m | Mass of constituents | Ratio  | Reduced mass μ M |
|---|---|---|---|---|
Protium H-1 | M: proton p | M=1836m e | 5.45×10−4 | 0.9995m e |
m: electron e − | m=m e | |||
Antihydrogen  | M: antiproton  | M=1836m e | 5.45×10−4 | 0.9995m e |
m: positron e + | m=m e | |||
Deuterium H-2 | M:p+2 neutrons | M=3670.5m e | 2.72×10−4 | 0.9997m e |
m: electron e − | m=m e | |||
Tritium H-3 | M:p+3 neutrons | M=5497m e | 1.82×10−4 | 0.9998m e |
m: electron e − | m=m e | |||
Positronium Ps | M: positron e + | m=m e | 1.0 |